基于过渡圆弧半径求解方法的无人艇循迹控制研究*

韩 鑫 徐海祥 余文曌 周志杰

(高性能船舶技术教育部重点实验室1) 武汉 430063) (武汉理工大学交通学院2) 武汉 430063) (钦州学院机械与船舶海洋工程学院3) 钦州 535099)

0 引 言

无人艇循迹控制是指无人艇在工作或航行过程中，沿着某一条预定的轨迹运动，此过程中要求保持无人艇的艏向沿着预定轨迹.国内外学者已对船舶循迹控制做了大量工作，国外学者Fossen等[1-6]对欠驱船舶的循迹控制做了详细讨论，国内学者聂兵等[7-10]也对循迹控制做了相关研究.

无人艇循迹模式由三部分组成：路径规划、引导系统和控制系统.在路径规划中，路径是由许多路径点组成，其中最典型的连接方式是采用直线和圆弧光滑连接.Fossen[11]在相邻的直线段间加入圆弧过渡，解决了路径的不连续问题，但在经过圆弧时并没有经过中间路径点.文献[7-8]对铺管船的循迹控制进行了研究，通过在每一个路径点处定义一个回转半径，实现直线间的光滑过渡.文献[10]对欠缺船舶循迹控制进行了研究，并通过改进直线和圆弧的路径规划，使船舶经过圆弧时同时经过中间路径点.虽然上述国内外学者都对循迹过程中路径规划做了相关研究，但是迄今为止过渡圆弧的半径值都是人为给定的某一固定值，并没有给出确切的圆弧半径求解方法.而在实际的无人艇循迹控制应用中，如圆弧半径取值过小，会使无人艇舵的性能达不到回转性能要求，造成实际路径与规划路径不吻合；如圆弧半径取值过大，则造成无人艇实际路径与直线连接路径产生较大的偏移.

针对圆弧半径的取值问题，本文对圆弧半径的求解问题进行了研究，提出一种圆弧半径的求解方法.

1 无人艇定常回转运动的受力分析

无人艇作定常回转运动时，回转枢心记做点P，见图1.此时无人艇舵产生的转舵力矩与无人艇受到的阻力矩平衡.

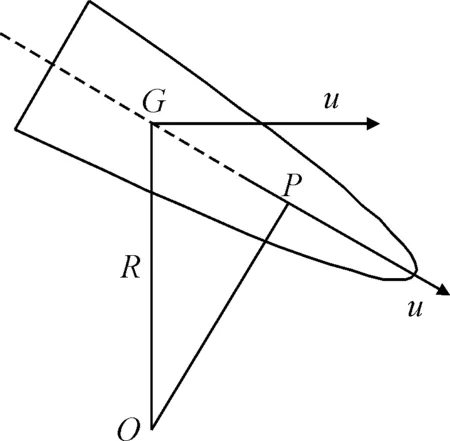
图1 无人艇回转枢心

无人艇在经过中间路径点时需要圆弧过渡，对于主推带舵推进系统的无人艇而言，需要在已知操纵性能的条件下，计算出满舵条件下圆弧的最小曲率半径.最后，通过安全系数来确定无人艇循迹过程中过渡圆弧的半径.

针对无人艇循迹过程中圆弧半径取值问题，本文考虑了环境阻力矩对无人艇回转运动的影响，完善了文献[11]提出的求解无人艇回转半径的方法，使其更加符合无人艇循迹控制的条件.

1.1 无人艇转舵力矩

无人艇舵产生的转舵力矩，可由经验公式计算得出.

ρAu2l

(1)

式中:CL为舵的升力系数;ρ为水的密度;A为舵叶的一侧浸水面积;l为舵杆轴线到无人艇重心的距离.

1.2 静水阻力矩

无人艇在静水中运动时，只需考虑水产生的阻力矩.无人艇作定常回转运动时，绕枢心P匀速转动(见图2)，回转运动过程中，水产生的阻力矩与无人艇的形状与水下纵剖面积有关.假定水下中纵剖面为矩形，此矩形产生的阻力矩即无人艇在静水中回转运动所受的阻力矩.

图2 无人艇中纵剖面

根据文献[11]得出静水对无人艇产生的阻力矩为

(2)

式中：ω为无人艇绕枢心转动的角速度.

1.3 环境阻力矩

无人艇正常工作时，其运动会受到来自风、浪、流等环境载荷的影响，从而影响其回转半径大小.假定无人艇在回转过程中受到的最大环境扰动力矩为bmax，则环境载荷产生的最大阻力矩为

(3)

1.4 曲率半径

假定无人艇在过渡圆弧处做定常回转运动，此时无人艇舵产生的力矩与静水阻力矩和环境阻力矩相平衡，即

Nr+Ms+Me=0

(4)

将式(1)～(3)带入式(4)得

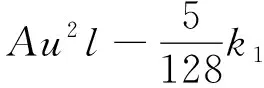
(5)

则角速度ω为

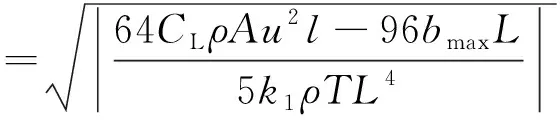
(6)

无人艇作定常回转时，如果其转动角度π,则运动的距离为πR，两者经过的时间相同，即

(7)

将式(6)带入式(7)，考虑安全系数k2(k2>1，取k2=1.5)，得出

(8)

由式(8)可知，无人艇循迹经过中间路径点的圆弧半径R与无人艇及舵的一些基本参数和环境阻力矩有关，这些在仿真过程过程中都是作为已知参数输入,因此，任意无人艇在循迹过程中的圆弧半径R都是通过计算得出的已知量，避免R取值的人为性.

2 无人艇运动数学模型

无人艇在循迹过程中，一般只考虑三个自由度的影响，即纵荡、横荡和艏摇.为了描述无人艇在三自由度的运动情况，建立北东坐标系OE-XEYEZE和船体坐标系O-XYZ，见图3.其中，北东坐标系中原点取海上或陆上任意一点，XE轴指向正北，YE轴指向正东，ZE轴指向地心；船体坐标系中原点取水线面、中纵剖面和中横剖面的交点，X轴指向船首为正，Y轴指向右舷为正，Z轴指向基线为正.

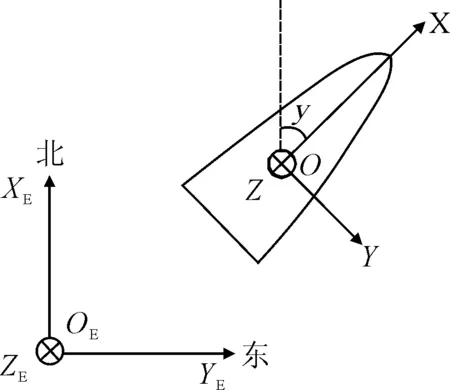
图3 北东坐标系和船体坐标系

根据文献[1]，无人艇三自由度的数学模型为

(9)

式中：M∈R3×3为惯性矩阵；C(ν)∈R3×3为科里奥利向心力矩阵；D(ν)∈R3×3为阻尼系数矩阵；τ∈R3×1为推进器推力；b∈R3×1为作用在无人艇上的环境扰动力；up=[Tp,δ]T为螺旋桨的推力和操舵角组成的向量；Bu∈R3×3为执行机构的配置矩阵；Tu为表征执行机构动态响应速率的定常矩阵；uc=[Tpc,δc]T为控制器的输出；η=(x,y,ψ)T为无人艇在固定坐标系下的位置；ν=(u,υ,r)T为无人艇在船体坐标系下的速度；R(ψ)∈R3×3为坐标转换矩阵.模型中矩阵的具体形式为

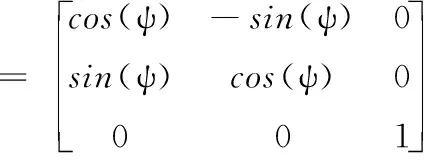
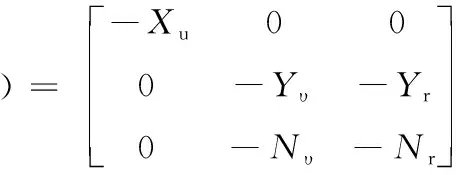
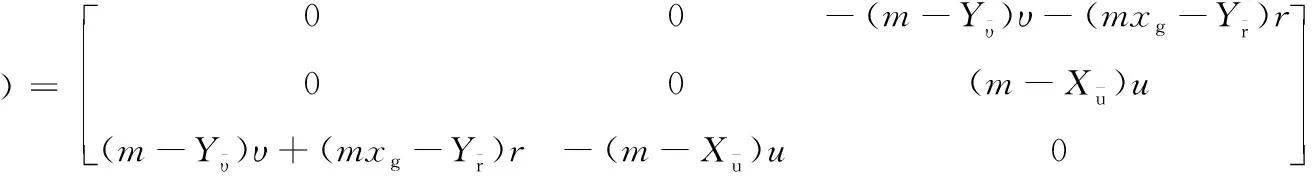
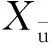
对于主推带舵的无人艇，Bu和up为

式中：t为推力减额分数；Yδ和Nδ为舵的水动力系数.对于欠驱无人艇，控制器输出up表示为

(10)

式中：umax和umin分别为无人艇推进器推力和舵角的最大值和最小值.

3 引导系统和控制器设计

引导系统设计中，本文引入路径平行坐标系(path parallel)的概念，该坐标系的X轴与路径相切，Y轴与X轴成右手坐标系，见图4.

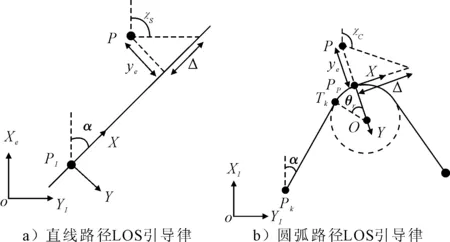
图4 直线和圆弧的LOS引导律

对于直线路径而言，无人艇循迹过程中所需要的艏向角ψd，即为图4a)中所示的引导艏向角χs，χs表示为

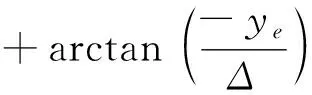
(11)

对于圆弧路径而言，无人艇循迹过程中所需要的艏向角ψd，即为图4b)中所示的引导艏向角χc，χc表示为

(12)

式中：Δ为时变的前向距离；ye为横向偏差.

本文采用文献[10]采用的反步积分控制器，其纵向和艏向控制率：

(13)

4 仿真结果及分析

为了验证圆弧半径求解方法在无人艇循迹过程中的合理性，采用挪威科技大学Cybership 2模型进行无人艇循迹控制仿真，其中模型参数、LOS引导律、控制器和环境力等参数见表1.

无人艇循迹过程中设定五个路径点，坐标值见表2.

根据本文提出的圆弧半径求解方法，得出仿真船模在所设环境条件下的圆弧半径R≈1.2 m，为了验证圆弧半径求解方法的有效性，在控制器参数等条件都相同的前提下，设计两种仿真情况的圆弧半径.①三段圆弧半径均为1.2 m；②三段圆弧的半径分别为0.5，1.2，2 m.

采用line of sight (LOS) 引导律和基于反步积分和Lyapunov理论的非线性控制器对无人艇循迹控制进行仿真，仿真结果见图5～7.

图5为无人艇在两种情况下均达到了循迹控制的效果，由图5a)可知，无人艇在整个循迹过程中实际路径与规划路径吻合的非常好，并且实际路径与直线连接路径也未发生较大偏移；图5b)在圆弧半径R=0.5 m处，无人艇的实际路径与规划路径并不能很好的吻合，造成该结果是因为无人艇舵的性能不足，无法达到规划路径的回转效果；在圆弧半径R=2 m处，虽然无人艇的实际路径与规划路径吻合的非常好，但是实际路径与直线连接路径发生较大的偏移，是因为圆弧半径取值过大造成的.

表1 相关参数

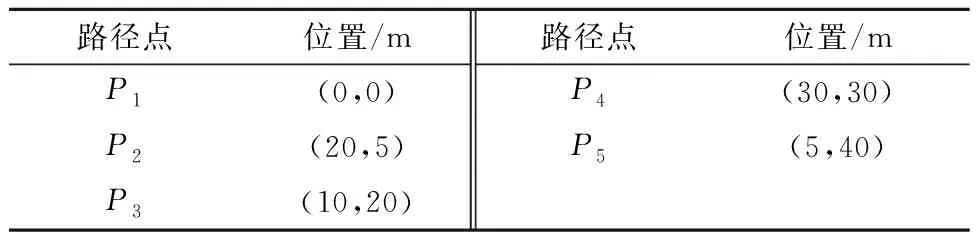
表2 路径点设定值

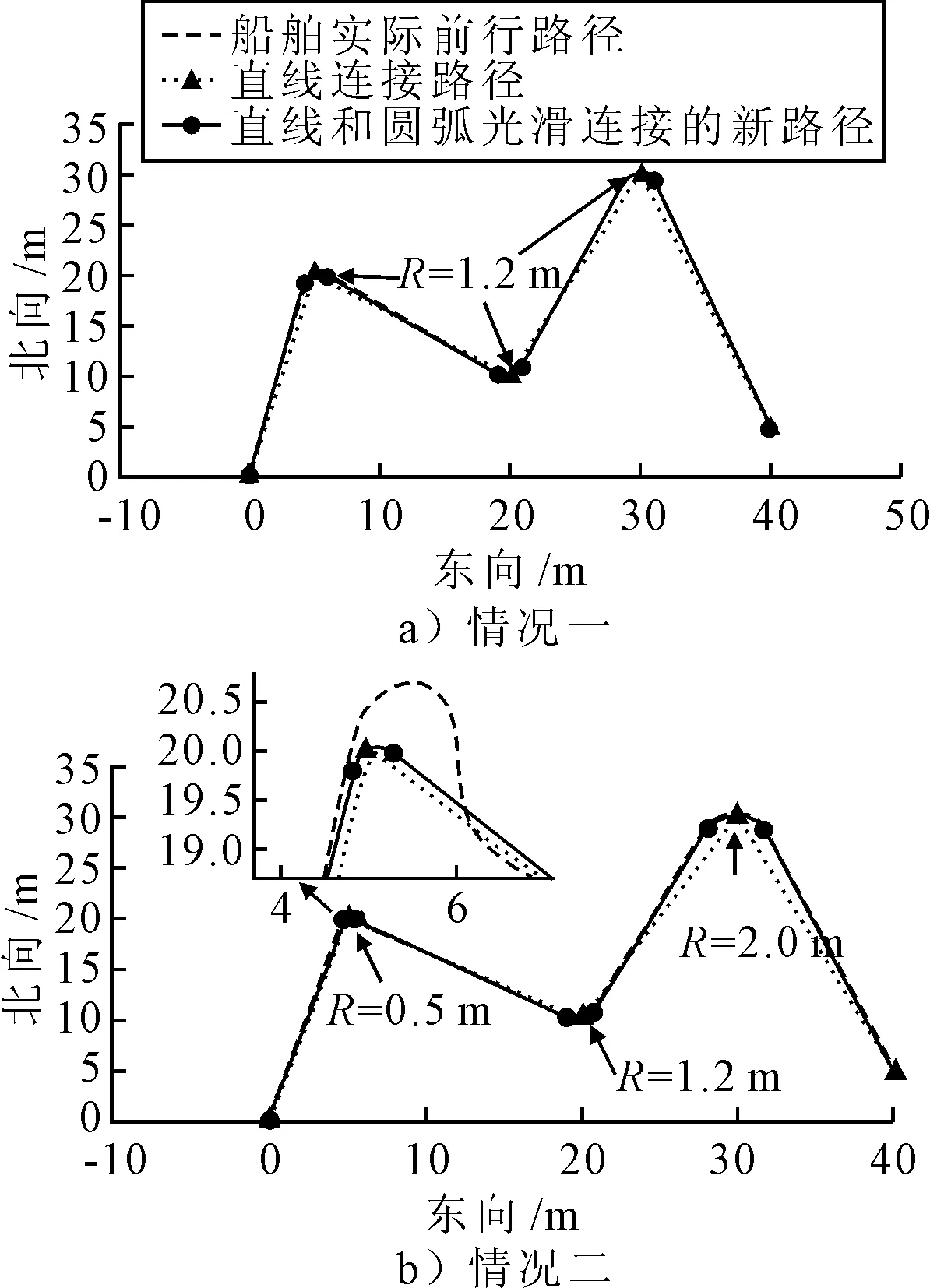
图5 无人艇运动轨迹图

图6 无人艇实际艏向角和LOS引导艏向角

图6为实际艏向角和LOS引导艏向角的变化情况，两者达到了非常好的吻合效果.但是通过比较图6a)和b)对应的圆弧半径R=1.2 m和0.5 m处艏向角的变化可知，图6b)中半径R=0.5 m时无人艇的实际艏向角和LOS引导艏向角的变化和变化率都较大，这对无人艇舵的性能提出非常高的要求.

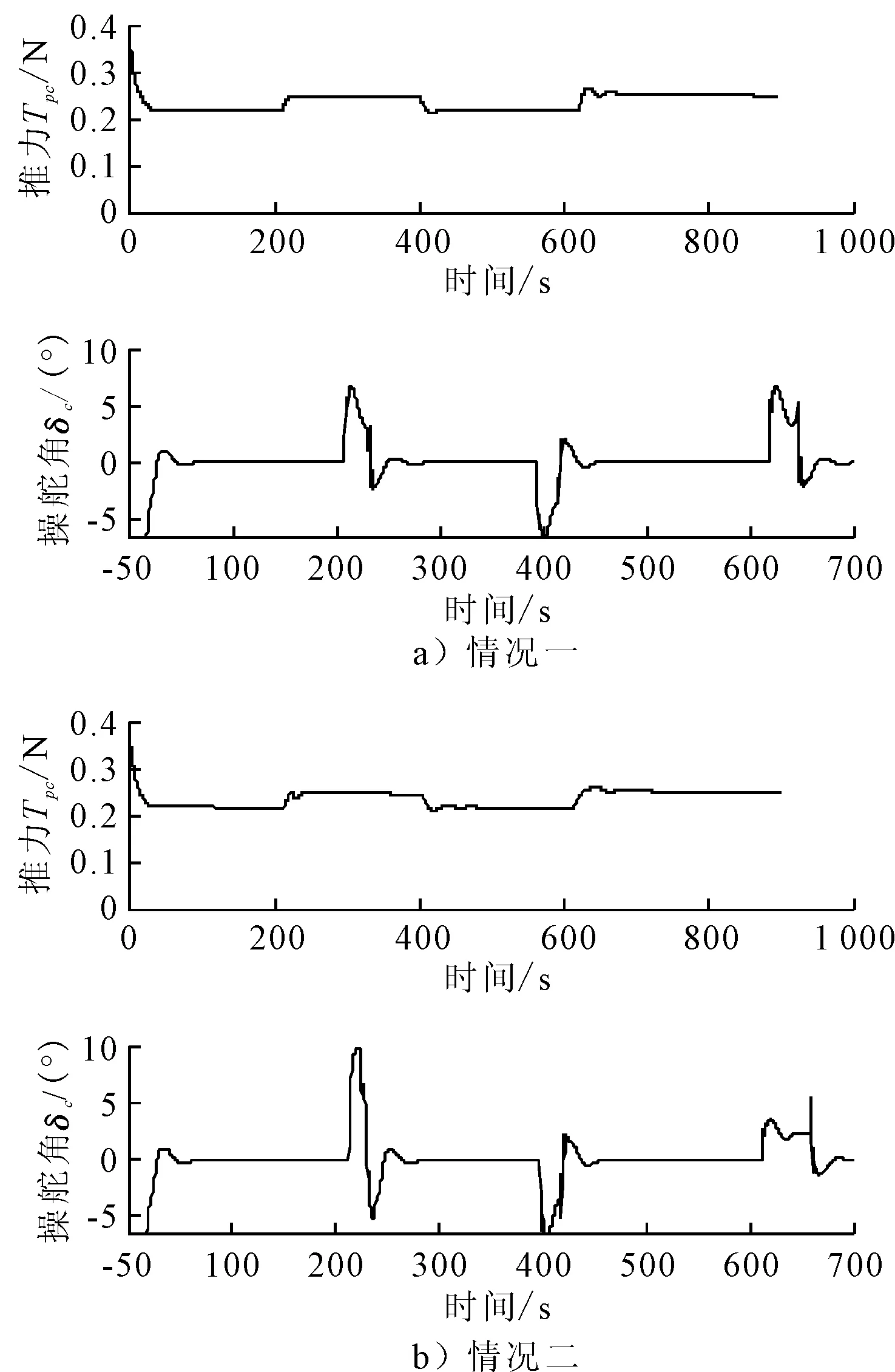
图7 螺旋桨推力和操舵角示意图

图7为螺旋桨的推力和操舵角变化情况，无人艇在两种情况下运动时螺旋桨推力大小基本一致，但在图7b)圆弧半径R=0.5 m处，无人艇产生较大的操舵角和舵角变化率.这是因为图6b)中在半径R=0.5 m处艏向角的变化及变化率较大，使无人艇要产生较大的舵角和舵角变化率才能满足其要求，如果其要求超出无人艇舵的性能所能达到的极限，将会导致图5b)中在半径R=0.5 m处实际路径与规划路径不吻合的情况.

5 结 束 语

针对主推带舵推进系统的无人艇循迹过程中过渡圆弧半径的取值问题，本文对无人艇定常回转运动时的受力情况进行了分析，提出了一种圆弧半径的近似求解方法，并采用LOS引导系统及基于反步积分和Lyapunov理论的非线性控制器实现无人艇的循迹控制.最后，设计了两组圆弧半径，并分别在两组圆弧半径下对无人艇循迹控制进行了仿真运算，仿真结果表明了所提方法在无人艇循迹过程中的有效性.