基于Cardinal样条曲线的自适应前瞻插补算法*

袁家兰，黄 艳，盖荣丽

(1.中国科学院大学，北京 100039； 2.中国科学院沈阳计算技术研究所 高档数控国家工程研究中心，沈阳 110168；3.沈阳高精数控技术有限公司，沈阳 110168；4.大连大学 信息工程学院，辽宁 大连 116622)

0 引言

数控机床在加工复杂曲面时，通常会把把曲面离散为大量微小段，当小线段的连接处加工速度方向改变时，加速度可能会产生突变，最简单的做法是将速度降为零，但是这些小线段长度较短，并且数量多，这种方法势必会造成频繁的启停，对机床造成冲击，导致加工表面不光滑，同时效率也低。因此能否实现进给速度的高速衔接，是微小线段加工的重要指标。

经过近年来的研究，文献[1]提出了速度前瞻控制的思想，文献[2-3]将直线加减速算法引入前瞻速度处理中，建立了速度衔接数学模型，并通过对拐角速度进行衔接来实现过渡，但由于使用直线加减速策略，存在加速度突变；文献[4]将基于三次多项式的加减速模型应用到转接速度的计算中，并结合速度前瞻控制实现拐角速度的平滑过渡。这些方法和模型都是在保证加工路径与编程轨迹一致的情况下，以最大加速度为约束条件计算所允许的最大加工速度，从而实现相邻程序段间转接时速度上的连续，但这种直接过渡的方法会造成加工速度低，转接点的位置难以预测的缺点。可以在保证加工轨迹在轮廓误差允许范围内，通过引入转接段牺牲实际转接点附近轨迹精度，从而实现转接时的速度连续。比如文献[5-6]提出的圆弧过渡，虽然圆弧过渡计算简单，但是存在曲率突变的问题。文献[7]提出的插入Ferguson样条，以及文献[8]提出的插入五次样条曲线和文献[9]提出的插入PH曲线计算复杂。

所以为进一步提高加工效率，同时又能够平稳过渡，本文提出在相邻线段间插入一段光滑的Cardinal样条过渡曲线，并且通过动态的自适应前瞻处理进行全局优化，该算法首先根据弦高误差、相邻线段长度和夹角以及过渡曲线弧长和最大曲率之间的关系确定Cardinal样条曲线的表达式和转接点，然后通过弓高误差和加速度曲率等要求确定加工过程中速度极小值点所允许的最大加工速度，同时为了避免相邻速度敏感点之间的速度干涉，在前瞻处理中依据S加减速进行速度调整，这样该算法对速度自适应的同时前瞻控制，可以实现提前加减速，平滑过渡。

1 三次Cardinal样条曲线的基本原理

Cardinal样条可由4个连续控制点完全确定，中间2个控制点是曲线段端点，其他两个点用于计算曲线段端点斜率。设4个连续控制点为Pk-1,Pk,Pk+1,Pk+2,设P(u)是控制点Pk和Pk+1之间的三次参数函数式，参数t为张力系数，t控制Cardinal样条与控制点之间的松紧程度，u∈[0,1],则Pk-1,Pk,Pk+1,Pk+2,4个点建立Cardinal样条的边界条件为：

(1)

控制点Pk和Pk+1处的斜率分别与弦Pk+1Pk-1和Pk+2Pk成正比。P(u)的表达式为：

(2)

则可以认为P(0)和P(1)决定了曲线段的首末端点，P′(0)和P′(1)共同决定了曲线形状，为了建立两条小线段间的过渡曲线模型，在这里选取Pm、P0、P1、Pm这三个点作为Cardinal样条的4个控制点，其中定义Pm为首末端切矢的交点，记P0和P1分别为首末端点，为保证过渡平稳，取首末端切矢的方向与线段同向，切矢交点正是相邻两微线段的交点，则：

(3)

那么曲线形状由转接点P0、P1和张力s共同决定。

为观察不同张力下的曲线，选取Pm(10,5)、P0(0,0)、P1(20,0)、Pm(10,5)为4个控制点，当s分别取1、2、3、3.5、3.85、4时，Cardinal曲线的形状和曲率变化如图1、图2所示。

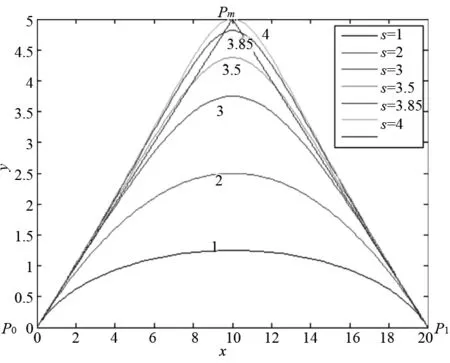
图1 曲线形状

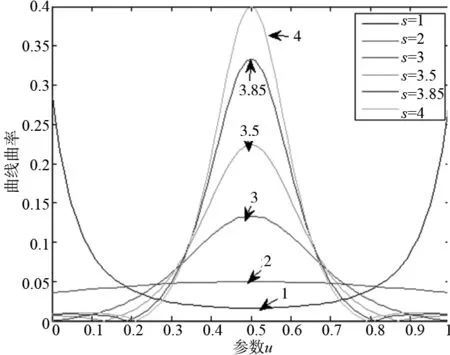
图2 曲率变化

由图可知：

(1)当s(0,3]时，弓高误差ε，随s的增大，弓高误差ε逐渐减小，当s>3,时，曲线逐渐出现超出偏差ε′,当s=3.85时，弓高误差与超出偏差相等；当s>3.85时，弓高误差进一步减小，不再是影响误差的主要因素，取而代之的是超出偏差ε′。

(2)当s[2,3.85]时，在转接点确定的情况下，随着s的增大，曲线的最大曲率逐渐增大；在误差相同的情况下，随着s的增大，曲线的最大曲率逐渐减小；当参数u=0.5时，曲率最大,当s(0,2)时，在参数u=0和u=1处曲率最大。

(3)为了减少误差和防止曲率突变，s的取值应在[2，3.85]之间。

2 三次Cardinal样条过渡算法

2.1 拐角过渡曲线矢量模型

拐角过渡曲线模型图见图3。

图3 拐角过渡曲线模型

选取Pm(htanθ,h)、P0(0,0)、P1(2htanθ,0)、Pm(htanθ,h)这4个点为控制点，为保证过渡平稳，取首末端切矢的方向与线段同向，切矢交点正是相邻两微线段的交点，则边界条件为：

(4)

则Cardinal样条曲线的矩阵表达式为：

(5)

为计算编程简便，将上面的矩阵表达式展开成直角坐标系下的多项式形式：

(6)

将点Pm(htanθ,h)、P0(0,0)、P1(2htanθ,0)带入矩阵表达式得各项系数：

(7)

(8)

那么曲线的曲率K为：

(9)

2.2 转接点位置及过渡曲线张力大小的确定

图4为过渡曲线图。

图4 过渡曲线

因为在实际加工过程中，第i段线段要同时和前后两段线段进行过渡，所以过渡距离要受到线段长度的限制，要考虑到为下一段线段留足够的过渡距离，所以最大过渡距离为：

(10)

其中，f为第i+1段线段的分割比，f=dmax/li+1此时受线段长度限制所能达到的最大高度为：

ΔH=dmaxcosθ

同时转接点的位置又受到弓高误差的约束，在满足最大弓高误差的情况下，s越大，高度h越大，所以当s=3.85时，高度h最大。

又因为高度h与弓高误差的关系：

所以最大高度h为：

此时s=3.85。

而最终高度h要同时满足这两个要求，所以h=min{Hmax,ΔH}

(1)当Hmax<ΔH时，说明只要满足弓高误差的要求，就同时满足线段长度的要求，所以取h=Hmax,弓高误差为ε,s=3.85

那么转接开始点和转接结束点的位置为：

其中，f=Hmax/ΔH。

(2)当Hmax>ΔH时,说明只要满足线段长度的要求，就能够满足弓高误差的要求，所以取h=ΔH。

此时弓高误差小于ε，速度较低，所以取最大弓高误差ε，此时张力s为：

如果求取出的s<2,则取s=2,此时允许的弓高误差可以调整为ε-0.5h。

那么转接开始点和转接结束点的位置为：

根据上述分析可知，通过控制高度h和张力，可以唯一确定Cardinal样条过渡曲线。

2.3 确定过渡曲线所允许的最大转接速度

拐角处过渡曲线的插补速度要满足机床各驱动轴的最大加速度和加加速度的要求，最大弓高误差的要求和最大加工速度的要求，在过渡曲线中，中点位置及u=0.5处的曲率最大，速度最低，只要该点的速度满足最大转接速度，其他点的速度也满足，所以必须保证该点的速度小于所允许的最大转接速度。其中最大曲率Kmax根据式子(9)计算。

Kmax=K(u=0.5)

最大弓高误差的限制：

在插补周期恒定的条件下，插补曲线时产生的弓高误差随曲率和加工速度的增大而增大，为确保插补过渡曲线时产生的弦高误差在系统给定的范围内，可根据过渡曲线的曲率来对加工速度进行限制。

最大加速度的限制：

最大加工速度的限制：

V3=Vmax

其中，Emax是所允许的最大弓高误差，Vmax是机床所允许的最大加工速度，T为插补周期，Amax为最大加速度为保证加工过渡曲线符合加工要求满足弦高误差和机床机械特性的限制，所允许的最大加工速度应取最小值。

Vi=min{V1,V2,V3}

如图5所示，加工轨迹的长度包括两段过渡弧长的一半和中间的线段，其中si-1为第i-1段的过渡弧长，si为第i段的过渡弧长，lmi为第i段的中间直线段。

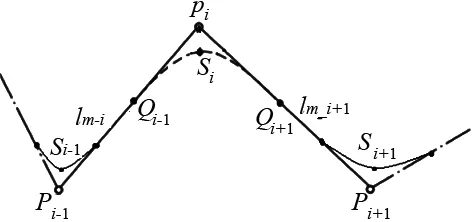
图5 运动轨迹

x′(u)2和y′(u)2根据公式(6)可得。

3 前瞻控制

转接速度受到弓高误差、加速度和曲率的限制，具体求解参考2.3节，此时求出的转接角的进给速度不一定是最优的，还受到前后两段轨迹长度的影响，如果轨迹长度很短，长度不足以达到该段的终点速度，必须重新计算转接角所能允许的最大进给速度。而重新确定转接角的最大速度往往需要进行重新迭代才能得到最优的衔接速度，这样会产生很多冗余，所以这里采用动态自适应前瞻控制策略。

3.1 前瞻控制规划

(1)确定前瞻段数

在前瞻控制算法中，前瞻段数的选取也比较重要，选取的段数较多，前瞻时间就会过长，段数过短，效率低精度低。文献[10]提出固定段数的前瞻方法，虽然一定程度上提高了加工效率，但是段数固定不能更好的适应复杂多变的轨迹。本文根据文献[11]采用依据衔接角的角度大小动态选取前瞻段数N。

(2)前瞻具体规划

第1步：数据预读，确定前瞻段数N，并读入相应的直线段，第一段的初速度和最后一段的末速度为零，计算每个衔接角的最大限制速度Vi(参考2.3节)和拐角开始距离和拐角结束距离。

第2步：从后往前判断。从前瞻缓冲区的最后一个直线段开始，对衔接角速度进行判断，判断当前衔接角速度是否受后面线段长度的影响，如果受影响重新计算衔接角速度，如果不受影响，继续下一点的判断，直到到达缓冲区的起点。

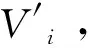
(3) 判断速度是否受线段长度影响并重新求解衔接角速度

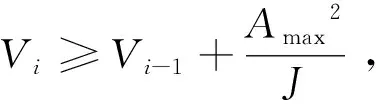
如果ΔS≤Si,在Si的长度内，Vi-1能够达到Vi,不受线段长度影响,否则受影响,重新计算受前一段线段长度影响的速度Vpre_i。

判断流程图如图6所示。

图6 速度可达性判断流程图

②同理可计算Vi减速到Vi+1受后一段线段长度影响的速度。

4 仿真测试

因为在加工过程中，加工效率主要取决于在满足精度要求的情况下，线段间转接点处所允许的最大加工速度，所以通过比较相同条件下，直接过渡法和本文算法的转接速度来比较效率。

在这里假设所允许的最大进给速度VF=30m/min,插补周期T=2ms,最大加速度Amax=3m/s2,所允许的最大插补误差Emax=1mm,相邻线段间的夹角θ(0，180)，则直接过渡法和本文算法的转接速度如图7所示。

图7 Cardinal过渡曲线和直接过渡曲线的转接速度对比图

由图可以看出，本文算法在转接点处的最大允许速度更大，说明在相同加工条件下，采用本文算法效率更高。

为进一步验证本文提出的过渡算法，对长度在0.1～1mm之间的微小线段进行加工仿真验证，并且为了使效果比较明显，这些微小线段之间的夹角大部分在140～180之间，然后从加工时间上对本文算法和直接过渡算法进行对比分析。

表1 加工时间对比表

仿真结果表明，采用直接过渡算法，加工效率低下，而采用本文算法效率提升了30%多，并且能够有效减少速度的波动，提高加工质量。所以，本文算法更加适合微小线段加工。

对于加工精度的验证，由前面2.2节的内容可知，为保证加工速度达到最大，生成的过渡曲线的最大弦高误差是所允许的最大加工误差，整个加工过程中的加工误差都不会超过所允许的最大加工误差，所以能够满足系统的精度要求。

为进一步验证，分别由本文算法和直接过渡算法对编程点(0,0,0)、(5,0,0)和(0,5,0)构成的相邻线段进行加工验证，结果如图8所示。

图8 弦高误差对比图

由结果可以看出，本文算法没有超过系统所限制的最大误差，是完全能够满足加工精度的要求的，与直接过渡算法相比，虽然误差相对会大一些，但加工时间却缩短了很多。

通过以上分析，说明了本文算法能够在保证加工精度何满足机床最大加减速能力的条件下比直接过渡法获得更高的加工效率。

5 结论

本文在深入研究现有微小线段过渡算法的基础上，提出了一种基于Cardinal样条曲线过渡模型，基于此模型提出同时满足加工精度和线段自身长度的插补算法，并详细介绍了原理。通过仿真实验表明，与直接过渡算法相比，该算法能够在保证加工精度和加工质量的条件下，有效地提高加工速度，并且采用自适应前瞻控制避免了加速度和速度突变的问题，同时该算法计算简单、误差易控，能够使微小线段间平滑过渡。