单回路500 kV输电塔风致响应参数分析*

张庆华

(华北水利水电大学土木与交通学院 郑州，450000)

引 言

高压输电塔具有轻质、高柔、小阻尼特性，风荷载已成为结构设计的主要控制因素之一。近年来，输电塔在强风作用下的破坏或功能失效屡有发生[1]，说明现行的荷载规范尚不能提供精确的格构式输电塔结构风致响应计算方法。

格构式输电塔风致动力响应计算方法可分为频域和时域方法[2-4]两类。时域法是将荷载时程直接作用在结构上，通过时程逐步积分，迭代计算结构的动力响应。时域法计算精度高，可以较方便地考虑结构的非线性效应，但时程分析数值积分计算量非常大，尤其对复杂结构考虑非线性平衡迭代时更耗费时间。频域分析方法通过振型分解将结构响应统计量描述成对应各阶振型的广义模态响应在模态空间内的线性组合，在频域内通过传递函数建立激励与响应之间的关系，描述结构的动力响应。频域法虽不能考虑结构非线性效应，但概念清晰、计算效率较高，可直接得到风振响应随风荷载特性和结构基本特性的变化规律，故在输电塔风致响应的研究中得到了广泛应用[5-8]。

模态叠加法是结构频域风振动力响应计算的常用方法，通过叠加各阶模态的贡献求系统的响应。输电塔作为典型的三维空间结构，外形和质量分布复杂，自振频率密集，笔者利用编制的基于非定常风荷载的结构风致动力响应频域分析程序，详细分析和讨论了参振模态数目、模态交叉项、结构阻尼比等参数对典型500 kV单回路酒杯型输电塔风致动力响应计算结果的影响。

1 500 kV单回路高压输电塔

根据《国家电网公司输变电工程典型设计500 kV输电线路分册》[9]，酒杯型输电塔是国内500 kV单回路高压输电线路中最常见塔型之一。文中参数分析以典型500 kV单回路酒杯型输电塔为研究对象(见图1)，该塔全高55 m，呼高48 m，为典型角钢塔，各杆件及零部件的主要材料为Q345和Q235钢。

图1 典型500 kV单回路酒杯型输电塔(单位：m)Fig.1 Typical single-circuit 500 kV transmission tower (unit: m)

由于布置导线的需要，酒杯型输电塔头在沿导线方向(图1中y轴方向)具有较大的迎风面积和外伸质量，使得塔头在该方向与垂直于导线方向(图1中x轴方向)上的结构特征差异明显。同时由于塔头位于输电塔的顶端，对风荷载更为敏感。文中将基于风洞试验的非定常风荷载[10-11]，重点对塔头关键节点风致响应进行参数分析。

2 风洞试验方法

典型酒杯型输电塔头、塔身节段高频动态天平测力风洞试验在同济大学土木工程防灾国家实验室TJ-1大气边界层风洞中进行。天平测力试验为刚性模型试验，模型选用质地较轻又有较高刚度的有机玻璃板制作，塔头、塔身模型几何缩尺比分别为1/45，1/30。考虑到塔头、塔身节段本身高度不大，每个节段高度范围内平均风速和湍流度变化均不大，节段模型的测力试验在由被动格栅紊流发生器生成的空间均匀紊流场中进行(风场湍流度由模型中部湍流特性决定)。即对每个节段模型，试验平均风速和湍流度均沿高度不变，平均风速剖面对原型结构风力的影响在根据气动力系数计算实际结构风力时考虑。

根据《建筑结构荷载规范》[12]湍流度计算公式，对于文中所研究的C类地貌下的酒杯型输电塔，塔头、塔身湍流度约为0.194，0.165，节段测力试验均选择顺风向湍流度为19%(横风向湍流度为13%)的紊流场中完成(图2)。试验时通过转动转盘模拟不同风向。为了保证数据质量，提高系统有效频率宽度，对数据进行了数字滤波；为了消除天平模型系统对风力的放大，采用传递函数方法对功率谱进行了修正。详细的试验过程和结果见文献[10,11]。测力试验获得的输电塔节段风荷载数据将作为本研究风致响应参数分析的输入荷载。

图2 输电塔节段模型Fig.2 Section models of transmission tower

由于风洞试验中，未包含塔腿结构，塔腿约占整塔高的1/6，其所受的风力不可忽略。笔者将采用计算流体动力学(computational fluid dynamics，简称CFD)[13]模拟得到的体型系数根据准定常理论来计算塔腿结构受到的风力。

3 风致响应计算方法及基本计算参数

3.1 计算方法

由于输电塔结构模型复杂，节点较多，风力施加时，根据附属面积，直接将风力施加于关键节点(关键节点的选取及编号参见图1)。利用平稳激励下线性系统随机振动的模态叠加法，位移响应功率谱密度矩阵为

Sy=ΦH*ΦTSpΦHΦT

(1)

其中：Φ为质量归一的振型矩阵；H为传递函数矩阵，|Hi(ω)|2=[(ωi2-ω2)2+(2ζωiω)2]-1；Sp为风力谱矩阵，由高频天平测力风洞试验获得。

式(1)为精确的完全二次项组合方法(complete quaddratic combination，简称CQC)计算公式，包括了所有振型交叉项，考虑了振型之间的耦合。文中参数分析均采用CQC法完成。

工程中通常在小阻尼和参振频率为稀疏分布的假定下，将式(1)中j≠k的振型交叉项忽略掉，而得到以下近似的平方和开方法(square of sum of squares method，简称SRSS)公式

(2)

由位移响应谱，可计算得到加速度响应功率谱

(3)

基底弯矩功率谱为

(4)

其中：K为刚度矩阵；zi为节点高度行向量。

3.2 结构模态分析

对酒杯型输电塔进行模态分析，计算了前100阶模态。图3为输电塔前100阶频率分布情况。由于酒杯型输电塔是由大量杆件组成的复杂三维空间桁架结构，实际结构模态分析时，除部分整体模态外，不可避免的将会得到大量的局部杆件的振动模态，从而使输电塔高阶模态密集。图4给出了酒杯型输电塔结构前3阶整体振型，前两阶分为别为两个方向的侧向弯曲振型，第3阶为结构的扭转振型。

图3 输电塔前100阶固有频率Fig.3 The first one hundred order natural frequency of transmission tower

图4 输电塔前三阶整体模态振型Fig.4 First order integral mode shape

3.3 计算参数选取

计算输电塔结构风致响应的参数：a.地貌类型：C类；b.基本风速：离地面20 m高度处平均风速35 m/s；c.结构阻尼比：0.02；d.参振模态数目：100阶；e.频率范围为0～12 Hz。风致响应计算风向及结构坐标参见图5。

图5 风向角示意图Fig.5 Wind angle

酒杯型输电塔位移、加速度、轴力、基底弯矩等响应随风向变化情况在文献[14]中进行了详细分析，文中将主要分析参振模态的数目、模态交叉项、结构阻尼比等参数对风致响应的影响。选取有代表性的0°风向工况进行分析，其中，y轴为结构的顺风向，x轴为结构的横风向。考虑到塔头有较大的外伸质量，且位于塔的顶部，对风荷载更敏感，文中将重点对塔头风致响应参数进行讨论分析。

4 风致响应参数分析

4.1 参振模态数目

对于多模态参与振动的结构，如何选取参振模态的数目是模态叠加法面临的首要的问题。这里主要分析不同风速下，参振模态数目对输电塔脉动响应的影响。共考虑3种设计风速，分别为30，35和45 m/s。计算中分别选取了1，2，3，5，10，20，40和100阶参振模态数进行频域响应计算。沿输电塔高度方向，由低到高，分别选取主材上的关键点511，508，505，501，912，1 301，1 311和920为研究目标。3种设计风速计算结果类似，即风速对模态阶数对响应的贡献基本无影响。考虑到篇幅所限，文中主要给出了35 m/s风速下的计算结果。

4.1.1 位移响应

图6(a)为输电塔关键节点不同参振模态阶数位移响应计算结果的比较。可以看到，对于位移响应，前3阶模态(分别对应x，y向侧弯和扭转整体振型)几乎包含了全部参振模态，当参振模态数目大于3阶后，塔头部节点(如：节点912，1 301，920等)100阶参振模态与3阶参振模态位移响应的计算误差不超过5%，即高阶振动模态的影响基本可以忽略不计。随着节点高度的降低，高阶振动模态的影响不断增大，塔身下部511节点100阶参振模态与3阶参振模态位移响应的计算误差已增大至15%左右。

图6(b)给出了酒杯型输电塔塔顶节点930和横担节点1 301，1 311在0°风向的位移响应谱。可以看到，各节点x向动力响应基本上都由x向侧弯振型贡献；y向响应则是由y向侧弯振型和扭转振型贡献，这主要是由酒杯型输电塔外形决定，由于导线布置的需要，造成塔的y向迎风面面积较x向大很多(见图1)，因而扭转振型对该方向有较大的影响。节点1 311位于横担中部，扭转振型对其位移响应基本无贡献。

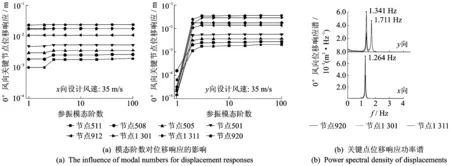
图6 位移响应Fig.6 The displacement responses of transmission tower

4.1.2 加速度响应

图7 模态阶数对输电塔加速度的影响Fig.7 The influence of modal numbers for the acceleration responses of transmission tower

加速度响应是计算等效静力风荷载的重要响应参数之一。与位移响应明显不同，由图7所示关键节点不同参振模态阶数加速度响应计算结果比较可见，参振模态数目对各关键点加速度响应值有较大的影响。随着参振模态阶数的增加，加速度响应值单调增大。

4.1.3 基底弯矩

图8 酒杯型输电塔基底弯矩Fig.8 The base bending moments of transmission tower

输电塔在风荷载作用下的基底弯矩对结构基础设计起重要的控制作用，也是等效静力风荷载计算中以基底弯矩为等效条件的弯矩阵风荷载因子法的必要条件。0°风向角不同参振模态酒杯型输电塔基底弯矩顺/横风向(y/x向)风致响应见图8(a)。其中，x向侧弯为x向基底弯矩的主要参振模态，而y向侧弯基本包含了y向基底弯矩几乎全部参振模态，高阶模态对基底弯矩的贡献很小(见图8(b))。

4.2 结构阻尼比

在进行频域计算时，文中对所有参振模态取相同的阻尼比。为了考察阻尼比对计算结果的影响，这里设置了4种阻尼比：0.005，0.01，0.02和0.03。

输电塔0°风向关键节点位移响应均方根值随阻尼比变化见图9(a)。由图可见，输电塔位移响应对阻尼比的变化比较敏感，当阻尼比由0.005增大至0.03时，位移响应减小为原来的1/3～1/2左右。

图9(b)给出了0°风向下，输电塔在不同结构阻尼比时的位移响应自功率谱。可以看到，阻尼比对响应低频部分的影响基本忽略，对共振部分影响显著，随着阻尼比的增大共振响应将明显减小。阻尼比越小，共振峰值就越陡峭，带宽也越窄；阻尼比越大，共振区响应谱曲线越平滑。

4.3 模态交叉项

模态叠加法采用的CQC计算公式(式(1))包括了所有选定振型交叉项，考虑了振型之间的耦合；而工程中通常忽略振型交叉项，采用近似的SRSS公式(式(2))计算结构的响应。针对酒杯型输电塔，通过对比CQC与SRSS方法计算结果，考察模态交叉项对频域计算结果的影响。

表1为酒杯型输电塔风致响应计算中忽略模态交叉项后的结果(SRSS方法)与考虑模态交叉项的结果(CQC方法)比较。由表可知，CQC方法与SRSS方法结果吻合较好，计算误差不会超过5%。大多数情况下，CQC方法计算结果都会略大于SRSS方法计算结果(CQC方法更偏安全)。

总的说，模态交叉项对酒杯型输电塔风致响应结果的影响很小，文中单回路酒杯型输电塔进行频域计算时，可以不要考虑模态间的交叉项。

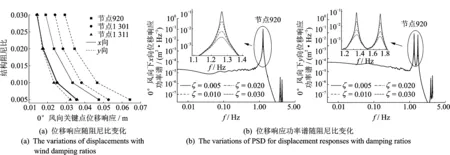
图9 阻尼比对酒杯型输电塔位移响应的影响Fig.9 The influence of damping ratios for the displacement responses of transmission tower

计算方法位移响应/m根方差值(误差)节点920节点1 301节点1 311x向y向x向y向x向y向CQC0.023 40.034 50.017 50.028 30.017 70.017 2SRSS0.023 4(0.07%)0.034 4(0.37%)0.017 5(0.02%)0.028 3(-0.01%)0.017 7(0.03%)0.017 2(0.10%)计算方法加速度响应(m2/s)根方差值(误差)节点920节点1 301节点1 311x向y向x向y向x向y向CQC1.4583.0881.0882.6931.1011.134SRSS1.449(0.64%)2.983(3.39%)1.087(0.07%)2.679(0.50%)1.101(0.07%)1.127(0.65%)计算方法基底弯矩(N·m)根方差值(误差)x向y向CQC5.355×1053.452×105SRSS5.348×105(0.11%)3.381×105(2.04%)

注：①以CQC法计算结果作为标准值；②SRSS误差=(CQC计算结果-SRSS计算结果)/CQC计算结果×100%

5 结束语

输电塔上部节点仅考虑前3阶整体振型(x，y向侧弯和扭转)即可保证足够高的位移计算精度，高阶振动模态的影响基本可以忽略不计。参振模态数目对加速度响应有较大的影响，随参振模态阶数的增加，加速度响应单调增大。基底弯矩主要有一阶侧弯振型贡献，高阶模态贡献很小。输电塔对阻尼比的变化敏感，阻尼比对响应低频部分的影响基本可以忽略，对共振部分影响显著，随着阻尼比的增大共振响应明显减小。模态交叉项对酒杯型输电塔关键点响应结果的影响较小，进行频域计算时，可不考虑模态间的交叉项的影响。