基于改进多尺度模糊熵的滚动轴承故障诊断方法*
2018-11-01郑近德代俊习朱小龙潘海洋潘紫微
郑近德, 代俊习, 朱小龙, 潘海洋, 潘紫微
(安徽工业大学机械工程学院 马鞍山,243032)
引 言
由于制造误差和装配不当等原因,滚动轴承在运转过程中必然会产生振动[1]。当轴承出现局部故障时,振动信号随之会表现出非线性、非平稳特性。直接从这些信号中提取故障特征将变得尤为困难。随着非线性科学理论的发展,很多非线性理论和方法,如小波分析、分形维数、近似熵等已被广泛应用于故障诊断领域[2-7],并取得了不错的效果。如文献[6]将经验模态分解(empincal mode decomposition,简称EMD)分解的IMF分量与灰色关联模型结合建立IMF的能量分布,从而实现故障类型的诊断;文献[7]将分形维数与近似熵用于度量信号的复杂性,结果表明近似熵具有一定抗噪和抗野点的能力。针对近似熵存在自匹配的缺陷,Richman等[8]提出了样本熵的概念,样本熵作为常用的一种特征提取方法,具有抗噪能力强、所需时间序列短等优点,但是该方法只能从单一尺度描述故障特征状态。Costa等[9-10]在样本熵的基础上提出了多尺度熵(multi-scale entropy,MSE),用来衡量时间序列在不同尺度上的复杂性。针对MSE中样本熵相似性度量易发生突变,郑近德等[11]结合模糊熵的概念,提出了多尺度模糊熵(multiscale fuzzy entropy,简称MFE),并将其应用于滚动轴承的故障诊断。
MFE是一种有效的衡量时间序列的复杂性方法,与单一尺度熵值相比,其既能在整体上反映动力学特征,又能从细节上揭示其演化特性,包含了更多的模式信息[12]。然而,研究发现,MFE中的多尺度粗粒化过程会导致熵值在较大尺度处的波动,产生端点“飞翼”现象[13]。为此,文中采用滑动均值求数据点间均值的方式改进粗粒化过程。在此基础上,提出了改进的多尺度模糊熵(improve multi-scale fuzzy entropy,简称IMFE)。改进后的多尺度过程综合考虑了相邻数据点的信息,不仅克服了时间数列变短的缺陷,而且能够提取更多的故障特征信息。
最后,笔者将改进多尺度模糊熵与支持向量机结合,提出了一种新的滚动轴承故障诊断方法,并将其应用于试验数据分析。结果表明,所提方法能有效地利用少量的训练样本得到较高的故障识别率,是一种有效的故障诊断方法。
1 多尺度模糊熵算法
1.1 多尺度模糊熵算法
多尺度模糊熵的计算步骤[11]如下
1) 设原始数据为{Xi}={X1,X2,…,XN},建立粗粒化过程
(1)
其中:N为数据长度,τ=1,2,…,为尺度因子。
τ=1时,yj(1)为原数据{Xi};τ>1时,原数据被分割成τ段长度不超过N/τ的粗粒序列{yj(τ)}。
2) 对得到的τ个粗粒序列分别求其模糊熵,并把熵值画成尺度因子的函数。模糊熵的定义参考文献[14-15]。
由式(1)粗粒化过程可以发现,尺度因子越大,粗粒化序列长度越短,熵值的偏差会随着粗粒化序列长度减小而逐渐增大。不仅如此,以尺度因子τ等于2为例,粗粒化方式如图1所示。当尺度因子等于2时,粗粒化考虑了X1和X2,X3和X4等之间的信息,而没有考虑X2和X3、X4和X5等之间的信息,造成了信息的遗漏。为此,文中借鉴滑动均值的思想,提出了改进多尺度模糊熵算法。

图1 尺度因子等于2时的多尺度化方法Fig.1 Multiscale methods for scale factor equal to 2
1.2 改进的多尺度模糊熵
IMFE的计算步骤如下
1) 设原始数据为{Xi},建立改进粗粒化过程:
(2)
当τ>1时,原始数据{Xi}被分割成τ段长度为N-τ+1的序列{yj(τ)}。
2) 对得到的τ个改进粗粒序列分别求其模糊熵,并将其画成尺度因子的函数。
为了说明IMFE与MFE的区别,以尺度因子2为例,改进的多尺度算法如图2所示。
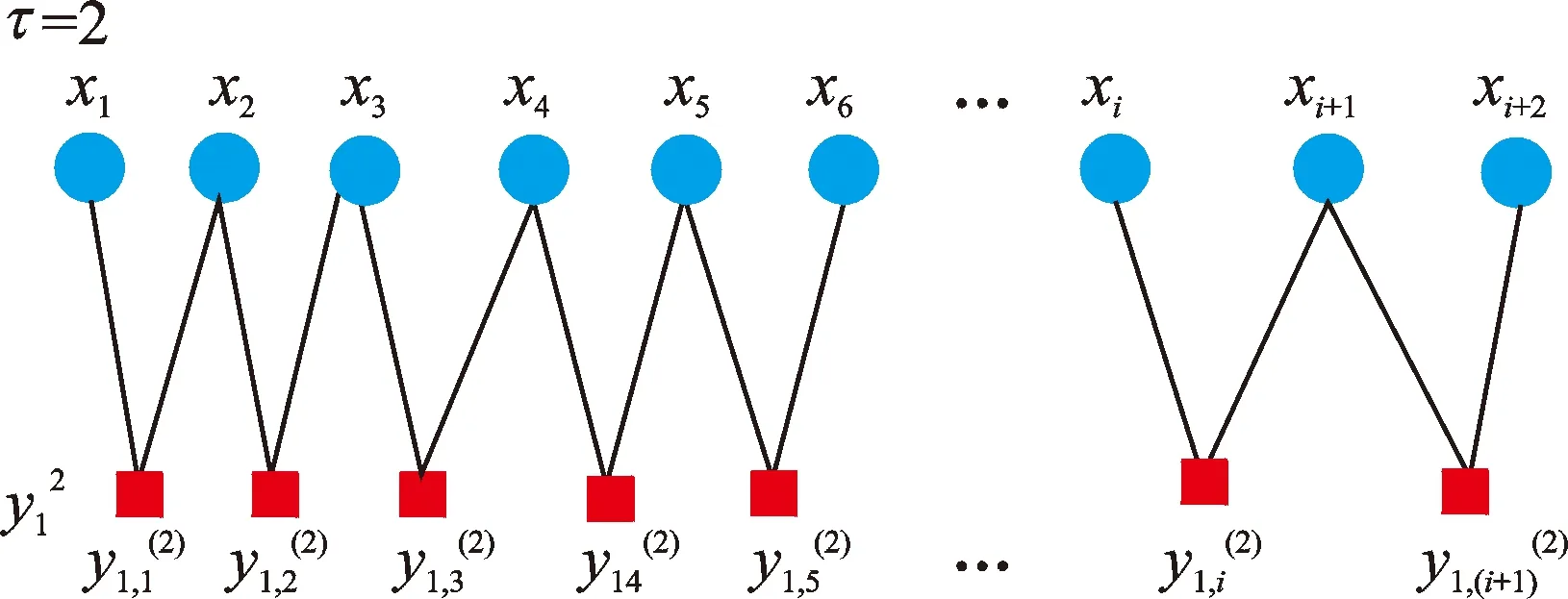
图2 尺度因子等于2的改进多尺度方法Fig.2 The improved multi-scale method with scale factor equal to 2
由图2可知,尺度因子等于2时,改进的多尺度化法综合考虑了2个相邻数据点特征信息,避免了由于粗粒化不足而导致信息的遗漏。
2 IMFE与MFE对比分析
2.1 参数选择
IMFE的计算与数据长度N,嵌入维数m、相似容限r以及指数函数梯度参数n有关。首先,m取值越大就会有越多的详细信息,但所需数据就更长(N=10m~30m),综合考虑,m=2。其次,相似容限r表示模糊函数边界的宽度。r选择过小会统计过多的信息,导致对噪声敏感;选择过大会丢失过多统计信息,一般取0.1~0.25RSD(RSD为原始数据的标准差),文中取r=0.15RSD。再次,当n趋于无穷大时,指数函数即变为单位阶跃函数。为了尽可能的捕获有用的细节信息,文献[15]建议计算时取较小的整数值,文中取n=2。最后,数据长度对熵值的影响都比较小,文献[16]表明模糊熵比样本熵计算所需的数据长度更短,综上考虑,取N=2 048。
2.2 IMFE与MFE对比分析
首先,以相同长度的高斯白噪声和1/f噪声为研究对象。对不同的r=0.05RSD,0.1RSD,0.15RSD,0.2RSD和0.25RSD分别计算二者的MFE和IMFE,结果如图3所示,其中m=2,最大尺度因子取20。由图3可知,首先,相似容限对MFE和IMFE的计算结果影响较大,r越大,熵值越小,r越小,熵值越大,选择过大会丢失掉很多统计信息,过小估计出的统计特性的效果不理想。另外,IMFE比MFE熵值曲线光滑,且不同r的IMFE曲线差异较小,说明IMFE对r的依赖更小。综合考虑,取r=0.15RSD。

图3 相似容限对熵值的影响Fig.3 The influence of r on entropy values
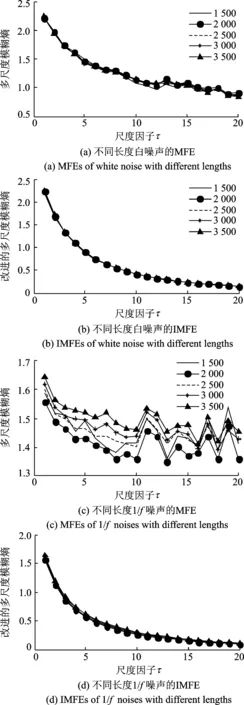
图4 时间序列长度对熵值的影响Fig.4 The influence of data length on entropy values
为了说明时间序列长度对IMFE的影响,分别取数据长度为1 500,2 000,2 500,3 000和3 500点的高斯白噪声和1/f噪声作为研究对象。分别计算二者的MFE和IMFE,结果如图4所示,其中m=2,r=0.15RSD,最大尺度因子取20。从图4中可知,IMFE的变化趋势随尺度因子的增大而逐渐光滑递减,而MFE曲线随着尺度因子的增大有波动现象,这说明IMFE稳定性更好。另外,由图4(c~d)可知,1/f噪声的MFE曲线随着尺度因子的增大稳定在一个恒定值附近,但时间序列的长度对熵值的影响较大,而不同长度1/f噪声的IMFE曲线几乎重合,且都是随着尺度因子的增大而逐渐递减,曲线比较光滑,说明其对时间序列长度的依赖性更小、更稳定。因此,上述分析结果表明,IMFE和MFE都能够有效地反映时间序列的复杂性信息,但与MFE相比,IMFE熵值更稳定、曲线更光滑,对时间序列的长度和相似容限的依赖性更小。
3 应用分析
3.1 同种故障程度试验数据分析
为了说明IMFE的有效性,采用美国Case Western Reserve University的试验采集的滚动轴承数据对其进行验证[17]。测试轴承为6205-2RSJEMSKF深沟球轴承,直径为0.533 4 mm,故障深度为0.279 4 mm,转速为1 797 r/min,采样频率为12 kHz,选用内圈(inner race,简称IR)、外圈(outer race,简称OR)、滚动体故障(ball element,简称BE)和正常(norm)四种状态的振动信号,振动信号时域波形如图5所示。
现将提出的方法应用于上述试验数据,具体步骤如下。
1) 正常、内圈故障、外圈故障和滚动体故障试验数据,每种状态取58个样本,共得到232个样本,计算所有样本的IMFE,得到故障特征集T,尺度因子τmax=20;将每一类的特征集的58个样本随机分为5个训练样本特征集T1和53个测试样本集T2。

图5 滚动轴承振动信号的时域波形Fig.5 Time domain waveforms of vibration signal of rolling bearings
2) 将训练样本特征集,输入到基于SVM建立的多故障分类器进行训练。其中,基于SVM的多故障分类器采用偏二叉树思想建立,如图6所示。SVM1中1表示正常,-1表示外圈故障、内圈故障和滚动体故障;SVM2中1表示滚动体故障,-1表示内圈故障和外圈故障;SVM3中+1表示内圈故障,-1表示外圈故障;SVM4中表示是外圈故障,-1表示其他故障。F表示支持向量机最优分类函数。SVM采用LibSVM程序[18]。SVM的核函数选取高斯径向基函数,采用粒子群算法[19]对支持向量机惩罚参数c和核函数参数g进行优化。
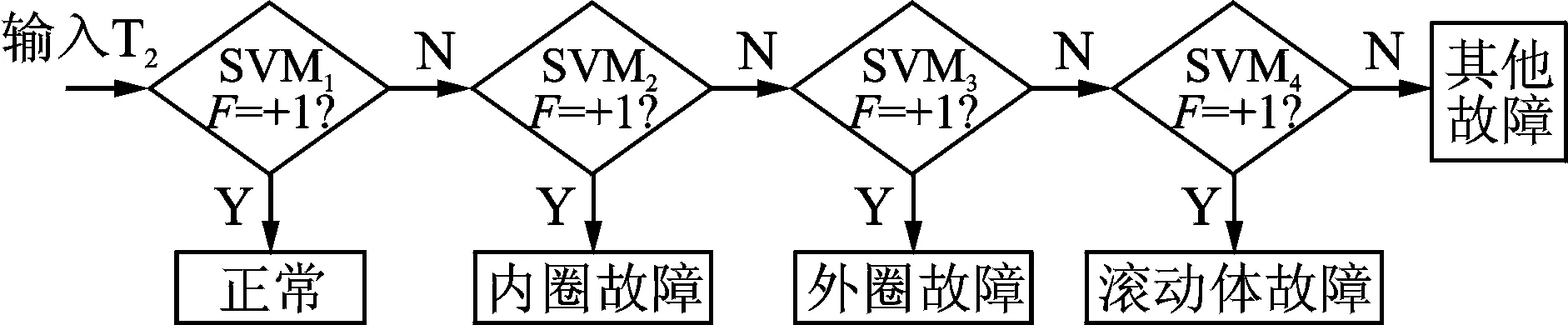
图6 多故障支持向量机分类示意图Fig.6 Sketch of multi-fault support vector machine classification
3) 在分类测试中,将测试样本集T2依次输入到已训练的SVM1,若判别式F输出为+1,则确认为正常,测试结束;否则自动输入SVM2,直到SVM4。若输出为+1,则说明测试样本属于滚动体故障。随机选取每类振动信号的5组数据作为训练样本,将剩下的53组数据作为测试样本,由于测试样本较多,文中只列出了该方法测试样本诊断结果,如表1所示。从表1可以看出,笔者提出的滚动轴承故障诊断方法对试验数据的识别率达到100%。

表1 文中方法测试样本的诊断结果
不失一般性,在相同条件下,采用MFE提取上述滚动轴承的振动信号的故障特征,并采用上述故障分类器进行识别。对于相同个数的训练样本和测试样本,输出结果中,滚动体故障中的6个测试样本被错分到内圈故障中,故障识别率为97.17%,低于笔者所提方法。
同时,为了研究训练样本个数对故障识别率的影响,分别选用5,10,15,20和25个训练样本进行训练,MFE与IMFE的故障识别率如表2所示。由表2可以看出,无论是用较少还是较多训练样本,基于IMFE的故障诊断方法都略高于基于MFE故障诊断方法。这说明:与MFE相比,基于IMFE与SVM相结合故障诊断方法更适合小样本的滚动轴承故障诊断。
表2不同数目训练样本对识别率的影响
Tab.2Theinfluenceofdifferenttrainingsamplesonrecognitionrate

%
3.2 不同故障程度的试验数据分析
为了验证所提方法的适用性,再将其应用于不同故障程度的滚动轴承试验数据。为方便,“滚动体1”、“内圈1”、“外圈1”故障滚动轴承的故障直径为0.177 8 mm,深度为0.279 4 mm;“滚动体2”、“内圈2”、“外圈2”故障滚动轴承的直径为0.533 4 mm,故障深度为0.279 4 mm。电机转速为1 730 r/min,采样频率为12 kHz,数据点数为2 048,共得到406组数据。
采用文中方法对上述数据进行分析,测试样本的输出结果表3所示。由表可以看出,论文方法将“外圈2”的两个样本错分到“内圈1”故障类中,故障识别率为99.06%。而当采用MFE进行特征提取时,“外圈2”的4个测试样本被错分到“外圈1”中,故障识别率为98.11%,低于文中方法的识别率。
当训练样本个数分别为5, 10, 15, 20和25时,对于不同故障程度的滚动轴承试验数据,基于MFE与IMFE的故障诊断方法的识别率如表4所示。由表4可知,当训练样本选用20或者以上时,两种方法的故障识别率均为100%。而当训练样本个数较少时,基于IMFE的故障诊断方法的识别率要高。一般地,对于大型机器来说,故障信号采集比较困难,故障样本个数极其稀有,而笔者提出的方法为解决小样本故障识别问题提供了一种有效的途径。

表3 测试样本的输出结果

表4 MFE与IMFE识别率
4 结束语
笔者提出了一种衡量时间序列复杂性的改进多尺度模糊熵算法,将其与多尺度模糊熵进行了对比,结果表明了所提方法的优越性。提出了一种基于改进多尺度模糊熵和支持向量机的滚动轴承故障诊断方法,通过分析具有相同和不同故障程度的滚动轴承的试验数据,将其与多尺度模糊熵进行了对比,结果表明,当样本个数较少时,论文方法的识别率更高。综上所述,改进的多尺度模糊熵有效地弥补了多尺度模糊熵中粗粒化过程的缺陷,在滚动轴承振动信号的故障特征表征方面具有一定的优势。笔者将进一步对其理论进行研究和完善,以期能推广到其他故障诊断领域中。
