干井筒下套管作业时的最大允许遇阻载荷分析
2018-11-01狄勤丰滕学清王文昌娄尔标
李 宁, 狄勤丰, 滕学清, 王文昌, 张 权, 张 涛, 杨 沛, 娄尔标
(1中国石油塔里木油田分公司 2上海大学上海市应用数学和力学研究所)
气体钻井相比钻井液钻井,其具有机械钻速高、对地层伤害小、井下漏失事故少等优点,然而在其固井作业中常因介质转换而发生井漏、井壁坍塌、卡钻等复杂情况,影响整体时效[1-10]。为此,直接在空气介质中进行下套管作业的干法固井技术应用日益广泛。
由于气体钻井形成的井眼并不光滑,特别是在砾石层段,井壁容易出现不规则的凸起或台阶,并可能造成套管下入遇阻。此时,作业人员的通常做法是通过释放悬重的方法来增加套管下端对遇阻物的作用力。这种情况下,套管遇阻载荷突然释放,整个套管柱将发生振动,并在套管中产生附加冲击载荷,使得大钩载荷(包括动载)可能超过钻机额定悬重,造成事故。
在以往的研究中,人们更多地关注钻柱的振动响应问题[11-18],但对于套管柱这种具有超长细比特征的复杂结构轴向振动问题的研究很少,而在气体钻井干法固井方式下的下套管遇阻问题的研究尚未见报道。本文利用多自由度及连续振动理论研究考虑结构阻尼的套管柱下放遇阻、突破后产生的动态载荷。
一、套管柱下放遇阻的突然释放模型
干法固井方式下,套管管柱的遇阻突然释放问题可简化为如图1所示模型。为了简化分析难度,图1中没有考虑井眼弯曲、套管扶正器及套管变截面存在的情况。

图1 套管遇阻示意图
实际情况下,干法固井时,套管具有自身的结构阻尼,其可用Rayleigh阻尼模型表示[19-20]:
C=αM+βK
(1)
式中:C—系统的阻尼矩阵;M、K—分别为结构的质量矩阵和刚度矩阵。
对于结构阻尼来说,管柱振型及受力与阻尼系数α、β关系十分密切,其可由式(2)及式(3)确定。

(2)

(3)
式中:ωi、ωj—无阻尼系统自由振动的第i、j阶特征值,i,j=1…n;ξi和ξj—相应于第i和第j阶振型的阻尼比,由实验确定。一般可取i=1,j=2。
管柱的振动方程为[19]:

(4)
广义坐标下的稳态响应为:
(5)
式中:[u]—无阻尼自由振动的位移函数。
(6)
其中:
(7)
(8)
R(t)=uTF(t)
(9)
套管下入遇阻释放后,其仅受重力和顶端悬重的作用,因此外载荷为一常量,即Ri(t)与时间无关,则最大惯性力为时间t的函数:

(10)
对于具有超长细比特征的套管柱,若不考虑阻尼影响,可以利用连续体的振动方程得到套管柱遇阻释放的动力学精确解[21]:
(11)

(12)
式中:E—套管弹性模量,Pa;ρ—套管密度,kg/m3;u—管柱轴向变形量,m;q—单位长度重力,N/m。
对于套管遇阻时,其初始条件为:
ut=0=f(x)
(13)
(14)
式中:f(x)—下端遇阻载荷造成的套管的轴向变形量。
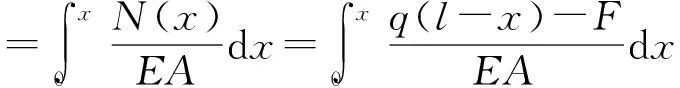
(15)
式中:N(x)—轴向力(拉为正,反之为负),N;F—杆端遇阻力(方向向上、指向截面),N;A—套管横截面面积,m2。
根据边界条件,确定系数,得到套管振动的位移函数为:

(16)
任意时刻、任一截面的加速度为:

(17)
则惯性力为:

(18)
阻力释放瞬时t=0,代入式(18),并且:
(19)
最终得到套管遇阻力突然释放瞬时产生的最大惯性力为:
(20)
管柱遇阻释放前静反力为-F。因此可以说,当不考虑阻尼影响时,遇阻释放瞬时管柱产生的纯动反力(最大动反力)等于释放前一刻套管底端遇阻载荷的一倍。
二、实例分析
在现场实际中,套管密度为7 863 kg/m3,计算中所采用的套管总长度为3 850 m,外径为0.374 7 m,内径为0.337 4 m,当遇阻力为600 kN时,计算得到其底端动载的变化规律见图2。
从图2中可看出,当考虑结构阻尼影响时,附加动载随时间衰减(衰减速率由结构阻尼系数而定),但其最大值范围为-600~600 kN。
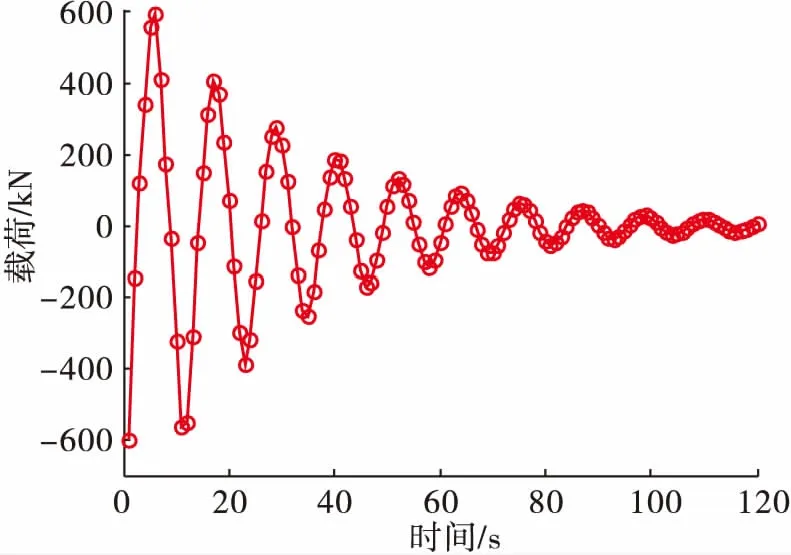
图2 考虑阻尼时套管的附加动载变化
根据精确解式(16)~式(18),可得套管在自重作用下随时间变化的振动模态如图3所示。

图3 考虑自重作用时套管在不同时刻的变形量
从图3中可以看出,套管在底端遇阻时具有初始变形,呈现上部拉伸,下部受压缩的状态,当遇阻力突然释放,套管的轴向变形将随时间产生波动。
管柱不同时刻加速度曲线如图4所示。从图中可以看出,当底端出现瞬态激励时,加速度峰值随时间沿着超细长套管柱轴线纵向传播,由于受管柱自重影响,加速度峰值与深度呈反比,其最大值为14.1 m/s2,出现在管柱端部。

图4 套管在不同时刻的加速度曲线
根据式(12)可得,套管中的波速为5.189 km/s,因此,对于3 850 m长的套管柱,因遇阻载荷突然释放造成的冲击波传播到顶端仅需要0.74 s。套管顶端附加动载的变化规律,如图5所示。从图5中可看出,顶端载荷受动载影响发生波动,产生了最大幅度为600 kN的变化,但此影响随时间衰减,顶端载荷最终趋于稳定。

图5 套管顶端附加动载变化
根据以上结果进行分析,若矿场采用8 000 m钻机进行下套管作业时,其额定悬重为6 750 kN。当井液密度为1 800 kg/m3时,钻机悬重余量约为1 380 kN(考虑附加动载影响)。对于干法固井,本例中3 850 m套管重量已达到6 188 kN,当遇阻载荷突然释放时,根据附加动载的计算,套管瞬时悬重将达6 788 kN,超出钻机额定范围,极易发生危险。因此,进行干法固井时,必须对气体钻井套管遇阻载荷突然释放附加动载进行分析,并确定遇阻载荷的极限值,这对保证钻井安全十分重要。
三、结论
(1)套管下入遇到井壁凸起或台阶的阻碍,将形成遇阻载荷。一旦这种遇阻载荷突然释放,就会在顶端大钩产生约为1倍于遇阻载荷的附加动载。气体钻井干法固井时,由于浮力作用消失,大钩载荷较大,此时这种附加动载将会给实际作业带来很大风险,必须加以重视。
(2)遇阻载荷突然释放产生的最大动载与释放前的遇阻力相同,但呈现衰减的趋势,其衰减速率受阻尼形式决定。
(3)不考虑阻尼影响的套管柱连续系统振动模型的精确解可视为干法固井套管下入时的极端情况,可以作为数值解的验证,也即气体钻井干法固井下套管作业时的最大允许遇阻载荷。
