天然裂缝性地层漏失压力预测新模型
2018-11-01王晓鹏袁伟伟
张 磊, 王晓鹏, 谢 涛, 林 海, 袁伟伟
(中海石油(中国)有限公司天津分公司)
在天然裂缝发育的地层钻井时,裂缝性漏失是一种常见的井下复杂情况[1-3],而准确预测漏失压力是提高地层防漏、堵漏成功率的前提。国内外对漏失压力的研究普遍基于完整性地层,假设漏失压力近似等于破裂压力[4-5],然而裂缝性地层的漏失机理不同于完整性地层,其漏失压力远小于裂缝性地层的破裂压力,并不适用上述假设。另一方面,目前存在的裂缝性地层漏失压力模型是基于经验公式或基于统计学[6-10],经验模型在实际应用时难以准确确定经验系数,而统计模型前期统计工作量大,不适用于认识较少的区块。为此,笔者针对裂缝性地层天然裂缝的特点,根据裂缝性漏失机理,建立了基于裂缝与井筒相交处应力状态的新模型,据此求解裂缝性地层的漏失压力,为现场钻井液密度的选择提供依据。
一、裂缝性漏失机理
发生裂缝性漏失,需要具备以下三个必要条件[11-12]:①钻井液柱压力大于地层压力;②地层中存在钻井液的漏失通道,并存在可容纳一定量钻井液的存储空间;③钻井液中固态颗粒未能在漏失通道处形成稳定架桥。
裂缝性漏失分为天然裂缝性漏失和诱导裂缝性漏失。天然裂缝性漏失指原始地层中存在开度很小的非致漏天然裂缝,在钻井液柱压力的作用下,非致漏裂缝逐渐扩展,直到扩展到致漏裂缝并与地层中其它裂缝连通时,钻井液就由正常滤失转化为裂缝性漏失,如图1所示。诱导性裂缝漏失指地层不存在天然裂缝,在钻井液压力的作用上形成诱导裂缝,进一步扩展且与其它诱导裂缝连通,从而发生裂缝性漏失。通常诱导缝方位与水平最大主应力方向一致,并伴有两组高角度的共轭剪切缝。

图1 裂缝扩展模拟示意图
二、天然裂缝性地层漏失压力模型
1. 模型思想与基本假设
当井筒周围发育裂缝时,在钻井液的作用下裂缝扩展发生漏失。由于井周地层所受应力距井筒距离的增加而呈下降趋势,裂缝扩展首先从与井筒相交处开始。因此建立了井筒与裂缝相交的力学模型,研究相交处的应力状态,认为相交处发生扩展的液柱压力即为裂缝性地层的漏失压力。
模型假设如下:①基于岩石力学井壁围岩应力分布模型假设基础;②井筒周围存在许多开度很小的天然裂缝;③裂缝在地层中形状不规则且有开度,并基于文中[13]推导裂缝宽度模型时认为与井眼斜交的裂缝在井壁上呈一标准的圆,本文为了尽量符合实际情况的前提下简化计算,认为裂缝与井眼相交处为非常小的圆环面;④裂缝内部被地层流体充满,压力近似为孔隙压力。
2. 模型的建立
2.1 井壁围岩应力分布
考虑岩石为小变形弹性体、井壁围岩处于平面应变状态、符合线性叠加原理,得到了斜井井壁围岩的6个应力分量[14]:
σr=pw
σθ=-pw+σxx(1-2cosθ)+σyy(1+2cosθ)-
4σxysin2θ
σz=σzz-u[2(σxx-σyy)cos2θ+4σxysin2θ]
σrθ=0
σrz=0
σθz=-2σxzsinθ+2σyzcosθ
(1)
式中:σr、σθ、σz、σrθ、σrz、σθz—柱坐标中的应力分量,MPa;pw—井内液柱压力,MPa;σxx、σyy、σxy、σzz、σxz、σyz—地应力分量,MPa;θ—地层中某点径向与水平最大主应力方向的夹角,°;u—泊松比,无因次。
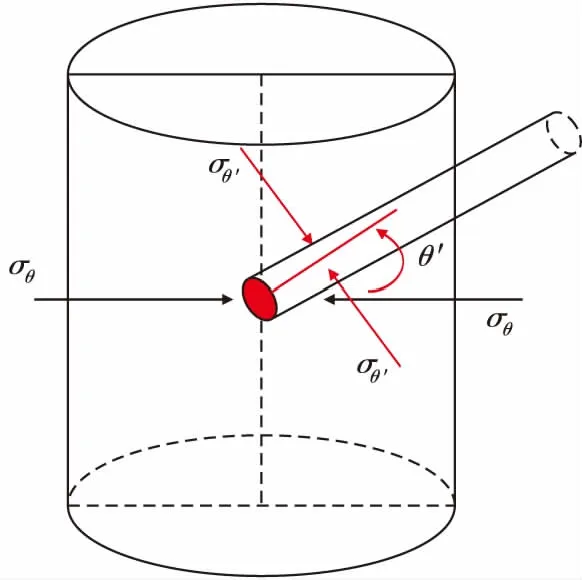
图2 裂缝与井筒相交模型示意图
2.2 裂缝与井筒相交圆环面应力分布
建立如图2所示的力学模型,其中裂缝与井筒相交,θ′表示相交圆环面处任一点与中心的连线和井壁围岩σθ方向的夹角。基于弹性力学平面应变模型,以井壁围岩应力为远场地应力,研究裂缝与井筒相交处的应力状态时,先研究各应力分量对裂缝与井筒圆环面应力的影响,再进行叠加。具体推导过程如下。
2.2.1 作用于裂缝壁面的液柱压力pm引起的应力
对于裂缝与井眼相交处圆环面来讲,作用在裂缝壁面上的液柱压力pw为径向力之一,而裂缝本身也被流体等填充成充满的状态,认为裂缝内流体产生的压力与孔隙压力相同,因此作用于裂缝壁面处的液柱压力pm为:
pm=pw-pi
(2)
而pm在圆环面处引起的应力为:
(3)
2.2.2 井壁围岩应力σz引起的应力


=σz-2σzcos2θ′

(4)
2.2.3 井壁围岩应力σθ引起的应力


=σθ+2σθcos2θ′
(5)
2.2.4 井壁围岩应力σr引起的应力

=σr-2ν(σz-σθ)cos(2θ′)
(6)
2.2.5 井壁围岩应力σθz引起的应力



(7)
2.2.6 井壁围岩应力σrz引起的应力


(8)
2.2.7 井壁围岩应力σrθ引起的应力


(9)
经过线性叠加,得到由井壁围岩应力引起的裂缝与井眼相交圆环面处的6个应力分量:
(10)
3.模型求解
借鉴破裂准则,裂缝性地层裂缝扩展时无需抵抗岩石抗拉强度,因此井壁上任一点处的最小主应力为0时得到的压力即为漏失压力。
采用数值方法求解漏失压力时,根据裂缝圆环面应力分布模型,对于某一深度分别计算各个周向角下裂缝圆环面的应力状态,选取各个周向角下漏失压力的最小值作为该深度处的漏失压力,从而求得全井深的漏失压力剖面,流程图如图3所示。

图3 新模型求解流程图
三、实例计算
渤中34-9区块沙河街组是典型的微裂缝发育地层,其中71%的漏失属于裂缝性漏失。根据本文裂缝性漏失压力模型,计算出5口井漏失点处的漏失压力,并实际井底压力进行对比,如计算得到的漏失压力小于实际井底压力,则表明本模型计算结果符合现场实际情况。结果如表1所示,计算结果满足实际工况,表明本模型能够准确地预测裂缝性地层的漏失压力,能够为现场钻井液密度的选择提供依据。

表1 渤中34-9区块5口探井漏失压力与井底压力对比
注:“符合”表示计算求得漏失压力符合现场实际情况。
四、结论
(1)裂缝性漏失分为天然裂缝性漏失和诱导裂缝性漏失,非致漏裂缝在钻井液的作用下逐渐扩展并与其它裂缝连通,从而导致裂缝性漏失。
(2)基于井壁围岩应力状态的基础,建立了裂缝与井筒相交的力学模型,研究相交处圆环面的应力状态,认为最小主应力为0时的液柱压力即为裂缝性地层的漏失压力。
(3)实例分析表明,创新建立的漏失压力模型针对性强,具有科学依据,预测结果与实际情况吻合,可为现场钻井液密度的优化设计提供依据。
(4)漏失压力是地层漏失性质中的一个重要组成部分,目前研究仍处于起步阶段,建议进一步加强研究,以指导安全钻井。
