气柜加肋壳体结构的抗震弹塑性性能分析

(安徽工业大学建筑工程学院，安徽马鞍山243032)

随着大型化生产的需求，30万m³圆筒形气柜已成为钢铁企业常用的储气设备，它的主体结构是高约100 m、直径约为60 m的加肋筒体。其结构形式上的改进和受力性能一直被设计研究领域所关注[1]。已有研究尝试对活塞与筒体之间密封材料的减震效能进行分析[2]；对气柜加速度响应的现场实测表明，活塞位于3/8柜体高度工况下的结构动力特性参数得到识别[3]；运用精细化模型对其分析，结果表明背景能量参与系数法用于对影响气柜脉动风振响应的主模态进行准确识别[4]；活塞对气柜自振周期的影响分析表明，自振周期随活塞上升而增大[5]；地震作用下不同高度煤气柜的动力响应分析表明筒体高宽比控制在2∶1以内较为合理[6]；对气柜在三向地震激励下进行的弹性时程分析表明在对顶盖调平装置进行设置时应考虑最大竖向位移值的影响[7]。但是气柜结构在罕遇地震(大震)作用下的抗震性能分析仍是需要重点研究内容之一。

气柜加肋壳体的质量沿高度变化较小，环形走道是质量集中的部位，且气柜顶盖质量较大，约占气柜总质量的1/10，因此该结构在罕遇地震作用下可能出现薄弱部位从而导致重大破坏，造成有毒气体泄漏,其危害巨大。为了确保气柜在罕遇地震作用下不发生重大破坏，出现重大安全隐患，本文参考圆筒形气柜的有关垂直度的规定[8]，按照规范规定的性能2的要求[9]，以气柜筒体顶点位移角限值为1/500作为性能控制目标对气柜结构的抗震弹塑性性能进行分析。通过对气柜加肋壳体的静力和动力弹塑性分析，确定最不利的加载方式，依据初始应力条件下动力响应数据，拟合罕遇地震下该结构的顶点位移计算公式，为工程抗震的初步设计提供参考。

1 气柜加肋壳体的模型信息

某30万m3大型气柜的加肋筒体：高110 000 mm，直径为62 000 mm，筒壁带肋壁板厚7 mm，纵肋为32根H300型钢立柱，6道走道的槽型截面宽均为900 mm。气柜的顶盖为矢高6 810 mm的加肋浅球壳。气柜结构的各构件质量见表1。

表1 构件质量Tab.1 Component weight

有限元模型中，筒体壁板和顶板采用Shell181壳单元，筒体和顶盖的加劲肋采用Beam188梁单元。各构件的连接采用绑定约束，筒体底部采用固定约束。材料均为Q235B，采用理想弹塑性、双线性等向强化模型。图1为气柜和有限元模型图。该气柜的抗震设防烈度为8度，场地类别为Ⅱ类，设计地震分组为第2组，地面粗糙度为B类。鉴于一阶振型在气柜结构的抗震分析中占主导地位，根据模态分析结果，提取一阶振型的模态数据为{0,0.149,0.312,0.499,0.692,0.878,1}，进行计算得等效结构的模态质量为1599.148 kg，振型参与系数为1.364。

图1 气柜实例和有限元模型Fig.1 Gasholder instance and finite element model

2 气柜加肋壳体结构弹塑性分析

2.1 加肋壳体结构静力弹塑性分析

采用静力弹塑性能力谱法对气柜加肋壳体结构进行静力弹塑性分析，将性能点对应的谱位移转化为相应的水平地震作用下气柜结构的顶点位移，将所得顶点位移与允许位移值进行比较，判断结构在罕遇地震下的抗震性能[11]。

静力弹塑性分析的加载模式采取均布加载、倒三角形加载和基本振型加载。运用ANSYS软件分析3种加载模式下气柜结构在多遇地震(小震)、设防地震(中震)和罕遇地震(大震)作用下的结构响应，提取气柜结构的基底剪力及顶点位移数据，求得3种加载模式的气柜结构初始刚度Ke，分别为542.61，393.67，233.72 kN/mm，再采用静力弹塑性能力谱法计算气柜结构的顶点位移和基底剪力(具体计算步骤可参照文献[12-13])，结果见表2。

表2 3种加载方式下气柜的静力弹塑性分析结果Tab.2 Results of static elastoplastic analysis for gasholder under three kinds of load

由表2可知：均布加载方式下所得气柜结构的基底剪力最大，基本振型加载方式下所得顶点位移最大；均布、倒三角形和基本振型加载下大震性能点处位移值分别为1/925、1/742和1/569，满足气柜筒体顶点位移角限值为1/500的规定，即该结构能抵抗8度罕遇地震荷载作用。

2.2 加肋壳体结构动力弹塑性分析

采用增量动力分析法[14]，对气柜加肋壳体结构进行动力弹塑性分析。根据规范选择地震波的3要素(强度、频谱特性、持时)[9]，选出8条地震波，其记录见表3。

表3 选用的8条地震记录Tab.3 Selected 8 seismic records

图2(a)为所选地震记录的动力放大系数β谱，其平均值与标准β谱的对比见图2(b)。由图2(b)可得，所选地震波的β谱在平台段范围内的平均值与标准β谱的最大误差为18.35%(＜20%)，符合选波要求。

图2 选波β谱与标准β谱对比Fig.2 Comparison of selected and standard β spectrum

采用所选的8条地震波分别对气柜结构进行动力时程分析，提取气柜结构的基底剪力及顶点位移数据，计算每条地震波作用下的结构响应[15]：弹性刚度Ke；多遇地震性能点及相应的谱位移Sd1、顶点位移ut1、基底剪力Ve1；罕遇地震性能点及相应的谱位移Sd2、顶点位移ut2、基底剪力Ve2，结果见表4。

表4 8条地震记录的结构响应分析Tab.4 Structural response analysis of 8 seismic records

由表4可见：罕遇地震等级的性能点对应的最大顶点位移为163.26 mm(Friuli_Italy波作用下)，相应位移角为的1/674，满足气柜顶点位移角限值为1/500的规定；通过8条地震波作用下的时程分析，气柜结构均表现出良好的抗震性能。

Friuli_Italy波作用下的气柜结构动力反应见图3。

2.3 加肋壳体结构静力与动力弹塑性分析对比

依据静力和动力弹塑性分析的结果统一绘制能力谱-需求谱曲线，结果见图4。由图4可知，基于基本振型加载方式所得的性能点相应谱位移最大。因此，对于气柜加肋壳体结构的弹塑性简化分析中，可采用基本振型加载方式，据由此得到的气柜顶点位移对罕遇地震下结构的抗震性能进行评估。

3 基于初始应力条件下的弹塑性分析

初始应力的存在，对结构的弹塑性抗震性能有不利的影响。因此，罕遇地震作用下，气柜顶点位移的计算必须考虑设备恒载和活载组合下的初始应力情况。先对与30万m³实例相近的几种气柜结构在恒载和活载的条件下进行静力分析，得出其初始应力；再对气柜结构进行初始应力条件下的弹塑性分析，为顶点位移计算公式的拟合提供依据。

3.1 气柜结构静力分析

依据30万m³气柜结构常用截面尺寸，选取9种不同截面：筒壁厚ts分别取5，6，7 mm，立柱型号按3种常用型钢规格A(HM350×250)、B(HM400×300)和C(HM450×300)选取。考虑自重、设备和积灰荷载，顶盖施加均布压力3 kPa；筒体施加均布内压15 kPa。运用ANSYS软件对气柜结构进行静力分析，9种截面气柜结构的顶盖和筒体的最大应力σmax见表5。顶盖的最大应力平均值为79.88 MPa；筒体最大应力σmax的平均值为75.03 MPa。取该应力平均值作为结构抗震分析的初始应力。

3.2 初始应力条件下多遇地震作用气柜结构的性能分析

初始应力下针对9种气柜结构采用基本振型加载模式按多遇地震等级施加荷载，计算最大顶点位移ue1，结果表明其最大位移点均出现在筒体与顶盖的连接处，位移值见表6。气柜结构均整体处于弹性工作状态。

3.3 初始应力条件下罕遇地震作用气柜结构的性分析

图3 Friuli_Italy波作用下气柜的动力反应Fig.3 Dynamic response of gasholder under the action of Friuli_Italy wave

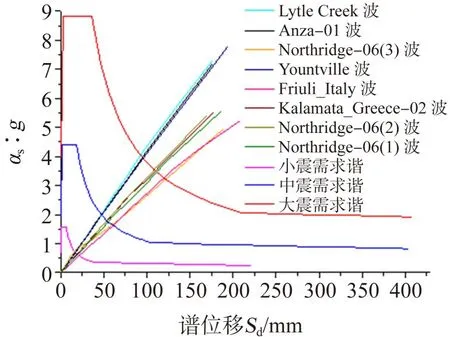
图4 静力与动力分析所得弹塑性能力谱曲线对比Fig.4 Comparison of elastic-plastic capacity spectrum curves between static and dynamic analysis

表5 9种气柜结构的最大应力Tab.5 Maximum stress of 9 gasholder structures

表6 初始应力下多遇地震分析所得最大顶点位移Tab.6 Maximum displacement of frequent earthquake analysis with the initial stress

对气柜结构采用基本振型加载模式按罕遇地震等级施加荷载，底部5 410 mm处应力最大值达到材料屈服强度，进入弹塑性工作状态，见图5。由9种气柜的ANSYS分析结果提取的底部剪力值Vp1略有不同，平均值为40 665.4 kN。

罕遇地震作用下，由9种气柜的ANSYS分析结果可得各种气柜结构的最大顶点位移值up1和位移角θp1见表7。可见：筒体壁厚为5 mm的结构均未达到以气柜筒体顶点位移角限值为1/500作为结构弹塑性分析的性能控制目标。

图5 气柜结构在罕遇地震作用下的应力Fig.5 Stress of gasholder structure under rare earthquake

4 弹塑性分析中气柜结构顶点位移计算公式

表7 初始应力下罕遇地震分析所得最大顶点位移up1和位移角θp1Tab.7 Maximum top displacement and displacement angle under rare earthquake analysis with initial stress

借鉴钢筋混凝土柱承式筒仓的最大弹塑性位移公式的表达形式[10]，针对气柜加肋壳体结构，假定弹塑性分析中结构顶部位移up与弹性分析中顶点位移ue，基底剪力Ve,以及抗剪承载力Vp有关。其中弹性分析中气柜的底部剪力值Ve可取振型分解反应谱法所计算的基底剪力值；抗剪承载力Vp按材料达到屈服阶段时结构横截面所能承担的剪力设计值计算，即

式中：R为筒体半径；ts为筒壁厚度；Az为立柱截面面积；n为立柱数目；fv为钢材的抗剪强度设计值。

4.1 弹性分析中气柜顶点位移ue

鉴于气柜为一悬臂筒体结构，参照悬臂杆件的挠度计算式，采用基本振型加载模式，在初始应力条件下按多遇地震等级进行弹性分析。以由分析所得的气柜顶点位移ue1(见表6)作为公式拟合数据，采用Matlab编程，拟合得弹性分析中的气柜顶点位移ue为

式中：P为基本振型加载下气柜筒体顶部所施加的力；H为筒体高度；E为弹性模量；I为筒体横截面惯性矩。

4.2 弹塑性分析中气柜顶点位移up计算公式

根据表7中初始应力下罕遇地震分析所得气柜顶点位移值up1，以及上述计算所得ue、Vp和Ve的数据，运用Matlab软件编程，拟合得弹塑性分析的气柜顶点位移up计算公式为

为了验证拟合所得计算公式的准确性，另取3种不同高度的气柜筒体截面进行ANSYS有限元弹塑性分析，将所得气柜顶点位移值up,A与由式(3)计算所得up,F值进行对比，结果见表8。可以看出由拟合计算公式计算结果与ANSYS分析结果吻合较好，其误差≤4.2%。

表8 弹塑性分析中顶点位移的ANSYS分析值和计算公式计算值对比Tab.8 Comparison of to pd is placement between ANSYS esults and formula values with elastic-plastic analysis

5 结 论

1)采取均布加载、倒三角形加载和基本振型加载3种加载模式，用能力谱法对气柜加肋壳体结构进行静力弹塑性分析，所得的最大顶点位移均满足顶点位移角限值为1/500的性能目标要求。

2)根据选波三要素选择8条地震波，采用增量动力分析法对气柜加肋壳体结构进行动力弹塑性分析，所得最大顶点位移值满足性能目标要求。

3)基于基本振型加载方式所得的性能点相应谱位移最大，可采用该加载方式对罕遇地震下气柜结构的抗震弹塑性性能进行评估。

4)初始应力条件下采用基本振型加载模式，按多遇地震等级施加荷载，气柜加肋壳体结构整体仍处于弹性工作状态；按罕遇地震等级施加荷载，筒体壁厚为5 mm的结构均未达到结构弹塑性分析的性能控制目标。

5)以弹性分析中所得气柜结构顶点位移计算公式(2)和基底剪力值以及结构的抗剪承载力构建的计算公式(3)可以用来估算罕遇地震作用下气柜加肋壳体结构的弹塑性分析中的顶点位移。