例谈APOS理论指导下的儿童数学“问题解决”能力的培养
——《三角形的内角和》为例
2018-11-01江苏省常熟市石梅小学
江苏省常熟市石梅小学 陆 瑜
近年来,数学素养的培养被数学教育界积极提倡。数学素养通常是在人们与周围环境产生相互作用时所表现出来的思考方式和解决问题的策略。而人们所遇到的问题可以是数学问题,也可能不是明显的和直接的数学问题,从数学的角度看待问题,用数学的思维方法思考问题,用数学的方法解决问题是具备数学素养的良好表现。可以说,培养学习者“问题解决”的能力,是提升数学素养中的重要部分!
一、意义解读:APOS理论下儿童问题解决能力的挖掘
美国的杜宾斯基等人在数学教育研究实践中提出了APOS理论,这一建构过程要经历以下四个阶段:
Action(活动)阶段是指学生参与活动,亲身体验、感受直观的问题背景和各个概念之间的联系。
Process(过程)阶段是指学生对“活动”进行思考,抽象出概念所特有的性质。
Object(对象)阶段是通过前面的抽象认识到概念的本质。
Stcheme(图式)阶段是指建立起与其他概念、规则、图形等的联系,形成综合的心理图式。
APOS理论它特有的数学内容,对教师提升儿童“问题解决”的能力给出了有力的参考!
二、实践磨砺:APOS理论指导下的儿童数学“问题解决”能力培养的策略
APOS理论指出数学活动是学生认识理解数学的一个必要条件,把数学的形式化逻辑链条,恢复为当初数学家发明创新时火热思考。
(一)Action(活动)中,给予儿童丰满的问题解决的经历
1.问题解决中,儿童体验“问题生成”
“问题”从哪里来?让儿童体验问题的生成是儿童经历数学信息的梳理、甄别、筛选的一个实在过程,这样产生的问题能让儿童更加主动和倍感到鲜活!
(1)儿童体验“问题生成”于数学直觉思维中
直觉思维是人们不受逻辑规则约束直接领悟事物本质的一种思维方式。科学家凯德洛夫明确地说:“没有任何一个创造性行为能离开直觉活动。”
【片段1】
师:谁来指一指这个三角形(锐角三角形)的内角?这两个呢(直角、钝角三角形)?
师:三角形的三个内角里隐藏着什么奥秘呢?大家想不想来研究?(想)
师:你觉得我们从哪种三角形开始研究比较容易?
生:有直角的三角形。
师:好的,那我们就来试一试。
虽然学生还没有学习三角形的分类,但直觉认为从“含有直角的三角形”开始研究会容易些。教师对合理成分及时鼓励,利用好这种自发性直觉思维,能让儿童对自己的直觉更加自信,有利于儿童对数学问题的整体感知和问题的生成。
(2)儿童体验“问题生成”于经验的唤醒中
【片段2】
师:这是我们身边常用的三角尺,这把三角尺的内角分别是几度?内角和是多少?(90°+45°+45°=180°)
师:(出示:大三角尺)那这把呢?这两把三角尺形状相同,大小不同,内角和呢?
三角尺大小不同,但内角和没变。强烈的视觉对比,给学生带来内在认识的撞击,从已有的知识经验出发,让学生惊觉问题生成在了熟悉的知识点中,找到了问题的出处。
(3)儿童体验“问题生成”于现象的归纳中
【片段3】
师:再换一把三角尺,它形状变了,内角和呢?(90°+60°+30°=180°)
师:和刚才的两把三角尺内角和相等吗?
师:对这样的现象,你有什么想说的?
生1:大小不同,形状不一样的三角形,内角和都是180°。
生2:含有直角的三角形内角和是180°。
研究三角形内角和,逐步加入了两个变量(大小不同,形状不同),教师启发学生进行了归纳,从多个事件中,找到了共性,提出了猜想,最终形成了一个数学问题。
2.问题解决中,儿童经历“数学思想”的“浸润”
我们提出问题后,如何解决问题是极其重要的部分。而数学思想是解决问题策略的重要依托,是数学知识和方法在更高层次上的抽象与概括。
【片段4】
师:刚才,我们发现三角尺的内角和都是180°。那其他一般的
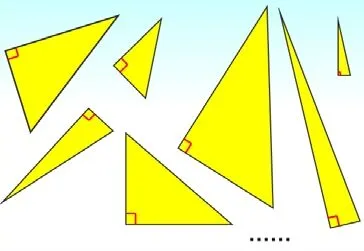
图1

图2
含有直角的三角形(图1),它们的内角和又会是多少呢?
【片段5】
师:含有直角的三角形内角和是180°,那一般的没有直角的三角形的内角和呢?(图2)
在解决问题的过程中,儿童经历的是数学问题思想化的过程,这里学生经历了两次特殊到一般的学习活动,由此及彼,逐步深入研究,分步扩张,完成了数学问题的研究。问题解决过程中,数学思想的浸润是重要的环节,也是解决问题的精髓所在!
3.问题解决中,儿童感受“策略”的“多样”
三角形内角和是180°的验证怎么做?怎样才能让学生真正理解数学问题,螺旋上升为自身的认知结构。这时,策略多样性能让这样的经历更加丰满,体验更加多样。
【片段6】
①操作验证,所见即所得:主要通过量、拼、折、画等方法,进行验证。
②有限验证和无限验证:利用计算机来验证更多的例子。
③演绎推理验证:利用已经研究得到的结论,含有直角三角形的内角和是180度,来论证一般的没有直角的三角形内角和。
这一序列的 Action(活动)中,策略的多样,让学生多了一些探索和讨论,引领着儿童在感受策略的提升和逐步严谨的过程中,走了向数学思维的更高领域。
(二)Process(过程)、Object(对象),成就儿童“问题解决”的能力的蜕变
在Process(过程)、Object(对象)中,致力于让儿童对“活动”进行思考,经历概括内化、过程、反思,抽象出概念所特有的性质,将其“压缩”成为一个思维中的具体对象,在以后的学习中以此为对象去进行新的活动。
1.及时梳理,儿童对单个活动的反思
【片段7】
师:同学们,刚才我们是怎样探索和发现含有直角的三角形内角和是180°的?
生1:我们先发现三角尺的内角和都是180°。
生2:先猜想,一般的含有直角的三角形内角和是180°,再进行验证。
师:是的,现在我们可以说,任意一个含有直角的三角形,内角和都是180°。
2.归纳整理,儿童对多个活动的概括
【片段8】
师:刚才我们发现含有直角的三角形内角和是多少度?(180°),没有直角的三角形,也是?(180°)
师:那三角形的内角和是多少吗?说说你的想法。(180°)
师:(指板书)得出这个结论,我们从特殊到一般,先猜想再验证,想到了好多种方法来探索,学习数学就应该这样!
学生研究了两个板块的问题:(1)含有直角的三角形;(2)没有直角的三角形,这两个板块的内容归结在一起,从研究的板块走向整体的建构。将过程推向对象,即压缩为思维中的具体对象,反思与概括是压缩过程中必不可少的催化剂,同时也能让儿童更好地明确研究问题的步骤与方法,有利于从整体上把握方法与结论。
(三)Stcheme(图式),帮助儿童主动构建心理图式
数学作为一种知识体系,学习者只有将这个新生的“对象”加入到原有的知识结构中,点点相连成线,线线相关成面,才能在头脑中形成综合的心理图式,达到对数学内在本质的认识。
如:将三角形的内角和与长方形的内角和、正方形的内角和,其他多边形的内角和联系在一起,形成网络关系图。
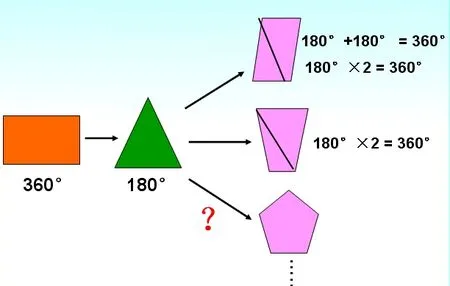
教无定法,教师关注儿童问题解决能力的培养,遵循儿童身心发展规律,依托儿童已有经验,依据有力的教学教育的理论支持,期待教育者带领着儿童去感知和经历这样一个美好的,火热的问题产生、解决、反思的过程!
