基于有向图的天然气冷热电联供系统优化模型
2018-10-31皮硕伟
王 华,皮硕伟
(中国葛洲坝集团装备工业有限公司,武汉 430040)
0 引言
天然气冷热电联供系统是一种建立在能量梯级利用基础上、靠近用户侧的分布式能源系统,可同时完成发电、供冷与供热,其供能方式多样化,综合能源利用率高,是受到广泛认可的天然气清洁高效利用模式[1]。
典型的天然气冷热电联供系统示意图如图1所示,系统通常由燃气发电模块(Power Generation Unit,PGU)(如燃气内燃机、燃气轮机、燃料电池等)、余热回收模块(如余热锅炉、吸收式制冷机等)以及调峰设备(如燃气锅炉、电制冷机等)组成。燃气发电模块通过燃烧天然气发电,同时产生余热,所发电力用于满足电负荷需求,电力不足部分可以由电网补充,多余部分也可向电网出售。通过余热回收装置回收发电模块的余热来满足蒸汽、供暖需求,不足部分可以由燃气锅炉进行补充。余热也可通过吸收式制冷机转化成冷水,用于满足供冷需求,不足部分可以由电制冷机等进行调峰。

图1 CCHP系统示意图
CCHP系统涉及的设备种类较多,各设备特点、效率也不同,冷热电等不同种类之间的能源存在互相转化与耦合,再加上燃料价格、电价、冷价、热价等价格边界条件的不同以及冷热电负荷的波动等诸多因素的存在,导致CCHP系统的复杂性较高[2],因此需要一套有效的数学模型对CCHP系统的设备容量、运行模式等进行分析和优化,进而设计出较好的CCHP系统方案。
1 CCHP系统有向图模型
为了便于建立优化模型,以 CCHP系统的各主要设备为节点,以系统冷热电等能量流动方向为路径,建立CCHP系统的有向图模型,如图2所示。采用有向图模型可以直观有效地表示能量流动的方向与路径,根据各设备的效率及性能系数可以确定节点与节点之间的连接权重,便于写出约束条件与优化目标函数。
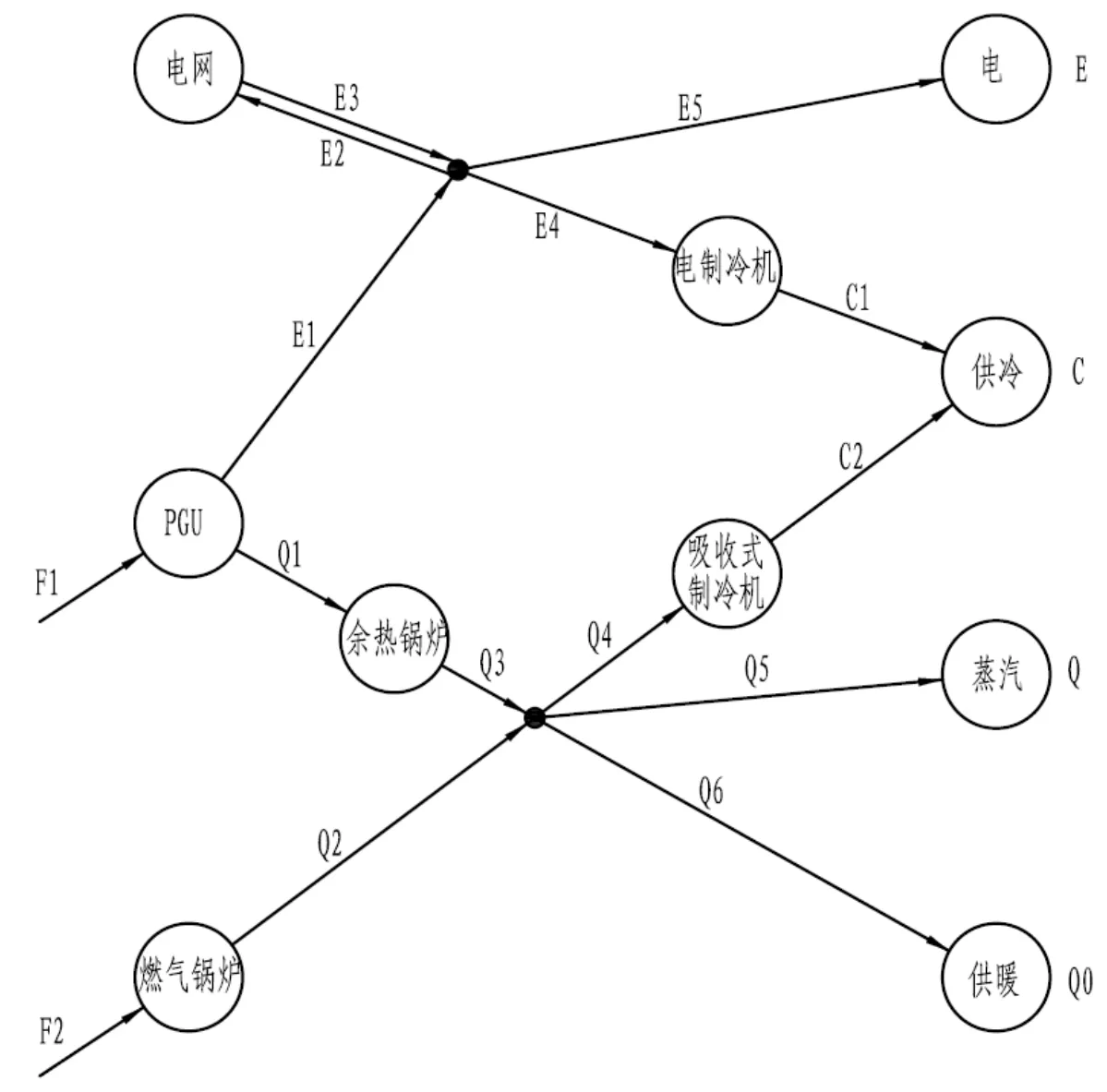
图2 CCHP系统有向图模型
2 最优化模型
2.1 最优化目标函数
理论上,一个精心设计的CCHP系统应该是一个经济效益、节能效益与环保效益综合优化平衡的系统,国内外部分研究在 CCHP系统优化中将经济效益、节能率、碳排放等综合指标作为目标函数进行优化[3]。考虑到目前国内对于碳排放以及节能率优化无明显的激励措施,且目前的国内研究以经济效益为最优化目标[4-5]居多,本文仍以经济效益最优化为目标。
对于并网运行的CCHP系统,在满足用能需求的前提下,优化目标函数为系统总运行成本最小,即PGU与燃气锅炉所消耗燃气成本与净购电成本之和最小,其表达式为
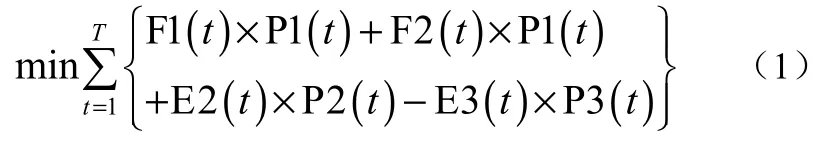
式中:P1为天然气价格,元/(kWh);P2为向电网售电电价,元/(kWh);P3为从电网采购电电价,元/(kWh)。
2.2 约束条件
约束条件包括能量平衡条件、设备自身约束条件、能量转换约束条件和供能约束条件等,结合有向图模型,约束条件的具体表达式如下。
1)能量转换方程

式中:ηe为 PGU 发电效率;ηt为 PGU 余热效率;ηb为燃气锅炉效率;ηh为余热锅炉效率。
2)节点平衡方程

3)制冷转换方程

式中:COPe为电制冷机性能系数;COPa为吸收式制冷机性能系数。
4)负荷约束方程


另外,由于表示真实能量大小,要求模型中所有变量不能为负值。
2.3 模型假定与求解方法
通常CCHP系统中的设备(如PGU、制冷机等)在部分负荷时的效率或者性能系数较满负荷时会有所降低,即ηe是 E1的函数。本文后续算例中使用的JMS416 GS-NL燃气内燃机,其满负荷电效率是41.9%,75%负荷率时电效率是40.6%,50%负荷率时电效率是38.2%。如果将ηe写成E1的函数,优化模型会变成非线性模型,求解较为复杂,并且考虑到效率随负荷率降低的较慢,对求解结果不会有大的影响,假定系统设备在部分负荷时效率保持不变,相关研究文献中也采用了类似的假定[5]。
经过上述假定后,本文所建立的模型中目标函数与约束条件均为线性函数,可以用线性规划进行求解,其数学形式为

式中:A与Aeq分别为不等式约束系数矩阵与等式约束系数矩阵;c为目标函数系数向量;x为优化变量。针对上述模型,本文使用Matlab软件的线性规划求解器求解。
3 算例分析
以某机场CCHP系统为例进行分析,其典型负荷及价格边界条件如表 1所示。模型中所需参数如表 2所示。

表1 负荷与价格边界条件表
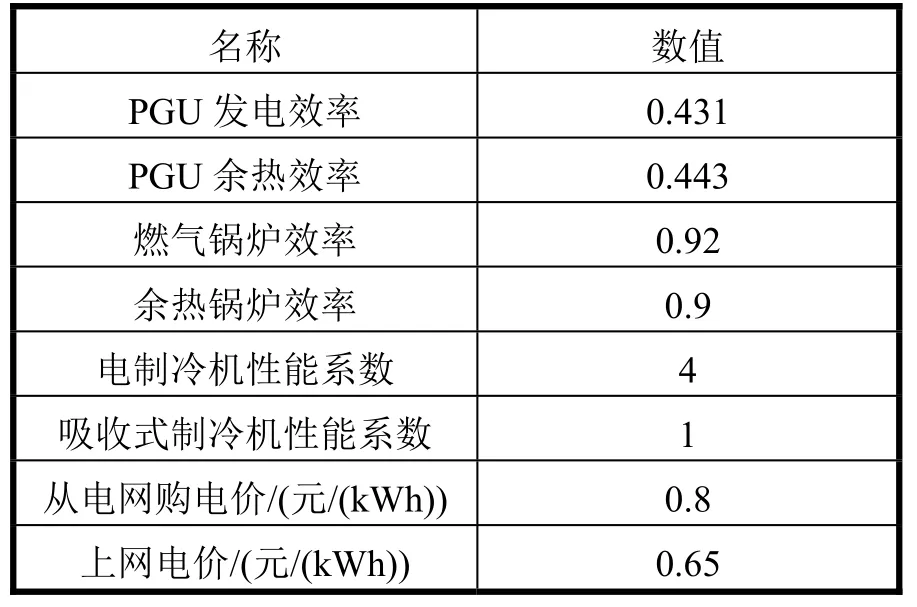
表2 模型参数表
使用基于燃气内燃机的CCHP系统发电,电能供机场使用,多余部分上网。使用烟气热水型溴化锂机组进行余热回收。使用燃气锅炉与电制冷机进行调峰,满足供暖与供热需求。以各设备出力、转换设备的输入、电网购电量等为优化目标,根据第 2节建立的数学模型,将表1、表2中的数据代入,在Matlab中进行求解(注意供暖季运行时冷负荷为0,供冷季运行时暖负荷为0),供暖季优化计算代码如图3所示,后续优化代码类似,不另行列出,运行结果如表3所示。
由计算结果可知:在不加其他约束与限制的情况下,模型优化的结果是使用PGU发电和余热满足全部冷热电负荷需求,无需使用燃气锅炉与电制冷机调峰,也无需从电网购电。由于PGU装机容量较大,余电上网量较多,在此配置下运行时,运行成本为负值,说明向电网售电收益已经高于所消耗的天然气费用,项目能做到盈利最大化。
在实际执行项目时,使用无约束优化模型的计算结果只能作为参考。受到国家与地方政策、余电上网比例、原动机功率大小等限制,一般需结合实际情况选定PGU的规格,在本算例项目中,实际使用了2台JMS416 GS-NL燃气内燃机作为原动机,单台功率为1 200 kW,在选定PGU功率后,需要对CCHP系统的其他设备配置进行优化求解,此时只需在模型中加入如式15所示的约束条件,然后对增加约束后的模型进行求解,运行结果如表4所示。


图3 无多余约束供暖季优化计算代码
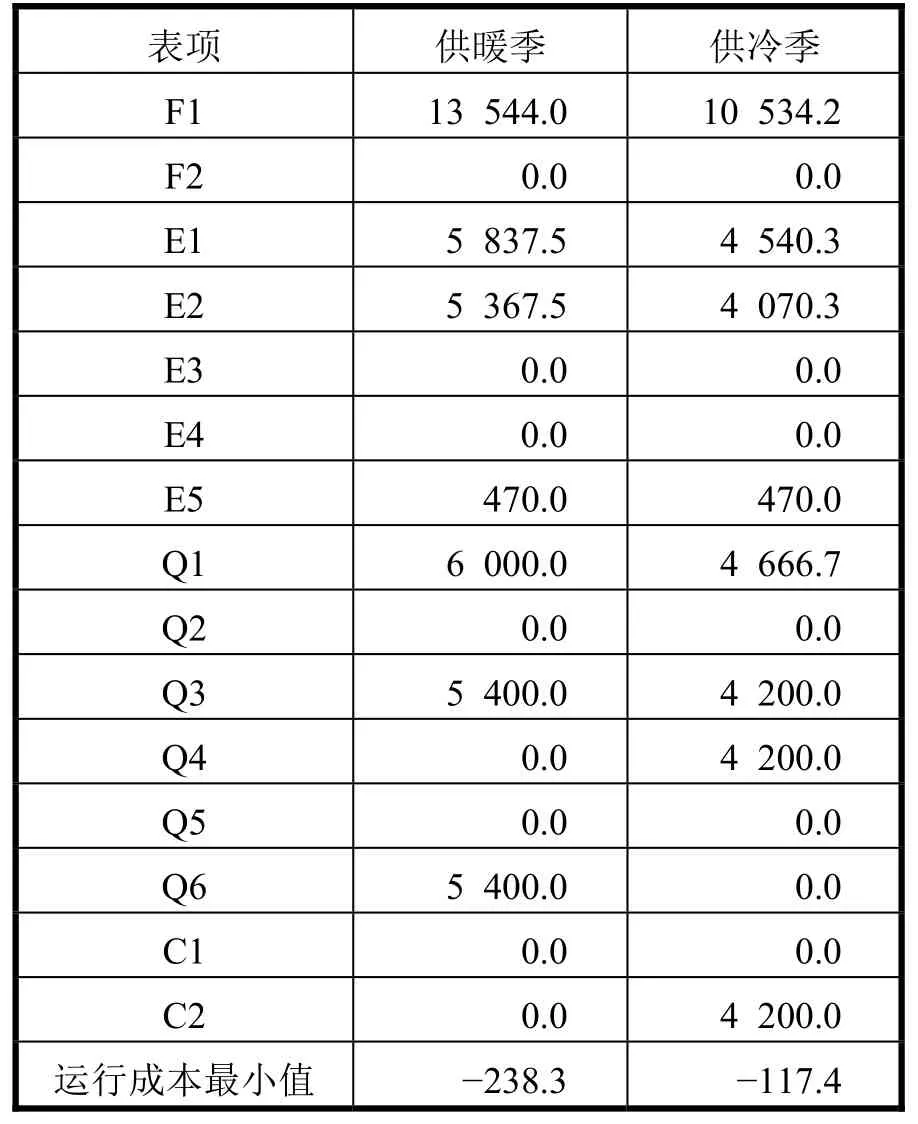
表3 无其他约束条件优化结果

表4 限定PGU功率后优化结果
根据计算结果可以看出:
1)从运行成本最小值结果来看,无约束优化模型得到的运行成本要小于带约束优化的运行成本,改变配置确实引起了运行成本的增加,这说明了优化模型的有效性;
2)在限制了 PGU功率之后,此时余热已无法完全满足供暖与供冷需求,模型自动配置了补燃锅炉(F2)与电制冷机(E4)进行调峰,相应的设备配置容量可以参考F2与E4值选取,另外,除去电负荷与电制冷机用电之外的余电可向电网销售,以得到最大的经济效益,这说明了优化模型的合理性。
4 结束语
本文通过分析CCHP系统中的能量流动转换路径与方向,建立了以各设备为节点的 CCHP系统的有向图模型,并在此基础上提出了 CCHP系统设备配置与运行策略的最优化模型,通过对模型的线性化,将优化模型转化为线性规划问题进行求解。
通过模型对实际案例的测算,将负荷在较长时间尺度下分为供冷季负荷与供暖季负荷,分别在不限制PGU功率和限制PGU功率情况下对CCHP系统进行设备选型与配置优化计算,计算结果均在满足冷热电负荷的前提下达到了最小化运行成本的要求,实现了运行收益的最大化,这为CCHP的主要设备选型与配置优化提供了理论依据,具有实践指导意义。
在 CCHP主要设备配置确定后,可在细时间尺度上进行优化。配合分时负荷、分时电价、分时气价等边界条件,对模型中的优化目标函数与约束条件进行相应更改,调用优化模型计算后即可得到分时时间尺度上的优化结果,如各设备的分时最优负荷率等。实际上,这就是CCHP系统的分时运行策略,分时运行策略优化结果对于CCHP运行控制系统的算法设计与控制逻辑都具有重要意义。
为了扩展模型的适用性,在有向图的基础上,还可以加入储能(储电、储热、蓄冷)节点、新能源节点(光伏、风电)等。另一方面,本文建立的有向图优化模型对于线性或者非线性系统均适用,为了增加模型的精确性,可以不考虑2.3节提出的假定,直接将CCHP系统中设备效率及性能系数写成负荷率的函数,建立起变工况的CCHP系统非线性优化模型,通过非线性求解器[6]或者智能优化算法,如遗传算法、灰色算法等进行求解[7-8],后续将在本文的基础上继续展开相关工作。
