压力型锚杆支护边坡的动力响应与数值分析
2018-10-31张妙芝汪班桥
张妙芝,汪班桥,李 楠
(1.陕西铁路工程职业技术学院,陕西 渭南 714000;2.长安大学,陕西 西安 710054)
边坡在地震作用下的研究一直是岩土工程界十分关心的内容之一。尤其近些年来,地震灾害频发,由地震引发的边(滑)坡失稳案例不断涌现[1]。为了保证地震区边(滑)坡的安全,研究适合边(滑)坡的各种支挡结构就具有重要的意义。锚杆支护边(滑)坡具有施工方便、快捷、安全和经济等特点,是边坡工程中一种主要的支护方式[2]。汶川地震边坡工程调研发现,锚杆支护的边坡一般仅存在局部破坏,具有较好的抗震效果[3]。
目前,对边坡的动力分析主要采用模型试验和数值模拟两种方法。徐光兴等[4-5]采用1∶10的大型振动台试验结合数值模拟研究了边坡的动力特性和地震参数对边坡动力响应的影响。叶海林等[6-8]先后通过FLAC3D软件和振动台试验分别研究了锚杆支护参数对岩质边坡加固效果的影响、边坡锚杆轴力动力受力过程及岩质边坡的破坏特征。赖杰等[9]通过数值分析研究了预应力锚索支护岩质边坡的动力特性。以上研究对象主要是针对岩质边坡和拉力型锚杆,而对压力型锚杆支护土质边坡的动力响应需进一步研究。因此,本文将通过模型试验和数值分析对压力型锚杆支护土质边坡的动力响应进行研究。
1 振动台模型试验准备
振动台试验在西安建筑科技大学结构工程与抗震教育部重点实验室进行,振动台台面尺寸为4.1 m×4.1 m,最大负荷量20 t;最大位移:X向为±15 cm,Y向为±25 cm,Z向为±10 cm;最大速度:X向为±100 cm/s,Y向为±125 cm/s,Z向为±80 cm/s;最大加速度:X向为±1.5g,Y、Z向为±1.0g,工作频率范围:0.1~50 Hz。
1.1 相似关系设计
模型与原型边坡相似比为1∶7,模型试验模拟一高为7 m、坡角60°的原型边坡;相似关系依据重力相似律及量纲分析法推导,选取几何尺寸、加速度及密度作为基本控制量,几何比尺1∶7,重力加速度1∶1,密度1∶1,其他参数通过这三项进行推导,相似关系如表1所示。
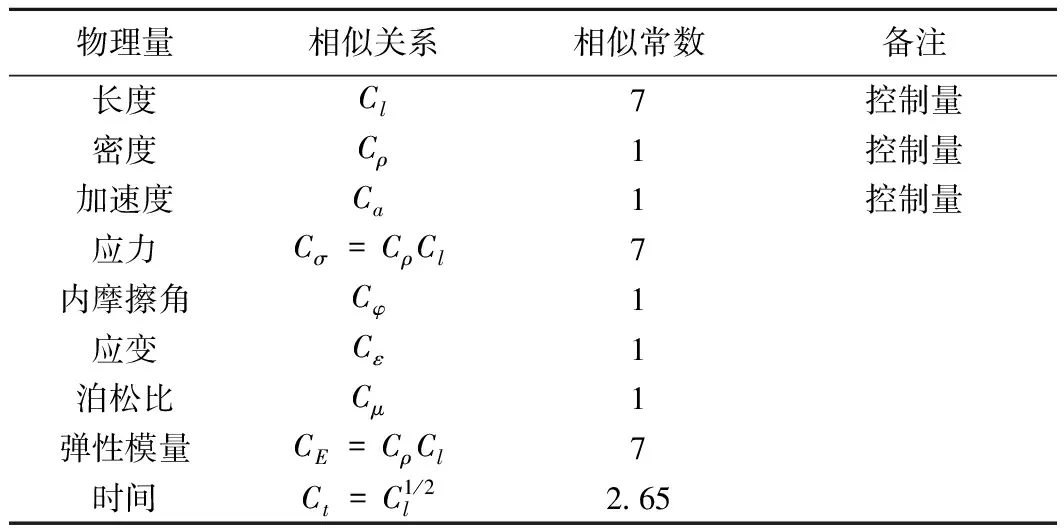
表1 模型试验相似关系Table 1 Similarity relationship of model test
1.2 相似材料与模型制作
试验模型箱由角钢和有机玻璃组成。制作模型时,在模型箱两侧的有机玻璃上涂抹一层凡士林,以减小模型与有机玻璃之间的摩擦;在模型箱底部用环氧树脂黏上一层平均粒径为9 mm的碎石,使之成为粗糙面,以减少土体的相对位移;在模型箱前后两端放置50 mm厚的聚乙烯泡沫作为减震层,以减少模型箱边界对入射波的反射。
模型边坡采用单面坡,模型滑床底部长2 050 mm,顶部长500 mm,宽1 500 mm,高1 300 mm;滑体顶部长250 mm,坡角为60°,模型边坡示意图如图1所示;滑床、滑体均采用土料制备,分层填筑夯实,滑床夯实后,削坡预设圆弧形滑面,圆弧的曲率由极限平衡法搜索确定,滑带用厚2~3 mm的干细土模拟,再次分层填筑制作滑体;待边坡模型完成后,在坡体中预留孔径为25 mm锚孔。模型边坡的实际相似材料参数如表2所示。
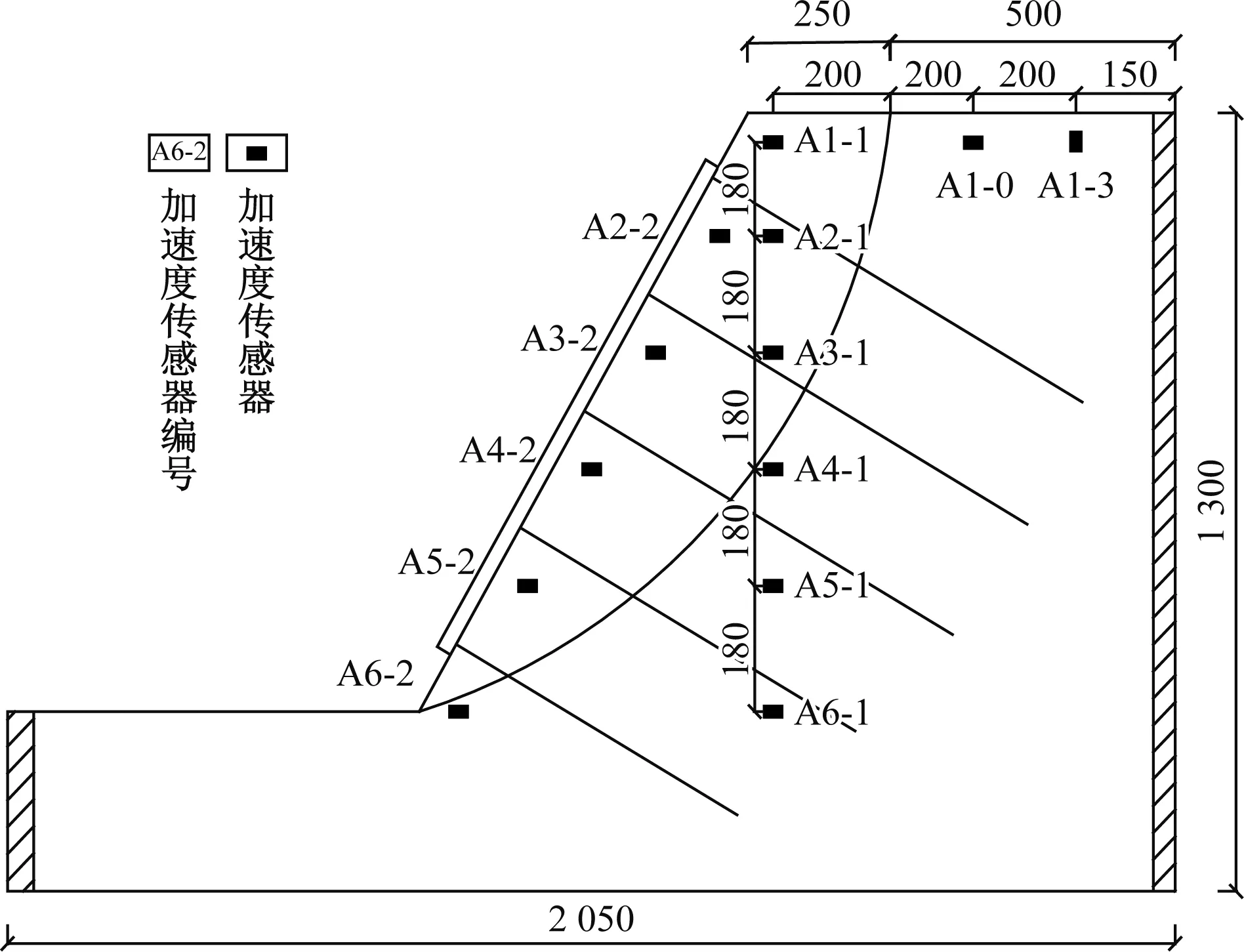
图1 模型边坡断面示意图(单位:mm)Fig.1 Section diagram of model slope(unit:mm)
试验锚杆为压力型锚杆,采用直径6 mm的钢筋模拟全长无黏结锚杆,为了达到全长无黏结效果,在钢筋上涂抹凡士林后缠裹塑料薄膜与砂浆脱黏;设计厚20 mm的Q235钢板圆环模拟锚杆底部的承载体,并用螺帽将其固定;锚孔注浆为现场浇筑,所用砂浆强度为M30;锚杆共5行4列,竖向间距225 mm,水平间距293 mm,锚固段长450 mm,倾角30°;格构框架采用混凝土框架模拟,与锚杆连接。制作完成后模型如图2所示,锚杆的实际相似材料参数如表2所示。

图2 边坡模型Fig.2 Model slope
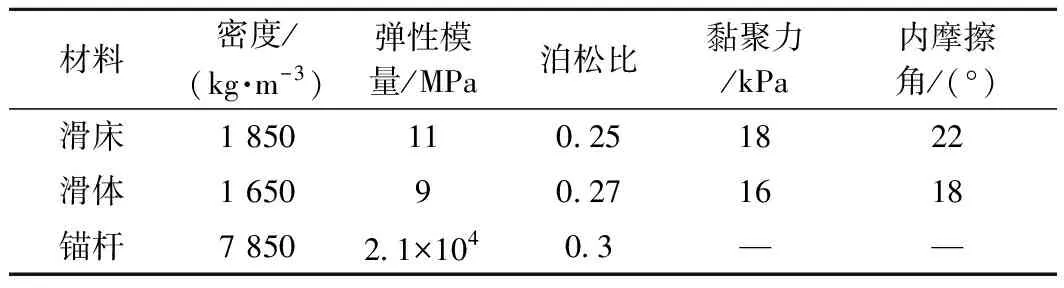
表2 模型材料物理力学参数Table 2 Physical and mechanical parameters of model materials
1.3 试验测点布置
为监测边坡不同高度处的加速度响应,试验在边坡上分别设置12个水平加速度传感器和1个竖向加速度传感器(A1-3),如图1所示;振动试验时在台面上设置2个加速度传感器作为激励控制,控制方式为两点平均控制。在锚杆中选择中间两列进行锚杆轴向应变监测,监测列上的每根锚杆贴有5个应变片(图3)。

图3 应变片布置图(单位:mm)Fig.3 Layout of strain gauges(unit:mm)
1.4 试验加载方案
试验中地震波均采用单向水平输入,选择3种激励波进行:汶川波(2008年,代号W,加速度时程曲线图如图4(a)所示)、EL-Centro波(1940年,代号E,加速度时程曲线图如图4(b)所示)及正弦波(代号Z)。试验采用逐级施加地震量级的方式进行,加载工况见表3。
2 锚杆支护边坡振动台试验结果分析
2.1 模型边坡的动力响应
模型边坡的动力响应一般包括加速度、位移、速度、动应力和应变响应等。地震震害调查表明,与加速度有关的地震惯性力是边坡发生变形和失稳的主要原因[10];目前,规范推荐、工程上应用较多的拟静力法就与加速度的分布规律有关。因此,边坡加速度及其分布规律是评价边坡地震动力响应的基本参数,且其量测容易实施,本文仅对加速度进行研究。为方便研究,文中采用PGA放大系数作为考察指标,其定义是坡体内加速度响应峰值与台面上实测加速度峰值的比值(表3)。

表3 振动台试验加载工况Table 3 Loading condition of shaking table test
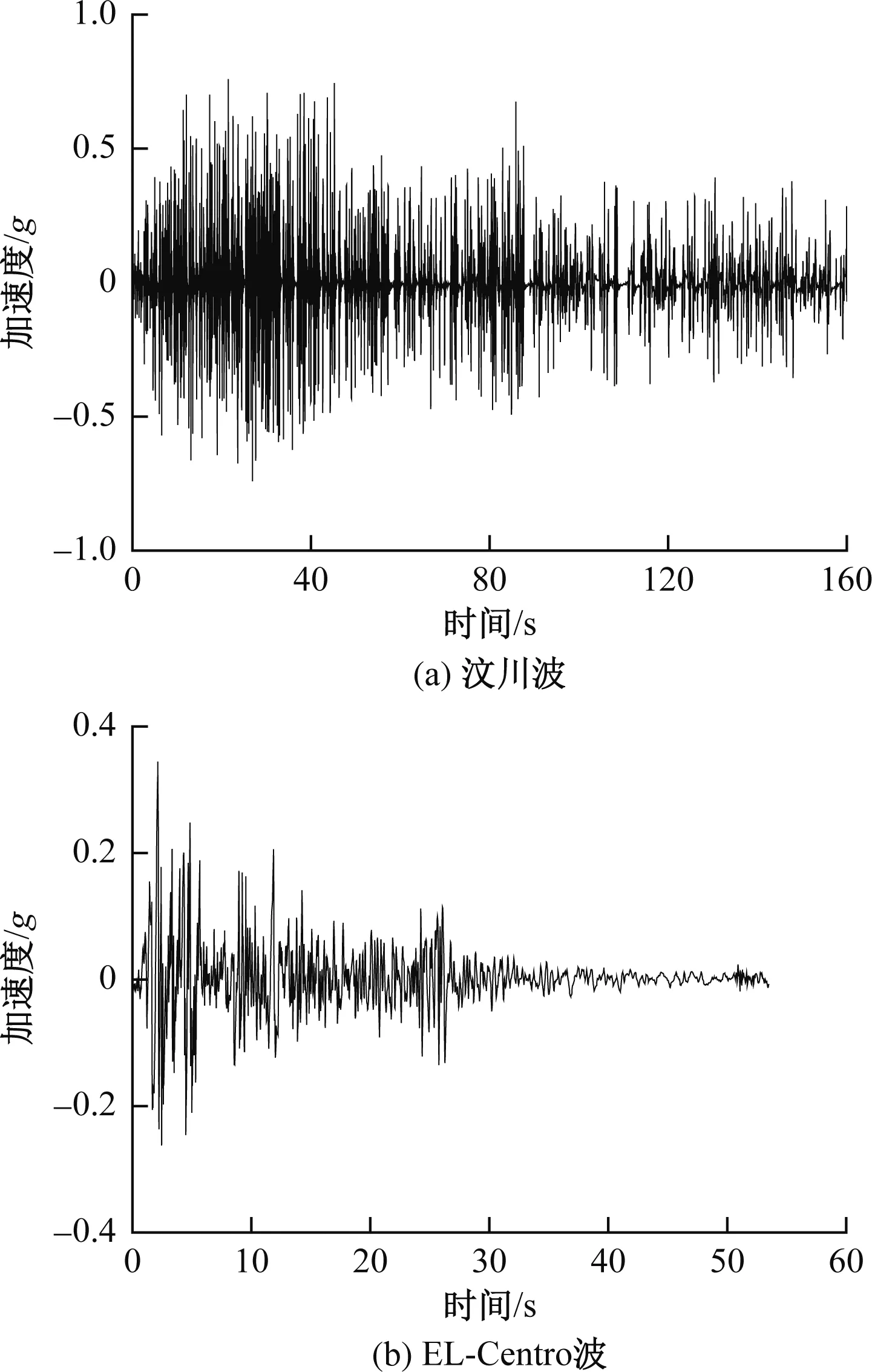
图4 地震波加速度时程曲线图Fig.4 Acceleration time history curve of seismic wave
2.1.1锚固边坡在垂直、水平方向上的加速度响应规律
对模型边坡输入表3所列的各种工况地震波进行分析,发现边坡在垂直方向和水平方向的加速度响应分别具有相似的规律,现以汶川波(W-2、W-5)为例进行阐述。图5给出了坡面和坡体内各监测点的PGA放大系数,从图中可看出,坡体加速度在垂直方向上随高程的增加而增大,到坡顶时到达最大;且各监测点处的PGA放大系数均大于1,说明坡体对地震波起到放大的作用,在坡肩附近最为明显。沿坡体水平方向,坡面与坡内的PGA放大系数走势基本相当,无明显差别,这与徐光兴等[4]研究的无支护边坡水平加速度动力响应结论不同,因本文边坡有锚杆支护,在振动过程中,锚杆格构发挥了作用,加固了滑体,使滑体与滑床形成一个整体,说明锚固力的作用减弱了地震波在坡表反射造成的坡表效应,使坡表坡内的PGA放大系数差别不大。
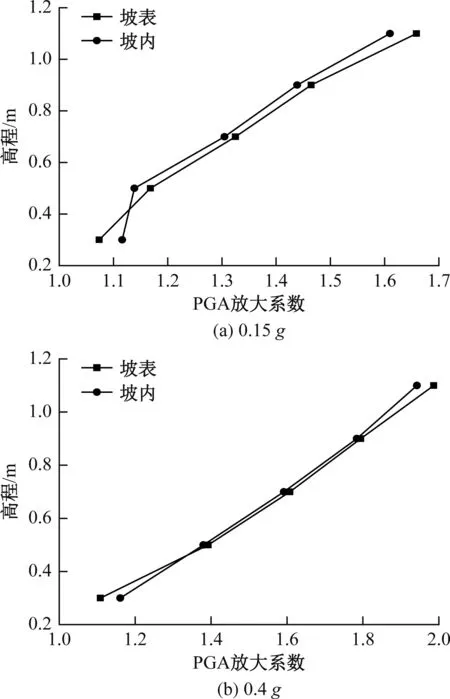
图5 坡面、坡内各监测点PGA放大系数Fig.5 PGA magnification factors of monitoring points in surface and inner slope
2.1.2地震波参数对边坡动力响应的影响
边坡动力响应与边坡所遭受到的地震波密切相关,本文将考虑地震波频率和峰值的影响,以分析边坡在不同频率、不同峰值下的响应规律。以正弦波(Z)为例,图6给出了坡内A1-1、A4-1、A6-1对应监测点处的PGA放大系数,从图中可以看出,在5 Hz时,随着加速度峰值的增大,各监测点处的PGA放大系数整体呈增大的变化趋势,到0.6g时到达最大值;10 Hz时,各监测点处的PGA放大系数随加速度峰值的增大呈现出“先增大后减小”的趋势,在0.2g时到达峰值;15 Hz时,随着加速度峰值的增大而减小;可见,正弦波在低频、高量级,中频、中量级,高频、低量级的激励条件下,对滑坡体的影响较大;也说明了另一个问题:锚固边坡加速度响应不会与地震量级正相关增长,因此,对同一边坡进行抗震支护设计时,应同时考虑地震量级和频率共同作用下的结果。
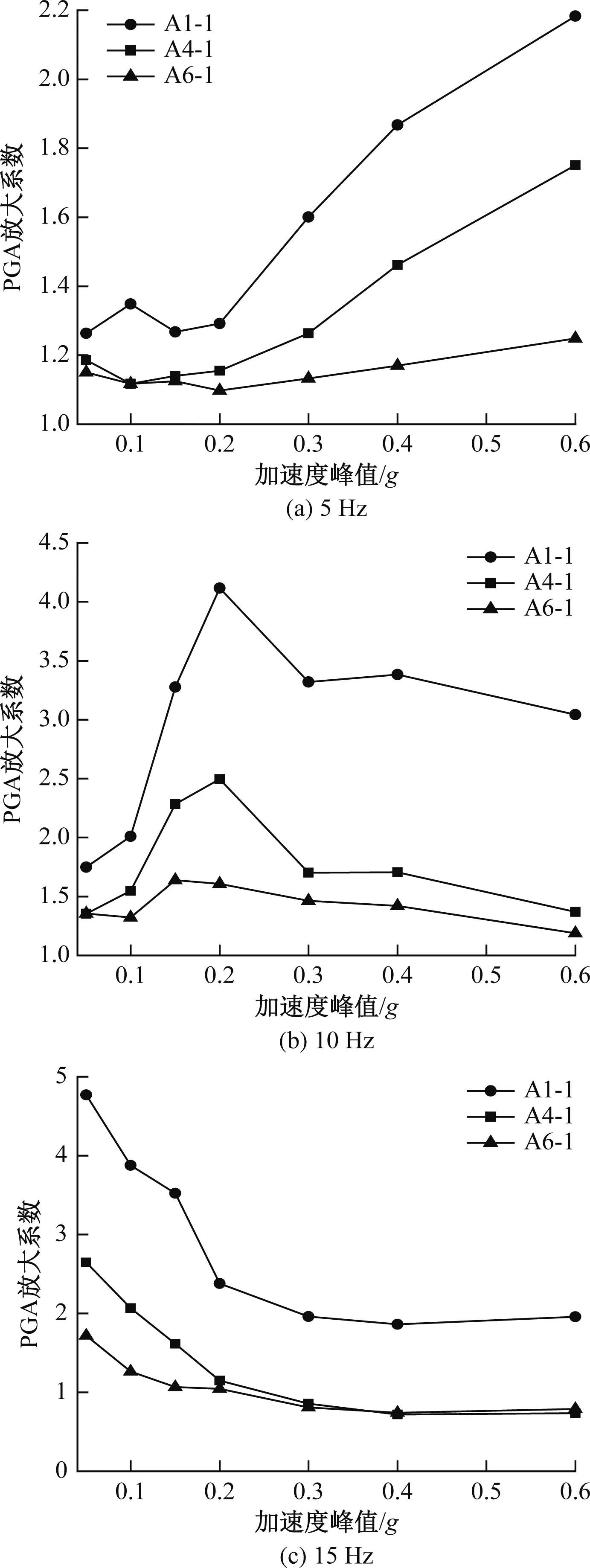
图6 边坡加速度响应随频率、峰值变化曲线Fig.6 PGA magnification factor of slope varies with frequency and peak value
2.2 压力型锚杆应变的动力响应
为研究地震作用下压力型锚杆应变的动力响应,在中间2列的每根锚杆上各设置了5个应变片;现以汶川波为例,研究同一压力型锚杆不同位置处及同列不同高度处锚杆的应变特征。
2.2.1同一锚杆不同位置处的应变特征
图7给出了M3-2锚杆应变沿长度的分布曲线图,可以得出:在0.1g、0.2g加速度幅值下,锚杆应变沿滑面到承载体位置处,呈逐渐递增的趋势,即应变峰值均出现在承载体附近。这是因为压力型锚杆的钢筋与砂浆体之间无黏结,震动过程中外部载荷通过钢筋将力直接传递到底部的承载体,在承载体处产生应力集中,导致承载体附近的锚杆应变较大。在0.6g情况下,坡体稳定系数降低,滑体有下滑趋势,滑面附近锚杆受力较大,所以在滑面处出现较大的应变。
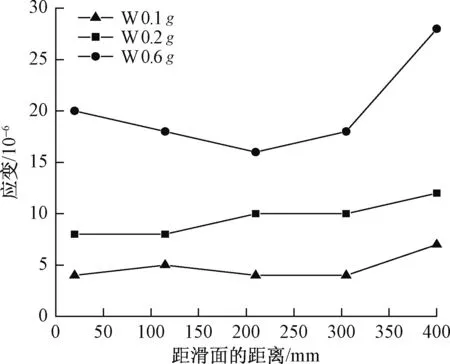
图7 M3-2锚杆应变沿长度分布曲线Fig.7 Strain curves of M3-2 anchor along length
2.2.2同列不同层锚杆的应变特征
本文通过分析第三列各层锚杆滑面处的应变峰值,研究锚杆在不同高度处的动力响应。图8给出了第三列锚杆滑面处测点在不同峰值时的应变曲线,从图中得出:汶川波峰值强度在0.2g范围内时,各层锚杆应变响应不明显;在0.3~0.6g范围内,锚杆应变明显增强,其中顶层、底层锚杆应变尤为突出。说明在强震作用下,坡顶和坡脚处的锚杆承担了大部分荷载,这是因为坡顶滑面处的张拉应力和坡脚滑面处的剪切应力明显增强,为了防止坡体的变形,锚杆发挥了作用。这与传统的边坡设计思想“强腰固脚”不同,顶部锚杆在强震作用下也将受到较大的力。建议在拟静力法设计锚杆加固边坡时,应考虑加大顶层、底层锚杆的轴力。
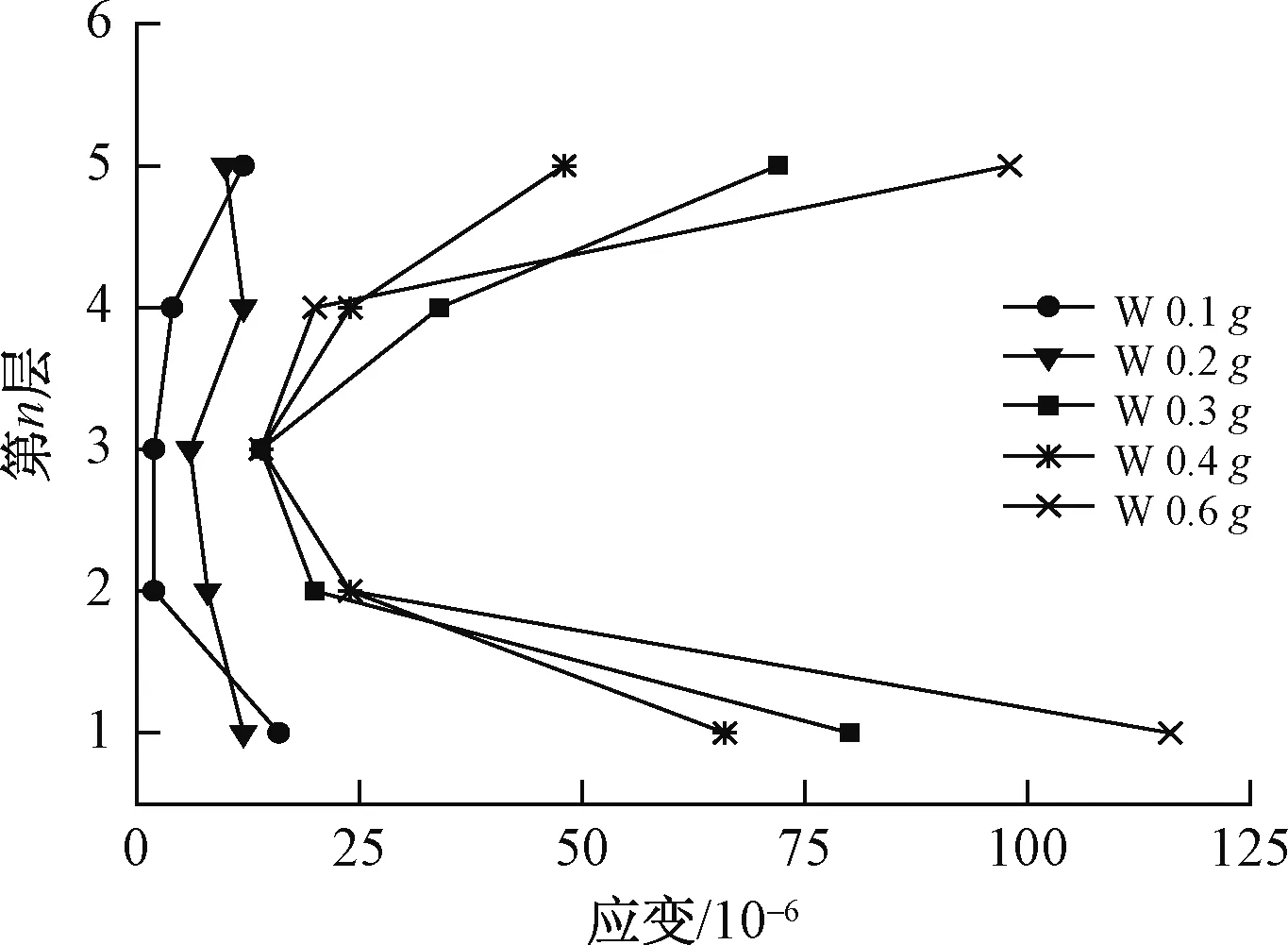
图8 第三列各锚杆滑面处的应变随加载量级的变化曲线Fig.8 Strain curves of anchors at the sliding surface points in the third column varies with loading magnitude
3 锚固边坡模型数值分析
3.1 ABAQUS数值分析条件
本文采用ABAQUS有限元模拟模型锚固边坡振动台试验过程,以分析地震波频率和峰值对边坡动力响应的影响。模型示意图如图1所示,因锚固边坡模型具有对称性,本次数值模拟利用其对称性,截取其中的一半进行计算,建立的数值模型如图9所示;模型材料物理力学参数见表2。数值计算时土体考虑为理想弹塑性材料,屈服准则采用Mohr-Coulomb(M-C)准则,锚杆、砂浆考虑为弹性材料。
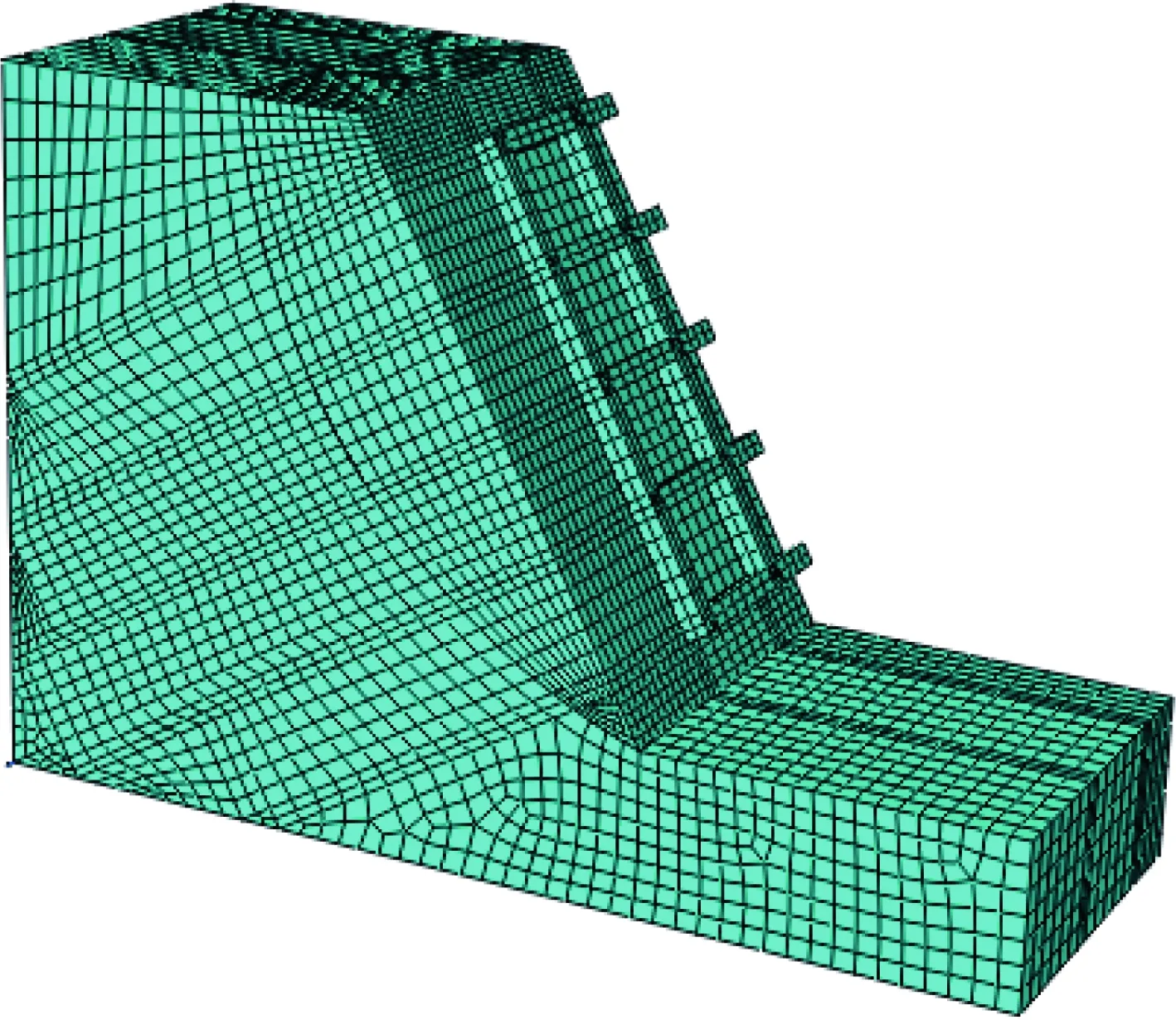
图9 数值模型Fig.9 Numerical model
对于边坡这种半无限体进行动力分析时,需要处理趋于无穷远的边界问题[11],因此文中将边界条件设置为黏弹性边界条件,黏弹性人工边界可以等效为并联的弹簧-阻尼系统[12]。
人工边界法向和切向的弹簧刚度和阻尼系数按照公式(1)和公式(2)取值,其中αN与αT根据参考文献[12]所推荐使用范围并经过数值计算分析分别取1.2和0.7。
(1)
(2)
式中:KBN——弹簧法向刚度;
αN——法向粘弹性人工边界修正系数;
G——介质剪切模量;
R——波源至人工边界距离;
CBN——阻尼器法向阻尼系数;
cp——P波波速;
ρ——介质质量密度;
KBT——弹簧切向刚度;
αT——切向粘弹性人工边界修正系数;
CBT——阻尼器切向阻尼系数;
cs——S波波速。
模拟时先进行静力计算,后进行动力计算。动力计算采用正弦波(Z)进行激励,加速度幅值选用0.1g、0.2g、0.3g、0.4g和0.6g,频率选用5 Hz、10 Hz和15 Hz,边坡加速度监测点的位置与模型试验中的一致,如图1所示。
3.2数值结果分析
数值计算得到A1-1、A4-1和A6-1对应监测点在相同频率、不同加速度峰值下的PGA放大系数,如图10所示。从PGA放大系数来看,模型试验中一个工况下得出的试验结果是前面多个工况试验结果的累积,而数值计算是单一工况下的结果,所以数值计算得到的PGA放大系数稍微偏小些,但总体变化趋势基本一致,即:正弦波在低频、高量级,中频、中量级,高频、低量级的激励条件下,对边坡体的影响较大。
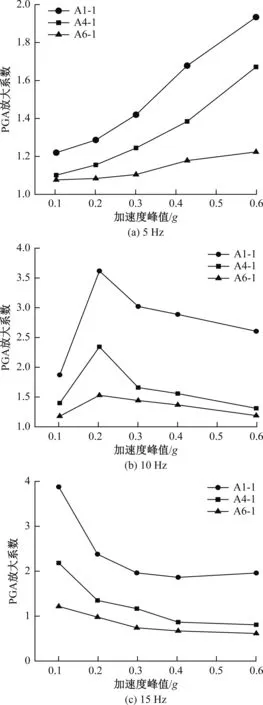
图10 数值计算得到的边坡加速度响应随频率、峰值变化图Fig.10 PGA magnification factor of slope obtained by numerical calculation varies with frequency and peak value
4 结论
采用振动台试验研究了模型锚固边坡、压力型锚杆的动力响应,并通过数值方法模拟了边坡振动台的试验过程,进行对比验证,得出以下结论:
(1)加固边坡土体对输入的地震波有垂直放大的作用,在坡肩附近响应最明显;水平方向放大作用不明显。
(2)在地震频率和峰值共同作用下,边坡加速度响应具有明显的差异,即坡体在低频、高量级,中频、中量级,高频、低量级的激励条件下动力响应较大;建议对同一边坡进行抗震支护设计时,应同时考虑地震量级和频率共同作用下的结果。
(3)在加速度峰值较小的情况下,同一压力型锚杆沿长度方向应变分布呈“前小后大”的模式,在承载体附近应变达到最大值;同列不同层锚杆在垂直方向动力响应差别较大,顶层、底层锚杆应变较边坡中部的锚杆应变响应明显,建议:在拟静力法设计锚杆加固边坡时,应考虑加大顶层、底层锚杆的轴力。
(4)利用ABAQUS数值软件模拟边坡振动台试验过程,得出锚固边坡动力响应特征与振动台试验结果一致,说明了振动台试验结果的合理性和数值分析方法的可靠性。
