三峡库区王家坡滑坡降雨阈值分析

2018-10-31雷德鑫

中国地质灾害与防治学报 2018年5期

雷德鑫，易武

(1.三峡大学湖北省长江三峡滑坡国家野外科学观测研究站，湖北宜昌 443002；2.三峡地区地质灾害与生态环境湖北省创新协同中心，湖北宜昌 443002；3. 三峡大学湖北省防灾减灾重点实验室，湖北宜昌 443002)

滑坡是我国主要的地质灾害类型之一，调查资料显示90%的滑坡由降雨诱发[1-2]。降雨，特别是暴雨或者绵雨对滑坡的稳定性尤为不利，从发生时间上看，三峡库区的滑坡主要发生在每年4～10月的雨季，尤其是6～8月的暴雨季节，滑坡发生的概率以7月最大，占到50%以上。降雨对降雨型滑坡的控制作用主要通过雨水渗透，对滑带岩土体的软化作用，并增大容重，以及由此产生的动水压力和静水压力，使滑坡体抗剪强度降低，最终失稳破坏[3]。滑坡的发生时间不仅与降雨历时、降雨量有关，同时还与降雨强度有关[4-5]。由于降雨入渗、水文水力条件的复杂性、滑坡的非线性动力学特征等使得对降雨型滑坡的预测成为学术界的热点和难点。目前，对降雨型滑坡的预测预报主要有两种思路[6-10]，一种是基于传统的数学统计算法，统计一定区域内滑坡失稳滑动的事件案例，并通过现代专业监测手段提取滑坡发生滑动前的降雨历时、累积降雨量、降雨强度等信息，总结滑坡与降水之间的关系，从而获取诱发区域滑坡的经验性降雨模型。目前，国际上基于统计学建立的经验性滑坡降雨阈值模型大多采用I-D曲线[11]，I(mm/h)为降雨强度，D(h)为有效降雨持续时间，并发展了多种不同的阈值统计关系，其中，降雨强度-历时关系阈值在世界各地降雨预报中使用频率最高[12]。由于经验性降雨阈值不需要严格的数学推导和物理规律，是一种基于宏观滑坡区域和降雨数据的统计模型，且数据客观易得，因此经验性降雨阈值发展比较成熟。另一种是基于降雨入渗机理分析，构建边坡降雨入渗稳定性模型，通过模型试验或数值模拟等手段分析滑坡发生的内在破坏机理[13-15]，由于地下水渗流的复杂性，通常把模型试验和数值模拟相结合，寻求滑坡与降雨的关系，研究发现，降雨强度、降雨历时和雨型对暂态渗流场即边坡稳定性有显著影响。近年来基于逻辑回归统计方法运用到降雨诱发滑坡降雨阈值模型的推导以及滑坡敏感性区划中[16-17]，取得了不错的效果。

本文基于斜率阈值法[18]，分析滑坡累积位移的类破坏点，并选取三个不同观测时段，计算各个类破坏点的累积降雨与观测时段的线性回归系数，最后通过加权平均计算斜率阈值K。

1 斜率阈值法的基本原理

对降雨型滑坡，只有当降雨强度达到一定程度时，滑坡启动并最终失稳破坏，因此，根据降雨预测滑坡的关键是确定滑坡的降雨阈值。本文依据斜率阈值法，分析滑坡累积位移与时间、降雨的关系曲线，分别求取滑坡累积位移的类破坏点、降雨量斜率、斜率阈值等对王家坡滑坡进行定量预报。该预报方法可以分为以下三个步骤：

(1)分析滑坡的累积位移与时间、降雨量的关系，应用斜率单变点求取类破坏点；

(2)对每个类破坏点的前期累计降雨量进行分析综合，得出斜率阈值；

(3)根据实时降雨量求取降雨量斜率，并与斜率阈值进行比较，如果降雨量斜率大于斜率阈值，则滑坡很有可能失稳破坏。

1.1 类破坏点

大量的滑坡监测数据表明：在重力作用下，斜坡岩土体的变形演化曲线具有与岩土体蠕变曲线相似的演化特征，即包括初始变形阶段、等速变形阶段、加速变形阶段、临滑阶段，直至滑坡最终失稳破坏。对降雨型滑坡而言，当降雨达到一定强度时，滑坡变形急剧增大，由等速变形转为加速变形，期间有一个明显的拐点，此拐点称为类破坏点，本文主要通过斜率单变点求取类破坏点，斜率单变点求取步骤如下：

(1)取定探索点。由于监测数据是等时间间隔的，若间隔不等，则用插值的方法预先处理数据，因此选取两个相邻观测时间点的中点为探索点，构成探索点序列ti。

(2)以各探索点为中心构造滑动窗口，以便计算出探索点前、后附近曲线的斜率，即探索点前、后若干数据点的线性回归系数。由于参加回归的数据点数n的大小会影响回归系数的取值，故在探索点前、后各取相同数量(n)数据点构成滑动窗口，以便在相同条件下进行前、后斜率的对比。又由于曲线只有在较短的时间内才近似直线，故n取值不能太大。这里分别取n=2,3,4构成3套滑动窗口。

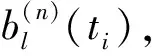
(1)

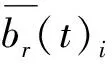
(2)

(5)对ΔS(t)i序列，再计算其二阶差分ΔS2(ti)，即：

ΔS2(ti)=ΔS(ti)-ΔS(ti-1)

(3)

(6)沿着ti从小到大的序列，寻找序列中出现的最大值，设其所在的区间为[ti-1，ti]，它就是斜率变点所在的区间，利用前后相邻的两个区间和及其对应的ΔS2(ti-1)、ΔS2(ti+1)，进行线性内插，即可求得斜率变点的精确值，计算公式如下：

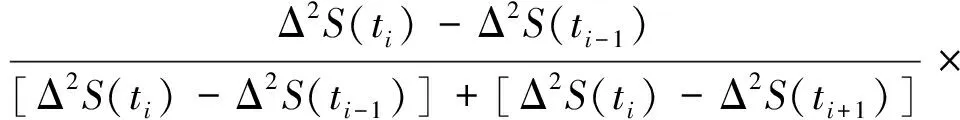
(4)

1.2 斜率阈值

应用斜率单变点求取类破坏点后，再将类破坏点前某一特定时间段n的降雨量累加得到累积降雨量w，并作出各个类破坏点的累积降雨w与观测时段n的关系图，得出每个点的线性回归系数Ki(i=1,2,…，x，x为斜率单变点的个数)，将Ki称为第i个类破坏点的降雨量斜率。将其中一个类破坏点的K值或几个类破坏点的K值得加权平均值定位累积降雨量斜率阈值，简称斜率阈值，即：

(5)

式中，j∈(1,2,…,x),aj为Kj的权值。

2 王家坡滑坡概况

王家坡滑坡位于兴山县城古夫镇古夫河左岸，行政区划属湖北省兴山县古夫镇古洞村1组，滑坡坡体向西倾斜，坡度20°～30°，分布高程225～296 m，主滑方向285°。滑坡平面呈宽舌型，南北宽约170 m，东西纵长约190 m，面积3.23×104m2，平均厚度12 m，体积3.88×105m3(图1)。

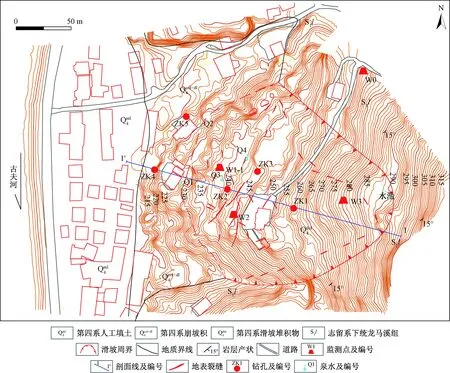
图1 王家坡滑坡平面图Fig.1 Plannar graph of the Wangjiapo Landslide

王家坡滑坡属于土质滑坡，根据滑体物质组成差异，从整体上看可以分为以下两个区域：250 m高程至滑体后缘主要为碎石土，碎石含量较高，土石比3∶7～2∶8，碎块石岩性主要为泥质页岩，棱角状-次棱角状，土主要为粉质黏土，硬塑-可塑。250 m高程至滑坡前缘：上层主要为粉质黏土夹少量碎石，下层主要为碎石土及冲洪积卵石层，碎块石含量相对较少，土石比4∶6～6∶4。下覆基岩岩性为志留系下统龙马溪组(S1l)薄层状泥页岩，岩层产状140°∠15°，坡体结构为逆向坡(图2)。

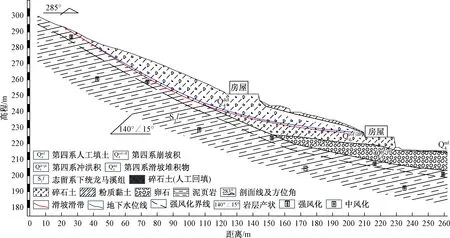
图2 王家坡滑坡1-1’剖面图Fig.2 Sectional view of the Wangjiapo Landslide

目前主要由基准点W0、监测点W1-1、W2、W3组成的自动监测网络以实现对王家坡滑坡位移的实时观测，监测数据表明：自2017年7月8日实施专业监测以来，受降雨影响，王家坡滑坡一直处于缓慢变形阶段，且当降雨达到一定强度时，滑坡变形速率明显增大，而当降雨强度减小时，滑坡变形速率减小，甚至趋于平缓，因此王家坡滑坡属于典型的降雨型滑坡。本文以W2监测点累积位移为例，统计自2017年7月8日监测始，至2017年12月21日止，共计167期监测数据，分析累积位移与降雨量之间的关系(图3)。

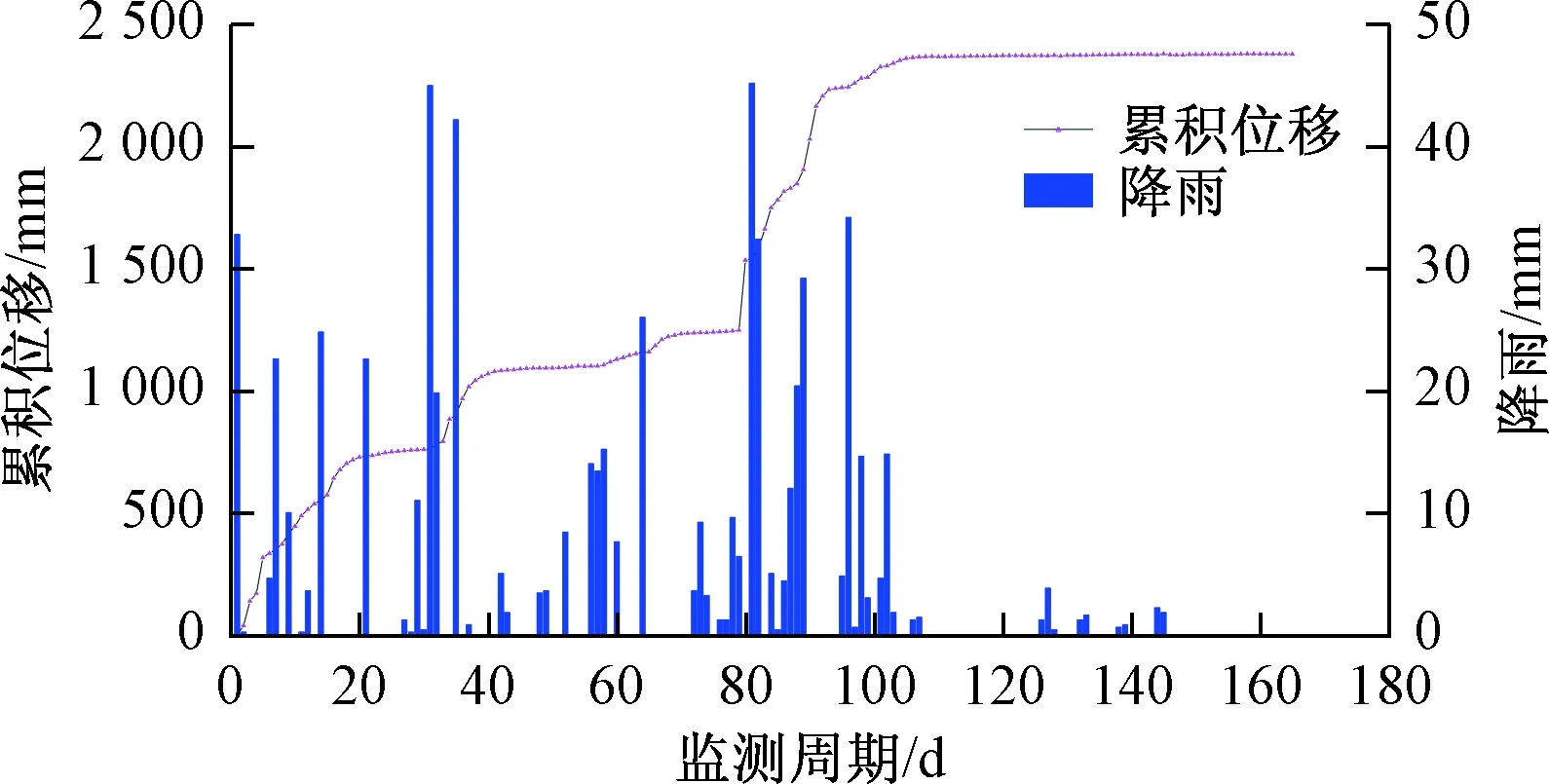
图3 王家坡滑坡累积位移、降雨量关系图Fig.3 The relationship between accumulation displacement and rainfall for the Wangjiapo Landslide

3 求取类破坏点

受降雨影响，王家坡滑坡变形主要集中于前110期，且当降雨强度达到一定强度时，滑坡累积位移曲线发生明显的阶跃现象，因此本文选取前110期监测数据作为研究对象，并分析其类破坏点。由于王家坡滑坡的监测数据是等间隔的，因此选取相邻观测时间的中点为探索点，分别计算探索点前后的线性回归系数及加权平均数，并通过二阶差分确定斜率单变点所在的区间，最后通过线性内插求取斜率单变点的精确值。计算结果显示在t=17，t=37，t=80，t=91处是斜率变点，即滑坡累积位移的类破坏点。

对每个类破坏点分别取观测时段n为2,4,6…14,16，并计算观测时段内的前期累积降雨量w(图4)。结果表明，当观测时段n≤10时，各个类破坏点的前期累积降雨量随观测时段增大而急剧增大，当观测时段n>10时，各个类破坏点的前期累积降雨量增长速率明显放缓，即随时间增加，诱发滑坡的平均降雨强度在降低，总累积降雨量在增大。此外，通过计算各个类破坏点同一观测时段下的平均降雨量，并对不同观测时段下的平均降雨量进行线性拟合，如图4中直线所示，由图4可知，随着观测时段的增长，累积降雨量明显增大，并呈现一定的线性关系。

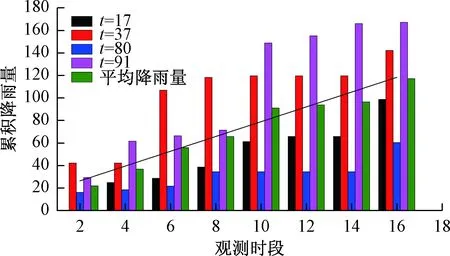
图4 不同观测时段下各个类破坏点前期累积降雨量Fig.4 The accumulation rainfall of each similar failure point under different observation periods

4 降雨量斜率阈值

通过分析统计各个类破坏点的前期降雨量，得出王家坡滑坡的降雨量斜率阈值K，且研究表明：不同的观测时段和时间间隔对降雨量斜率阈值K的影响较大，因此需具体分析讨论不同观测时段和时间间隔条件下降雨量斜率阈值的变化。通过式(6)分析平均累积降雨量斜率：

(6)

式中：Ka——表示平均累积降雨量斜率；

n——观测时段，分析结果见表1。

表1 平均累积降雨量斜率随观测时段、时间间隔变化表Table 1 The change of slope of average accumulated rainfall with observation period and time interval

由表1可知，同一时间间隔下，随着观测时段n的增大，降雨量斜率Ka先增大后减小，同时，同一观测时段下，降雨量斜率Ka随时间间隔d的逐渐增大，整体上呈逐渐减小趋势。分析认为：随时间增加，对于降雨型滑坡，诱发滑坡的平均降雨强度降低，但总累积降雨量在增大，因此，平均累积降雨量斜率随时间增大而呈现先增大后减小的趋势，且前10d累积降雨量越大，滑坡失稳概率越高，因此当n≤10时，滑坡由等速变形进入加速变形阶段时，滑坡累积位移进入类破坏点所需的累积降雨量越大，即降雨量斜率越大；当观测时段继续增大时，在持续降雨作用下，雨水下渗，滑坡岩土体逐渐饱和，物理力学参数明显降低，使滑坡下滑力增大，并最终发生失稳滑动。综合以上分析，随降雨时间的持续增加，诱发滑坡失稳破坏的降雨因素主要为累积降雨量，降雨强度次之，因此，当观测时段持续增加时，平均累积降雨量斜率逐渐减小。不同观测时段下降雨量斜率随时间变化如图5所示。

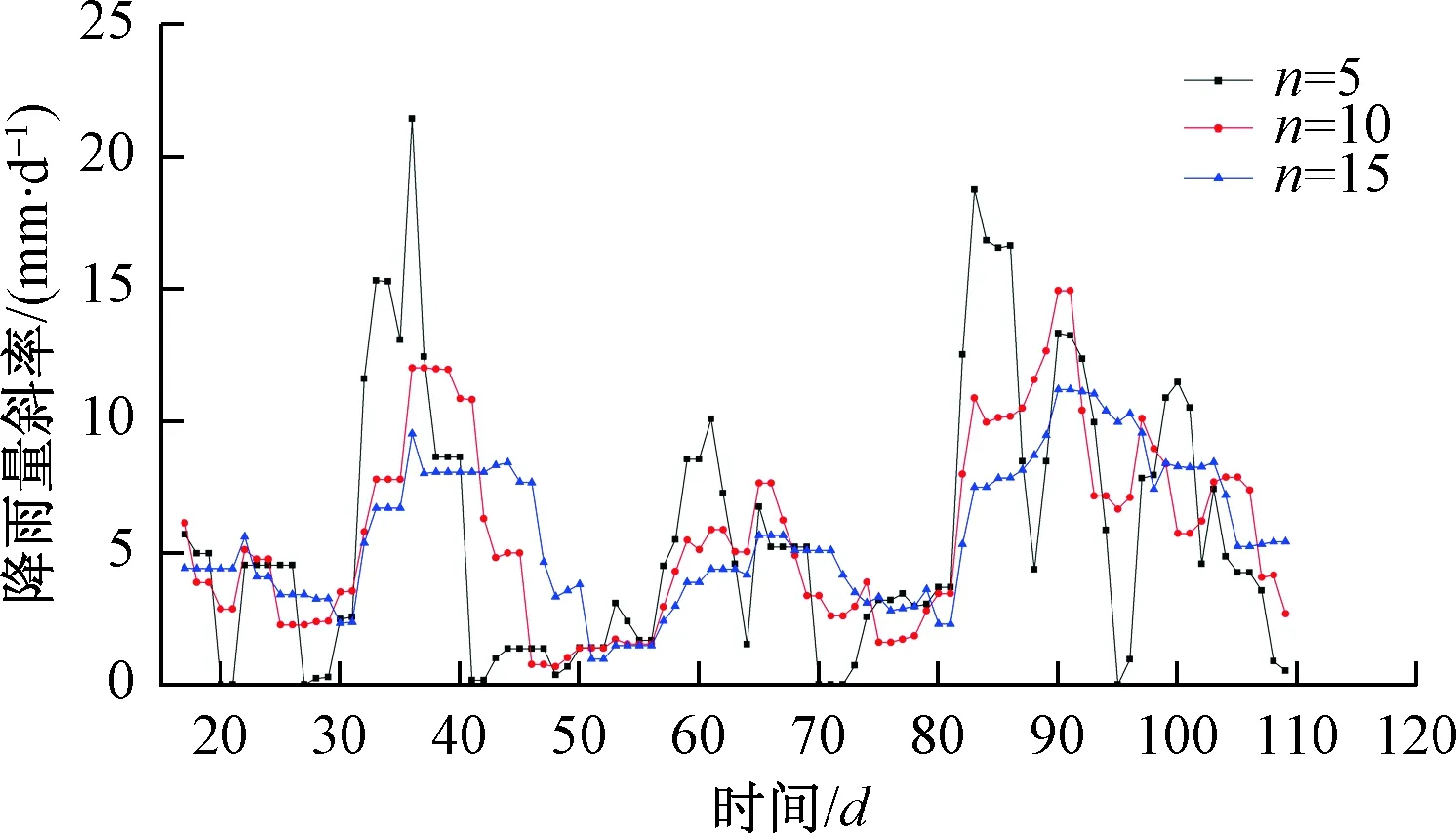
图5 不同观测时段下王家坡滑坡降雨量斜率(d=1)Fig.5 The slope of rainfall under different observation periods (d=1) for the Wangjiapo landslide

5 验证分析

上述研究表明，观测时段与时间间隔是影响降雨量斜率Ka的主要因素，当观测时段n≤5时，此时各个类破坏点的线性回归系数反映局部的斜率性态较多，反映整体的斜率性态较少，又由于点数太少，随机性太强，统计意义不够；相反n≥15时计算得到的回归系数反映整体的斜率性态较多，反映局部的斜率性态较少，又由于点数较多，统计意义较强、随机性较小；n=10则介于两者之间。因此，本文选取n=10，d=1，分别计算各个类破坏点的前期累计降雨量，将其线性回归计算各个类破坏点的降雨量斜率，通过加权平均得降雨量斜率阈值K=10.95。

通过对前110期监测数据进行验证分析，对剩余57期监测数据进行预测预报，并取斜率阈值K与降雨量斜率-时间关系曲线上升段的交点。如图6所示，在前110期监测数据中，t1=37(与实际相差0d)，t2=83(与实际相差3d)，t3=88(与实际相差2d)，验证效果较好。且剩余57期降雨量斜率均接近于0，远小于斜率阈值，表明此段时间降雨量远未达到滑坡临界降雨阈值，即滑坡处于稳定状态，累积位移几乎无变化，结合监测数据，预测效果较好。