西部“三高”地区高速公路边坡稳定性系数与失稳概率关系探讨

司马丹琪,李元松,姜成潼,何 泉

(武汉工程大学土木工程与建筑学院,湖北 武汉 430074)

随着西部大开发与“一带一路”国家发展战略的实施，大批基础设施，尤其是高速公路建设已逐渐向西部高寒、高海拔、高地震烈度(俗称“三高”)地区推进。由此产生的地质灾害问题日益凸现，其中高陡边坡的稳定性问题一直是困扰公路工程勘察、设计、施工乃至运营安全的技术难题。寻求适合“三高”地区快速有效的边坡稳定性评价方法是亟待解决且意义重大的岩土工程技术问题。当前，边坡稳定性评价方法常用的有定性分析法、定量分析法和非确定分析方法三大类[1]，其中在工程地质勘察阶段，应用最为普遍的是极限平衡分析法。但传统的极限平衡分析方法中，计算参数选取往往是采用岩土体试验结果的平均值，没有考虑不确定性因素的影响，与实际情况有所差别[2]。应用基于随机理论的可靠度分析方法是边坡稳定性评价的发展方向[3-4]。然而，目前的工程勘察、设计规范仍然是按整体稳定性系数表征边坡的稳定性，这就存在失稳概率与传统的稳定性系数之间的转换问题[5]。研究表明边坡的失稳概率与岩土体强度参数的变异特性密切相关[6]，岩土体的变异特性又受地质环境条件的影响而具有显著的地区差异性[7]。

拟以G0711乌(乌鲁木齐)尉(尉犁)段高速公路为背景，探讨“三高”地区高速公路边坡可靠性分级标准以及与整体稳定性系数之间的转换关系，为“三高”地区高速公路边坡稳定性快速评价，进而为可靠度方法在边坡工程的实际应用做一些有益的尝试。

1 边坡可靠性分级标准

1.1 边坡稳定性分级

《滑坡防治工程勘查规范》(DZT0218—2006)中将滑坡的稳定状态分为四级(表1)。

《公路路基设计规范》(JTG D30—2015)没有明确划分边坡的稳定性等级，但从相关条款3.7.7可解读为稳定性系数大于1.2表示稳定，1.1～1.2基本稳定，1.0～1.1为潜在不稳定或欠稳定，小于1.0表示不稳定。

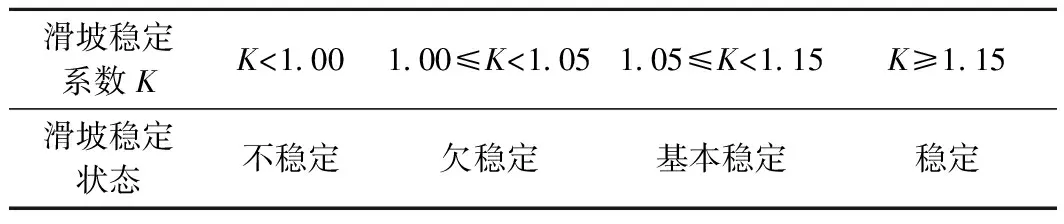
表1 边坡稳定状态划分Table 1 Division of slope stability

考虑到高寒、高海拔、高地震烈度区边坡稳定性较一般地区更为敏感，且工程边坡数量巨大，单项工程治理成本高等因素，在进行稳定性评价时宜在原有分级的基础上进行细分，因此本次研究将边坡稳定性状态分为五级(表2)。

表2 “三高”地区边坡稳定状态划分建议值Table 2 The suggested value of slope stability in the “three high” region

1.2 边坡可靠度分级

关于边坡可靠性分级，规范中没有明确划分，相关研究文献也少见。《公路工程结构可靠度设计统一标准》(GB/T 50283—1999)中有所涉及(表3)，但不完全适用于边坡工程的稳定性分级。

表3 路面结构的目标可靠指标Table 3 Target reliability index of pavement structure

参考GB/T 50283—1999的方法，考虑便于与整体稳定性系数法对应，因此将三高地区公路边坡可靠度分为五级(表4)。

表4 “三高”地区边坡稳定状态可靠性分级Table 4 Classification of slope reliability in “three high” region

2 边坡失稳概率的影响因素

2.1 岩土参数分布类型对失稳概率的影响

实际工程中为便于计算可靠度指标β，往往人为假定岩土体力学参数服从正态分布。研究表明可靠度指标β与岩土体参数变量的分布类型有直接关系，若当参数实际服从非正态分布时，将非正态分布随机变量直接简化成正态分布随机变量，计算所得到的可靠度指标误差达20%～30%[8]。但当参数变量的平均值和变异系数相同，分布类型不同时，可靠度指标和失稳概率的结果有所差异，有分析结果表明，可靠指标β≤3.09(或Pf≥10-3)时，参数分布类型对失稳概率Pf的影响不敏感[9]。边坡稳定评价问题，可靠度指标多数处于β≤3.09范围内，因此，工程应用中，在未知分布类型的条件下，将岩土体强度计算参数视为服从正态分布是可行的。

2.2 参数变异性对边坡失稳概率的影响

对于岩质边坡而言，边坡稳定性虽主要受结构面控制，但假定边坡为均质体，对边坡进行最不利滑动面搜索所得到的边坡稳定性系数亦可作为边坡整体稳定性评价的参考。影响边坡整体稳定性的因素有很多，研究表明坡体容重γ、黏聚力c和内摩擦角φ等参数随机变量的特征明显。

为研究其变异性对可靠度指标β或失稳概率Pf的影响。设计如图3所示算例：某一均质土坡，坡高20 m，坡角45°，黏聚力c为10 kPa，内摩擦角φ为30°，容重γ为20 kN/m3，弹性模量E为14 MPa，泊松比μ为0.3(图1)。

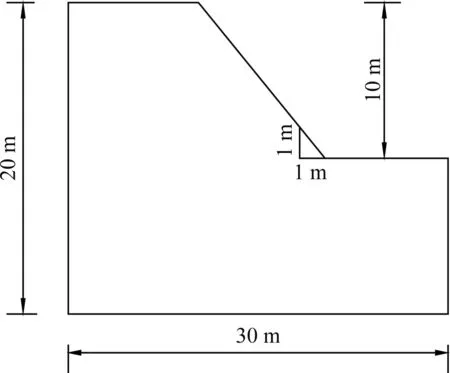
图1 边坡计算模型Fig.1 Computation model of slope

利用GEO-slope中的可靠性分析模块，建立适用于折线滑移面的Morgenstern-Price法极限平衡方程，采用Monte-Carlo随机模拟法求算边坡稳定性系数概率密度分布函数及其失稳概率。变异系数δ与失稳概率Pf之间的关系曲线见图2。

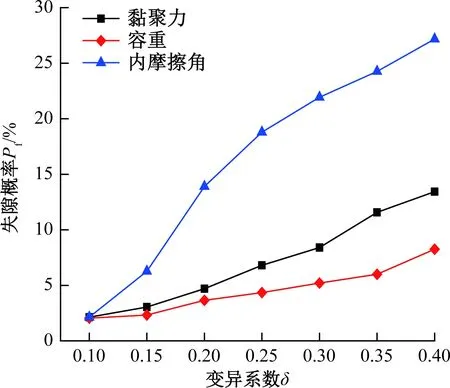
图2 变量γ、c、φ的变异性——失稳概率关系曲线Fig.2 The relation curve of variability of variable γ、c、φ and failure probability

由图2可知，无论哪种随机变量，失稳概率Pf与变异系数δ呈正相关[10]。变异系数一定时，以内摩擦角φ的变异性对边坡稳定性更为敏感，因素敏感性顺序为φ>c>γ，这与范昭平等[11]研究结果一致。因此在可靠性分析之前，根据边坡实际情况，经测试试验与统计分析，准确确定内摩擦角φ的变异系数，对提高边坡稳定性评价结果的可信度至关重要。

3 Pf与K之间对应关系

3.1 边坡稳定性分析模型

以G0711乌(乌鲁木齐)尉(尉犁)段高速公路典型边坡模型为例，研究“三高”地区稳定性系数与边坡失稳概率之间的关系。研究段地层主要为石炭系奇尔古斯套群(C1qr)灰绿色、灰黑色凝灰岩、粉砂岩、泥岩夹砾岩、硬砂岩、长石砂岩、灰岩、火山角砾岩和泥盆系天格尔组(D3tc)葱绿色泥岩、凝灰质硅质岩、凝灰岩、凝灰砂岩及硅质岩、砾岩和(D3tb)凝灰粉砂岩、凝灰砂岩、硅质岩、泥质粉砂岩夹凝灰岩和灰岩透镜体。典型边坡工程地质模型见图3。

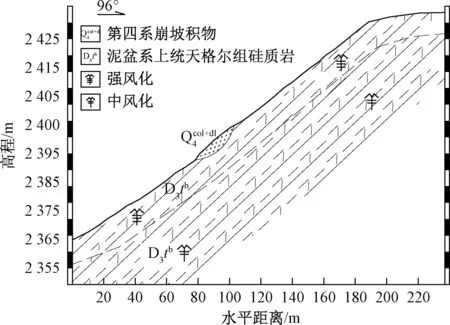
图3 边坡分析简图Fig.3 Schematic analysis diagram of slope

3.2 强度参数统计及检验

根据现场调查与室内外试验，得到边坡岩土体强度参数(表5)。

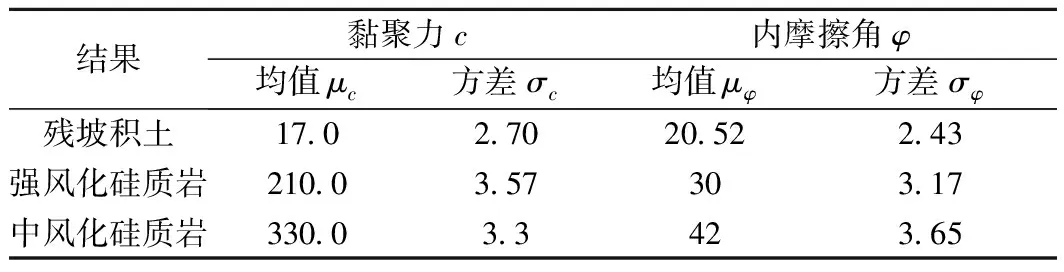
表5 边坡岩土体强度参数统计量Table 5 The random values and statistics of slope

以残坡积土为例，将岩土体黏聚力、内摩擦角数据绘成直方图(图4、图5)。

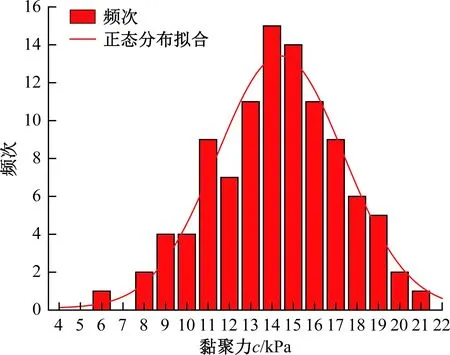
图4 黏聚力参数分布直方图Fig.4 Histogram of cohesive parameters distribution

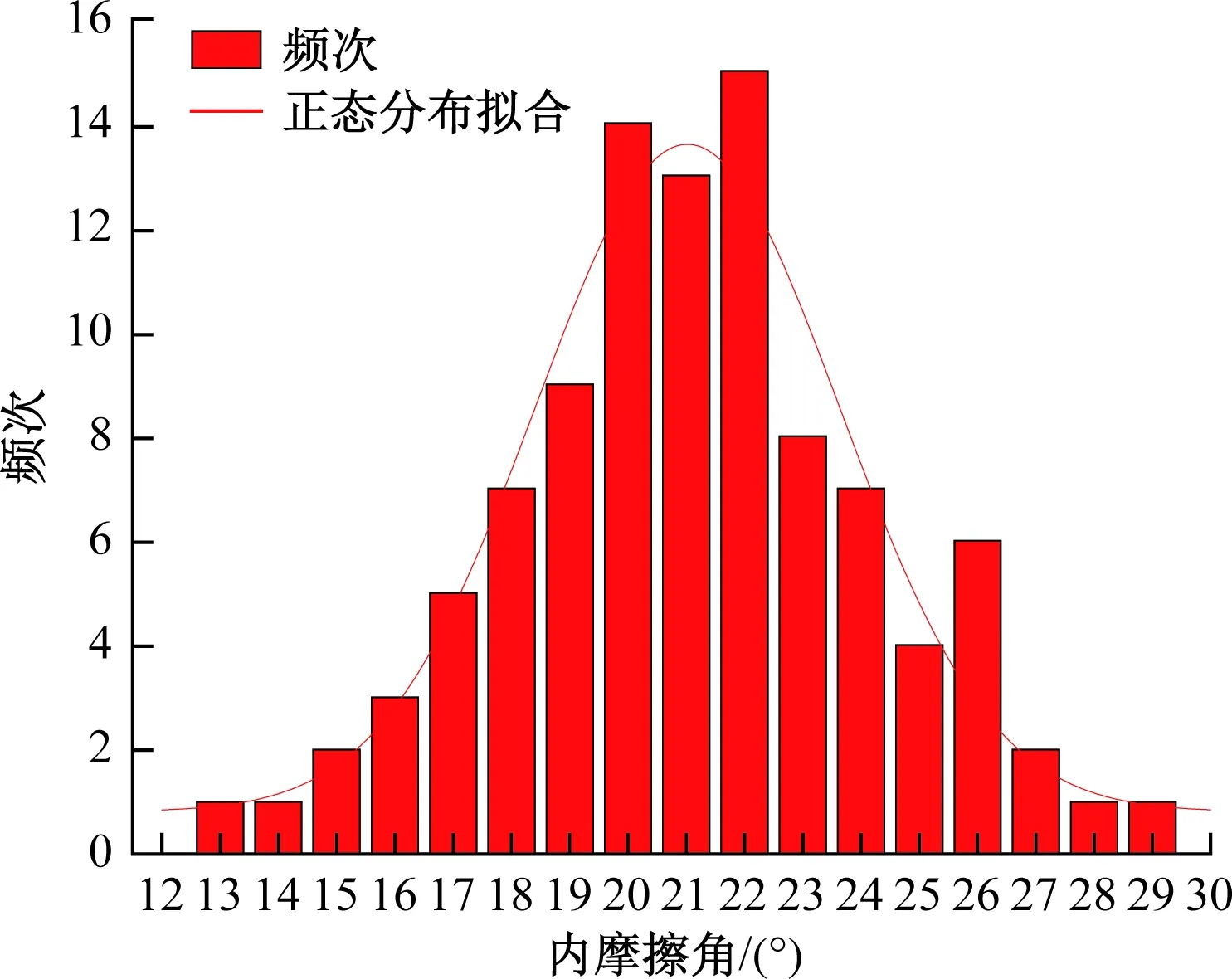
图5 内摩擦角参数分布直方图 Fig.5 Histogram of internal fraction angle parameters distribution

利用K-S假设检验法对岩土体抗剪强度参数概率分布模型进行检验[12-13]。利用统计软件SPSS计算，内摩擦角p(N)=0.649>0.05，黏聚力p(N)=0.904>0.05，说明黏聚力、内摩擦角都服从正态分布。

3.3 Pf与K之间的对应关系

如前3.2节分析，建立可靠性分级与传统稳定性分级之间的对应关系，关键是确定岩土体的强度参数c、φ的变异特性。骆飞等[14]将岩土体强度参数[15]的变异特性分为五个等级，运用幂函数进行回归分析，建立可靠指标β与均值稳定性系数K的三参数函数关系式：K=aiβbi+ci，式中：β的取值范围为β=1.0～3.0，i=1、2、3、4、5分别表示岩土体抗剪强度指标的5种变异等级，ai、bi和ci为对应五种变异等级的回归常数。其思路与方法值得借鉴，但岩土体强度参数取值与变异特性，不适用于“三高”地区。根据现场调查，室内外试验，统计出“三高”地区岩土体力学参数变异范围(表6)。

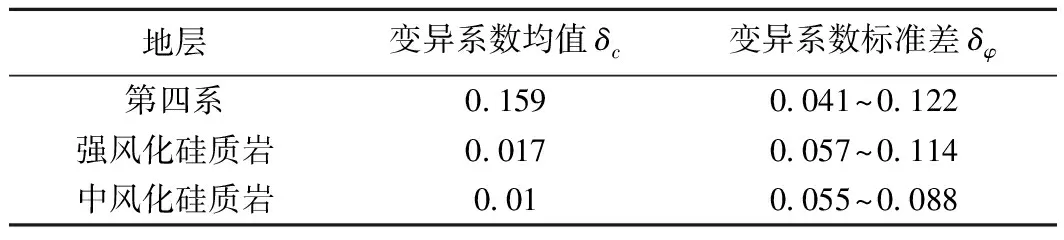
表6 “三高”地区参数变异范围Table 6 The range of parameter variation in “three high” region

根据表6中参数的变异范围，将岩土体强度指标的变异水平划分为5个等级(表7)。

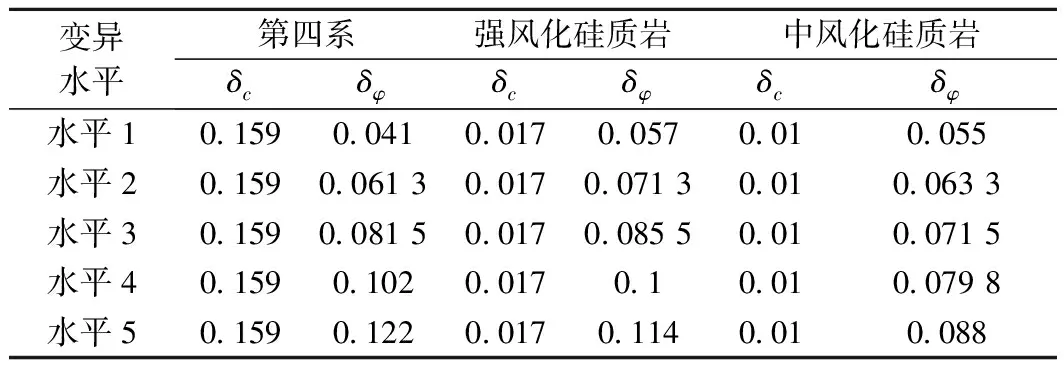
表7 抗剪强度指标变异水平划分Table 7 Variation level of shear strength index

根据表7分级标准，基于Monte-Carlo原理，借助GEO-slope平台，计算整理不同变异水平下失稳概率与稳定性系数的变化规律(图6～图8)。

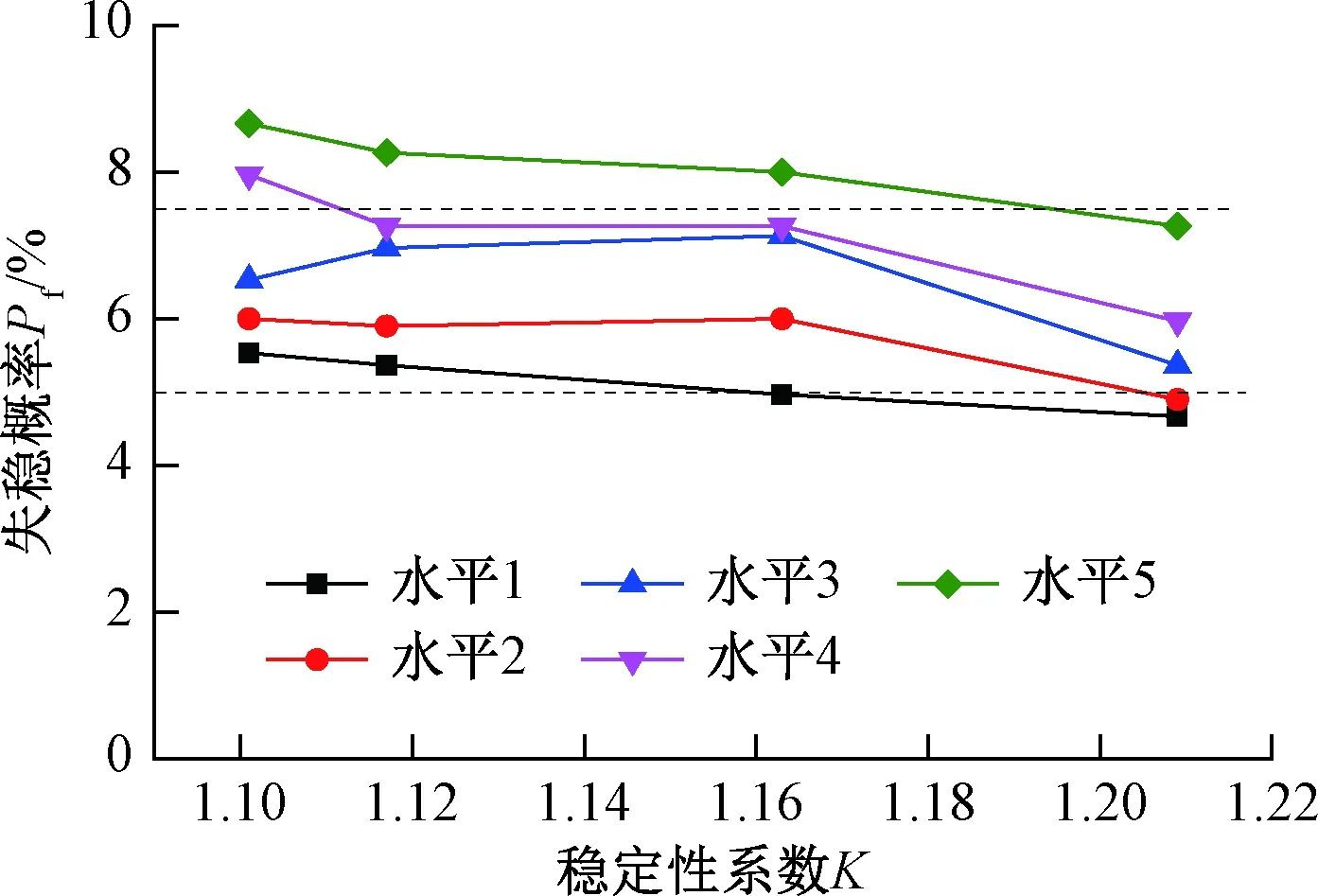
图6 1.1≤K≤1.2时，稳定性系数与失稳概率变化关系Fig.6 Relationship between the stability factor and the failure probability when 1.1≤K≤1.2

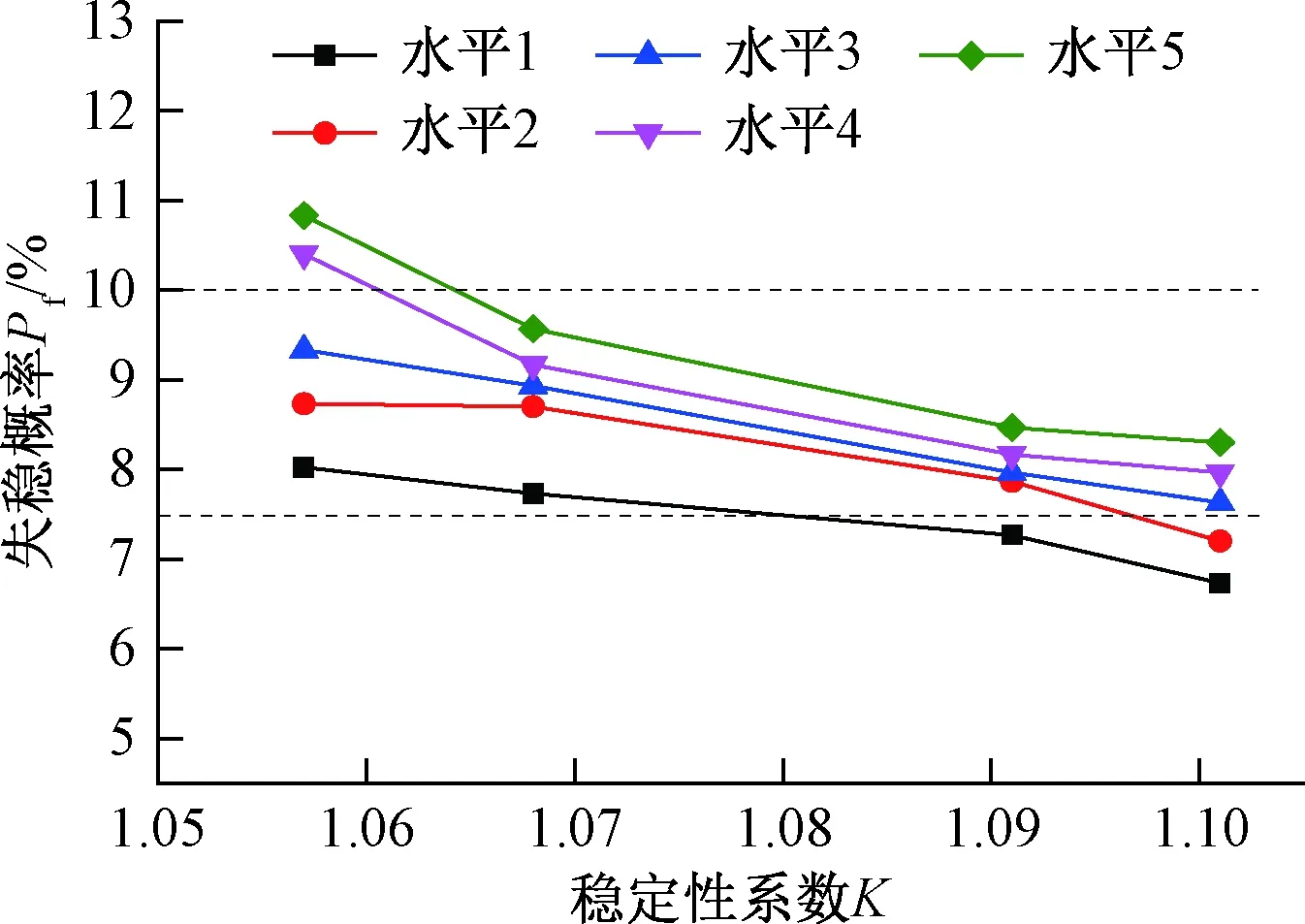
图7 1.05≤K≤1.1时，稳定性系数与失稳概率变化关系Fig.7 Relationship between the stability factor and the failure probability when 1.05≤K≤1.1

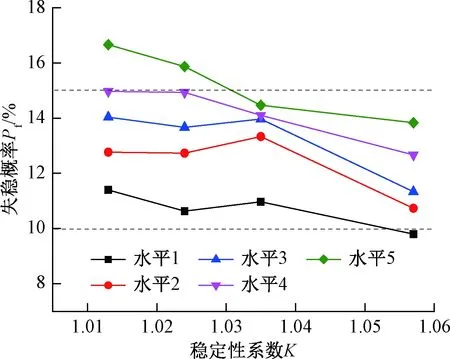
图8 1.0≤K≤1.05时，稳定性系数与失稳概率变化关系Fig.8 Relationship between the stability factor and the failure probability when 1.0≤K≤1.05

图8表明，随着变异系数的增大，边坡失稳概率增大。变异系数确定时，稳定性系数与失稳概率存在相应的对应范围。当稳定性系数介于1.1～1.2间时，失稳概率在4%～9%；当稳定性系数介于1.05～1.1时，失稳概率在6%～12%内波动；当稳定性系数介于1.0～1.05时，失稳概率9%～17%内变化。

依据相关地区地质构造图以及现场踏勘结果，“三高”地区地质条件明显呈区域状分布，以硅质岩发育为主。以典型边坡为例进行分析，总结出“三高”地区稳定性系数与失稳概率之间对应关系见表8。

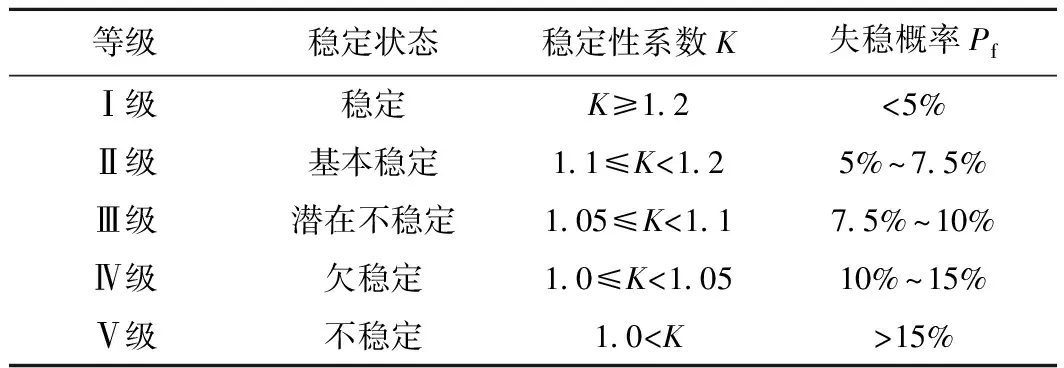
表8 “三高”地区稳定性系数与失稳概率对应关系等级划分Table 8 Classification of the corresponding relationship between the stability factor and the failure probability in the “three high” region

将G0711乌(乌鲁木齐)尉(尉犁)段高速公路岸坡稳定性分析结果进行统计(表9)。

通过对研究区岸坡稳定性分析显示，有85%以上的边坡符合表8中给定的稳定性系数与失稳概率之间对应关系。

4 结语

(1)根据现场踏勘、室内外试验资料，经计算分析发现影响边坡稳定性的首要因素内摩擦角φ具有区域分布特点，并归纳出内摩擦角φ的变异范围。

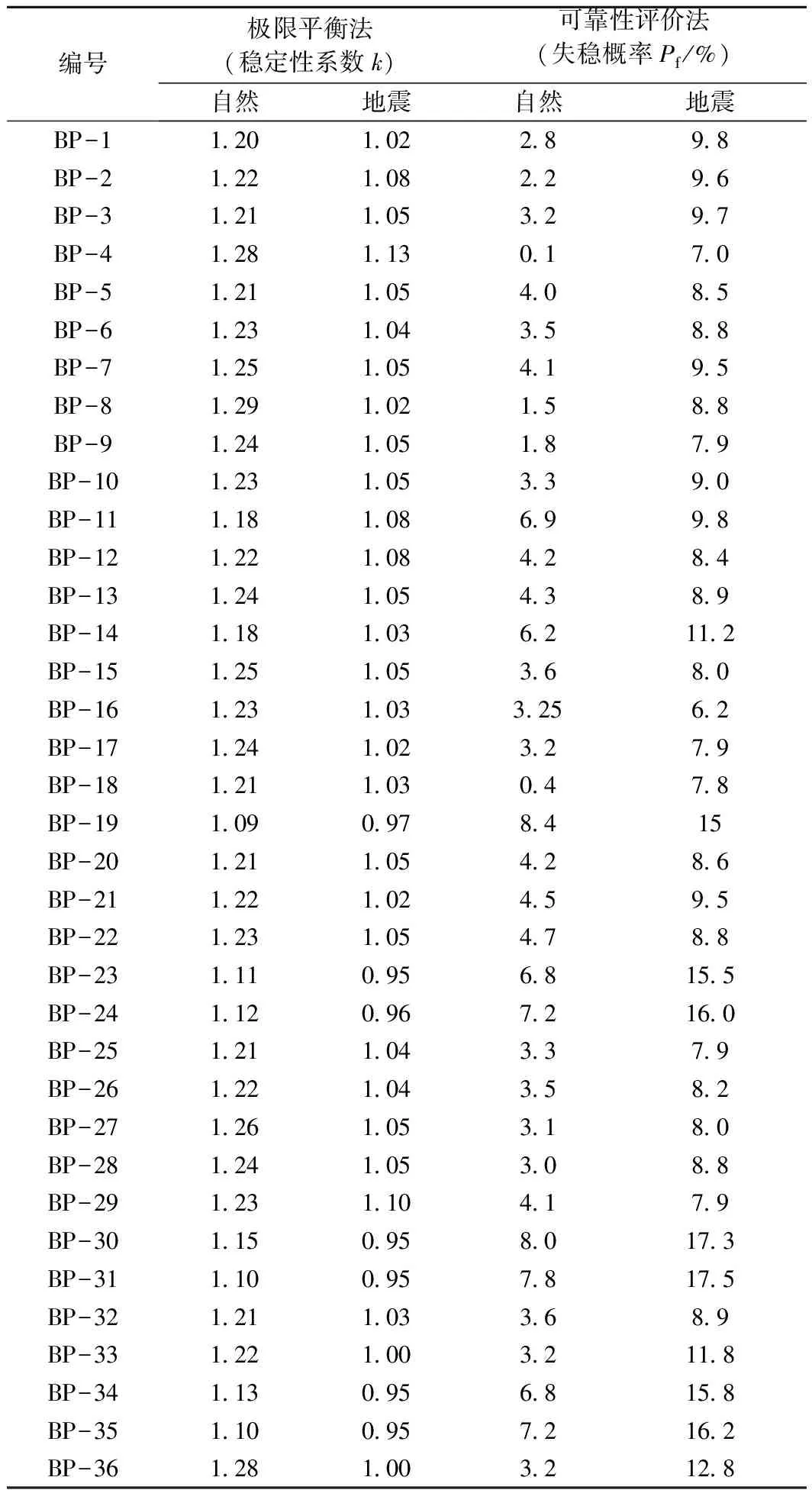
表9 G0711乌尉高速K53～K78段岸坡稳定性评价一览表Table 9 The stability evaluation list of slope at K53～K78 section in G0711 Wuyu Highway

(2)根据“三高”地区典型边坡模型可靠性分析结果显示，当稳定性系数K>1.2时，失稳概率Pf<5%；稳定性系数1.1≤K<1.2时，失稳概率5%≤Pf<7.5%；稳定性系数1.05≤K<1.1时，失稳概率7.5%≤Pf<10%；稳定性系数1.0≤K<1.05时，失稳概率10%≤Pf<15%；稳定性系数K<1.0时，失稳概率Pf>15%。利用乌尉段高速公路岸坡稳定性分析结果对其进行验证，发现所提标准具有一定的准确性，为“三高”地区边坡快速评价提供参考。