改进的静态推靠式旋转导向钻具组合力学模型

2018-10-31史玉才滕志想管志川刘庆成范致斌

中国石油大学学报(自然科学版) 2018年5期

史玉才, 滕志想, 白璟, 管志川, 刘庆成, 王恒, 范致斌

(1.中国石油大学(华东)石油工程学院,山东青岛 266580; 2.中国石油川庆钻探钻采工程技术研究院,四川广汉 618300;3.航天科工惯性技术有限公司,北京 100074)

自20世纪90年代以来,以Baker Hughes公司AutoTrak RCLS系统、Schlumberger公司PowerDrive 系统、Sperry-Sun公司Geo-Pilot系统为代表的旋转导向钻井系统(RSS)逐渐成熟并推广应用,大大提升了定向钻井技术水平[1-6]。目前,中海油研究总院、中石油川庆钻探公司均研制出了静态推靠式RSS系统,已经多次进行现场实验及应用[7-10]。为了尽快投入工业化应用,国产RSS系统还亟需提高工作寿命和可靠性、井眼轨迹调控精度和效率。笔者针对该系统的结构及工作原理,改进下部钻具组合等效处理方法,应用纵横弯曲梁理论重建该旋转导向钻具组合(RSBHA)力学模型,以期能够提高该系统的井眼轨迹调控精度和效率,为RSS系统研制及应用提供技术支持。

1 静态推靠式RSBHA的基本形式

静态推靠式RSBHA如图1所示,包括旋转导向钻井工具、柔性短节(与稳定器一体化)、无磁钻铤及MWD测量系统等。此外,有时还在无磁钻铤上接一个钻柱稳定器。

图1 典型的静态推靠式旋转导向钻具组合Fig.1 Typical static push-the-bit rotary steerable drilling assembly

以川庆钻探公司研制的静态推靠式RSS系统为例,井下导向工具的结构及工作原理如图2所示。特制的非旋转滑套上有3个可以单独控制的导向翼肋,导向钻进时3个导向翼肋伸出并支撑到井壁上,导向翼肋提供的推靠力合力称为导向力,其大小和作用方向根据井眼轨迹控制要求随时进行调整,从而在钻柱旋转条件下完成导向钻进工作[9-10]。

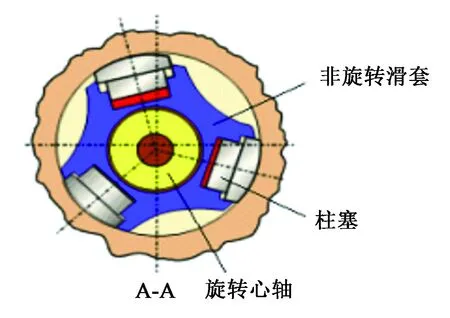
图2 静态推靠式旋转导向钻井工具Fig.2 Static push-the-bit rotary steerable drilling tool

2 改进的RSBHA力学模型

目前可以采用多种方法建立RSBHA力学模型,包括有限元方法[11-12]、加权余量方法[13]、纵横弯曲梁方法[14-16]等。其中,纵横弯曲梁方法相对简单,求解速度较快、计算精度较高,本文中也采用该方法建立RSBHA力学模型。其中,对RSBHA进行合理简化和等效处理是建模和求解的关键所在。

2.1 基本假设

采用纵横弯曲梁法建立RSBHA的力学模型时,假设[17]:钻头、钻铤、偏置机构、稳定器、柔性接头组成的BHA是小弹性变形体系;钻头中心位于井眼中心线;钻压为常量,沿井眼切线方向;由于钻柱自重的影响,上切点以上的钻柱躺在下井壁;井壁为刚性体,井径不随时间变化;稳定器与井壁之间的接触为点接触;任意一跨内没有变截面;不考虑钻柱转动和振动的影响。

2.2 导向翼肋及柔性短节等效处理方法

(1)导向翼肋的等效处理方法。现有文献[14]～[16]中将导向翼肋提供的导向力等效成一个大小和作用方向均已知的横向集中力,未考虑导向翼肋与井壁的接触作用。对于静态推靠式RSS系统,导向翼肋必须支撑到井壁上才能正常工作,忽略导向翼肋与井壁的接触作用不合适。改进方案如下:将导向翼肋等效为偏心稳定器,将该处的内弯矩和偏心距设为未知数,支座反力设为已知参数;补充两个求解条件：该支座两侧的转角相等、支座反力等于导向力。

此处以二维圆弧井眼、导向力沿井眼高边方向为例,简单推导导向翼肋对应的三弯矩方程及补充方程。如图3所示,坐标原点位于钻头中心,x轴沿井眼方向线的反方向;钻头-导向翼肋、导向翼肋-柔性短节稳定器分别为RSBHA的第1跨和第2跨梁,其上作用有横向均布载荷q1、q2,弯矩M0、M1、M2,轴向力P1、P2;第1跨梁右端(导向翼肋左侧)的转角为θR1、剪力为QR1,第2跨梁左端(导向翼肋右侧)的转角为θL2、剪力为QL2,导向翼肋的导向力为F。导向翼肋处有两个未知数内弯矩M1和偏心距Δ1。

根据上述导向翼肋等效处理方法和补充求解条件,该支座两侧的转角相等,支座反力等于导向力,表达式分别为

θR1=-θL2,

(1)

F=QR1-QL2.

(2)

由纵横弯曲连续梁的端部转角公式、剪力公式及变形叠加原理[17]可求得:

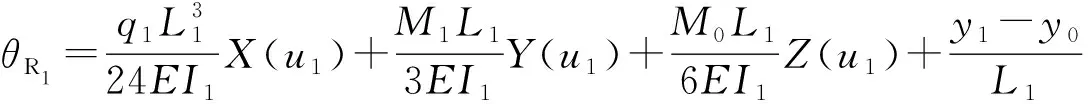
(3)

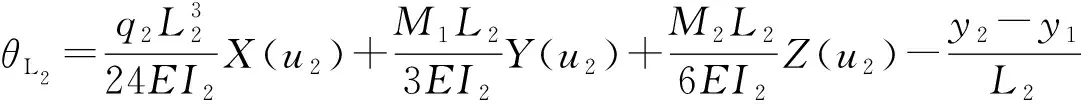
(4)

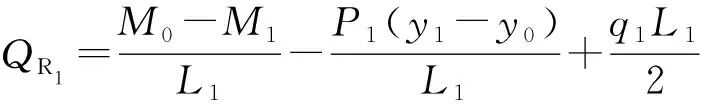
(5)

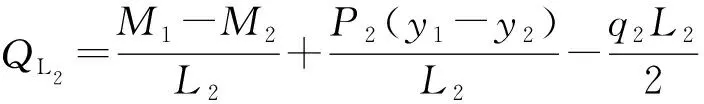
(6)

式中,E为钻柱的弹性模量;Li、Ii、Pi、qi分别为第i(i=1～2)跨梁的长度、截面惯性矩、平均轴向载荷、横向均布载荷;Mi为第i个支座的内弯矩;yi为第i个支座的高度;Z(ui)、Y(ui)、Z(ui)分别为第i跨梁端部转角的放大因子;M0、y0分别为钻头对应的弯矩、支座高度。通常不考虑钻头与地层的弯矩及井眼扩大,设定M0=0,y0=0。

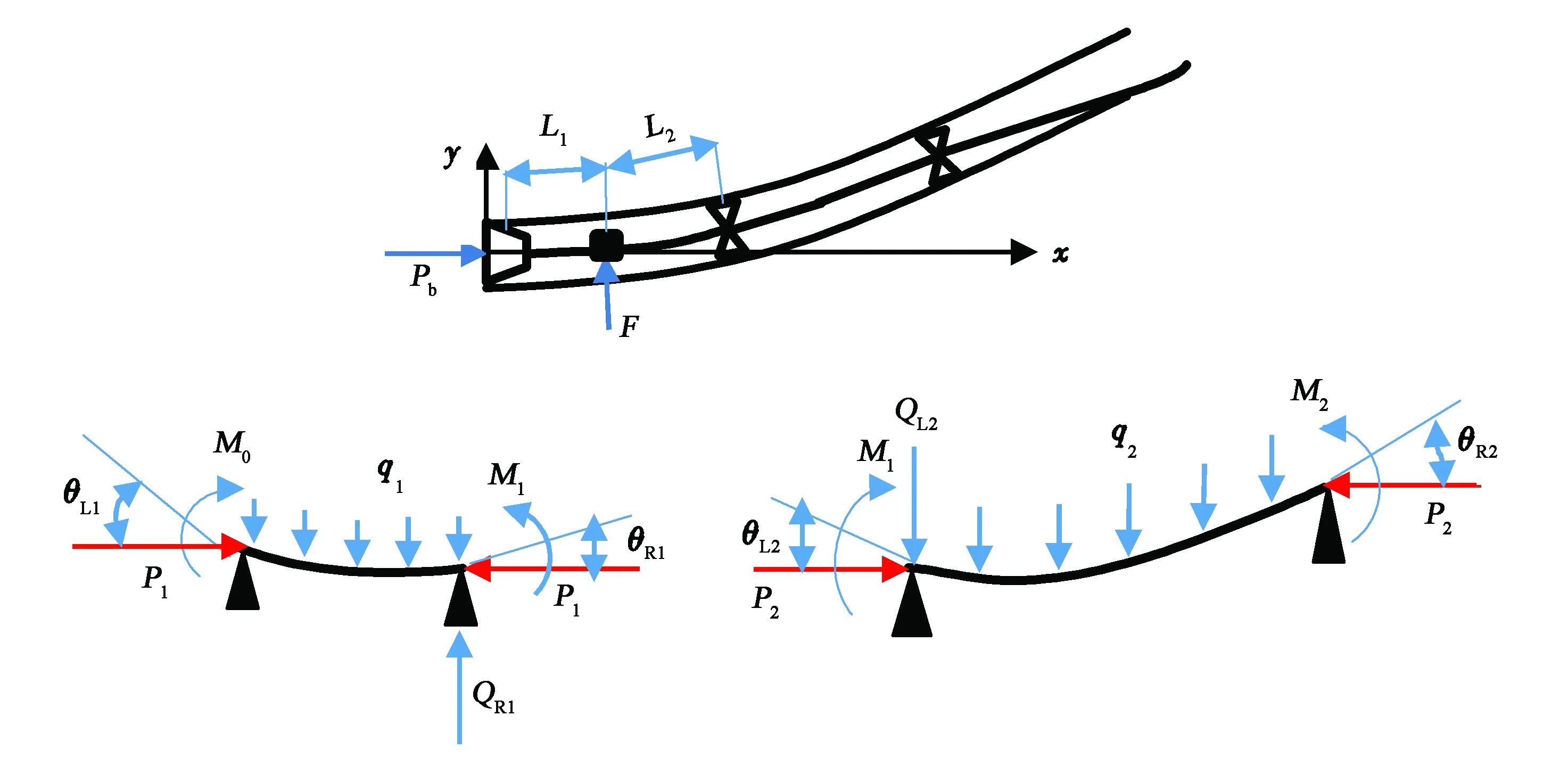
图3 导向翼肋的等效处理方法Fig.3 Equivalent method to the steering rib

将式(3)和(4)代入式(1),将式(5)和(6)代入式(2),进一步整理后即可得到导向翼肋对应的三弯矩方程和补充求解方程:

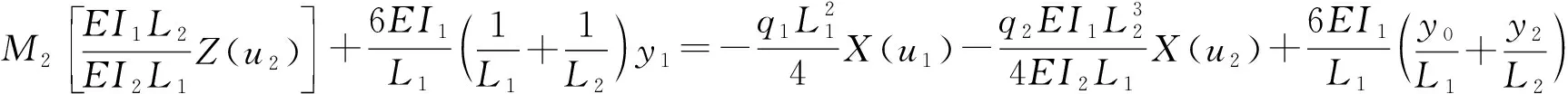
(7)

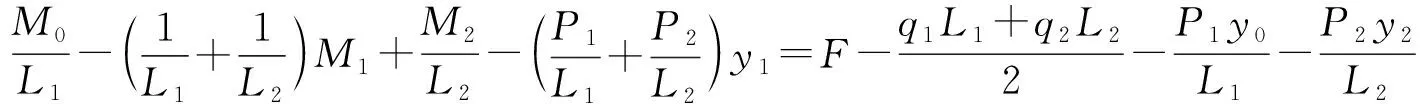
(8)

此外,某些静态推靠式RSS系统能够直接调控导向翼肋的偏心位移[18]。该情况下应将导向翼肋等效为偏心稳定器,将该处的偏心位移设为已知参数、支座反力设为未知数。

(2)柔性短节的等效处理方法。目前有两种等效处理方法:①将柔性短节的上台阶面等效为一个支座,将柔性短节所在的那一跨梁分成两跨梁[17],相应地,将该处的内弯矩和挠度设为未知数,然后利用转角相等、剪力相等条件建立两个补充方程;②利用Timshenko变刚度梁理论直接求解该跨梁的挠度和转角[19]。这两种等效处理方法均具有较高的计算精度,但是第2种处理方法的计算公式较复杂,目前多采用第1种等效处理方法,本文中也采用该方法。

2.3 BHA力学模型对应的基本方程

采用上述导向翼肋和柔性短节等效处理方法之后,应用纵横弯曲续梁理论建立RSBHA力学模型,如图4所示。将BHA从导向翼肋、稳定器及柔性短节的台阶面处截开,共分为4跨梁,依次为钻头-导向翼肋、导向翼肋-柔性短节稳定器、柔性短节稳定器-柔性短节台阶面、柔性短节台阶面-钻具与井壁的上切点。

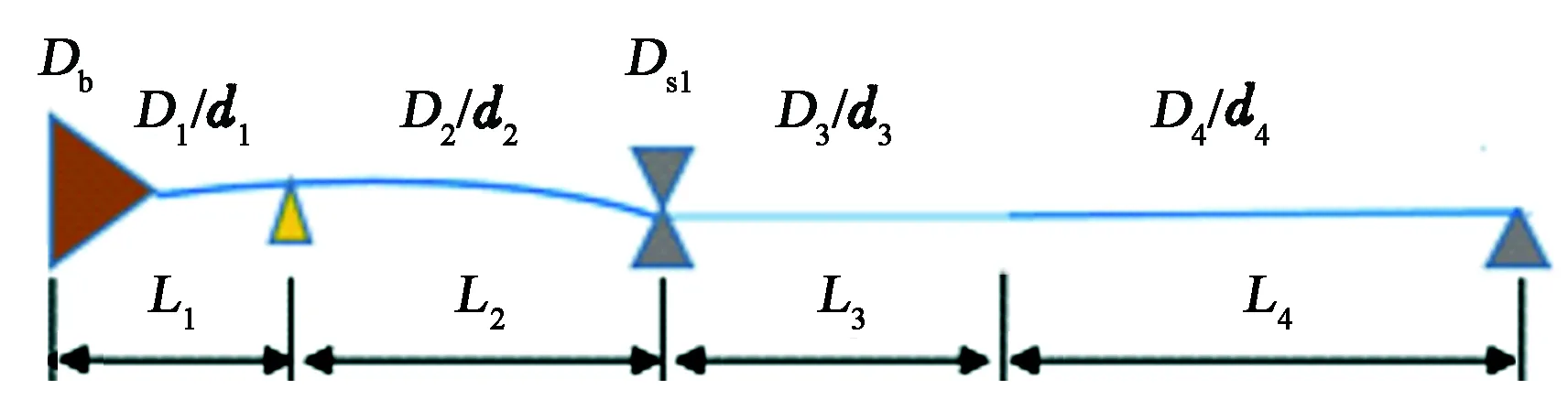
图4 纵横弯曲连续梁模型Fig.4 Continuous beam-column model

求解上述力学模型时,先推导出各跨梁端部的转角及剪力方程,然后根据各个支座处转角相等的连续条件、上切点的边界条件、导向翼肋及柔性短节的补充求解条件,分别建立各个稳定器及支座对应的三弯矩方程,以及导向翼肋和柔性短节对应的补充方程,最终可求解该钻具组合的受力与变形。

已经推导出了导向翼肋对应的三弯矩方程及补充求解方程,其余的三弯矩方程及补充方程推导方法可查阅相关文献,此处直接给出RSBHA二维力学模型对应的全部三弯矩方程及补充方程,即

(9)

式中,Li、Pi和qi分别为第i(i=1,2,3,4)跨梁的长度、平均轴向载荷和横向均布载荷;Mi为第i个支座的内弯矩;yi为第i个支座的高度;Z(ui)为第i跨梁端部转角的放大因子。

式(9)包含6个方程、6个未知数,除了M1、M2、M3及L4,y1隐含未知数Δ1(导向翼肋的偏心位移)、y3隐含未知数Δ3(柔性短节上台阶面对应的挠度)。除了上述6个未知数,其余变量的计算方法为

(10)

(11)

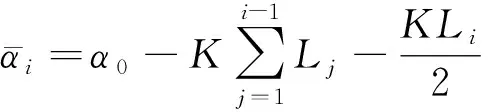
(12)

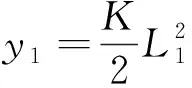
(13)

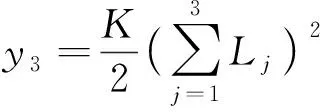
(14)

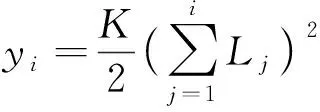
(15)

M4=EI4K.

(16)

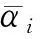
式(9)为非线性方程组,通常采用迭代法求解。实际上式(9)对未知数L4是非线性方程组,对其他几个未知数是线性方程组。利用这个特点可以对未知数L4进行试算,有助于提高求解效率。

对式(9)求解之后,可以最终求出钻头侧向力Nb、钻头转角Ab,为井眼轨迹预测做准备,

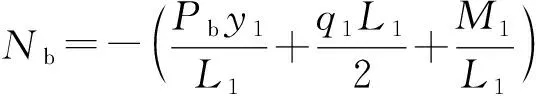
(17)

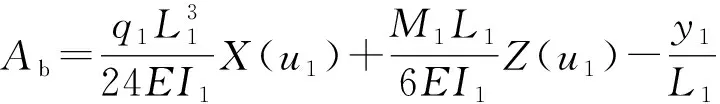
(18)

上述二维力学模型仅适用于二维圆弧井眼,且导向翼肋的工具面角等于0°(导向力沿井眼高边方向)或180°(沿井眼低边方向),除此之外均要建立三维力学模型。

三维圆弧井眼条件下,可以参考苏义脑[17]给出的BHA三维力学模型建立方法,将三维圆弧井眼和导向力分解到井斜平面P和方位平面Q上,将三维力学模型转变成两个二维力学模型进行求解。其中,给定导向力F,工具面角Ω之后,P平面上导向力分量FP=FcosΩ,Q平面上导向力分量FQ=FsinΩ。二维圆弧井眼条件下,若导向翼肋的工具面角不等于0°或180°,也需要按上述方法对导向力进行分解,将三维力学模型转变成一个二维力学模型(井斜平面P)和一个一维力学模型(方位平面Q)进行求解。利用式(9)能够直接导出井斜P平面、方位Q平面对应的基本方程组。

3 实例分析

为了检验本文中给出的导向翼肋等效处理方法及RSBHA力学模型是否更合理,并具有较高计算精度,不能直接对比钻头侧向力和钻头转角计算结果,需要结合井眼轨迹预测方法,用实钻井眼轨迹数据进行检验。

实例为长宁气田的一口页岩气水平井。川庆钻探公司研制的静态推靠式RSS系统两次下井(井深2 186～2 309、3 033～3 524 m),累积进尺超过614 m,造斜段平均钻时21.83 min/m、目的层平均钻时9.07 min/m,与邻井相同井段Baker Hughes公司AutoTrak系统的钻井指标相当。

RSBHA及相关参数:Φ215.9 mm钻头+Φ177.8 mm旋转导向工具+Φ108 mm柔性短节+Φ178 mm无磁钻铤+Φ127 mm钻杆。其中,第1跨梁的长度L1=1.05 m,外径Dc1=177.8 mm,内径d1=42 mm;第2跨梁的长度L2=2.26 m,外径Dc2=178 mm,内径d2=94 mm;第3跨梁的长度L3=1.7 m,外径Dc3=108 mm,内径d3=57 mm;第4跨梁的长度L4未知(待求),外径Dc4=178 mm,内径d4=77 mm;柔性短节稳定器的外径Ds=214 mm。钻井液相对密度1.2;钻头各向异性指数0.04;调控指令、实钻轨迹数据见表1。

采用本文中及现有文献[14]～[16]给出的RSBHA力学模型,分别计算钻头侧向力和钻头转角,然后采用文献[20]给出的平衡趋势法造斜率预测方法,分别预测造斜率、井斜角和方位角。

表1 某井实钻数据与预测数据对比Table 1 Comparison of real drilling data and predicted data in a well

注:调控指令“90 kN,100%,345°”表示钻压90 kN、导向力100%量程(22.5 kN)、工具面角345°;带“*”数据对应文献[20]给出的RSBHA力学模型。

可以看出,采用本文中给出的导向翼肋等效处理方法时,井眼轨迹参数(井斜角、方位角、造斜率)预测结果整体上优于现有导向翼肋等效处理方法。其他多组实钻数据对比分析也表明,本文中给出的导向翼肋等效处理方法优于现有等效处理方法,本文中建立的静态推靠式RSBHA力学模型能够提高井眼轨迹参数预测精度,满足钻井现场要求。