一种强非均质性油藏自动历史拟合混合求解方法
2018-10-31马小鹏王增飞
张 凯, 马小鹏, 王增飞, 刘 凡, 马 玮, 姚 军
(1.中国石油大学(华东)石油工程学院,山东青岛 266580; 2.北京中油瑞飞信息技术有限公司,北京 100007;3.中海油研究总院,北京 100010; 4.海洋石油高效开发国家重点实验室,北京 100028;5.胜利油田油气井下作业中心,山东东营 257001)
目前中国大多数油田经过长期的勘探开发,已经进入注水开发的中后期阶段,尤其是砂岩油气藏储层之间的非均质特征非常强[1-3],严重影响了油藏注水开发效果。开展强非均质性油藏中高渗通道识别技术的研究,对于油气资源开发具有重要意义。Brigham等[4-9]利用油藏动静态资料等识别复杂油气藏中的高渗通道,方法成本高,适用性局限。自动历史拟合技术依靠油藏数值模拟,根据油藏动态数据反演调整地质参数,具有很强的可靠性。目前油藏自动历史拟合方法众多[10-15],但是缺乏专门针对强非均质性油藏的方法。笔者对强非均质性油藏自动历史拟合方法展开研究,提出混合求解方法:PCA方法[16-19]与DCT方法[20-23]混合;SPSA算法[24-27]与ABC算法[28-29]混合。
1 强非均质性油藏自动历史拟合方法
1.1 历史拟合数学模型的建立
自动历史拟合问题是一个典型的反问题,通常结合先验地质信息进行求解能够得到接近准确解的结果[11]。为了得到准确的油藏地质特征,需要利用已知的观测数据与油藏模型参数m之间的关系建立数学模型,表达式为
dobs=g(m)+εr.
(1)
式中,dobs为生产动态数据;g(·)为油藏数值模拟器;εr为观测数据误差。
为了求解反问题,通常对原函数进行正则化处理,利用先验信息作为约束,对所求问题作合适的形式转换,使反问题的解更加准确。其中贝叶斯理论就是正则化方法之一,基于贝叶斯理论,观测数据与油藏模型参数之间关系式[30]为
P(m|dobs)∝P(dobs|m)P(m).
(2)
式中,m为油藏模型参数;P(m|dobs)为贝叶斯理论中的后验概率;P(dobs|m)为贝叶斯理论中的似然函数;P(m)为贝叶斯理论中的先验概率。
在地质参数m给定的条件下,获得的观测数据存在观测误差εr,一般认为误差符合均值为0,协方差矩阵为CD的高斯型概率分布,即εr~(0,CD)。因此可得到似然函数P(dobs|m)为
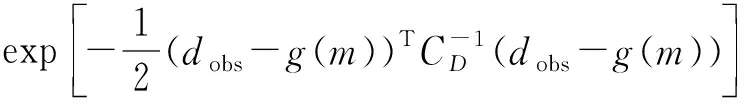
(3)
为了求得先验概率,须利用已知的油藏信息建立先验模型。本文中采用随机建模[21]方法中的序贯高斯模拟方法生成多个可选的、等概率的先验模型。目前随机建模的方法包括序贯高斯模拟、截断高斯模拟以及分形模拟等方法[31-32]。其中序贯高斯模拟主要运用高斯模型,根据离散的观测点生成一个连续的随机面,地质参数符合高斯分布规律,能够很好地反映实际地质情况,在构建地质模型领域得到了广泛的应用。因此可以得到先验概率为
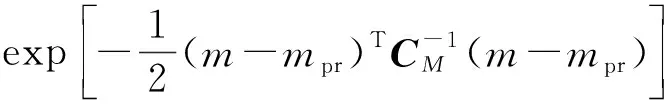
(4)
根据贝叶斯理论可以求得后验概率为
P(m|d)∝exp[-O(m)].
(5)
其中
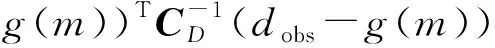
式中,O(m)为历史拟合数学模型的目标函数;mpr为先验模型参数。
后验概率P(m|dobs)中不仅包含了观测数据,还包含了先验地质信息。则历史拟合反演问题转化为使后验概率P(m|dobs)最大化问题,此过程称为MAP(Maximum A Posteriori)。后验概率越大,自动历史拟合所获得模型参数越能反映真实的地质情况。以O(m)作为目标函数,则问题就转换成求解目标函数最小值的问题。
1.2 PCA特征提取方法
主成分分析方法(principal component analysis,PCA)是目前应用很广泛的一种特征提取方法,在数据降维和特征提取方面的有效性使得它在人脸识别领域获得了广泛的应用[16-17,19]。它主要利用K-L变换从原始的数据集中提取主要特征并构成特征向量空间,而后将原有的数据影射到特征向量空间上并得到一组投影系数,能够很好地保留原始数据的主要特征信息。利用PCA方法对先验模型的非均质特征进行提取,能够很好地提取出先验模型中高(低)渗区域的信息,从而准确地反演出强非均质油藏中高(低)渗区域。
首先根据先验信息生成Ne个先验模型,记为mj(j=1,2,…,Ne),平均值为mpr。对于实际油藏的历史拟合问题,由于先验模型满足序列高斯分布,则其平均模型为
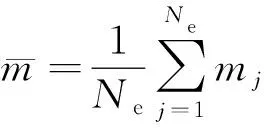
(6)
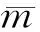
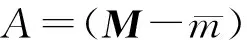

(7)
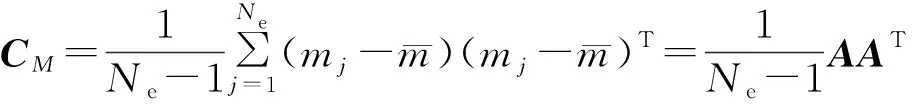
(8)
直接求CM的特征值和特征向量计算量较大,因此求解矩阵V=ATA的特征值λi及对应的正交化特征向量vi,减小计算量的同时更加准确地反映出先验模型参数场的特征,选取前p(p≤Ne≪Nm)个最大特征值及对应的特征向量;这些特征向量包含了先验模型中的主要特征信息。利用式(8)求取协方差矩阵CM的正交归一化特征向量,获得特征向量提取矩阵Φ即为原参数场的特征提取场,
Φ=[φ1,φ2,…,φe],
(9)
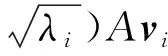
(10)
对图1表示的对数渗透率场进行特征提取,可见最大特征值λ1对应的特征提取场φ1中存在1条明显的低(高)渗通道,特征值为λ5对应的特征提取场φ5中的高(低)渗通道条数增加到3条。随着特征值的减小,对应的特征提取场中的高(低)渗通道数越来越多,因此选择对应特征值大的特征提取场进行历史拟合能够减少先验模型中无关信息的干扰,更加准确地反演出高(低)渗通道。
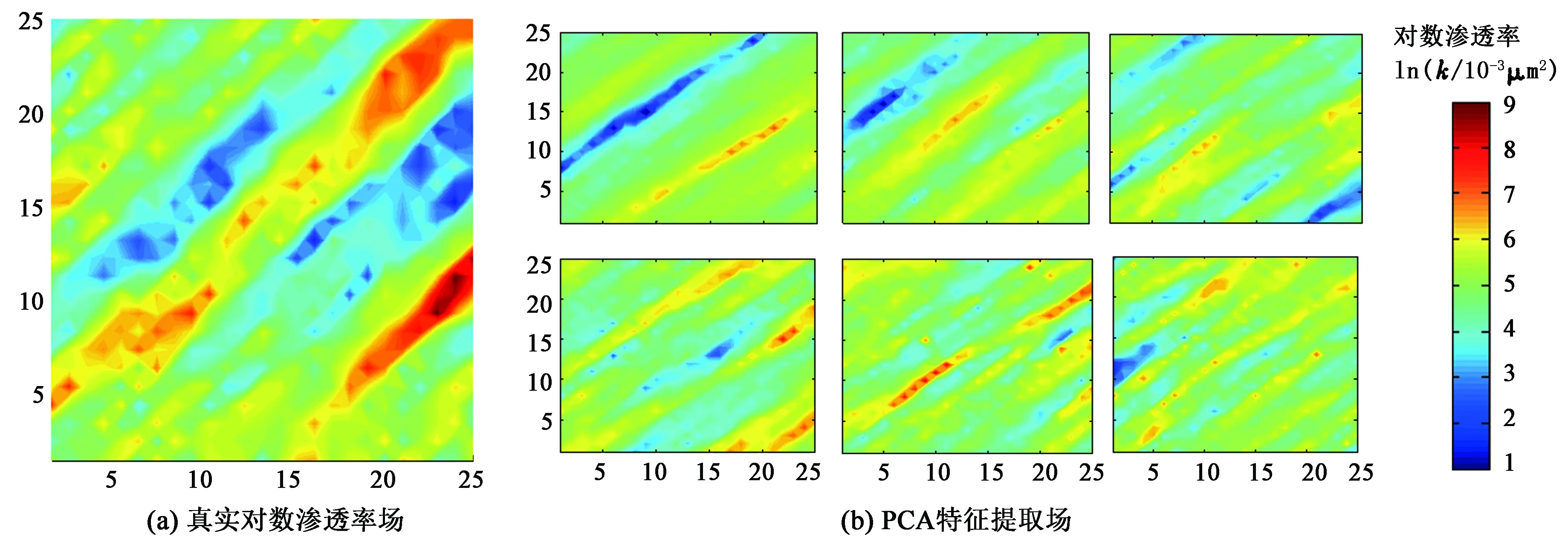
图1 PCA方法特征提取场Fig.1 PCA method to extract feature field
根据PCA方法的K-L变换原理,目标函数中协方差矩阵的逆矩阵可以被近似表示为
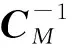
(11)
实现特征提取场Φ代替先验模型参数场M进行自动历史拟合。此时,定义新的参数s(s∈Rp)对油藏模型参数进行参数化变换,
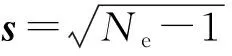
(12)
则目标函数变为
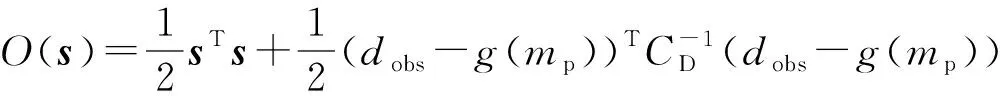
(13)
其中
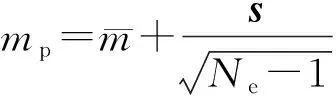
使用PCA特征提取方法可将油藏模型的历史拟合问题由Nm维降低到p维,并且有效避免了协方差矩阵求逆的过程,大规模油藏进行自动历史拟合时由于拟合参数的维数过于庞大,CM的逆矩阵计算十分耗时,避免目标函数中协方差矩阵CM的逆矩阵计算能够大幅度提高计算速度。结合优化求解方法,通过更新参数s降低目标函数值,并基于式(13)反求油藏参数,实现强非均质性油藏历史拟合问题的求解。
1.3 基于离散余弦变换的PCA降维方法
PCA方法对于高渗通道区分明显的油藏模型历史拟合,能够很好地反演出接近真实地质情况的油藏模型。但对于地质参数如孔隙度、渗透率等分布复杂的油气藏,PCA方法并不能够很好地反演出准确的储层参数,因此在PCA方法的基础上提出PCA方法与DCT方法混合进行特征提取。离散余弦变换方法(discrete cosine transform,DCT)是将一系列的离散点表示为频率不同的余弦函数的叠加。在图像处理领域,利用DCT方法良好的能量压缩性能,通过保留大系数来保存大部分的图像信息。在进行自动历史拟合时选取低频系数对先验模型进行降维,能够保留先验模型的大部分信息,从而更加精准地描述油藏地质信息。
对油藏先验模型参数场M进行离散余弦变换,D是参数场离散余弦变换后的DCT系数矩阵。定义DCT变换矩阵W1和W2,其元素分别定义为

(14)

(15)
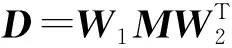
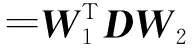
(16)
对图2表示的渗透率场进行DCT变换得到降维后的特征提取场,该变换能够更好的保留先验数据的信息,增强了历史拟合的鲁棒性。
本文中利用PCA和DCT结合进行先验模型的特征提取,PCA特征提取的参数场ΦP为(p/2)×Ne维,DCT变换特征提取场ΦD为(p/2)×Ne维。将两者组合得到特征提取场Φ代入原来的PCA方法过程即可实现PCA方法与DCT方法的混合,
Φ=[ΦP;ΦD].
(17)

图2 DCT方法特征提取Fig.2 Discrete cosine transform to extract feature
1.4 历史拟合目标函数的优化求解
随机扰动梯度近似算法[24-26](simultaneous perturbation stochastic approximation,SPSA)是通过添加扰动和重复迭代方法寻找线性或非线性目标函数的局部最优值,适用于多维变量系统,同其他随机优化方法(如遗传算法)比较,可以与任何数值模拟器耦合。在实际应用中算法的近似梯度与实际梯度方向十分接近,具有很强的收敛性。但在迭代的过程中,由于步长的选取不当,可能会导致目标函数陷入局部最优。本文中提出人工蜂群算法(ABC)与SPSA算法混合对目标函数进行求解。ABC算法[28-29]是一种较为系统的群集智能随机优化算法,具有操作简单、控制参数少、搜索精度较高和鲁棒性较强的特点,全局搜索能力较好,但局部搜索能力较差。将ABC算法的全局搜索模式引入SPSA算法中,可以提高SPSA算法的全局搜索能力。


(18)
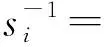

(19)

(20)
在迭代的过程中,由于步长的选取具有局限性,可能会导致目标函数陷入局部最优,此时需要引入ABC算法的搜索模式寻求全局最优值。在ABC算法中如果在一个食物源(问题的解)的位置处不能在预先设定的循环次数limit内找到更优的解,则该食物源被放弃并且被侦察蜂找到的新食物源所代替,侦察蜂搜索新的食物源依据为
sk+1=smin+rand[0,1](smax-smin).
(21)
将该搜索模式引入SPSA算法中,改进SPSA算法流程如图3所示。
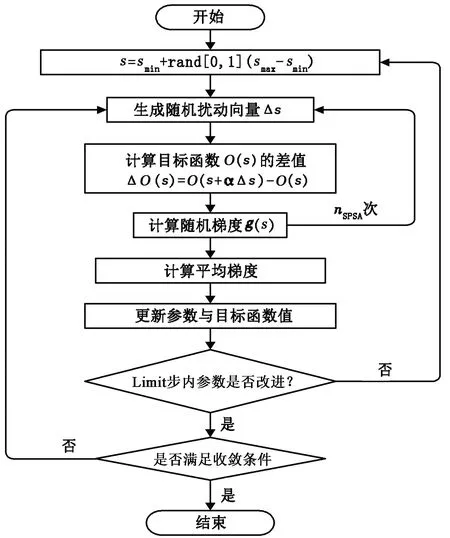
图3 SPSA与ABC算法混合优化流程Fig.3 SPSA and ABC algorithm hybrid optimization flow chart
2 实例应用
2.1 PCA方法自动历史拟合实例
对一个油气水三相的油藏模型进行PCA方法历史拟合研究,采用Eclipse软件作为油藏数值模拟器。该油藏存在三条明显的高渗通道,需要反演调整的地质参数为渗透率。用序贯高斯模拟随机生成100个先验模型,取部分如图4所示。利用PCA方法对目标函数中的先验模型参数矩阵进行特征提取,利用ABC算法与SPSA算法混合进行优化求解,渗透率场的反演结果如图5所示。可以看出,当迭代到约第5步时,注水井Inj-1、生产井Pro-2、Pro-5连线上出现了明显的高渗条带,当迭代到15步时,生产井Pro-4、Pro-3连线上同样出现了一条明显的渗透率条带。由于生产井Pro-6是单口井生产,与其他井之间不存在连通性,所以渗透率值变化很慢,直到迭代到25步时,才获得一条模糊的渗透率条带,至此反演所获得的渗透率场已经非常接近真实模型的渗透率场。结果表明,利用PCA方法提取地质参数中的非均质特征能够很好地反演出油藏中的高(低)渗通道;同时将高维地质参数数据转化为低维参数使收敛速度更快。
2.2 PCA结合DCT方法历史拟合实例
以一个油气水三相的复杂油藏模型,采用Eclipse软件作为油藏数值模拟器,进行PCA与DCT混合特征提取方法历史拟合研究,对渗透率场进行反演。采用序贯高斯模拟随机生成100个先验模型,选取部分如图6所示。然后利用PCA与DCT方法混合对先验模型进行特征提取,最后利用SPSA与ABC算法混合进行求解,结果如图7所示,可以看出求得的渗透率场在生产井Pro-1、Pro-4和注水井Inj-5、Inj-9的连线上出现了高渗条带;在生产井Pro-3和注水井Inj-4、Inj-7以及生产井Pro-2和注水井Inj-2、Inj-6连线上也出现了高渗条带。在交叉井之间,利用该方法反演出的渗透率值也十分接近真实渗透率场。对比PCA与DCT方法混合与传统的SVD方法进行历史拟合所获得的结果,可以看出相比PCA结合DCT方法,SVD方法反演的渗透率场中高渗区域并不明显,与真实渗透率场的差距较大。与单一的PCA方法进行历史拟合相比,PCA与DCT混合的方法能够获得更加精细的拟合结果,渗透率场更加接近真实地质情况。
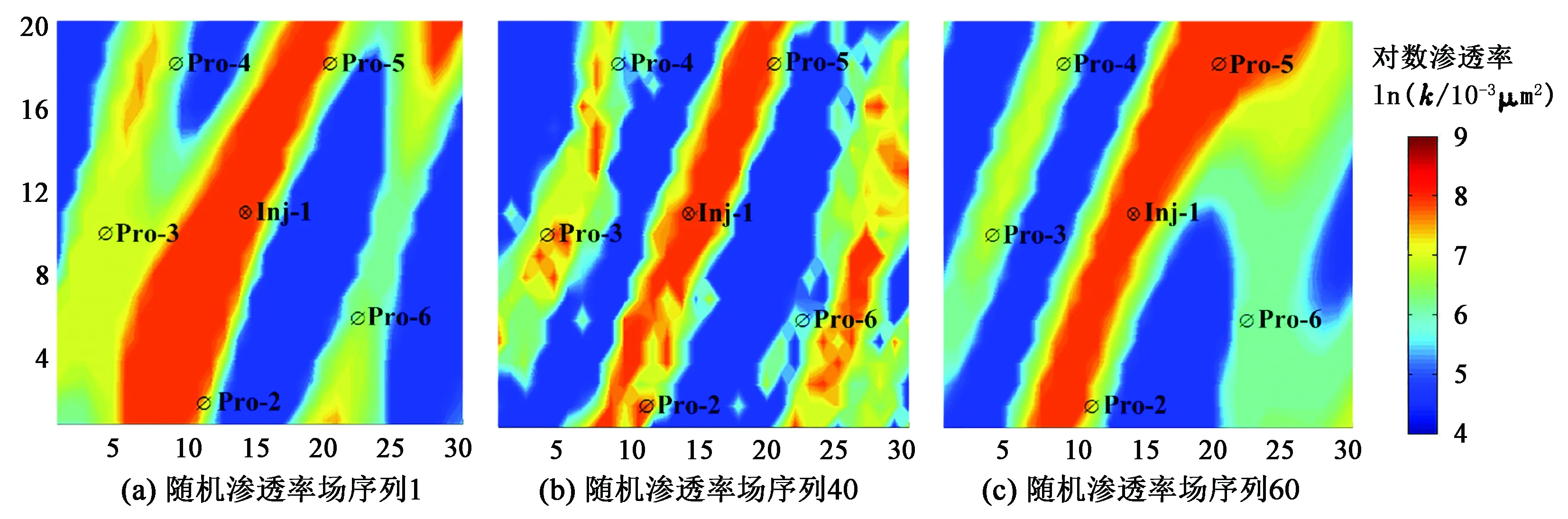
图4 初始随机渗透率场实现Fig.4 Initial random permeability field
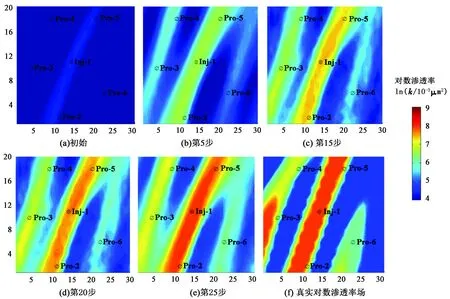
图5 渗透率场反演过程Fig.5 Permeability field inversion process
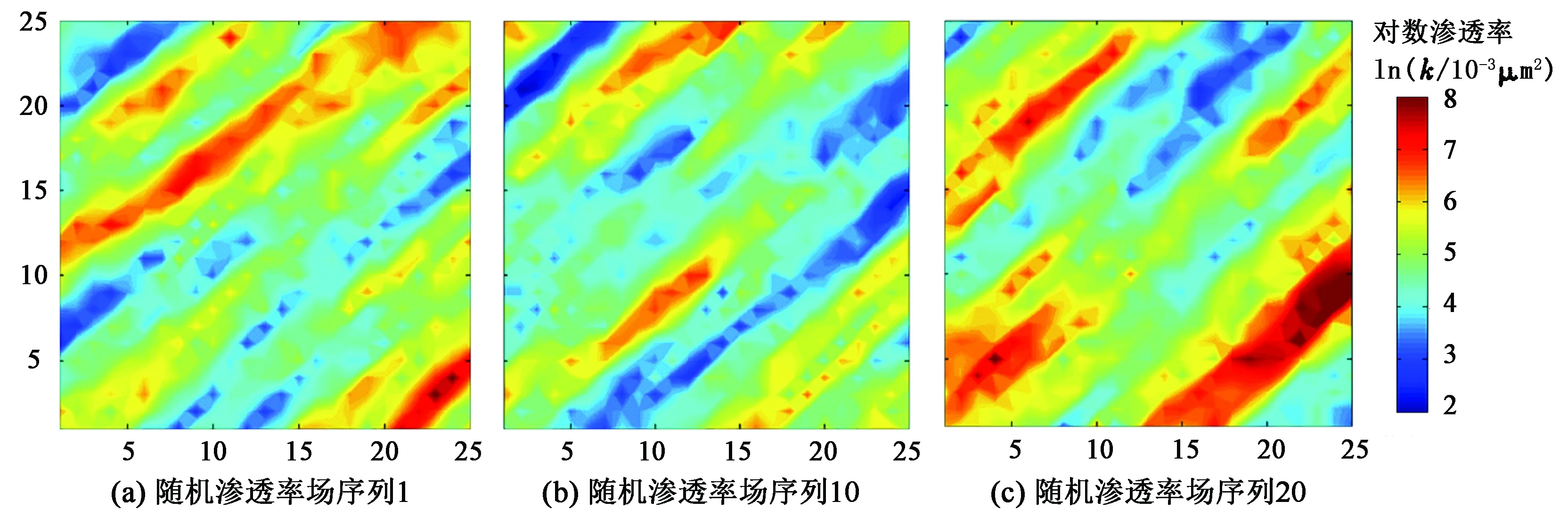
图6 随机渗透率场实现Fig.6 Random permeability field

图7 渗透率场反演结果Fig.7 Results of history matching
图8和9分别为累积指标和单井指标拟合结果。由图8可以看出,PCA与DCT方法混合拟合得到的累积产水量与地层压力随时间的变化曲线能够很好地反映真实生产数据的变化;由图9可以看出,拟合得到的生产井Pro-1的日产油量以及生产井Pro-3的日产水量随时间的变化曲线很好地反映了真实生产数据的变化。渗透率场与生产数据的拟合结果基本满足实际需要,因此提出的PCA结合DCT方法可以作为一种有效的方法进行复杂强非均质性油藏的自动历史拟合。
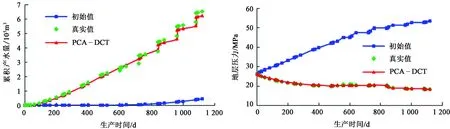
图8 累积指标的拟合结果Fig.8 History matching results of cumulative index
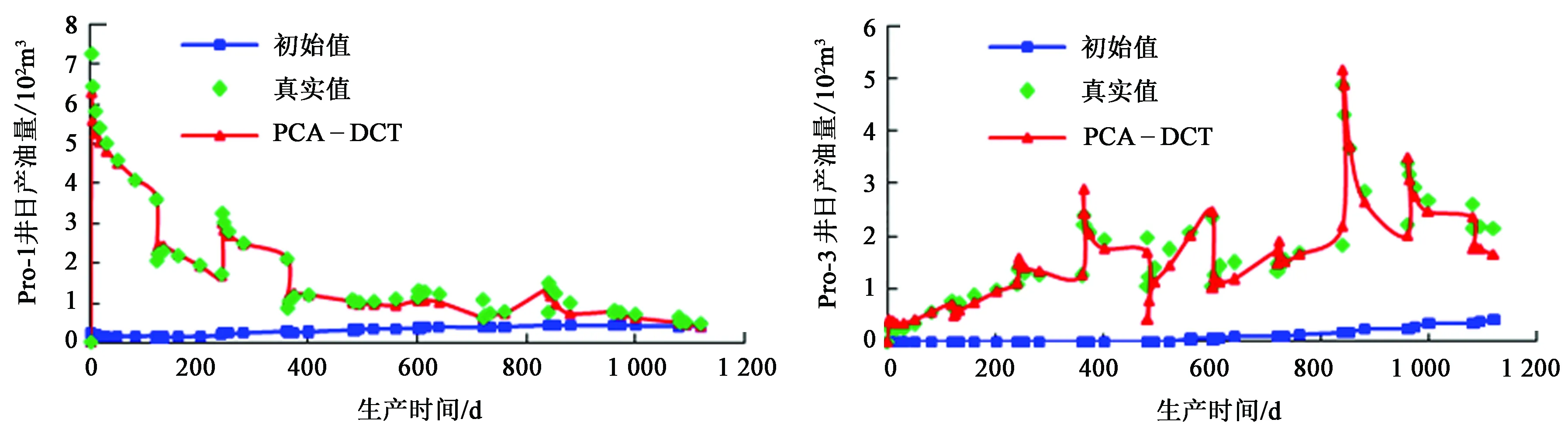
图9 单井指标的拟合结果Fig.9 History matching results of single well index
3 结 论
(1)将SPSA算法与ABC算法混合对目标函数进行求解,SPSA算法能够很好地寻找目标函数的局部最优值,近似梯度与实际梯度方向十分接近使SPSA算法具有很强的收敛性,引入ABC算法的全局搜索模式提高SPSA算法的全局搜索能力。SPSA算法与ABC算法混合提高了模型求解速度与精度。
(2)利用PCA特征提取的方法基本能够识别出油藏中的高渗通道,同时将高维地质参数数据转化为低维参数使优化算法收敛速度更快;但是由于单一的PCA方法不能提取出较为全面的储层信息,渗透率场反演结果与真实渗透率场存在较大偏差。
(3)PCA和DCT方法混合能够提取更为全面的地质特征,并且提高历史拟合的鲁棒性,很好地反演出油藏中的高渗通道区域并且反演结果更加接近真实场。提出的混合求解方法可以作为一种有效的方法进行该类油藏的自动历史拟合。
