改进BA优化的MKSVDD航空发动机工作状态识别
2018-10-30何大伟彭靖波胡金海宋志平
何大伟, 彭靖波,*, 胡金海, 宋志平
(1. 空军工程大学 航空工程学院, 西安 710038; 2. 西安交通大学, 西安 710054)
航空发动机是提供飞机飞行所需推力的装置。按照推力的大小,通常航空发动机工作状态可划分为停车、慢车、中间及中间以上、最大工作状态,在不同的工作状态下,航空发动机采用不同的调节规律提供推力,其性能参数在不同工作状态下表现出不同的函数形式和映射关系[1]。判别航空发动机工作状态,是分析发动机性能、检验发动机可靠性、在使用条件下正确利用发动机寿命等的前提和基础[2],同时,也是计算发动机控制品质的关键步骤,具有重要的研究意义和价值。
通过读取、分析飞参系统控制器记录的发动机状态参数(飞参数据),是判断航空发动机工作状态的有效途径。一般的判断方法是通过油门杆位置,但该参数难以精确区分稳态与过渡态,特别是对于军用飞机,需要在各种复杂大气条件下完成各类战斗动作,导致该参数波动较大,因此通常需要综合油门杆位置和其他参数共同进行发动机工作状态识别。在外场工作中,发动机工作状态识别由人工完成,每架次飞行记录的发动机数据量大、规律性弱,人工识别耗时耗力,因此大多存在错判、漏判等问题。
航空发动机工作状态识别从数学原理上分析属于多分类问题。支持向量数据描述(Support Vector Data Description,SVDD)[3]的本质是通过映射在高维空间的支持向量构造最小超球体使得尽可能多的目标样本包含在其中,从而达到分类的目的。该算法是基于支持向量机(SVM)发展出的一种高效的单分类方法,同样适用于多分类问题,由于该方法具有计算速度快、鲁棒性强、算法复杂度低等特点,近年来在多视点建模[4]、故障诊断[5]、模式识别[6]和异常检测[7]等领域得到了广泛应用。
在模式识别中,已有学者将SVM和SVDD应用在航空发动机工作状态识别方面,文献[8]基于最小二乘SVM比较了一对一、一对多、纠错输出编码3种分类方法,并采用纠错输出编码方法对某架次发动机工作状态进行了识别;文献[9]基于快速SVDD识别方法,构建了一种基于超椭球分类面支持向量数据描述(HE-SVDD)分类器,具有从大规模飞行数据中快速识别发动机工作状态的能力。上述文献所提方法均采用高斯核函数进行高维映射,对核参数的选取采用交叉验证的方法,但由于航空发动机飞参数据的异构性且为多数据源,采用单核函数往往达不到预期效果,而核参数的选择直接影响了SVDD的性能,同时,交叉验证方法耗时较长,且只为经验上的最优值。
为此,本文研究了多核支持向量数据描述(Multi Kernel Support Vector Data Description,MKSVDD)分类算法,结合所提出的基于混沌脉冲蝙蝠算法(Chaotic Rate Bat Algorithm,CRBA),以航空发动机工作状态识别准确率为目标函数,对多核函数权重、惩罚因子、核参数进行优化,进一步提高了分类器性能,建立了改进蝙蝠算法优化的多核支持向量数据描述(CRBA-MKSVDD)分类器,并对某型航空发动机的工作状态进行了准确识别,为发动机状态的在线或离线监控提供了应用参考。
1 多核支持向量数据描述
1.1 支持向量数据描述基本原理
设样本集合为X={xi∈Rd|i=1,2,…,n},其中n为样本数目,xi为d维的原始数据,为了提高数据的可分性和紧凑性,SVDD在构造最小超球面前使用非线性映射φ将原始低维样本特征的集合X映射至高维空间,映射后的特征向量为φ(X)={φ(xi)|i=1,2,…,n}。
根据SVDD需要将描述样本作为整体建立封闭而紧凑的目标区域可知,对最小超球体的求解实质上是一个约束凸优化问题,引入松弛因子ξi(ξi≥0,i=1,2,…,n)使得算法具有较好的鲁棒性,优化问题的数学描述如下:
(1)
式中:R为超球体的半径;C为控制最小超球体体积与非目标类数目之间的惩罚因子;a为最小超球体的球心。SVDD原理示意图如图1所示。
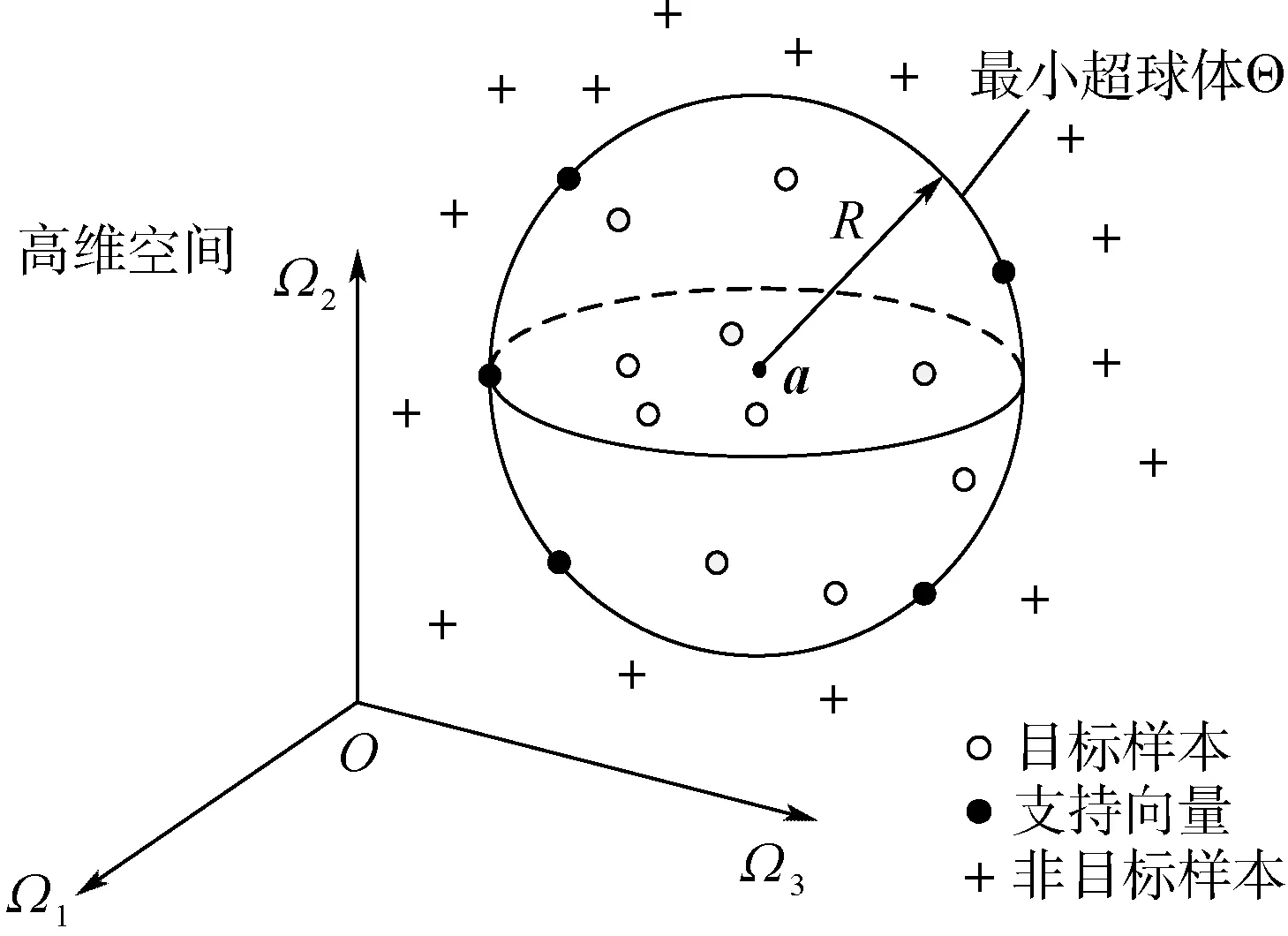
图1 SVDD原理示意图Fig.1 Schematic diagram of SVDD principle
引入拉格朗日乘子αi(αi≥0)、βi(βi≥0),在式(1)的基础上构造拉格朗日函数,可得数学形式如下:
(2)
对式(2)求极值,即对R、a和ξi的偏导数为0,分别得到如下约束条件:
(3)
C-αi-βi=0⟹0≤αi≤C
(4)
将式(3)和式(4)代入式(2),得到优化问题的对偶形式:
(5)
寻找满足Mercer定理[10]的核函数,使得K(xi,xj)=〈φ(xi),φ(xj)〉,将内积运算转化为核函数运算:
(6)
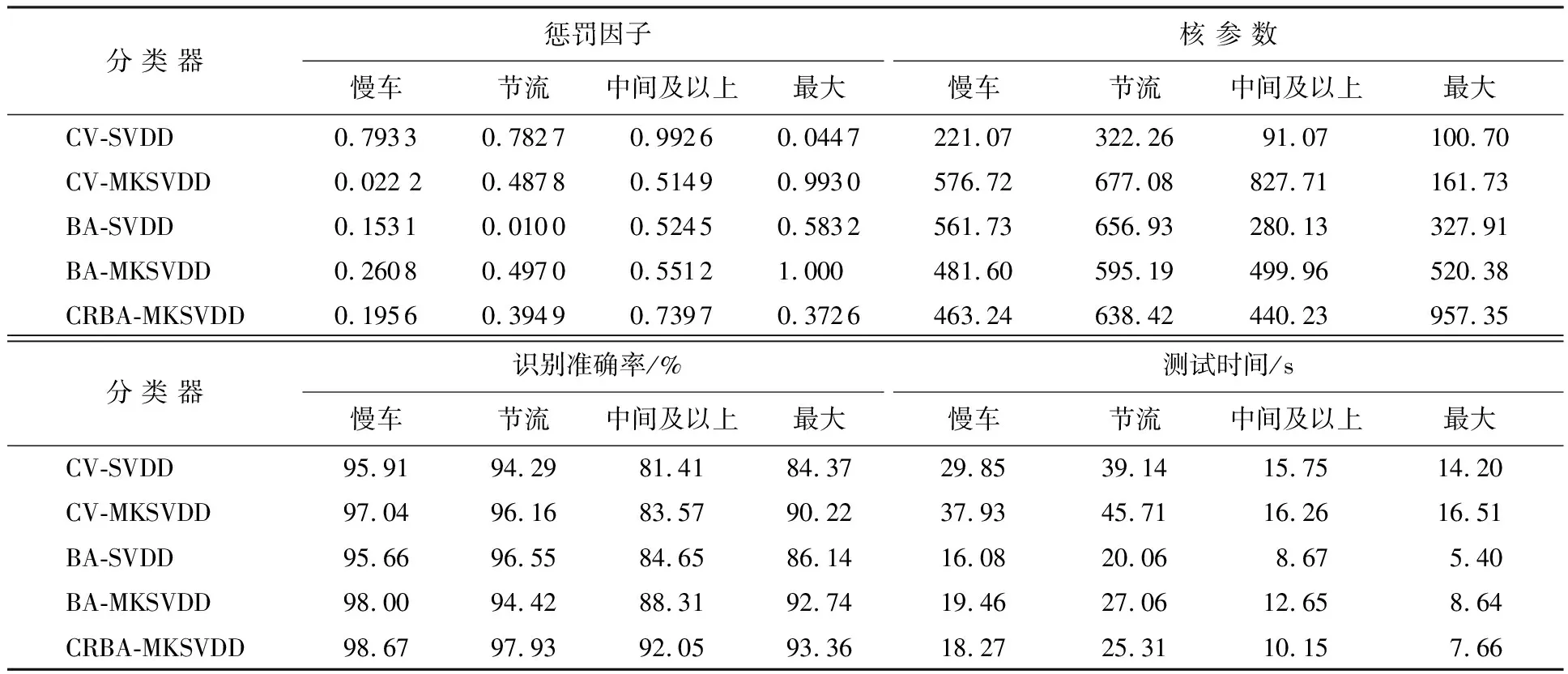
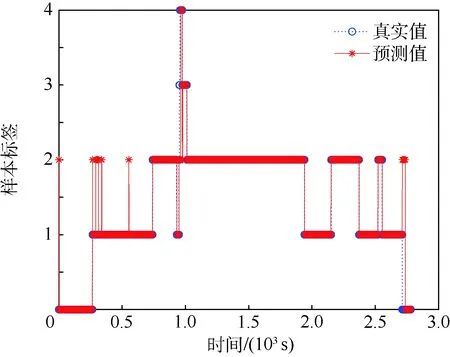
由KKT(Karush-Kuhn-Tucher)条件[11]对αi的优化结果可知,训练集中满足αi=0的点处于超球体内部;0<αi (7) 对于一个新样本,到超球体球心的距离为 (8) 判断是否属于目标样本,可根据如下列条件: Sh(x)=I(g(x)≤R2) (9) 式中:指示函数I(·),定义如下: (10) 实际数据的异构性导致单核函数往往存在局限性,不同分布类型的数据满足不同类型的核函数映射。多核函数的优点在于不同核函数的内推和外推能力不同,因而学习能力各有优劣,将不同类型的核函数组合之后兼具良好的学习能力和较好的推广能力,体现了SVDD在学习能力和推广能力之间寻求折中的思想。 因此如何构造出有效多核函数是本节研究重点。文献[12]对核函数构造的基本形式进行了研究,为了对异构数据实现更好分类效果,结合核函数使用经验,本文采用线性组合核函数的方法构造多核函数Kmulti,多核函数因子为 (11) 式(11)依次为单核多项式核函数、高斯核函数、sigmoid核函数。d为多项式核函数参数;σ为高斯核函数参数;k1和k2为sigmoid核函数参数。文献[13]已经证明对核函数进行变形,能改进核函数的性能,得到更好的分类效果,且sigmoid核函数为高斯核函数的一种形式,分类效果基本相同。文献[14]根据核映射伸缩率的性质,对传统高斯核函数进行改进: (12) 改进后的高斯核函数能够确保伸缩率rot(x)>1即在保证所有特征向量最小超球半径不变大的前提下,使得输入空间点的距离变大,具有更好的分类性能,同时通过实验表明改进后的高斯核函数比传统高斯核函数降低了VC维(Vapnik-Chervonenkis Dimension)[14]。 综上分析,由于sigmoid核函数与高斯核函数的相似性,考虑使用高斯函数与多项式核函数线性结合的形式,结合改对高斯核函数的改进策略,本文提出建立如下多核函数: (13) 式中:p(p≥0)和q(q≥0)为多核函数的权值,p+q=1。 蝙蝠算法(Bat Algorithm,BA)是由Yang[15]于2010年提出的一种新型元启发式群体智能优化算法。该算法通过模拟蝙蝠群体利用超声波遍历空间、探测目标、捕获目标、避免障碍物的生物学过程,多次迭代更新蝙蝠种群的速度、位置、最佳适应度函数值,最终得到寻优问题的全局最优解或近似全局最优解。 每一只蝙蝠在搜索空间的位置对应解空间的一个解,具有相应的速度和适应度函数值,蝙蝠群体通过更新发出频率、脉冲发射速率和声波响度产生新的解集,并逐渐进化到包含全局最优解或近似全局最优解的状态。迭代过程的数学表达式如下: Fi=Fmin+(Fmax-Fmin)RN RN∈[0,1] (14) (15) (16) 在算法收敛至最优解区域时,对最优位置进行微扰动,从而达到再次局部搜索的目的,确保最优解的遍历性,更新公式如下: Xnew=Xbest+αAl (17) 式中:α为在[-1,1]区间的随机数[16];Al为此代蝙蝠种群的声波响度平均值。 在式(17)的基础上,脉冲发射率Ri与脉冲声波响度Ai随着迭代的进行而更新,更新公式如下: (18) (19) 式中:β和ω为常数,β>0,0<ω<1。 通过对上述数学模型的分析可知,BA具有结构简单、输入参数少、可读性强等特点,实现了动态控制全局搜索和局部搜索的相互转换[17],且已被证明在求解无约束优化问题时性能要优于遗传算法(GA)和粒子群优化(PSO)算法[16],具有广泛的应用拓展空间[18-19]。虽然该算法有诸多优点,但其也存在着易陷入局部最优、收敛精度偏低和收敛速度较慢的问题。 针对这些缺点,国内外学者对其进行了研究改进,如Rahimi等[20]提出一种自适应学习的蝙蝠启发式算法,提高了BA的收敛精度;李煜等[21]融合均匀变异与高斯变异机制对蝙蝠位置进行选择性变异更新,使改进后算法的寻优精度、收敛速度均有提高;刘长平和叶春明[22]提出利用混沌优化来帮助BA实现更好的遍历性,避免局部最优值。虽然上述文献对BA进行了一定程度的改进提高,但均是对蝙蝠位置、速度更新公式的优化,没有考虑脉冲发射率与声波响度对模型及结果的影响,而脉冲发射率和声波响度是式(17)进行局部遍历寻优的触发条件和重要度量参数,蝙蝠种群回声定位的能力由脉冲发射率和声波响度控制[23],故而对脉冲发射率和声波响度进行优化和研究对提高算法整体效能具有重要意义和价值。 (20) 图2 混沌脉冲发射率变化范围Fig.2 Value range of chaotic pulse rate 为了测试本文算法的寻优性能,选取GA、PSO算法、BA和本文提出的CRBA,通过测试函数进行对比仿真,本文在此仅列举两项函数的测试结果。 Sphere函数: (21) 该函数在(0,…,0)处取得最小值0。 Rosenbrock函数: (22) 式中:I=(1,…,1),该函数在(0,…,0)处取得最小值0。 测试函数的复杂度会随着维数和迭代次数的增加而增加,适合测试算法的寻优性能。 4种算法参数设置基本保持一致,同时考虑到BA与其他智能算法之间存在最优种群参数带来的影响,迭代次数Iter依次选取为50、100、150、200,种群规模N依选取为10、20、30、40、50。为体现CRBA的优越性,BA与CRBA的脉冲发射率、声波响度保持一致R0=0.7,A0=0.9,4种算法的初始位置的最大、最小值均相同Pop_Min=-15,Pop_Max=15,初始速度根据初始位置随机生成,在此仅列出Iter=200、N=20的收敛曲线,如图3所示,其他组合种群参数的收敛结果与此趋势相同。 图3 测试函数的收敛曲线Fig.3 Convergence curves of test function 由图3可见,4类算法中GA算法具有最快的收敛速度,接近垂直下降,但其鲁棒性较差,尤其在对Sphere函数的寻优中,还有较大的振荡,BA与PSO算法的寻优效果大体保持一致,BA在收敛精度上略有提高,本文提出的CRBA算法在4类算法中兼具较快的收敛速度和最高的收敛精度,且具有鲁棒性,与其他3类算法相比较,CRBA 算法拥有最优的综合性能。 多核权重对分类效果的影响不大[13],且多项式核参数越小其外推能力越强[14],因此MKSVDD对异构数据的分类识别效果主要由高斯核参数、惩罚因子两者共同决定。根据第1节和第2节的分析,为使MKSVDD分类器达到最优的分类能力,本文设定多项式核参数d=1、多核权重p=0.6,采用CRBA,以分类器识别率为目标函数,对高斯核参数σ,惩罚因子C进行寻优计算,得到最优参数和分类器,具体步骤归纳如下: 步骤1随机初始化改进BA的蝙蝠种群参数:初始位置最大值Pop_Max、最小值Pop_Min并由此生成相应的种群位置Xi和速度Vi;设定脉冲发射率(R0=0.7)、声波响度(A0=0.9)、算法维数(DIM=2)、脉冲发射率迭代参数(τ=2.3)、频率范围;设置惩罚因子C的范围为[1/m,1],m为样本数量,改进高斯核参数为[0.1,1 000],蝙蝠个体Xi=(C,σ)与种群位置对应。 步骤2输入训练集样本,并根据算法生成的参数值(C,σ)计算第一次迭代中每只蝙蝠的目标函数值,即CRBA-MKSVDD的对训练集样本的分类准确率,并找出最优值(为符合SVDD寻优最小值准则,最优值为分类准确率的负值),记录最优值蝙蝠个体的位置Xbest。 步骤3蝙蝠种群通过式(14)计算该迭代次数内每只蝙蝠的发出频率;根据式(15)和式(16)更新速度和位置,并对速度、位置进行越界处理。 步骤4生成均匀分布随机数rand和Epsilon,若rand>R,则对当前最优解使用Epsilon进行微扰动,产生一个新的全局最优解,并对新解进行越界处理,计算新的目标函数值。 步骤5生成均匀分布随机数rand,若随机数rand 步骤6对所有蝙蝠个体的目标函数值进行排序,找出当前种群内的最优值,并记录最优值的位置。 步骤7重复步骤3~步骤6直至满足设定的最优解条件或算法达到最大迭代次数。 步骤8输出全局最优值(即分类准确率)和最优解(CRBA-MKSVDD参数值)。 本文在引言部分已指出,航空发动机工作状态识别的有效手段是读取分析飞参数据。通常需要综合油门杆位置和其他参数共同进行发动机工作状态识别,为此本节主要研究影响发动机工作状态识别的特征飞参数据选取。 特征飞参数据的选取遵循如下原则: 1) 以发动机通用规范中明确规定的技术指标及达到相应状态直接相关的主要参数为准。如在最大工作状态(简称最大状态)下要求N=Nmax;在慢车工作状态(简称慢车状态),转速Nidl通常为0.4Nmax~0.6Nmax等。 3) 特征飞参数据之间若存在耦合性,则选取相对与工况强相关的参数。如高压转速与低压转速之间存在关联,考虑高压到高压转速具有较强敏感性,选取高压转速作为特征飞参数据。 综上原则,选取高压转速(N2)、油门杆位置(PLA)、涡轮后燃气温度(T6)、燃油流量(W)、涡轮后出口压力(P6)作为判断航空发动机工况的特征飞参数据。 通过外场调研,收集到某型航空发动机某架次飞行高度在0~10 km的飞参数据,格式如表1所示。根据提供数据源方的说明,该架次飞机未进行加力飞行,对本架次航空发动机工作状态:停车、慢车、节流、中间及中间以上、最大5种工作状态设置标签(0~4),由于发动机停车状态可由转速为0直接判断,故本文仅针对慢车、节流、中间及中间以上、最大4种工作状态进行识别。 提取特征飞参数据:高压转速(N2)、油门杆位置(PLA)、涡轮后燃气温度(T6)、燃油流量(W)、涡轮后出口压力(P6),参考文献[10]的数据处理方法,作如下预处理: 1) 异常点剔除。一是由于控制品质衰退的影响,导致在飞参数据存在漂移点和明显偏离正常工作点的情况;二是飞参系统本身的记录数据本身存在系统误差。 2) 同步化处理。如表1所示,飞参数据记录时长为0.1 s/帧,各特征飞参数据由于其在飞机上的分布位置不同导致采样频率存在一定的差异,各参数在时间上不同步。对此,本文采用在0.5 s内取平均值的方法对飞参数据进行同步。 3) 归一化修正。飞参数据为异构数据,各参数的量纲不同,直接进行使用会导致数据值小的参数被忽略,因而将所有参数归一化至0~1之间。 综合该型发动机的技术资料,并按照上述预处理方法对收集到的飞参数据进行处理,最终得到24 475个样本数据,其中慢车状态数据10 129个、节流状态数据13 748个,中间及以上状态数据408个、最大状态数据190个。 由于CRBA-MKSVDD为单分类器,故而对慢车、节流、中间及中间以上、最大4个工作状态的识别需分别建立分类器。本节以预处理得到的四类样本数据为基础,各取70%作为训练集,剩余样本作为测试集,分别检验慢车、节流、中间及中间以上、最大状态分类器的分类效果。 实验过程中,依次以训练集中一类工作状态(如节流)样本为目标样本,其他3类样本(如慢车、中间及中间以上、最大)为非目标样本,对分类器进行训练,并用得到的分类器对测试集进行检验,选取SVDD和所提出的MKSVDD建立分类器,并采用交叉验证方法(CV)、BA、CRBA对2种分类器参数进行优化,体现分类器识别效果的受试者工作特征(ROC)曲线如图4(a)~(d)所示。 通过对图4的分析比较可知,在相同算法进行参数优化的条件下,与SVDD相比,所提出的MKSVDD对慢车、节流、中间及以上、最大状态的飞参数据具有更高的目标样本接受率和较低的非目标样本接受率,更适合作为分类器来进行模式识别。此外, CRBA具有更好的综合参数寻优性能,在相同优化对象的条件下,对比CV和BA,CRBA具有最快寻优速度和寻优精度;但由于MKSVDD相较于SVDD的算法复杂度较高,导致在测试时间上BA-SVDD具有最快的运算速度。 在对不同工作状态的飞参数据进行识别的过程中,CRBA-MKSVDD对4种发动机工作状态的识别率均达到90%以上,尤其在发动机中间及以上工作状态和最大工作状态的辨识中,CRBA-MKSVDD相比其他方法组合在分类效果上具有较大的提升。由于飞参数据在最大状态和中间以上工作状态下的分布范围广、振荡性、波动性强,导致所有分类器在该2种状态中的分类准确率均低于慢车、节流状态;此外,由于慢车、节流工作状态数据量较大,导致分类器在测试时间上高于对中间及以上和最大工作状态的识别。5种优化算法与分类器的组合测试结果如表2所示。 分 类 器惩罚因子核 参 数慢车节流中间及以上最大慢车节流中间及以上最大CV-SVDD0.79330.78270.99260.0447221.07322.2691.07100.70CV-MKSVDD0.022 20.48780.51490.9930576.72677.08827.71161.73BA-SVDD0.15310.01000.52450.5832561.73656.93280.13327.91BA-MKSVDD0.26080.49700.55121.000481.60595.19499.96520.38CRBA-MKSVDD0.19560.39490.73970.3726463.24638.42440.23957.35分 类 器识别准确率/%测试时间/s慢车节流中间及以上最大慢车节流中间及以上最大CV-SVDD95.9194.2981.4184.3729.8539.1415.7514.20CV-MKSVDD97.0496.1683.5790.2237.9345.7116.2616.51BA-SVDD95.6696.5584.6586.1416.0820.068.675.40BA-MKSVDD98.0094.4288.3192.7419.4627.0612.658.64CRBA-MKSVDD98.6797.9392.0593.3618.2725.3110.157.66 航空发动机工作状态识别属于多分类问题,4.3节建立的CRBA-MKSVDD属于单分类器,为此采用组合分类器的方法对发动机工况进行识别: 1) 对采集到的飞参数据进行预处理。 2) 预处理后的某时刻未知类别样本数据z,分别输入4个状态下的CRBA-MKSVDD进行决策,得到4个决策值,即{fk(z),k=1,2,3,4}(k为标签类别),采用最小决策值对应的标签类别作为t时刻样本数据的标签(发动机的工作状态kt)。判别公式为 kt=arg min[fk(z)]k∈[1,4] (23) 在上述建立好的组合多分类器的基础上,对某架次航空发动机的飞参数据进行状态识别,结果显示,本文方法对发动机工作状态的识别准确率为97.547 9%,识别效果图如图5所示。 图5 某架次航空发动机状态识别结果Fig.5 Result of one sortie aero-engine working condition recognition 该型发动机先后经历由停车状态加速至最大工作状态、在节流状态和中间及以上状态之间转换、由中间状态收油门降落至停车,整个飞行过程的工作状态识别率为97.547 9%,基本符合发动机的实际工况,体现了本文方法的有效性。 本文提出了一种基于CRBA-MKSVDD的航空发动机工作状态识别方法。 1) 提出了新的SVDD多核策略;通过引入正弦反曲映射改进脉冲发射率,提高了算法的寻优精度和速度。 2) 对飞参数据进行了预处理,并以此构建基于2种新方法的CRBA-MKSVDD分类器模型,针对发动机的不同工作状态建立了单分类器;组合不同工作状态单分类器建立多分类器,并对某架次航空发动机的飞参数据进行了状态识别。 3) 实验结果表明,CRBA-MKSVDD能够有效识别出航空发动机的工作状态,可应用于基于发动机状态的相关研究。
1.2 多核函数的构造
2 基于混沌脉冲的蝙蝠算法
2.1 蝙蝠算法基本原理
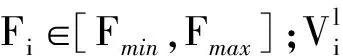
2.2 混沌脉冲发射率的优化策略
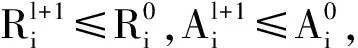
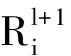

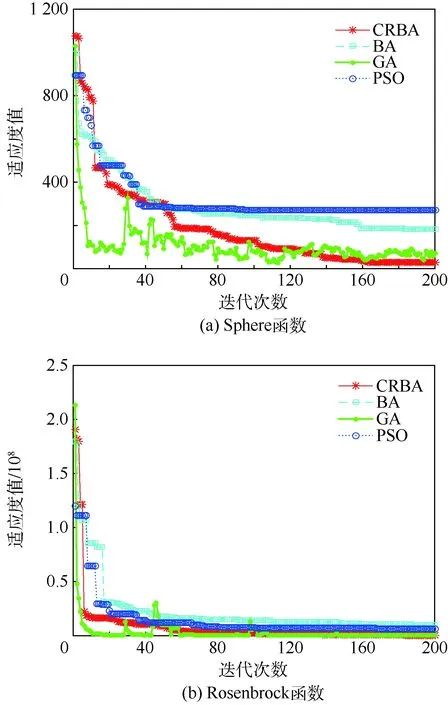
2.3 验证性分析
3 基于改进BA算法的MKSVDD参数优化机制
4 航空发动机工作状态识别
4.1 特征飞参数据选取
4.2 飞参数据预处理
4.3 基于CRBA-MKSVDD分类器的训练与测试
4.4 发动机工作状态识别实例
5 结 论
