基于磁圆二向色谱的单层MoS2激子能量和线宽温度依赖特性∗

吴元军 申超 谭青海张俊谭平恒 郑厚植‡

1)(中国科学院半导体研究所,半导体超晶格国家重点实验室,北京 100083)2)(中国科学院大学材料科学与光电技术学院,北京 101408)

(2018年4月8日收到;2018年4月24日收到修改稿)

以二硫化钼(MoS2)为代表的过渡金属硫属化物属于二维层状材料,样品可以薄至单层.单层MoS2是一种直接带隙半导体,在纳米逻辑器件、高速光电探测、纳米激光等领域具有广阔的应用前景.在实际应用中,温度是影响半导体材料能带结构和性质的主要因素之一.因此研究单层二维材料能带的温度依赖特性对理解其物理机理以及开展器件应用具有重要的意义.目前,在广泛采用的测量单层MoS2反射谱的研究中,激子峰往往叠加在一个很强的光谱背底上,难以准确分辨激子的峰位和线宽.基于自行搭建的显微磁圆二向色谱系统,研究了单层MoS2在65—300 K温度范围内的反射谱和磁圆二向色谱,结果表明磁圆二向色谱在研究单层材料激子能量和线宽方面具有明显的优势.通过分析变温的磁圆二向色谱,得到了不同温度下的A,B激子的跃迁能量和线宽.通过对激子能量和线宽的温度依赖关系进行拟合,进一步讨论了声子散射对激子线宽的影响.

1 引 言

自Novoselov等[1]于2004年首次报道单层石墨烯及其器件特性并因此被授予诺贝尔物理学奖以来,二维层状材料引起了人们的广泛关注.然而,石墨烯由于没有带隙,无法满足逻辑及光电器件方面的应用要求.而MoS2,MoSe2,WS2和WSe2等二维层状过渡金属二硫族化合物(transition metal dichalcogenides,TMDs)带隙能量在可见光和近红外波段,这使得它们在逻辑和光电器件方面具有显著的优势和广阔的应用前景.以MoS2为例,体材料MoS2为间接带隙半导体,室温的带隙约为1.2 eV.2010年,Mak等[2]以及Eda和Maier[3]分别从实验上证明当MoS2薄至单层时,会发生间接带隙到直接带隙的转变,带隙约为1.9 eV.此后,人们在单层二维材料纳米逻辑器件[4−6],宽波段、高增益光电器件[7,8],高速光电探测[9,10],纳米激光[11]等方面的研究中取得了大量的突破,展现出单层二维材料巨大的应用潜力[12−14].

大部分单层TMDs具有相似的电子能带结构,其导带底和价带顶均位于布里渊区的K和K′点[15,16].由于量子限制效应和减小的介电屏蔽,激子束缚能达到了数百meV[17,18],因此其室温和低温的光电性质均由激子主导.此外,由于强自旋轨道耦合作用,导带和价带分别劈裂成自旋向上和自旋向下的两个能带,其中导带的能带劈裂较小(单层MoS2约为5 meV),价带的能带劈裂较大(单层MoS2约为150 meV)[16],在荧光和吸收光谱上表现出两个分离的A,B激子峰(B激子比A激子能量高约150 meV).另一方面,由于单层TMDs的空间反演对称性破缺,零磁场下的导带底和价带顶在K和K′点的能量简并,自旋相反.出现了能谷相关的跃迁选择定则[19−21]:左旋圆偏光(σ−)引起K能谷的激子跃迁,右旋圆偏光(σ+)引起K′能谷的激子跃迁.这也使得单层TMDs成为非常适合进行能谷和自旋电子学基础物理及器件应用研究的材料体系.

温度是影响半导体器件性能的主要因素,研究温度变化对单层TMDs的能带结构和光学性质的影响具有重要意义.当前对单层TMDs的研究大部分都是集中在室温或者超低温(10 K以下)条件下进行的,少数变温实验也只对激子跃迁能量随温度的变化进行探讨,较少涉及谱线展宽随温度的变化.由于单层MoS2是一种典型的TMDs材料,本文基于反射型磁圆二向色谱(magnetic circular dichroism,MCD)对其激子跃迁的能量及展宽与温度变化的关系进行研究.在垂直于样品表面的外加磁场作用下,样品能带会发生塞曼劈裂,不同能谷之间的能量简并被解除.由于跃迁过程要满足能量守恒、晶格动量守恒以及总角动量守恒的选择定则,能带的塞曼劈裂导致相同波长的左旋圆偏光和右旋圆偏光吸收系数和反射系数产生差异.MCD光谱正是通过测量这种差异来对样品的能带结构和磁学性质进行研究[22−24].在单纯的反射光谱和透射光谱测试中,激子跃迁导致的谱峰往往叠加在一个较强的背底信号上.这是由于反射和透射光谱包含了衬底以及其他能量谐振子的贡献,需要通过扣除背景信号后再进行峰型拟合来提取谱线能量及线宽.我们的研究表明,背底信号的左旋和右旋偏振分量是相同的,不会体现在MCD光谱上.可以通过MCD光谱排除背景信号的干扰,直接通过确定极值点的方式来提取谱线能量及线宽.这一技术对于单层材料等本征信号较弱、背景信号较强的体系尤为有效.本文通过分析单层MoS2的变温MCD光谱,进一步研究了激子跃迁能量和线宽随温度变化的关系,结果表明MCD非常适用于单层二维材料激子温度依赖性质的研究.

2 实验原理与方法

2.1 反射型MCD的原理

在无外加磁场的情况下,单层MoS2的激子跃迁在反射谱上一般表现为高斯波包[25],可以用高斯线型对激子峰进行描述[26,27]:

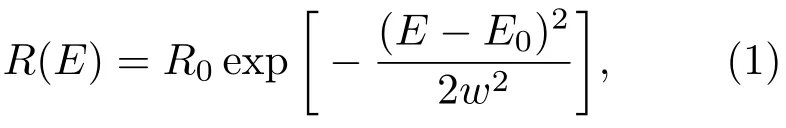
其中R0为激子峰的高度(简称峰高),E0为激子峰的跃迁能量,2w在本文中定义为线宽,其与高斯线型的半高全宽wFWHM(full width at ha lf maximum,FWHM)的关系为0.85wFWHM.对于单层MoS2,零磁场下K能谷和K′能谷的激子跃迁能量是简并的,即左旋圆偏光和右旋圆偏光的反射谱均以(1)式描述,此时两者的差分信号为零.如图1所示,左旋光反射谱、右旋光反射谱以及两者的差分信号分别用红色、蓝色、黑色虚线表示.其中,为了便于区分,将右旋光的反射谱画成了负的高斯峰,这样也可以更直观地观察两者的差分信号.在垂直样品表面的外加磁场B作用下,由于塞曼劈裂,K能谷和K′能谷的激子跃迁的中心能量分别发生红移和蓝移,移动大小为∆E/2.其中∆E为磁场下的塞曼劈裂,它与样品的有效g因子(即朗德因子)以及外加磁场强度B均成正比.由于K能谷和K′能谷分别对应左旋光和右旋光的激子跃迁,左旋和右旋的反射谱中相应的激子峰分别向低能和高能方向移动,如图1中红色、蓝色实线所示.大多数情况下,塞曼劈裂往往远小于线宽(∆E<0.1w),满足使用严格平移近似(rigid-shift approximation)[28]的条件.因此,左旋和右旋圆偏光的反射谱可以分别描述为:

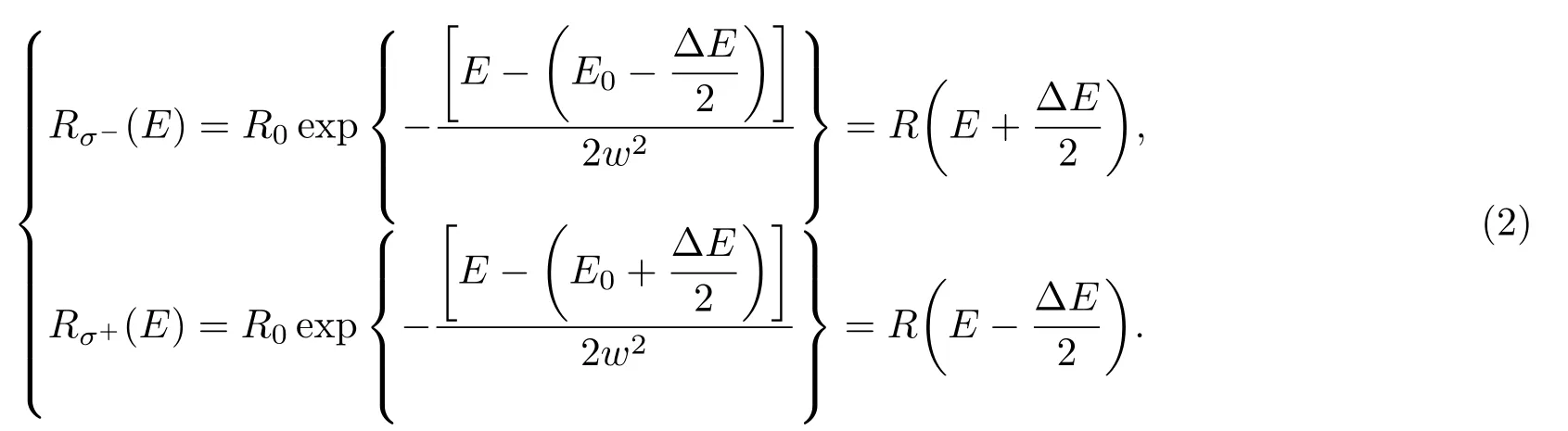
由此可以得到二者的差分反射率信号(即MCD特征信号)∆RMCD,

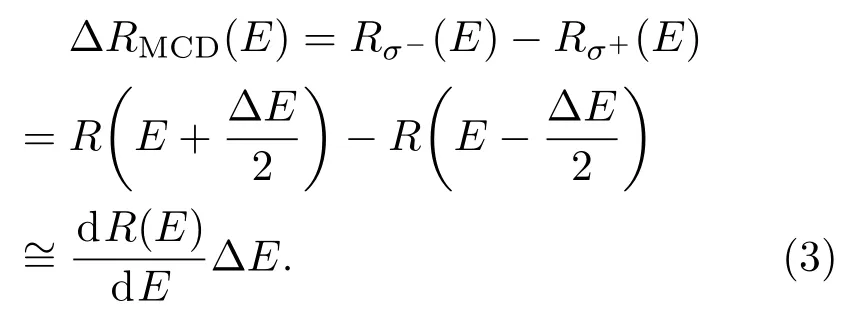
由(3)式可知,在∆E<0.1w时,MCD特征信号其实就是原始反射率谱的一阶导数与塞曼劈裂的乘积.如图1中黑色实线所示,理想的激子MCD特征信号是一个中心对称的微分线型.它以原始激子峰跃迁能量E0为对称中心,在对称中心两侧分别有一个正峰和负谷.这两者的相对位置与塞曼劈裂的符号相关.如果塞曼劈裂为正,则正峰在能量低的一端,负谷在能量高的一端;如果塞曼劈裂为

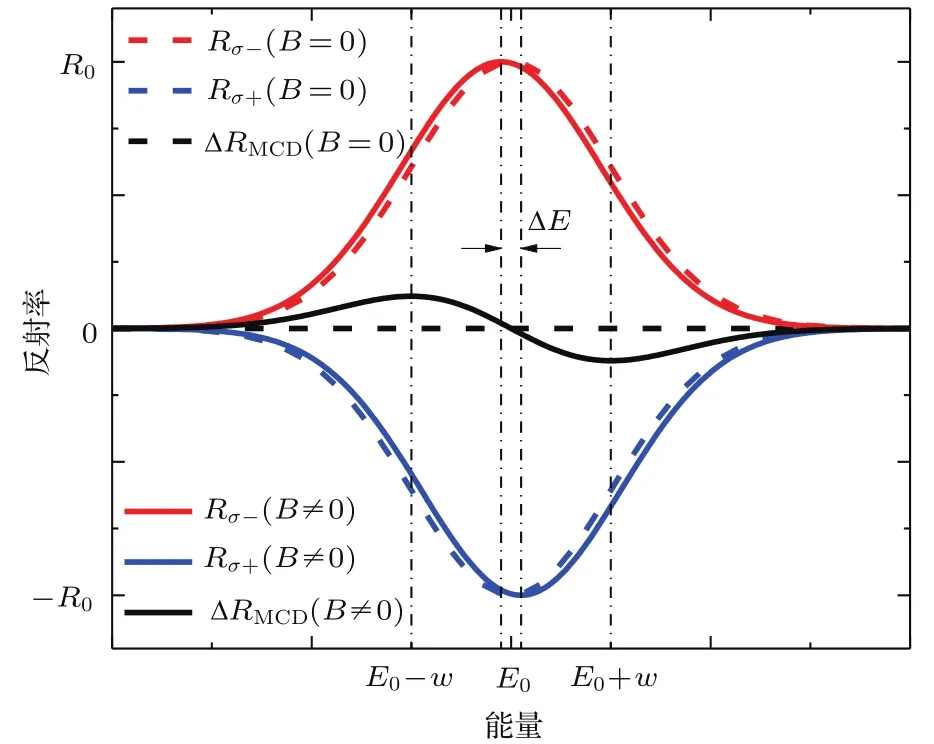
图1 反射型MCD原理示意图Fig.1.Schematic diagram of reflection MCD spectroscopy.

负,则正好相反.通过数学分析(对∆RMCD求导数确定极值位置)可以知道,MCD特征信号∆RMCD始终在EE0±w处取得极值.由此,只要找到MCD特征信号的两个极值位置,分别记为低能极值E1和高能极值E2,就可以确定原始的峰位E0和线宽2w:

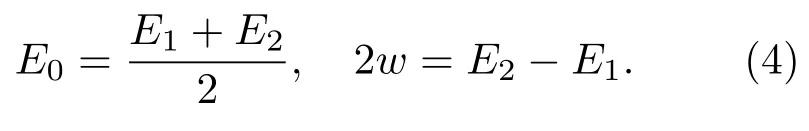
2.2 实验系统

反射型MCD的实验系统如图2所示,主要包括:1)超连续白光光源和单色仪组成的光源系统;2)格兰泰勒棱镜(作为线偏起偏器)和λ/4模式的光弹调制器(photoelastic modulator,PEM)组成的圆偏光起偏系统;3)物镜镜头、中心打孔银镜和探测器组成的反射光收集系统;4)探测器、斩波器、光弹调制器和两台锁相放大器组成的探测系统;5)超导磁体,提供不同强度的垂直样品表面的外加磁场;6)低温恒温器(图2中未画出),样品置于其中,可以调节样品温度(可变温度范围为65—300 K).

反射型MCD测量过程为:超连续白光光源经单色仪分光为单色光,单色光经过格兰泰勒棱镜起偏后变成线偏光(该线偏光的振动方向与光弹调制器的光轴成45◦角).λ/4模式的光弹调制器将线偏光周期性地变换成左旋圆偏光和右旋圆偏光,再经过物镜镜头入射到样品表面.反射光经过同一个物镜镜头收集,再经银镜反射到探测器上.探测器经过光电转换最终将光信号转换为电压信号同时送给两台锁相放大器.斩波器对入射光的强度进行调制(调制频率为177 Hz),并将相应的参考信号提供给锁相放大器1,最终得到一个反射光谱,该反射光谱实际上是左旋圆偏光和右旋圆偏光的反射光谱的平均.在严格平移近似下,可以认为就是原始的零磁场的反射光谱.光弹调制器对入射光的圆偏振度进行调制(调制频率为50 kHz),并将相应的参考信号提供给锁相放大器2.由于样品在外加磁场的作用下发生塞曼劈裂,激子跃迁导致的左旋和右旋偏振反射峰发生相对移动,最终可以得到左旋和右旋圆偏光的差分反射谱.通过改变样品的温度,就可以连续测量得到样品的变温磁圆二向色谱.

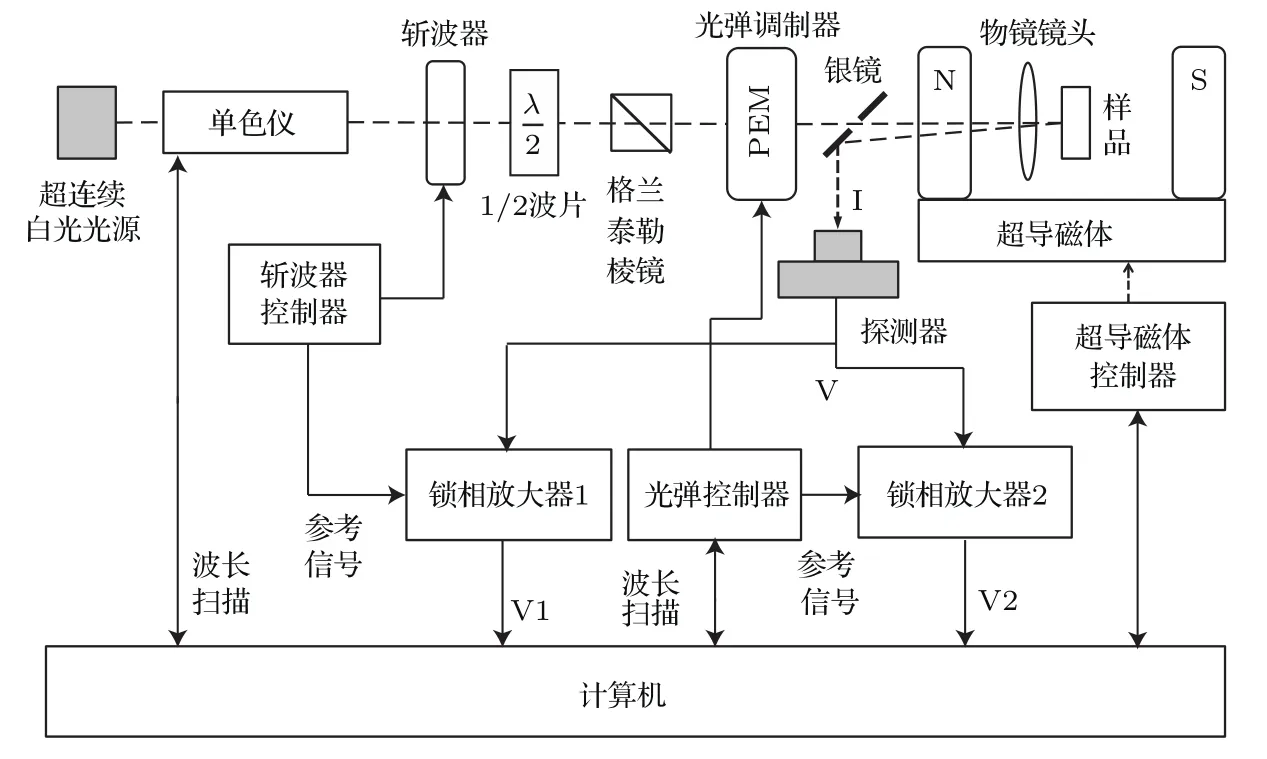
图2 反射型MCD实验系统示意图Fig.2.Schematic diagram of the experimental setup for reflection MCD spectroscopy.

在反射光谱的测量中,最理想的情况是:1)入射光谱在整个测量波段内保持强度一致;2)光路中的全部光学元件以及探测器对不同波长的响应一致[29].这样,在磁圆二色谱测量过程中得到的反射光谱和差分反射谱就可以直接看作是反射率谱和差分反射率谱.但是,实际上这两种情况都不可能满足,由此提出了两种应对方法.1)将差分反射谱与反射光谱相除得到调制反射谱,然后,再基于调制反射谱对样品能带结构进行分析.这种方法的优点在于差分反射谱和反射光谱是同时测量得到的,不仅消除了入射光谱轮廓和光路响应问题的影响,还不受入射光功率变化以及光路变化的影响.不足之处在于反射光谱实际上包含了衬底的贡献.因而使用差分反射谱直接除以反射光谱并不能完全真实地反映激子峰引起的能带劈裂.然而,由于衬底导致的反射率变化是缓变的,这样的处理对于实际的峰位和峰宽的影响一般可以忽略.2)用高反射率银镜代替样品,测量银镜的反射光谱,将其作为入射光谱,用样品的反射光谱和差分反射谱分别除以这个入射光谱即可得到样品的绝对反射率谱和差分反射率谱.这种方法需要注意的是引入了银镜反射率的影响(银镜对不同波长的反射率略有差异).同时,对光功率和光路的稳定性要求较高.由于银镜的高反射率(在测量波段反射率均在95%以上),同时超连续白光光源以及光路的稳定性很高,引入的误差可以忽略.本文采用第二种方法对测到的光谱进行处理.

针对实验系统,需要注意以下方面:1)图2中的1/2波片用来调节入射光强度.由于从单色仪出来的单色光偏振方向是固定的,格兰泰勒棱镜的角度也是固定的(因为其要和光弹调制器匹配),因此在超连续白光光源功率恒定的情况下,调节入射光的强度主要依靠1/2波片;2)物镜镜头和低温恒温器窗口的选择.在实验过程中,二者都处在强磁场环境下,因而要求二者引起的MCD信号远小于样品本身信号;3)将反射光收集到探测器上是使用中心打孔的银镜,而不是使用常见的分束镜.这是因为一方面分束镜会导致反射光信号的减小,另一方面分束镜本身往往都存在圆二色性,对测试有较大影响.在测量过程中,虽然锁相放大器对微弱的交流信号有很高的灵敏度,可以过滤掉与参考信号不同频率的噪声,但是由于测量的差分反射谱信号十分微弱(一般约为10—100µV),本实验均在暗室条件下测量.

3 实验结果与讨论

实验样品为化学气相沉积(chemical vapor deposition,CVD)法生长在单面抛光的蓝宝石衬底上的单层MoS2样品.图3(a)和图3(b)分别为单层MoS2样品在室温下的拉曼光谱和荧光光谱,使用的激发光波长为442 nm.在拉曼光谱中,可以观察到单层MoS2的两个典型模式:(约386.8 cm−1)和A1g(约404.3 cm−1),两者的频率差异为17.5 cm−1.通过洛伦兹拟合分析了样品的荧光光谱,得到单层MoS2的A,B激子峰的能量位置为别为1.823 eV和1.977 eV,两个激子峰之间的能量差异为154 meV.这些结果与以往对单层MoS2的研究一致[30−32],证明了本文样品为高质量的单层MoS2.

图3(c)为−3 T磁场下的变温反射率谱(温度范围为65—300 K).在变温反射率谱上,不仅能够指认出单层MoS2的A,B激子峰,还能直观地观察到随着温度降低A,B激子峰均发生蓝移且线宽变窄,这与常见的半导体Si和GaAs是一致的.然而,值得注意的是激子跃迁导致的反射峰叠加在一个较强的缓变背景上.这一背景来源于衬底材料以及与激子跃迁无关的物理过程.由于样品是原子级厚度薄层,因而激子跃迁的特征峰相对较弱,背景反射谱的存在干扰了激子峰位及线宽的分析.图3(d)为−3 T磁场下的变温MCD谱(也即变温差分反射谱).与相同温度的反射谱对比可以发现,每条MCD谱中均有两个与实验原理中阐述的MCD特征信号一致的微分线型,分别对应A,B激子跃迁.A,B激子MCD特征信号的正峰与负谷的位置表明在−3 T磁场下,A,B激子的塞曼劈裂∆E均为正值.∆E=gµBB,其中g为有效g因子,µB为玻尔磁子,B为外加磁场强度(−3 T),则可以判断A,B激子的有效g因子均为负值,与之前报道一致[16,20].随着温度降低,A,B激子的特征MCD峰均发生蓝移且线宽变窄,与变温反射率谱一致.更加重要的是由于背底信号与偏振无关,不会给出MCD信号.因而,通过分析MCD光谱可以更加准确地得到峰位和峰宽.

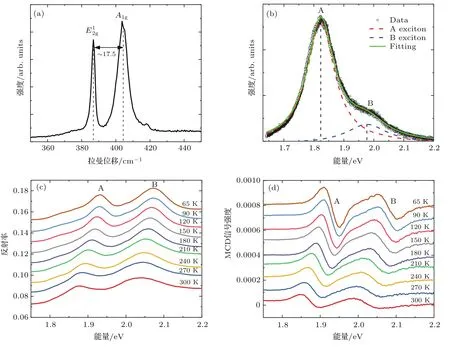
图3 单层MoS2样品在室温下的拉曼光谱和荧光光谱以及−3 T磁场下的变温反射率谱和MCD谱 (a)拉曼光谱;(b)荧光光谱;(c)反射率谱;(d)磁圆二色谱Fig.3.Room-temperature Raman spectrum,photoluminescence spectrum,and temperature-dependent reflectivity spectra,MCD spectra under−3 T magnetic field of monolayer MoS2:(a)Raman spectrum;(b)photoluminescence spectrum;(c)reflectivity spectra;(d)MCD spectra.

采用变温MCD谱,根据(4)式得到了不同温度下的A,B激子的跃迁能量,如图4(a)中的红色、蓝色散点所示.实验结果表明A,B激子的能量差异基本不受温度变化的影响,始终约为150 meV.红色、蓝色实线分别为使用Varshni公式[33]对单层MoS2中A,B激子跃迁能量温度依赖关系的拟合结果:

其中T为温度,E(0)为温度在0 K时的激子跃迁能量,α,β为Varshni常数:α表征了电子(激子)-声子相互作用的强弱,β与德拜温度相关,使用Varshni公式拟合得到的参数结果如表1所列.A,B激子跃迁能量随温度变化关系还可以使用Bose-Einstein公式[34,35]进行拟合(声子数满足Bose-Einstein分布),结果如图4(a)中黑色、绿色实线所示.

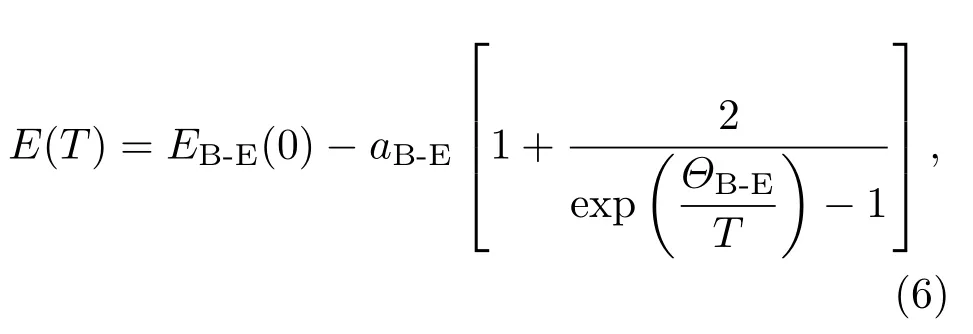
其中EB-E(0)与0 K时的激子跃迁能量相关(式中EB-E(0)−aB-E为0 K时的激子跃迁能量);aB-E反映了电子(激子)-声子相互作用强弱;ΘB-E是与全部声子(光学声子和声学声子)有关的温度量纲的常数,与德拜温度的定义类似.根据Bose-Einstein公式拟合得到的结果如表2所列.

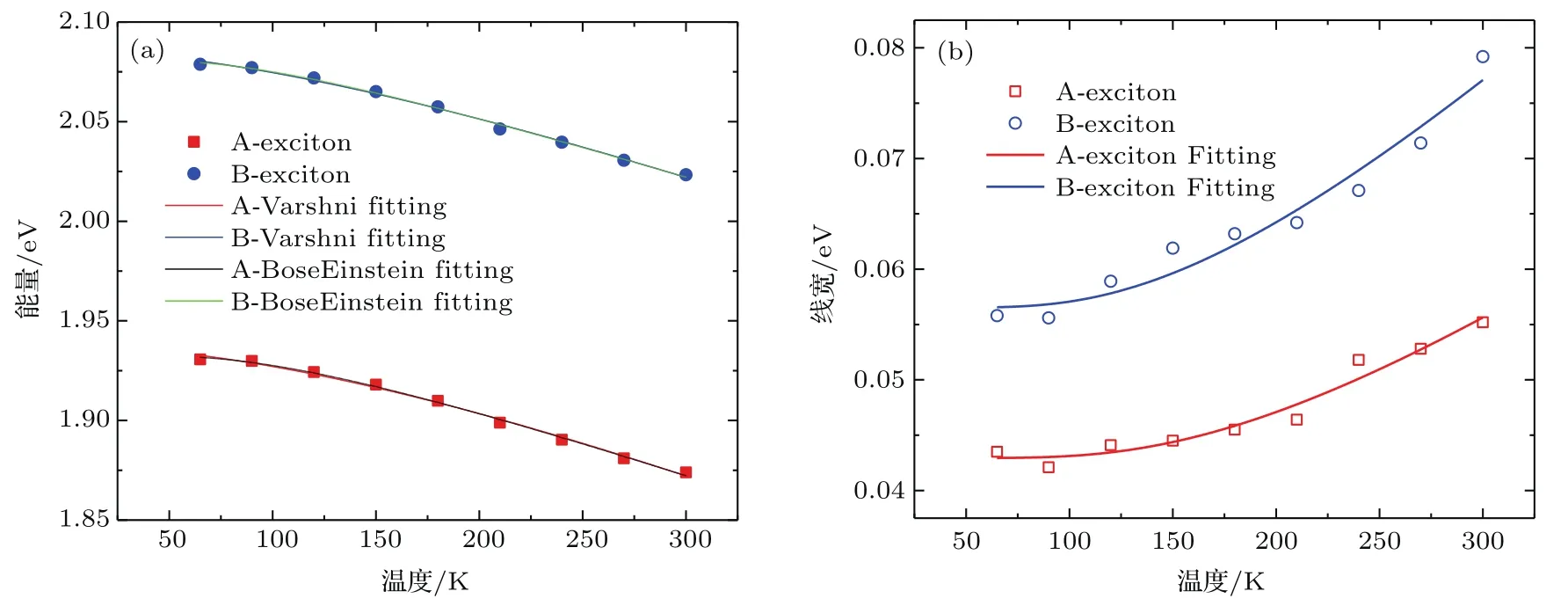
图4 单层MoS2的A,B激子的跃迁能量及线宽 (a)跃迁能量随温度的变化及其Varshni拟合和Bose-Einstein拟合;(b)线宽随温度的变化及其根据(7)式的线型拟合Fig.4.Transition energies and linewidths of the A and B excitons of monolayer MoS2:(a)Temperature variation of the transition energies fitting to Varshni equation and Bose-Einstein equation;(b)temperature variation of the linewidths fitting to equation(7).

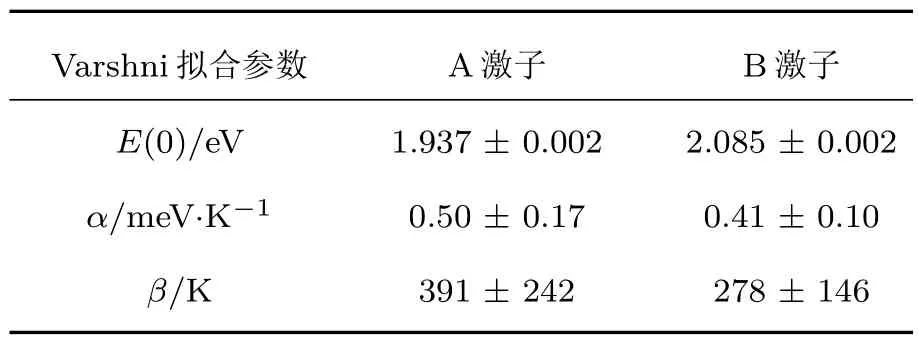
表1 单层MoS2的A,B激子跃迁能量与温度依赖关系的Varshni拟合参数数值Table1.Values of Varshni fitting parameters describing the temperature dependence of the A and B excitonic transition energies of monolayer MoS2.

表2 单层MoS2的A,B激子跃迁能量与温度依赖关系的Bose-Einstein拟合参数数值Table2.Values of Bose-Einstein fitting parameters describing the temperature dependence of the A and B excitonic transition energies of monolayer MoS2.

根据Varshni公式拟合得到的A,B激子在0 K时的跃迁能量分别为1.937 eV和2.085 eV.而采用Bose-Einstein公式拟合得到的结果分别为1.932 eV和2.081 eV.考虑到误差的存在,两种方法得到的结果可以认为是高度一致的.在高温极限近似下,可以得到Varshni公式中的α与Bose-Einstein公式中aB-E和ΘB-E的关系:α≈2aB-E/ΘB-E.根据我们的实验结果,对于A激子,α=0.50±0.17,2aB-E/ΘB-E=0.357;对于B激子,α=0.41±0.10,2aB-E/ΘB-E=0.327.在误差范围内,拟合结果符合上述关系式.

根据(4)式,还可以从MCD谱得到激子的线宽,如图4(b)所示,激子的线宽随温度变化关系可以使用下式进行拟合[35,36]:

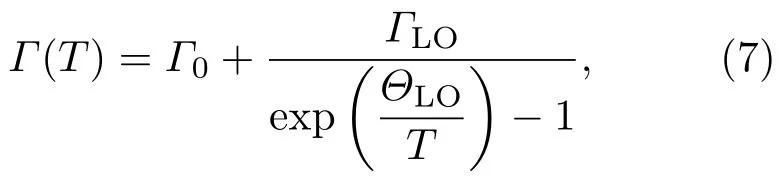
其中等号左边的Γ(T)表征线宽,等号右边的第一项Γ0代表与温度无关的物理机制导致的展宽,这些物理机制包括电子-电子相互作用、杂质、位错以及合金散射等.等号右边第二项来源于电子(激子)-纵光学(LO)声子相互作用,其中ΓLO表征LO声子与激子相互作用的强弱,ΘLO是与LO声子相关的温度量纲常数,也与德拜温度类似.根据(7)式拟合得到的结果如表3所列.需要指出的是,其他人的工作中,很多是使用(7)式对激子峰的半高半宽wHWHM(half width at half maximum,HWHM)进行拟合分析,与我们定义的线宽2w之间存在变换关系:2w≈1.7wHWHM.所以,在与他人的结果比较时,有时候需要将我们拟合得到的参数Γ0和ΓLO的数值除以常数1.7,ΘLO不受影响.

通过比较可以发现,Bose-Einstein公式拟合得到的ΘB-E远小于(7)式拟合得到的ΘLO.这是由于激子跃迁能量随温度的变化主要与晶格常数的变化以及激子与声学声子和光学声子的相互作用相关,即ΘB-E代表了声学声子和光学声子的平均作用.而线宽主要取决于LO声子与激子的相互作用.因而实验测出的ΘB-E往往远小于ΘLO,这与之前文献的结果一致[34,37].此外,根据图4(b)以及拟合的结果可以发现,相同温度下单层MoS2的B激子线宽始终明显大于A激子的线宽,这主要是由于谷间散射导致的[38].由于单层MoS2的K谷和K′谷中自旋相同的激子能态之间的耦合,导致B激子的线宽大于A激子.

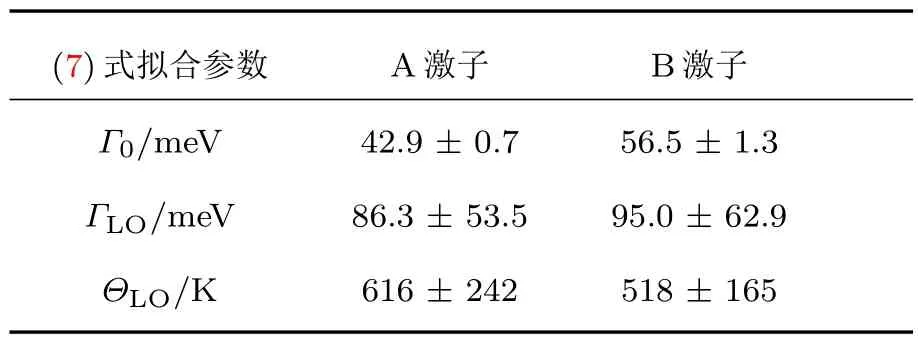
表3 单层MoS2的A,B激子线宽与温度依赖关系基于(7)式的拟合参数数值Table3. Values of the parameters which describe the temperature dependence of the A and B excitonic transition linewidths of.monolayer MoS2using equation(7).

4 结 论

采用变温MCD研究了单层MoS2的A,B激子跃迁能量和线宽的温度依赖关系.与采用反射率谱通过扣除背景信号再进行峰型拟合从而提取跃迁能量和线宽的方法相比,MCD光谱从原理上排除了与激子跃迁无关的背景信号的干扰(影响反射率,但是无MCD信号),可以更加准确地得到跃迁能量和线宽.在−3 T磁场下和65—300 K范围内,我们采用变温MCD谱进行了测量,并对激子跃迁能量和线宽与温度的依赖关系进行了详细的分析.发现单层MoS2的激子跃迁能量随温度变化和激子与声学声子及光学声子之间的相互作用相关,其线宽随温度变化主要取决于激子与光学声子的相互作用.通过进一步拟合,得到表征激子跃迁能量和线宽温度依赖关系的关键参数数值.应当指出,通过施加更大的磁场并降低样品的温度,可以进一步提升系统信噪比.研究表明,通过MCD光谱可以排除磁性无关的背景信号,非常适合于单层二维材料激子跃迁相关研究.