电子的非广延分布对复杂多组分热等离子体中(1+1)维非线性离子声孤波的影响

林麦麦，杜海粟，龚 雪

(西北师范大学 物理与电子工程学院，甘肃 兰州 730070)

近年来，复杂等离子体系统中的各种非线性波动过程的研究已经成为等离子体物理学的热门研究课题之一.Sagdeev首次在理论上研究了非线性离子声孤波的传播特性[1]；后来，Ikezi等通过双等离子体装置观测并且证实了离子声孤波的存在[2].自此以后，人们对等离子体中重要的非线性结构——非线性离子声孤波的研究产生了极大的兴趣.目前，人们从理论、实验和粒子模拟(PIC)等多方面对复杂等离子体中的一维离子声孤波问题展开了较为深入和详细的研究[3-11].早期对复杂等离子体中非线性离子声孤波的各种研究课题，大多在理论上假设电子服从麦克斯韦分布.但实际上，对于具有远距离相互作用的系统，如等离子体和引力系统，其中可能存在非静态平衡，麦克斯韦分布可能不足以描述系统.例如，实验测得的离子声波(IAW)的相速度比理论值高出70%左右，这个假设是等离子体中粒子数由麦克斯韦分布来描述的.在测量IAW的实验中，电子的能量分布实际上可能不服从麦克斯韦方程，因此很难确定有效的电子温度.因此，电子的麦克斯韦分布在处理宏观平衡系统时是有效的，却对处理有长程相互作用的复杂等离子体系统时会不太恰当[12-13].

为克服以上困难，Tsallis将经典统计热力学中的熵推广至非广延空间，并表达为[14]

其中,pi为第i个微观态出现的概率;kB为玻尔兹曼常数;q为非广延性质的参量.由于微观态的两个独立非广延系统，它们的熵具有伪叠加的性质[14]：

Silva等根据这个性质给出了非广延速度分布函数[14].目前人们已经成功利用非广延统计理论解释了诸多天体现象[15-16]，并对电子呈非广延分布的等离子体中的孤立波问题进行深入研究和讨论.

文中主要针对多组分复杂热等离子体中含有非广延电子分布的(1+1)维离子声孤波进行了理论研究.长波近似下，利用约化摄动法推导得到可用来描述无碰撞、多组分的复杂热等离子体中非线性离子声孤波传播行为的KdV方程.与此同时，通过数值模拟讨论了复杂等离子体中的基本系统参数以及电子的非广延分布对非线性离子声孤波的传播振幅、宽度以及孤立波波形的重要影响.

1 原始方程

依据磁流体力学理论，含有非广延电子速度分布的复杂多组分热等离子体中的(1+1)维非线性离子声波的原始方程组经过无量纲化过程后，简化为如下形式：

其中,

(8)

依照约化摄动方法，首先,对方程(1)-(8)中的自变量x，t作坐标伸展变换，即ξ=ε(x-v0t),τ=ε3t，其中ε是表征非线性强度的小参数，v0为线性波的速度.其次，对方程中出现的所有因变量，作如下形式的约化摄动展开:

将以上展开式代入方程(1)～(7)，按ε的不同次幂展开，在ε的最低阶近似下得到

在ε的较高阶近似下

在ε的最高阶近似下，获得用来描述(1+1)维非线性离子声波运动过程的KdV方程：

(20)

其中

2 数值模拟结果与讨论分析

为了了解非线性离子声孤波的传播特征，图1给出了等离子体的各种系统参数色散系数A随系统参数q的变化规律.从图1a可以看出，色散系数A随着q的增大而增大,这说明非广延对KdV方程的色散系数有影响.与此同时，色散系数A随着q的增大而增大，由于μ=ne0/ni0，这表明平衡态时的电子的数密度增大，正离子数密度减小使色散系数A增大.从图1b-d可以看出，色散系数A随着q的增大而增大，且随v和θn的增大而增大，但是，A随θi的增大而减小.由于v=ne0/ni0,θn=Tn/Te,θi=Ti/Te，表明平衡态时随着负离子的数密度和负离子的温度的增大以及平衡态时正离子的数密度和正离子的温度的减小而使色散系数A增大，从图1中分析还可得满足非广延的电子分布也直接影响着色散系数A.所以，等离子体处于平衡状态时的电子与正、负离子的数密度以及正、负离子与电子的温度对色散系数A均存在重要影响.

图2给出了当v,θn,θi给定不同值时，非线性系数B随着系统参数β的变化规律.从图2a可以看出，系数B随参数β的增大先减小再增大，且当β=0.6时，系数B取得最小值0，当β≠0.6时，系数B随着v的增大而减小；从图2b中可以看出，系数B随着参数β的增大先减小到最小值0再增大，且系数B在取得最小值前随参数θn的增大而减小，在取得最小值后随θn的增大而增大；在图2c中，系数B随参数v的增大先减小再增大，且当β=0.6时，系数B取得最小值0，当β≠0.6时，系数B随着υ的增大而减小；由于β=mi/mn,υ=nn0/ni0,θn=Tn/Te,θi=Ti/Te,所以，正、负离子的质量，平衡态时正、负离子和电子的数密度以及正、负离子和电子的温度对非线性系数B均有重要影响.

图1 色散系数A随参数q的变化

图2 非线性系数B随参数β的变化

为了研究孤立波的传播特性，取如下孤立波解

(22)

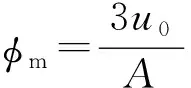
图3给出了孤波振幅φm随非广延的变化规律以及不同参数对孤立波振幅的影响.从图3a中可以看出φm随q的增大而减小，当q一定时，φm随μ的增大而减小，由此说明非广延、平衡态时正离子和电子的数密度对孤波的振幅有影响.同理，从图3b-d中可知，φm随v,φn的增大而减小，随θi的增大而增大.所以，非广延参数、平衡态时正、负离子和电子的数密度以及正、负离子和电子的温度对孤立波的振幅都有着重要的影响.综合图1和图3可知，系统参数以及非广延对系数A和振幅的影响相反，即振幅与色散系数成反比.

图3 孤波振幅随非广延参数的变化规律

图4给出了孤波宽度随不同参数的变化.由图2和图4可知，系统参数对KdV方程的非线性系数和孤波宽度的影响相同.由此可知，系统参数对孤波的振幅和宽度均有影响.还可以看出，系统参数对KdV方程的非线性系数和孤波宽度的影响相同，即非线性系数与孤波宽度成正比.

图5给出了孤立波的波形随η的变化规律；从图5a可以看出，孤立波的最大振幅随着η的增大而减小，而且在图5b-c中随着v,θn的增大而减小，

图4 孤波宽度随β的变化规律

图5 波随系统参数的变化规律

图6 孤波随非广延参数的变化规律

但是在图5d中，孤波的最大振幅随着θi的增大而增大.由此可知系统参数对孤立波的波形也有着非常重要的影响.图6表示孤立波的波形随q的变化规律.当q增大时，孤立波的最大振幅减小，这说明非广延参数的变化对孤波会产生影响.

3 结束语

文中研究了含有非广延电子分布的复杂多组分热等离子体中的(1+1)为非线性离子声孤波.通过约化摄动方法，得到可用来描述孤立波运动过程的(1+1)维KdV方程，并利用数学软件进行数值模拟研究，从理论上分析得到等离子体的不同系统参数及非广延电子速度分布对非线性离子声孤波传播振幅、宽度和孤立波波形的重要影响.研究结果表明，平衡态时的正、负离子和电子的数密度以及正、负离子和电子的温度，电子的非广延速度分布对KdV孤立波存在影响.