半日潮河口区可溶性污染物溯源

王 伟

(上海市政工程设计研究总院〈集团〉有限公司，上海 200092)

1 研究背景

某地区发生突发性水污染事件，如何在最短时间内确定污染源位置、污染物释放时间及强度等信息，并采取相应措施进行治理已是环境水力学中的主要研究课题。引起水污染事故的物质分很多种，由于可溶性污染物质在溶于水后会随水运动并发生扩散等过程，事故特征不易被发现，污染物浓度超标情况一般只能通过水质监测站测出。因此为了减小发生该类事故后产生的影响，本文针对定点排放的可溶性污染物引起的水污染事故展开溯源研究。

早前对污染源识别的研究更多的是围绕地下水开展[1-3]，而目前国内外关于对污染物在水体中的迁移转化规律以及相应的数学模型研究已经较为成熟，对突发性地表水污染事件溯源问题的研究也有了一些进展：如辛小康等[4]采用遗传算法作为优化搜索工具，运用一维非恒定水质方程解析公式构建适应度函数，分别对单点源和多点源突发水污染事故进行污染源识别；Cheng等[5]基于伴随分析法，利用后向位置概率密度函数和前向概率密度函数耦合关系，提出了一个有效的地表水点源识别方法；朱嵩等[6]针对水动力-水质耦合模型，基于贝叶斯推理，利用马尔科夫链蒙特卡罗抽样对污染源强度和质量进行估计；杨海东等[7]运用了微分蒙特卡罗方法，在Bayesian-MCMC方法的基础上，结合微分进化的繁殖思想，构造Markov链识别污染源信息；汪守东等[8]采用拉格朗日追踪法模拟油膜的输移扩散，实现了渤海海峡突发性溢油事故的模拟和预报。

近年来，由于沿海城市工业生产以及海上运输业的发展，河口滨海地区受到的水污染威胁越来越大[9]。海岸河口因其特殊的地理位置，受到潮汐作用影响，无论来自湾内或外海水体中的污染物都会影响到该河口及其附近区域的水质。虽然现在对于河口地区污染物溯源问题的研究并没有河道污染溯源成熟，但在河口地区污染物溯源时可以运用河道污染溯源的一些方法。文章结合了河道可溶性污染物溯源方法，分析河口地区潮流运动特点，以ELCIRC水动力计算模块及拉格朗日追踪法为基础，构建了基于遗传智能算法的河口地区突发性水污染溯源模型，通过构造优化模型分别回溯污染源位置及质量。

2 二维恒定流水动力基本方程及参数优化模型

2.1 二维非恒定流水动力模型

对于河口水污染问题，忽略垂直方向上的物质浓度变化及密度流影响，主要考虑河口的横向和纵向质量浓度变化，等深条件下可溶性物质的对流扩散输运方程如式(1)[10]。

(1)

其中：H—水深,m；

C—等深的物质浓度,g/L；

t—时间,s；

u，v—x、y方向上速度,m/s；

Kxx，Kxy，Kyx，Kyy—二维扩散系数张量,m2/s。

对于式(1)，一般采用有限体积法进行差分求解，Kong等[11]利用算子分裂方法，将式(1)分成对流项和扩散项两部分进行分步计算，建立水质污染模型求解出非恒定流条件下的物质浓度。

在求解河口污染物溯源问题时，未知参数的先验信息一般很难确定。文章基于近岸半日潮河口地区往复流特性，迅速判断污染物释放时间范围。利用观测浓度数据和水质污染模型计算所得数据的相关性，采用改进遗传算法构造参数优化模型，快速有效地对河口地区污染源参数进行识别。

2.2 河口地区半日潮双峰特性

在河口地区，由于受到潮汐潮流作用，近岸湾内海域以往复流为主，因此可以通过观测点位置污染物浓度随时间变化过程线大致判断出该污染源排放至观测点位置时间。图1为污染物在投放点及观测点之间运动示意图，假设污染物从A点投入，观测点为C点，B点为污染物到达的最远位置。如图1所示，由于受潮汐潮流涨落影响，污染物从投入点随落潮流运动到B点后会随涨潮流重新回到A点，时间t1为污染物从A点投入后随落潮流运动到C点的时间，t2为污染物从A点随落潮流运动到B点后又随涨潮流回到C点的时间。

图1 污染物运动示意图Fig.1 Diagrammatic Sketch of Contaminant Movement

图2为污染物排放后在观测点C观测得到的污染物浓度与时间的关系，观测时间为24 h，每隔0.5 h观测一次，从污染物开始排放时即开始观测。

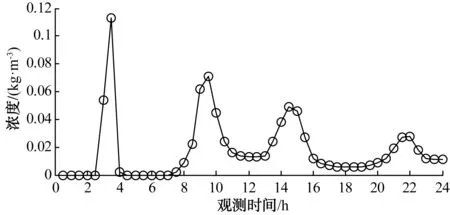
图2 观测点位置污染物浓度随时间变化过程线Fig.2 Contaminant Concentration Variation with Time at Observation Station

由图1结合正规半日潮流性质可得式(2)。

(2)

一般情况下，t1、t2的具体时间是未知的。根据所测得的数据，结合图2，假设第一个峰值时间为t1，第二个峰值时间为t2，则t2-t1是可知的，约为6 h。由式(2)可知，t1的具体数值约为3 h，其与图2中第一个峰值所在时间点一致，即从污染开始排放到第一次运动至观测点位置时的时间为3 h，这说明，可以通过观测点一系列的观测数据以及半日潮双峰特性，大致判别出污染物由源位置首次输运到观测点的时间，即污染物释放时间。

2.3 建立二维非恒定流河口溯源优化模型

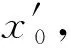
(3)

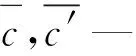
F(x,t)=min(abs(1-R))

(4)

(5)

通过式(5)构成的优化模型，可以得到污染源的排放位置x0，y0。

(6)

根据式(6)可以构建优化模型，进一步推算污染源质量。

系数ωi=1/(ci+1.0)2。

2.4 求解二维非恒定流溯源优化模型

上文将河口污染物溯源问题转化为优化问题，对于求解上述优化模型，在传统遗传算法[15]基础上，改进遗传算法使其加快收敛速度，提高计算效率。本文采用“加权法”结合遗传算法中特定步骤的改进，重新生成个体，具体计算步骤如下。

(1) 初始种群生成、变异、交叉这3个步骤均与传统遗传算法相同。

(7)

(8)

3 算例模拟结果分析

3.1 改进遗传算法验证

本节中用于验证的试验渠道信息及算例参数采集自参考文献13中的实例，该实例为2014年3月22日南水北调中线的“水质突发污染事件应急示范工程”，针对该实例已有参数及观测数据建立污染物溯源优化模型。

本文对遗传算法最大的改进在于加入了权重系数，系数的大小影响改进后遗传算法的收敛效率。理论上，α越小，收敛速度越快。由表1可知，α在[1/10，1/2)取值时，收敛效率相差不大，且适应度函数值变化不大。为了保证种群的多样性，α取值区间为[1/10，1/3]。该验证算例中选取α值为1/10。

表1 α与n、F(x)的关系表Tab.1 Relationship of α, n and F(x)

如图3所示，采用式(9)的均方差来评价收敛速度的快慢，均方差系数越大，种群散度相对较大。

(9)

其中：Fmin为x0，t0；m0为真实值时的适应度函数，此时Fmin=0。由模拟结果可知，当迭代次数小于10时，改进后算法中，适应度函数的方差总是小于传统算法适应度函数的方差，这表明，相比传统遗传算法，改进后算法能更快更稳定地收敛于真实值附近，有助于快速确定污染源的相关参数。

图3 适应度函数的方差随迭代次数变化情况Fig.3 Relationship of Variance of Fitness Function and Iteration Times

(2)改进后的微分进化算法收敛速度更快

假设7∶30时，t=0，那么9∶00排放污染物，t0的真实值为5 400 s。由图4可知：传统遗传算法在本例中迭代20次，x0、t0趋于稳定；而改进后的遗传算法只需迭代10次，x0、t0便趋于稳定，即已收敛。

图4 迭代过程曲线Fig.4 Iteration Process Curves of Different Algorithms

在实际问题中，有时并不需要精确确定污染源的相关参数，只需要确定参数范围。在这种情况下，改进后的遗传算法更凸显出优势。传统遗传算法迭代十几次才能确定的范围，改进后的遗传算法只需迭代2、3次便能做到。当给定的边界范围增大时，改进后算法能大大减小收敛时迭代次数，准确地搜索到污染源的位置、时间和质量，提高搜索效率。

3.2 二维河口非恒定流溯源算例

以泉州湾河口污染物溯源为例，泉州湾流场为近岸非恒定往复流，忽略密度流影响，该算例借鉴文献[11]中的泉州湾河口模型及计算方案，采用ELCIRC海洋模型模拟该地区流场，模拟出的流场应用于水质模型计算污染物浓度。对于泉州湾的复杂地形，ELCIRC模型采用不规则三角形网格，利用SMS生成模型所需不规则三角形网格，三角形网格数量为31 247个，节点数量为15 934个。模型开边界最大潮位位于平均海平面上4.02 m，最小潮位位于平均海平面下2.46 m。该算例水动力和水质模块是基于文献[11]中泉州湾水动力及水质模型，水动力模型计算出的观测点流速与流向与该点实测值拟合情况良好，因此文章中对于模型的可靠性及所取参数不再赘述。

该地形如图5所示，位置坐标采用平面二维坐标，污染源位置位于(9.796，18.717)，上午9点在该污染源位置处倾倒360 kg的污染物。在观测点位置(14.405，16.967)，从上午9时开始监测，每隔0.5 h观测一次，连续观测24 h，在上午11∶30开始首次观测到污染浓度数据，浓度数据如图6所示。污染源和观测位置分别在图5中以十字和空心圆标出。

图5 泉州湾地形及污染源、观测点位置示意图Fig.5 Diagrammatic Sketch of Quanzhou Bay Terrain and Locations of Source and Observation Station

图6 观测点观测数据Fig.6 Observation Data at Observation Station

3.2.1 算例系数α率定

假设已知算例中真实释放时间，对污染源位置进行优化，率定改进遗传算法系数α。权重系数α为[0.1,1]，步长为0.1，分别对不同α值进行溯源计算，比较达到相同目标函数值时所迭代计算的次数，为了减小计算结果的随机性，对每个α值重复溯源计算10次，取其迭代次数的平均值，如表2所示。

由表2可知，在α值为0.1时，其达到目标函数设定值的迭代次数相比于α取其他值时小得多，说明当α取0.1时可以更好地提高污染物位置溯源的效率，具有很广的适用性。

3.2.2 算例结果分析

由图6观测数据及湾内速度场，通过半日潮双峰特性估计的污染释放时间为165 min。考虑到观测数据峰值可能存在误差及泉州湾正规半日潮潮汐，将污染释放时间适当放大为2～3 h。根据拉格朗日追踪法，反算出大致污染源位置分别为(10.024，18.928)、(10.015，19.797)，在图7中以十字标出。根据该推算位置框定大致溯源的位置，在图7中以矩形框示出，x为(7.223，11.637)，y为(17.029，20.287)，在该范围内给定初始化种群，个数为40，选取适应度函数值较小的前20个种群，初始位置种群在图7中以浅色圆圈示出。按照传统遗传算法和改进遗传算法思路迭代，分别迭代5次和10次，得到种群位置如图8(a)～图8(d)所示。为了更清晰地表示出种群位置，图8仅截取图7中矩形框示出，图8(a)、8(b)最浅色叉形分别表示传统算法迭代5次和10次后种群位置分布，图8(c)、8(d)最浅色叉形分别表示改进算法迭代5次和10次后种群位置分布。

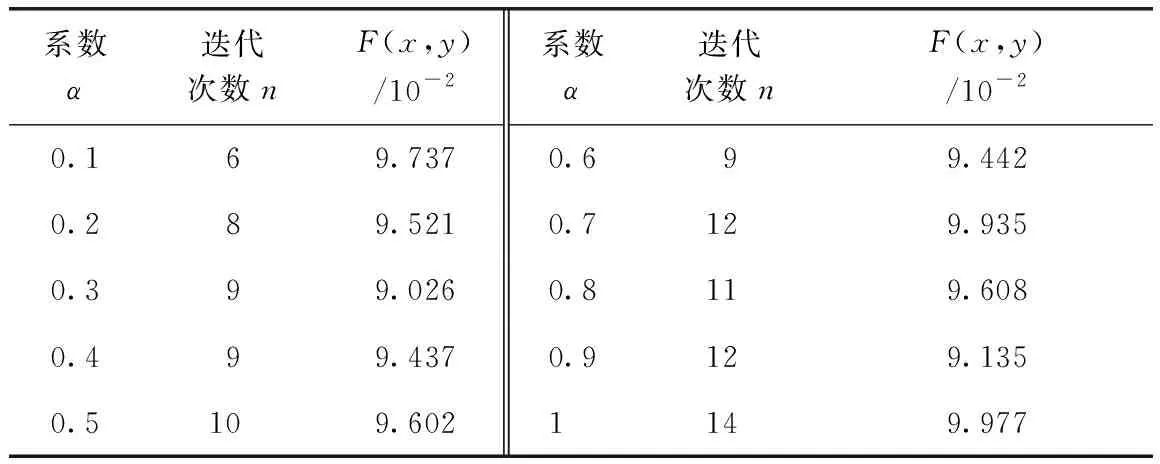
表2 不同分配系数下目标函数达到设定值(10-1以下)的迭代次数Tab.2 Iteration Steps of Different Distribution Coefficient When Objective Function Reaching Setting Value (below 10-1)

图7 溯源示意图Fig.7 Diagrammatic Sketch of Tracing to the Source

图8 传统算法与改进算法收敛速度对比Fig.8 Comparison of Convergence Rate between Traditional Algorithm and Improved Algorithm

由图8(a)～图8(d)可知，在传统和改进遗传算法分别迭代到第5次时，改进后算法中种群收敛速度明显快于传统算法，在两种算法分别迭代到第10次时，改进后算法已经收敛，并且收敛位置与源位置基本重合，而传统算法中种群虽有收敛趋势，但较改进算法速度慢得多。这说明上文提出的改进遗传算法在求解河口污染物溯源优化模型时可以更快速、更准确，极大地提高了计算效率。

得到污染源位置参数后，可以在此基础上利用优化模型进一步推算污染源质量，由于在优化质量参数时无需再计算水质模型，计算时间较短，改进遗传算法优势不明显。为了减小模型随机性的影响，重复计算20次，计算结果如图9所示。

图9 污染源质量回溯结果Fig.9 Result of Tracing to the Pollution Source Quality

由图9可知，在迭代多次后，污染源质量计算值为350～370 kg，和算例设定源强度360 kg基本一致，收敛稳定且效果很好，说明在得知污染源位置参数后，利用优化模型可以快速高效地进行污染源质量反演。本研究为了突出污染效果，将污染源质量参数放大，实际情况中污染源质量可能会略小。由于在计算污染源位置时利用相关系数法，假定的污染源质量大小不会影响到源位置的判断。

4 结论

本研究利用数据相关性，构建了河口溯源模型，结合半日潮河口地区潮流特性，采用改进遗传算法对模型未知参数进行优化，实现了河口地区可溶性污染物快速溯源，得到了以下主要结论。

(1)根据观测点的浓度观测数据，结合半日潮河口地区潮流特性，可以单独实现对污染物投放时间的快速估计。

(2)模型采用相关系数法，实现了污染源位置、质量的解耦，解放出污染源质量参数，减小了优化模型的计算量，且污染源质量大小对模型的适用性没有影响。

(3)通过改进遗传算法选择步骤，加速了算法的收敛，提高了相同迭代步数下的计算精度，这对于快速定位污染源位置及掌握污染源强度等信息并进行应急处理具有很现实的指导意义。

本研究使用的河口可溶性污染物水质模型为二维模型，没有考虑垂向浓度的变化以及密度流，适用于近海河口以往复流为主的地区，而外海多以旋转流为主，对外海海域适用性并不好。另外在发生实际污染事故时，关于污染源未知参数的先验范围可能并不全面，而在遗传算法中对先验范围估计得过大会导致寻优效率的降低，因此可以进一步探讨对未知参数先验范围的合理估计。