高层建筑外观形体比例对风载作用结构横向振动的影响∗

陈青长，刘金圣

(1.上海应用技术大学城市建筑与安全工程学院，上海201418；2.中国建筑上海设计研究院有限公司，上海200235)

0 引言

众所周知，高层建筑的结构外观与风荷载的力学特性有着紧密的内在关联，风载作为空气在流动过程对建筑结构物所作用的压力，是主要侧向荷载之一，往往直接引起高层建筑等高宽比较大结构的横向振动，威胁到建筑物的安全和舒适性能[1].近年来，随着高层乃至超高层建筑项目在全球各地的大幅度开展，风荷载变得越来越重要.地球气候日益恶化和风灾频现，也使得风载成为部分地区建筑设计中所要考虑的主要荷载之一[2].如何降低风荷载引起的横向振动响应是建筑设计选型所要考虑的重要问题.

世界各国都很重视结构抗风的研究[3,4].为了指导结构抗风设计，各国都制定了关于风荷载的专门规范，例如，在中国，荷载规范[5,6]是建筑结构设计关于风荷载的最基本依据之一，给出了规则截面建筑结构物在各个面的体型系数，主要采用等效静力法将静态设计风载乘以“风振系数”来考虑动态问题，然而这样的计算结果精度并不高.此外，关于建筑物顺风向振动的研究非常多，方法主要包括数值仿真[7,8]和风洞实验研究[9,10].关于矩形截面的高层建筑结构物的风载，梁枢果等[9]先后研究了四种不同长宽比的高层建筑的升力系数和横风谱特征;Gu和Quan[11]基于大量风洞试验研究，指出以风速相干函数代替风压相干函数计算高层结构物的顺风向响应可能会导致计算结果误差过大.关于矩形截面高层建筑的整体风载，沈国辉等[12]开展了B类地貌七种不同长宽比建筑的测压风洞试验，研究发现长边垂直方向的体型系数最大值会位于正迎风角度，而短边垂直方向的体型系数则会随着建筑结构物的长宽比的增大而递减.已有研究结果均表明高层建筑体型对于高层建筑的风载响应比较敏感.外观体型，尤其是迎风面和侧风面的体型系数，对高层建筑的顺风向振动响应的影响，作为固体力学、流体力学和优化理论等多学科的交叉领域问题，能够为指导工程实际提供重要的理论依据[13].然而，这方面的机理研究目前尚未见报道.为此，文章以目前国内最常见的标准矩形截面高层建筑为例，通过建立结构振动方程，求解不同外观形体比例下结构物的风致振动响应，从而掌握结构物顺风向效应的规律.

1 力学建模

由于高层结构物的风致振动对建筑体型敏感，该节讨论风效应比较小的平面图形，即一类矩形等截面均质高层结构物，设其高度为H，迎风面宽度为D，侧风面宽度为B，材料的抗弯刚度为EI(常量)，材料密度为ρ(常量)，截面面积A=BD，受风载荷作用为q(t).该结构承重可抽象为一端固定一端自由的竖向Euler悬臂梁，横向作用动载q(t)，如图1所示.矩形截面高层建筑的体型系数(Body Shape Coefficients of Rectangular High-rise Building)为

图1 矩形截面高层建筑计算简图

分别表征迎风面和侧风面的体型系数.考虑该结构为粘弹性悬臂梁，可设梁的本构关系为

其中E为弹性系数，η为粘性系数.考虑梁的小变形，即

则梁横截面的弯矩为

其中

因此，用横向位移表示的梁单元力学方程为

其中q(t)为风载荷集度.

2 振动响应求解

本节主要求解平均载荷和脉动载荷下力学模型的振动响应.由于梁单元横向位移的力学方程(6)满足边界条件

可取满足这一边界条件的位移模式

对于一般的竖向悬臂结构，仅需考虑结构的第一阶振型所带来的影响，因此将上式代入（6）,应用Galerkin原理，有

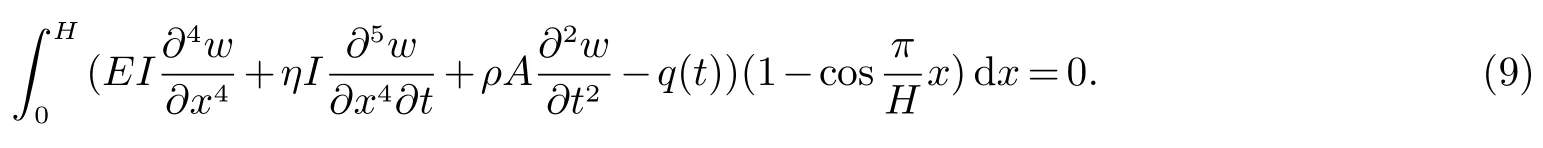
分项积分得

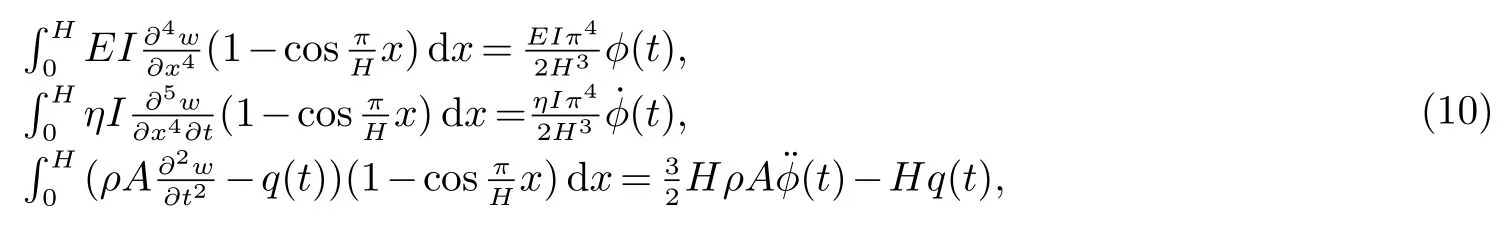
将（5）式代入（9）式，整理得

其中

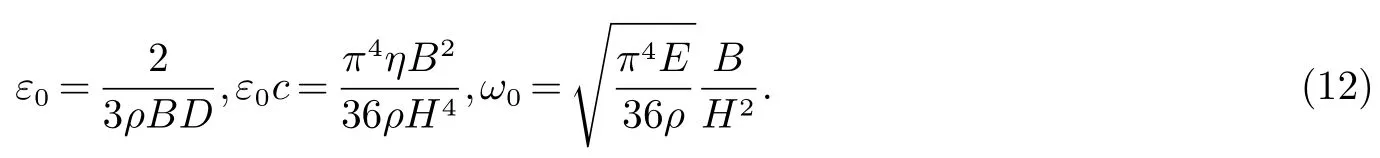
与地震冲击相比，风荷载的持续时间比较长，往往达到几十分钟乃至几小时.作用于建筑结构物上的风载可分为平均风和脉动风，首先考虑风载为常载，既平均风，表示为q(t)=Q，则可设φ(t)=(t)+ψ0，代入（11）式求解得

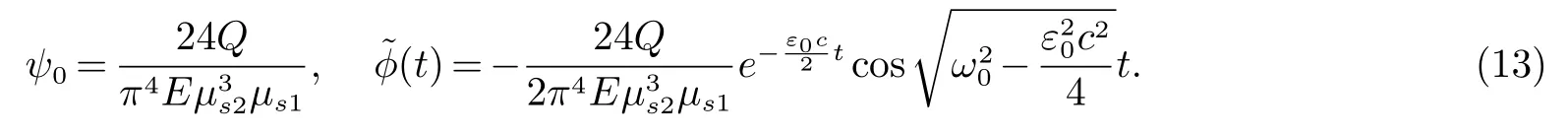
因此梁单元的振动响应为

上式说明悬臂梁的挠度随时间衰减，结构物沿纵向梁单元的最大挠度为

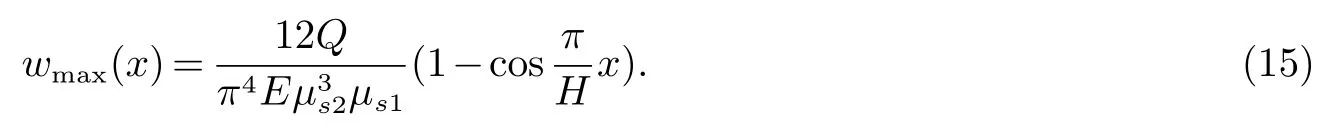
若考虑风载荷为脉动风，具有周期性，表示为q(t)=Qcosωt，其中Q为常量，则可设φ(t)=acos(ψ+ωt)，其中ω=ω0+ε0，代入（11）式有

根据上式可求解ψ和，则代入梁单元的振动响应表达式，得到

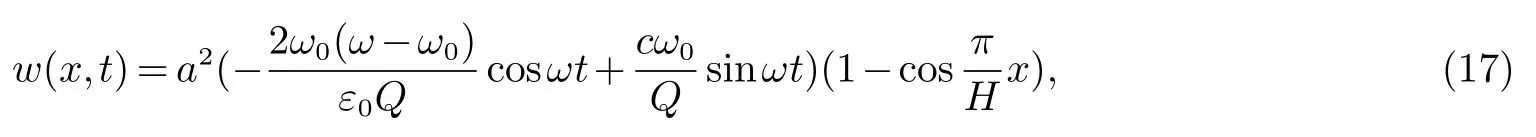
其中

(17)式说明纵向悬臂梁的挠度随时间周期变化，因此结构物沿纵向梁单元的最大挠度为

由此可见，梁单元的最大挠度不仅对结构的体形系数敏感，而且与脉动载荷的周期ω密切相关.

3 结果与分析

选取不同体型系数的矩形截面高层建筑进行研究，建筑物高度均为H=100 m，给定材料参数如下[14]

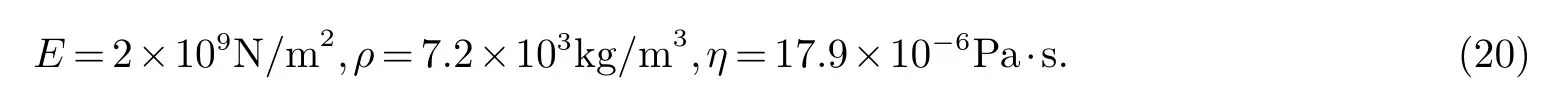
分别给出结构在定常风载荷和脉动载荷下的振动响应结果.

3.1 定常载荷算例

对于图1所示的均质等截面Euler悬臂梁，给定平均风载Q=400kN/m，根据(15)式可求解在定常载荷作用下梁中性面沿w方向的位移，该位移随梁单元高度的变化如图2所示.由图2可知，在定常载荷作用下，相同的迎风面体型系数，结构侧风面体型系数越大，即高宽比越小，其最大水平向位移越小(见图2(a))；而在定常载荷作用下，对于相同的侧风面体型系数，结构迎风面高宽比越小，其最大水平向位移也越小(见图2(b))；相比之下，结构的最大位移随结构侧风面高宽比的变化更加明显.

图2 定常载荷下结构中性面沿水平向的位移随形体比例的变化

关于高层建筑舒适度的测评，一种非常直观的标准就是大风季节实测的高楼楼顶层风致摆动的最大振幅[15]，即顶层中心点的最大风致偏移量保持在H/500以内的高楼可被认为是设计良好的.而在图2中，顶层中心点的风致偏移量均超过0.2 m，换言之，即使不威胁到结构安全，也需要采取措施减小建筑物摆动量以避免不适.

3.2 周期载荷算例

对所讨论的均质等截面Euler悬臂梁，给定脉动载荷幅值Q=400kN/m，代入(19)式，不同载荷周期下结构物沿纵向梁单元的最大挠度随结构体型系数的变化如图3所示.由图3可知,在周期载荷作用下，给定迎风面高宽比，结构的最大水平向位移并不一味随侧风面高宽比单调变化(如图3(a))；而在固定的侧风面高宽比下，结构的最大水平向位移随迎风面高宽比单调递增；相比之下，结构的最大位移随结构侧风面高宽比的变化更加明显；此外，给定侧风面体型系数，结构物沿纵向梁单元的最大挠度会随着激励频率的增大而降低，如图3(b)，图3(d)和图3(f)；其中图3(f)中的部分顶层中心点的风致偏移量已明显控制在0.2 m以内，这也说明激励频率的增大对结构物舒适度起到一定的改善作用.

图3 周期载荷下结构中性面沿水平向的位移随形体比例的变化

4 结果与讨论

通过应用结构静力分析和振动理论研究了一类矩形高层结构物的外观形体比例对风载作用结构的顺风向振动的影响，具体结论如下：

(1)在定常载荷作用下，结构的最大水平向位移随迎风面和侧风面高宽比增大而增大；相比之下，最大顺风向位移随侧风面高宽比的变化更加明显；

(2)作用在结构物上的脉动风会引起顺风向振动：在周期载荷作用下，结构的最大水平向位移并不随侧风面高宽比单调变化,却随迎风面高宽比单调递增，相比之下随结构侧风面高宽比的变化更明显；

(3)在周期载荷作用下，给定侧风面体型系数，结构物沿纵向梁单元的最大挠度会随着激励频率的增大而降低；

(4)在对建筑抗风体型进行优化时，可通过降低迎风面高宽比或调整侧风面高宽比以减小结构的顺风向振动响应的目的.

文章仅考虑了风载对结构的顺风向效应，且对脉动风并未采取风速功率谱等统计分析，与工程实际尚有一定距离.对于高层建筑结构物，还应当进一步考虑上述的脉动风荷载对于建筑结构物的横风向效应和风致扭转效应.此外，目前对存在凹凸的矩形建筑，其风载取值目前一般仍套用标准矩形的风压体型系数，而建筑表面不同凹凸构造显然会对风荷载产生影响，其影响程度也是值得研究的问题.