隐匿顶点数和边数的保密图形相似性判定∗
2018-10-29于宝华巩林明
于宝华,巩林明
0 引言
随着人类信息社会的发展和分布式系统用户对隐私保护需求的日益增长,安全多方几何计算(Secure Multi-party Geometric Computation,SMGC)已经成为安全多方计算中一个新兴的研究领域[1].SMGC主要研究保密几何图形的安全计算问题或安全分析问题,目的是在互不信任的分布式用户间实现协同完成某些特定的计算几何计算任务,同时还要保护参与计算几何协同运算任务各用户的隐私.能够满足分布式用户隐私保护需求的计算几何问题有着重要的应用前景.
作为安全多方计算的热点问题之一,SMGC已经取得了相当成果[1−25].安全几何计算问题最初由Du等人[1,2]提出,并在文献[1,2]中提出了安全两方点包含问题、安全两方线段相交问题、安全两方凸多边形相交问题以及安全两方点的凸壳包含问题的解决方案;文献[9,10,23]在Du的基础上深入研究了安全两方点包含问题;文献[7]研究了保密凸壳挖掘问题;文献[8]研究了保密凸壳相交问题;文献[5]与[6]研究了保密多边形的相交问题;文献[12]研究了两方立体几何安全计算问题;文献[13]究了密态几何信息匹配问题;文献[14]研究了保密三点张成面积计算问题;文献[15]研究了过两私有保密做一条直线问题;文献[16]研究了隐匿拓扑关系的图形计算问题;文献[17]研究了保密空间图形位置关系判定问题;文献[18]研究了借助云计算的保密空间图形位置关系判定问题;文献[19]研究了基于点积保密计算的保密几何计算问题;文献[20]研究了基于保密点积计算的保密特殊多边形相似判定问题;文献[21]研究了基于hash函数的安全两方保密图形相似判定问题.
综述所述,对于分布式环境中一些保护用户隐私的安全几何计算和安全几何分析问题的相关研究已经取得了长足进步,但关于保密图形相似问题的安全几何计算问题尚属初步,例如关于图形相似关系的分析问题仅限于上面论述的问题;现有的保密图形相似判定协议必须基于一个前提:双方边向量维数、角向量维数以及邻接矩阵维数对应相等,也就是说,双方在进行保密计算之前就已经知道对方图形的顶点数和边数.关于隐匿顶点数和边数的保密几何图形相似计算和分析问题尚未研究.然而,隐匿顶点数和边数的保密几何图形相似判定在保密地理信息查询系统[24]和社交网络用户近感查询系统[25]中更具有现实的应用价值.因为如果采用现有的保密图形相似判定协议解决地理信息系统以及社交网络中的用户隐私保护问题会造成先发送(哪怕是加密的)消息一方信息的泄露:先得到消息的一方会通过接收(哪怕是加密的)消息的数量事先得知另一方的边、角、顶点个数,要知道这些信息都有助于图形形状的判定,而形状对基于图形相似判定的地理信息系统保密信息匹配至关重要,例如,地理信息系统中可能存在多个地理区域边数唯一的情形.此外,如果查询信息不匹配,双方还可以得知是对应边不成比例、或是对应角不相等、亦或是图不同构影响着不相似的结果,泄露了不该泄露的信息.因此,隐匿图形顶点数和边数的保密图形相似性判定问题亟待研究.
本文主要研究隐匿顶点数和边数的保密图形相似性判定问题,隐匿参与方图形顶点数和边数的核心问题是如何实现隐匿维数的保密向量运算.主要贡献如下:
(1)提出一种隐匿向量维数的保密向量操作方法,该方法不仅可以用于解决隐匿向量维数的保密向量相等判定和保密向量对应分量成比例判定等问题,还可以用于解决隐匿集合势的保密集合相等问题;
(2)采用布尔矩阵的向量编码方法、隐匿向量位数的保密向量操作方法和Paillier同态加密方案设计了隐匿顶点数和边数的保密图形相似性判定协议.解决了隐匿顶点数和边数的保密图形相似性判定这一公开问题.
1 预备知识
1.1 关于安全多方计算协议的安全性定义
定义 1文献[3]中关于一个安全多方计算协议的安全性定义如下:对于概率多项式函数f,协议π可以保密地计算f(a,b)如果存在概率多项式时间模拟算法S1与S2使得
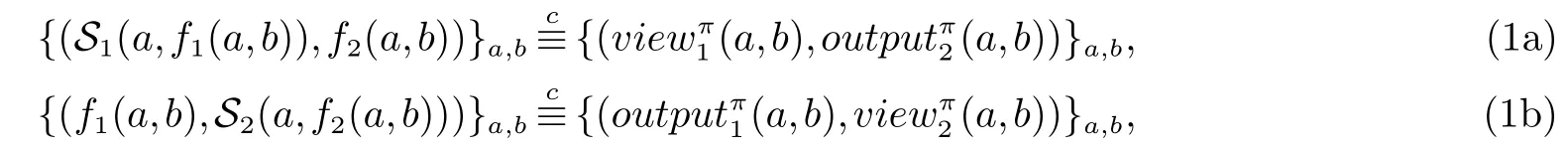
1.2 Paillier变体同态加密方案
本文设计的协议采用Gong等人[15]提出的Paillier变体同态加密方案,在此将其概述为:
(1)符号记法:p与q是大素数,|p|=|q|,n=pq,λ=lcm(p−1,q−1),g=1+n,;
(2)加密:对于明文m (3)对于密文对(c1,c2),其中c1,c2 该方案不仅保持了良好的加法同态性E(x+y)=E(x)·E(y),E(x×y)=Ey(x)=Ex(y)而且还具有加密底数可以由无密钥一方计算的良好性质(此性质在安全多方计算中可以确保无密钥一方私有数据的安全性).该方案在高阶剩余类判定性困难假设下,具有选择明文攻击不可区分安全性[4],即,其中c0与c1分别是明文m0与m1对应的密文. 以下四个协议的设计采用的数学常识为: 设P(·,·)是谓词函数给定有理数0整数θ1,θ2∈Zn则有成立.反之,如果那么必有 隐匿边数和顶点数的保密图形同构判定问题实质是隐匿矩阵维数的保密图形对应邻接矩阵相等判定问题.为了解决隐匿边数和顶点数的保密图形同构判定问题,本节采用布尔矩阵的向量表示方法先将图形的邻接矩阵表示成向量,然后采用隐匿维数的保密向量运算方法解决隐匿边数和顶点数的保密图形同构判定问题. 2.1.1 协议Π1:保密图形的同构判定协议 输出:P(Ma,Mb). Step 1.Alice先运行Paillier变体方案的密钥生成算法产生公私钥:公钥Kpub=(n,g=1+kn),私钥λ; Step 2:Alice和Bob分别按照下述步骤1)和2)工作: 1)公布公钥后,Alice按照如下方式执行协议:(1)采用布尔矩阵的向量表示法将其私有图形对应的邻接矩阵Ma表示成向量µa←(µ1,µ2,···,µka); (2)对于1≤i≤ka,计算ka个分向量µi对应的密文modn2; (3)选择一个随机数k1(满足计算k1个1的密文modn2,其中ka (4)将密文元组(cµ1,cµ2,...,cµk1+ka)发送给Bob. 2)在Alice加密的同时,Bob按照如下方式执行: (1)采用布尔矩阵的向量表示法将其私有邻接矩阵Mb表示成向量νb←(ν1,ν2,···,νkb); (2)对于1≤i≤kb,计算kb个分向量νi对应的密文modn2; (3)选择一个随机数2k2+k1+ka−kb¿n(满足kb+k2+k1−ka>0),计算2k2+k1+ka−kb个密文modn2,其中1≤j≤k2; Step 3.收到(cµ1,cµ2,...,cµk1+ka)后,Bob按照如下方式执行: (1)对于1≤i≤k1+ka,分别对(cµ1,cµ2,...,cµk1+ka)对应的k1+ka个密文分量执行同态操作: (2)将Step 2中Bob 已经计算好的2k2+k1+ka−kb个密文modn2,其中1≤j≤2k2+k1+ka−kb)中的k2个添加到密文组(cµ1,cµ2,...,cµk1+ka)之后,剩余的k2+k1+ka−kb个添加到密文组(cν1,cν2,...,cνkb)之后,从而得到两个新的、等长的有序密文元组,分别记作:(cµ1,cµ2,...,cµk1+k2+ka)和(cν1,cν2,...,cνk1+k2+ka); (3)按照如下方式随机组织密文对: i将cµi∈(cµ1,cµ2,...,cµk1+k2+ka)和cν1∈(cν1,cν2,...,cνk1+k2+ka)分别作为第一和第二分量构造二元组 ii对(cµ1,cν1),(cµ2,cν2),...,(cµk1+k2+ka,cνk1+k2+ka)在对内做随机置换; iii将上一步得到的密文对再做对间的随机置换,并将得到新的密文对序列记作: Step 4.Alice收到后按照如下方式进行: 2.1.2 协议Π1的保密性 定理 1在半诚实模型下,协议Π1能够保密地判定两个图形是否同构. 证明Π1是Alice和Bob协同计算函数:P(Ma,Mb)的协议,其中他们的输入分别为各自图形的邻接矩阵:与. 下面我们将构造符合1.1节中式(1a)和式(1b)的模拟器 Alice在执行协议Π1的过程中视图(view)记为: Alice执行协议后的输出记为: 下面构造模拟器模拟Alice的视图. 以及Bob的私有图形Mb,其中则有: 从模拟器收到后,Bob按照如下方式执行: (1)对于1≤i≤k1+ka,分别对对应的k1+ka个密文分量执行同态操作: (2)将先前已经计算好的2k2+k1+ka−kb个密文modn2,其中1≤j≤2k2+k1+ka−kb)中的k2个添加到密文组之后,剩余的k2+k1+ka−kb个添加到密文组之后,从而得到两个新的、等长的有序密文元组,分别记作 (3)按照如下方式随机组织密文对: iii将上一步得到的密文对再做对间的随机置换,并将得到新的密文对序列记作:和 综上所述,可以构造一个满足: 类似地,也可以构造一个满足: 本节采用隐匿维数的保密向量运算方法解决隐匿边数的保密图形对应边是否成比例判定问题. 2.2.1 协议Π2:对应边是否成比例的保密判定协议 输入:Alice输入边长向量=(a1,a2,...,aka),Bob输入边长向量=(b1,b2,...,bkb),系统安全参数‘(系统中可接受(一方面考虑到协议执行效率)的最大边数)和‘0,其中ka,kb<‘,‘0¿n用于限定双方总共可以引入的随机输入(这些随机输入用于隐藏双方顶点数或边数等信息,但不影响保密计算的结果的正确性). Step 1:Alice先运行Paillier变体方案的密钥生成算法产生公私钥:公钥(n,g=1+kn),私钥λ; Step 2:Alice和Bob分别按照步骤1)和2)执行协议: 1)发布公钥后Alice按照如下方式工作 (1)将有理数形式的边长向量的各分量表示成分数,然后将这些分量的分子和分母分别表示成向量; (2)对于1≤i≤ka,计算2ka个边长对应的密文modn2,其中 (3)选择一个随机数k1(满足计算2k1个1的密文modn2,=modn2,其中 2)在Alice加密的同时,Bob按照如下方式执行: (1)将有理数形式的边长向量的各分量表示成分数,然后将这些分量的分子和分母分别表示成向量 (2)选择一个随机数k2¿n(满足并且k1+ka+k2−kb>0),计算2k2个密文modn2,其中1≤j≤k2. Step 3.收到Alice发来的后,Bob按照如下方式执行: (1)对于1≤i≤kb,分别对的前kb个密文执行同态操作 (2)对于(kb+1)≤i≤(k1+ka),分别对和的后k1+ka−kb个密文执行同态操作 (3)将Step 2中Bob已经计算好的2k2个密文modn2,其中1≤j≤k2)平分成两份,并分别添加到密文组之后,得到两个新的有序密文元组; (4)随机组织密文对: ii先对上步得到的k1+ka+k2个密文对实施对内随机置换; iii对已经实施对内随机置换的k1+ka+k2个密文对再实施对间随机置换,并将得到的密文对序列记作:; Step 4.Alice收到后按照如下方式进行: 2.2.2 协议Π2的私密性 定理 2在半诚实模型下,Alice和Bob利用协议Π2能够保密地判定他们私有图形对应边是否成比例. 证明Π2是Alice和Bob协同计算函数P()的协议,其中他们的输入分别为各自图形的边向量:=(a1,a2,...,aka)与=(b1,b2,...,bkb). 下面我们将构造符合1.1节中式(1a)和式(1b)的模拟器. Alice执行协议Π2时的视图(view)记为: Alice执行协议Π2的输出记为: 下面构造模拟Alice视图的模拟器. 模拟器的输入为:随机选取一个具有个有理分量的向量以及Bob的私有图形对应的边长向量=(b1,b2,...,bkb),其中.则有: (1)对于1≤i≤kb,分别对和的前kb个密文执行同态操作= (2)对于(kb+1)≤i≤(k1+ka),分别对和的后k1+ka−kb个密文执行同态操作上述两步完成后,得到两个新的有序密文元组和 (3)将先前已经计算好的2k2个密文modn2,其中1≤j≤k2)平分成两份,并分别添加到密文组之后,从而得到两个新的有序密文元组 (4)随机组织密文对: ii对k1+ka+k2个密文对实施对内随机置换; iii将上一步得到的密文对再实施对间随机置换,并将得到新的密文对序列记作: 综上所述,可以构造一个满足: 类似地,也可以构造一个满足: 2.3.1 协议Π3:对应角相等与否的保密判定协议 输入:Alice输入角向量∠=(∠A1,∠A2,...,∠Aka),Bob输入角向量∠(∠B1,∠B2,...,∠Bkb). Step 1.Alice先运行Paillier变体方案的密钥生成算法产生公私钥:公钥(n,g=1+kn),私钥λ; Step 2. 1)Alice公布公钥后按照如下方式执行 (1)将有理数形式的边长向量的各分量表示成分数,然后将这些分量的分子和分母分别表示成向量; (2)对于1≤i≤ka,计算2ka个边长对应的密文 (3)选择一个随机数k1(满足计算2k1个1的密文=modn2,其中ka 2)在Alice加密的同时,Bob按照如下方式执行: (1)将有理数形式的边长向量的各分量表示成分数,然后将这些分量的分子和分母分别表示成向量 (2)选择一个随机数k2¿n(满足计算2k2个密文modmodn2,其中1≤j≤k2. Step 3.收到Alice发来的和后,Bob按照如下方式执行: (1)对于1≤i≤kb,分别对的前kb个密文执行同态操作modn2=modn2; (2)对于(kb+1)≤i≤(k1+ka),分别对的后k1+ka−kb个密文执行同态操作modn2=(1+modn2;由上述两步得到两个新的有序密文元组; (3)将先前Step 2中已经计算出的2k2个密文其中ka (4)随机组织密文对: iii再对上一步得到的密文对实施对间随机置换,并将得到新的密文对序列记作: Step 4.Alice收到后按照如下方式进行: 2.3.2 协议Π3的保密性 定理 3在半诚实模型下,协议Π3能够保密地判定两个图形对应角是否相等. 证明:Π3是Alice和Bob协同计算函数P(∠∠)的协议,其中他们的输入分别为各自图形的角向量:∠=(∠A1,∠A2,...,∠Aka)与∠=(∠B1,∠B2,...,∠Bkb). 本定理以下部分的证明和定理2基本上一样,为了节省篇幅在此不再赘述.采用定理2的构造方法构造模拟器满足: 保密图形相似性判定问题:Alice和Bob分别有一个私有图形Ga与Gb,二人想协同判定两个图形是否相似,但不泄露各自的顶点数或边数在内的图形信息(边、角、邻接矩阵).协议的基本思想:协议Π4同时调用协议Π1、Π2和Π3,实现保密图形相似性判定. 双方如何形成相同的图形拓扑关系,即构成对应边、对应角和对应矩阵:双方保密图形的对应需要根据实际应用而定,比方说在保密地理信息匹配应用中可以指定某个地点所在的边为起始边,然后按照该地点的南向为逆时针走向的起始方向依次编排边向量.以下都假定双方已经在具体应用中已经确定了图形的拓扑关系. 协议Π4:图形间的相似性保密判定 输入:Alice输入各边长构成的元组(a1,a2,...,aka)、各角大小构成的元组(∠A1,∠A2,...,∠Aka)以及图的邻接矩阵对应的向量表示(µ1,µ2,···,µka);Bob输入边长向量(b1,b2,...,bkb)、角向量(∠B1,∠B2,...,∠Bkb)以及图的邻接矩阵对应的向量表示(ν1,ν2,···,νkb);系统安全参数‘(系统中可接受(一方面考虑到协议执行效率)的最大边数)和‘0,其中ka,kb<‘,‘0¿n用于限定双方总共可以引入的随机输入(这些随机输入用于隐藏双方顶点数或边数等信息,但不影响保密计算结果的正确性). 输出:如果两个图形相似,则置T=1,否则,置T=0. Step 1:输入安全参数1n,‘,‘0; Step 2:调用协议1、协议2和协议3,并计算+P(Ma,Mb); 协议Π4的保密性 定理 4在半诚实模型下,如果协议Π1、Π2以及Π3能够各自的保密计算任务,则协议Π4能够实现保密图形相似性判定. 证明协议Π4实质是Alice和Bob协作保密计算=P()+P(∠∠)+P(Ma,Mb).这就是说,协议Π4的私密性完全依由协议Π1、Π2和Π3决定,考量Π4的私密性就是要看计算P()、P(∠∠)和P(Ma,Mb))时,有无造成Alice和Bob双方信息泄露. 因为我们已经证明:在半诚实模型下,协议Π1能够保密判定两个图形是否同构、Π2能够保密判定两个图形对应边是否成比例、Π3能够保密判定两个图形的对应角是否相等;即协议Π4的输入P()、P(∠∠)与P(Ma,Mb)没有造成参与各方信息的泄露,所以采用Π4计算=P()+P(∠∠)+P(Ma,Mb)不会造成Alice和Bob双方私有图形信息的泄露.因此,定理4成立. 本文研究的是隐匿顶点数和边数的保密图形判定问题,在此之前没有这方面的研究,因此在效率方面与先前的保密图形相似判定协议不具有可比性.在安全性方面,最新研究成果[21]虽然很好地解决了图形相似判定问题中的隐私保护问题,我们发现以hash函数抗碰撞性做为用户信息安全的保障保密图形相似协议的安全性还可以进一步提高:hash函数通常被用于信息认证和数字签名中,通常将非定长信息映射为定长信息,而成果[21]中用hash函数将定长图形信息映射为另一定长信息,这种情形难于抵抗攻击者暴力破解图形私密信息;而本文采用基于高阶剩余类困难问题Paillier变体同态加密方案为保密工具,可以抵抗敌手暴力破解图形私密信息;此外,协议[21]只适用于解决顶点数相同,即协议执行之初就已经泄露了参与方的顶点数、边数信息,而本文协议不会造成参与各方顶点数、边数信息的泄露.表1是协议[21]和本文协议在保密向量操作是否泄露向量的维数、解决问题的程度(以隐匿顶点数和边数体现)以及二者所采用的保密工具三个方面的对比: 表1 本文协议与协议[21]的对比分析 本文首先设计一种隐匿向量维数的保密向量操作方法,然后采用这两种方法与Paillier同态变体加密方案,设计了一个隐匿双方顶点数和边数的保密图形相似判定协议.该协议由隐匿邻接矩阵维数的保密图形同构判定协议、隐匿顶点数的保密图形对应角相等判定协议和隐匿边数的保密图形对应边成比例判定协议三个子协议组成.较之于采用Hash函数设计的协议,本文设计的协议具有隐匿顶点数的优点,更符合地理信息系统和社交网络用户隐私保护的需求.2 图形间的相似性判定
2.1 保密图形的同构判定问题
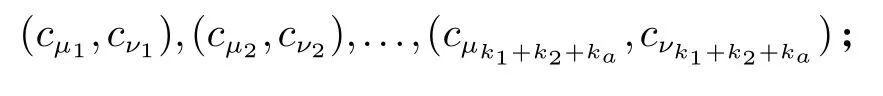
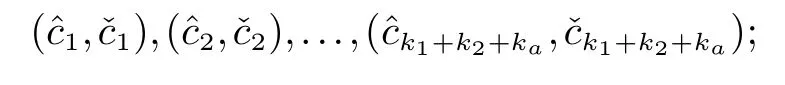

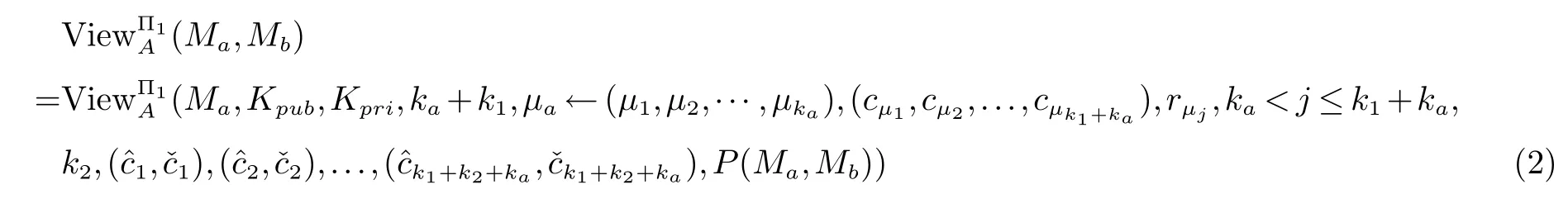
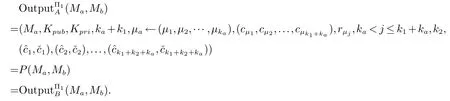
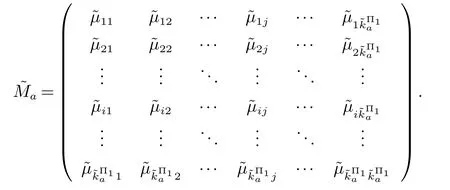
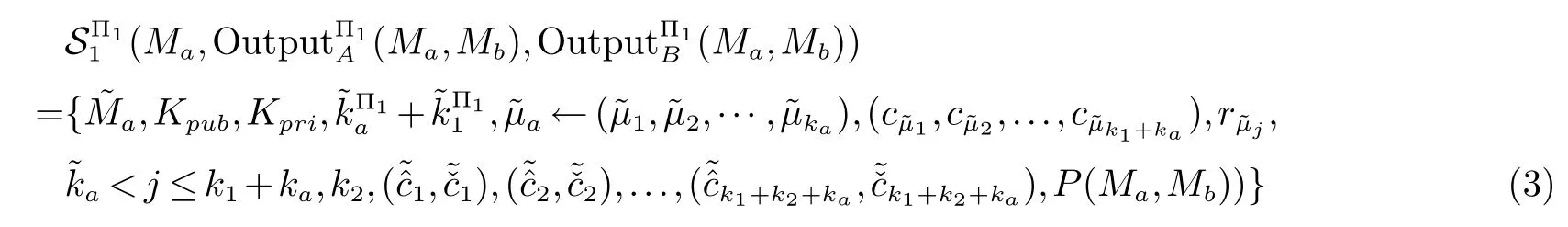
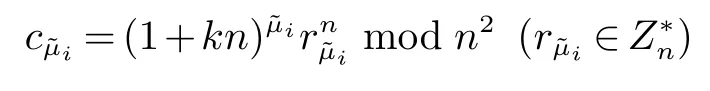
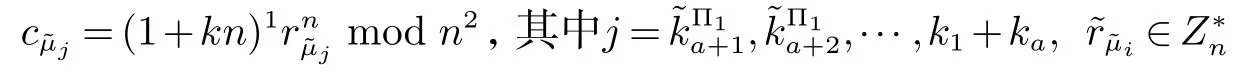
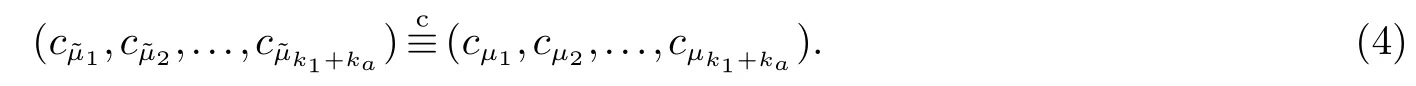
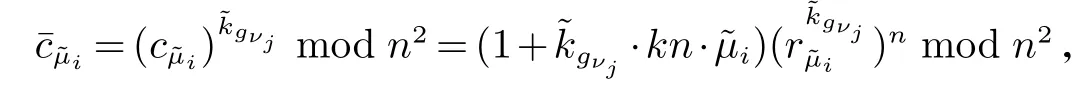
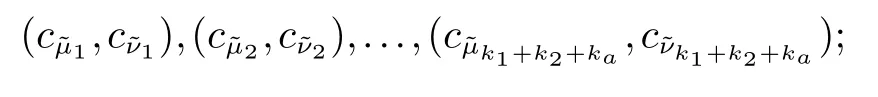
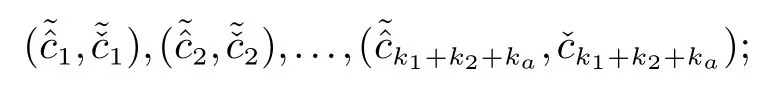
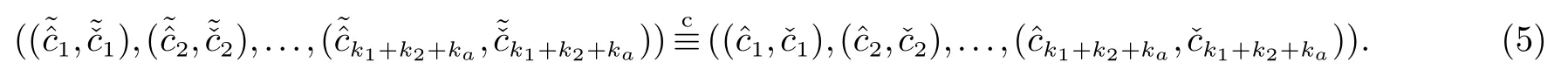
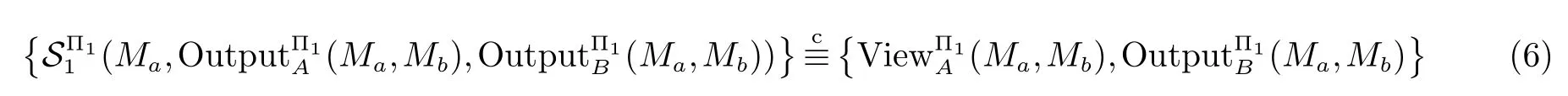
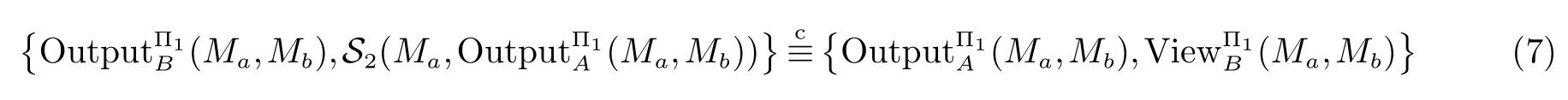
2.2 两图形对应边成比例与否的保密判定

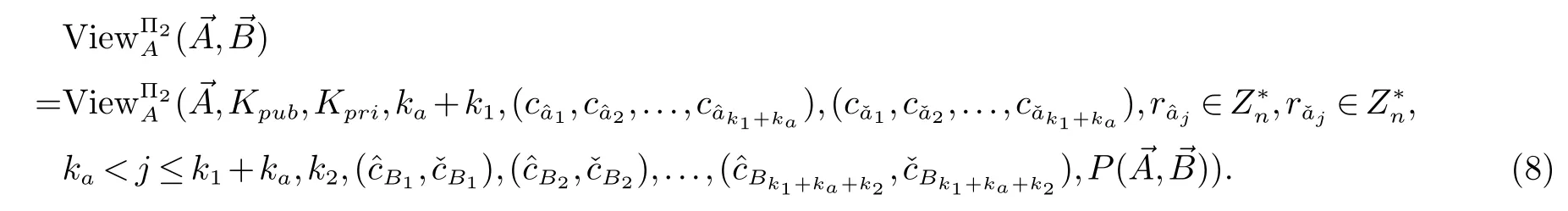
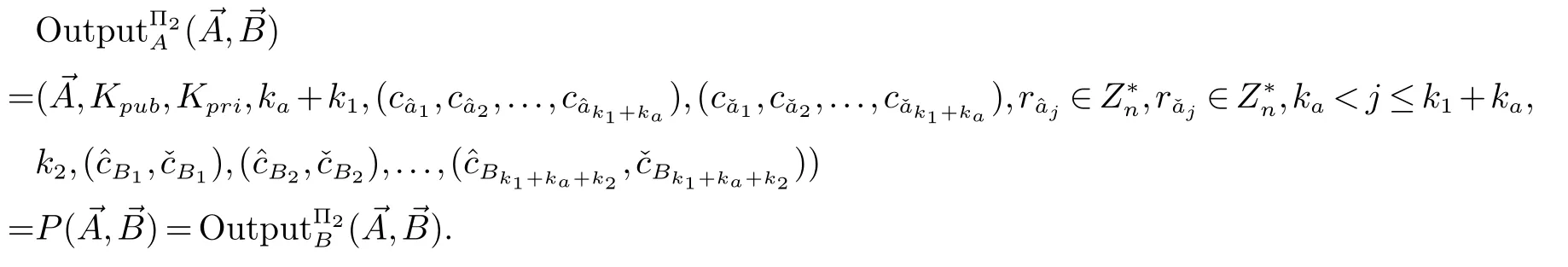
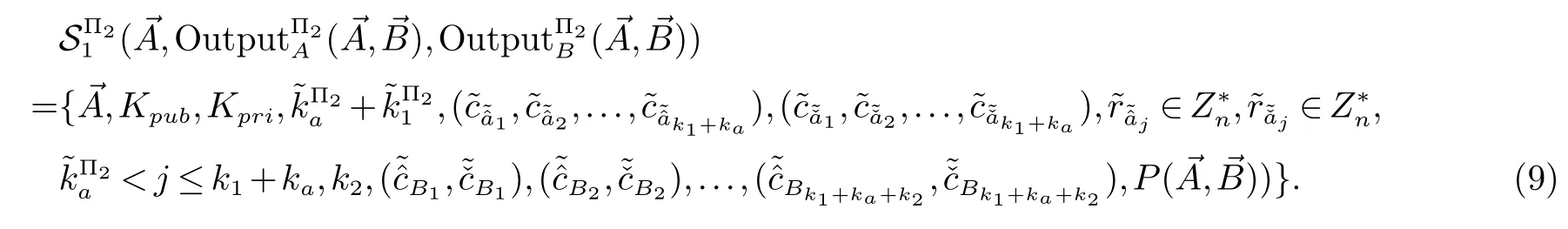
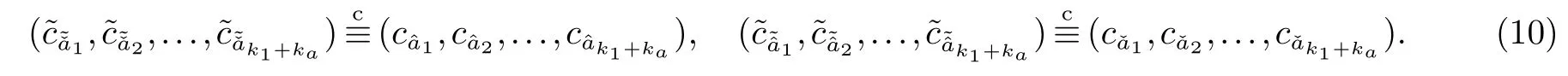
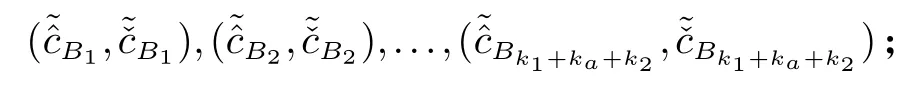
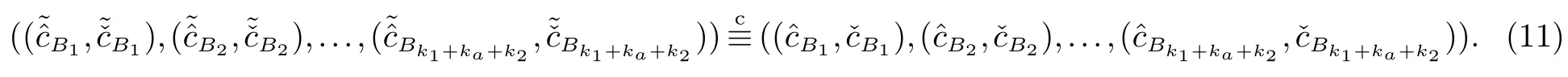
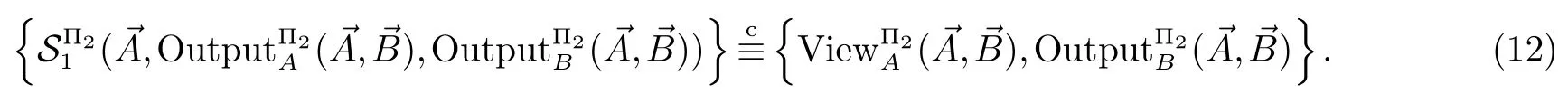
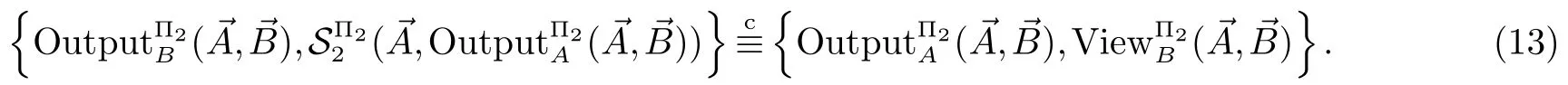
2.3 对应角相等与否的保密判定问题
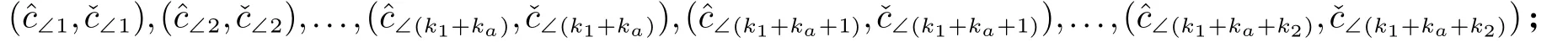
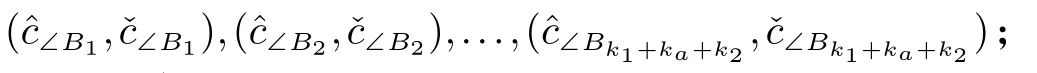
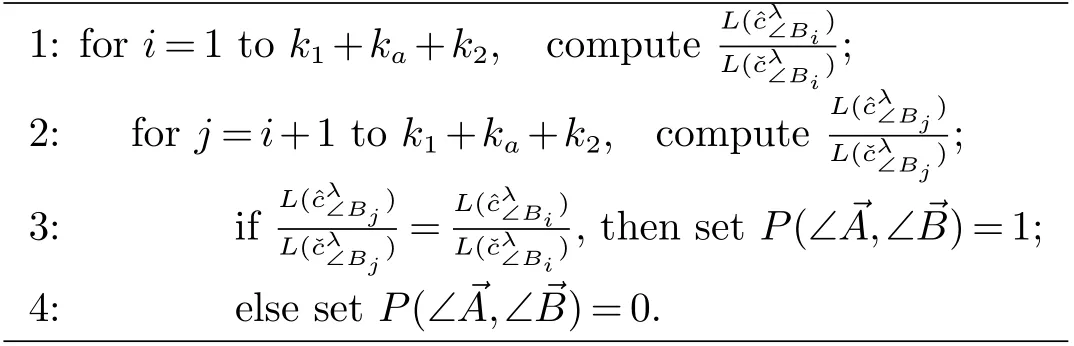

2.4 图形间的相似性判定
3 性能对比分析

4 结束语
