点目标防御武器配系部署规划
2018-10-29刘瑶张占月黄梓宸赵程亮
刘瑶,张占月,黄梓宸,赵程亮
(航天工程大学a.研究生院;b.太空安全研究中心,北京 101416)
0 引言
在以战略威慑与精确打击主导的现代化、信息化战争中,弹道导弹已经成为影响战场态势、决定战场胜负的重要因素[1]。为有效保卫重要资产安全,需将反导武器进行优化配置使得在有限的作战资源条件下,尽可能的发挥反导武器的作战效能。
国内对防空反导武器的部署进行了相关研究,文献[2-5]针对末端反导建立了兵力需求优化模型,提出了地空导弹武器系统反TBM有效部署区的概念,建立了部署的数学模型。文献[6]针对防空火力配系,为解决火力协同和战斗优化问题,建立了评估火力配系效果的模型。文献[7]针对反导杀伤区变化的原因,给出了特殊情形下反导杀伤区变化的分析方法。
本文依据中段反导的特点并结合末段反导和防空的理论,选取某一中段反导武器对其防护区进行了分析。并分别对单一方向威胁目标和扇形区域方向的威胁目标2种作战场景下的反导部署建立了相关的理论模型,并应用遗传算法对扇形威胁下的作战部署模型进行了优化。
1 反导防护区和部署区
火力单元的防护区定义为由于反导系统对来袭弹道导弹进行拦截使得地面资产受毁伤的区域,它是弹道导弹通过反导火力单元杀伤区落点构成的区域[8]。文献[9]中将反导系统对地面防护区进行了解析描述。如下图1所示。
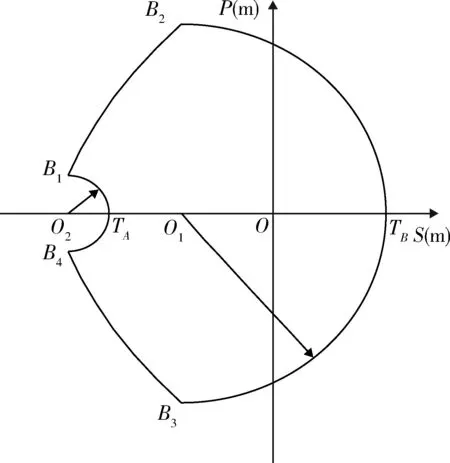
图1 反导系统对地面的防护区Fig.1 Protection zone of missile defense system on the ground
图1中O点为反导系统的部署位置,导弹的来袭方向沿着S轴的负方向,曲线B1B2TBB3B4TA包围的区域即为反导系统的防护区。
反导系统的防护区可以表征其防御范围的大小,其大小形状对反导作战的阵地部署和火力分配有着直接的影响。反导防护区与反导系统自身的拦截范围,来袭目标方向,弹道轨迹息息相关,防护区的大小形状会随着来袭弹道导弹特性的不同而改变,并且在拦截弹防护区内不同位置处的防护能力是不同的。
在明确被保卫地面资产之后,应该使被保卫地面资产处于反导系统的有效防护区内。假设反导系统对来袭弹道导弹目标的单发拦截概率是固定值,防护区内不同位置点的不同防御效能可以用反导系统对来袭弹道导弹目标拦截纵深的大小来衡量,拦截纵深的大小即可拦截弧段的长度,长度越长说明反导系统可以选择的拦截点越多,能够根据实际作战情况选择最佳的拦截点,并且拦截弧段越长可以为二次拦截提供更长的拦截时间窗口。
部署区[10]定义为针对某个确定的被保卫地面资产以及威胁,能够使得被保卫地面资产在拦截弹防护区内的拦截弹阵地的部署区域。由此可以看出拦截弹的防护区和部署区紧密相关。将防御区和有效部署区的关联性进行了分析,即拦截弹防护区模型中将拦截弹阵地部署点与被保卫目标位置进行一一交换,便得到了针对某一被保卫地面资产和威胁方向时,拦截弹的部署区。如图2所示。
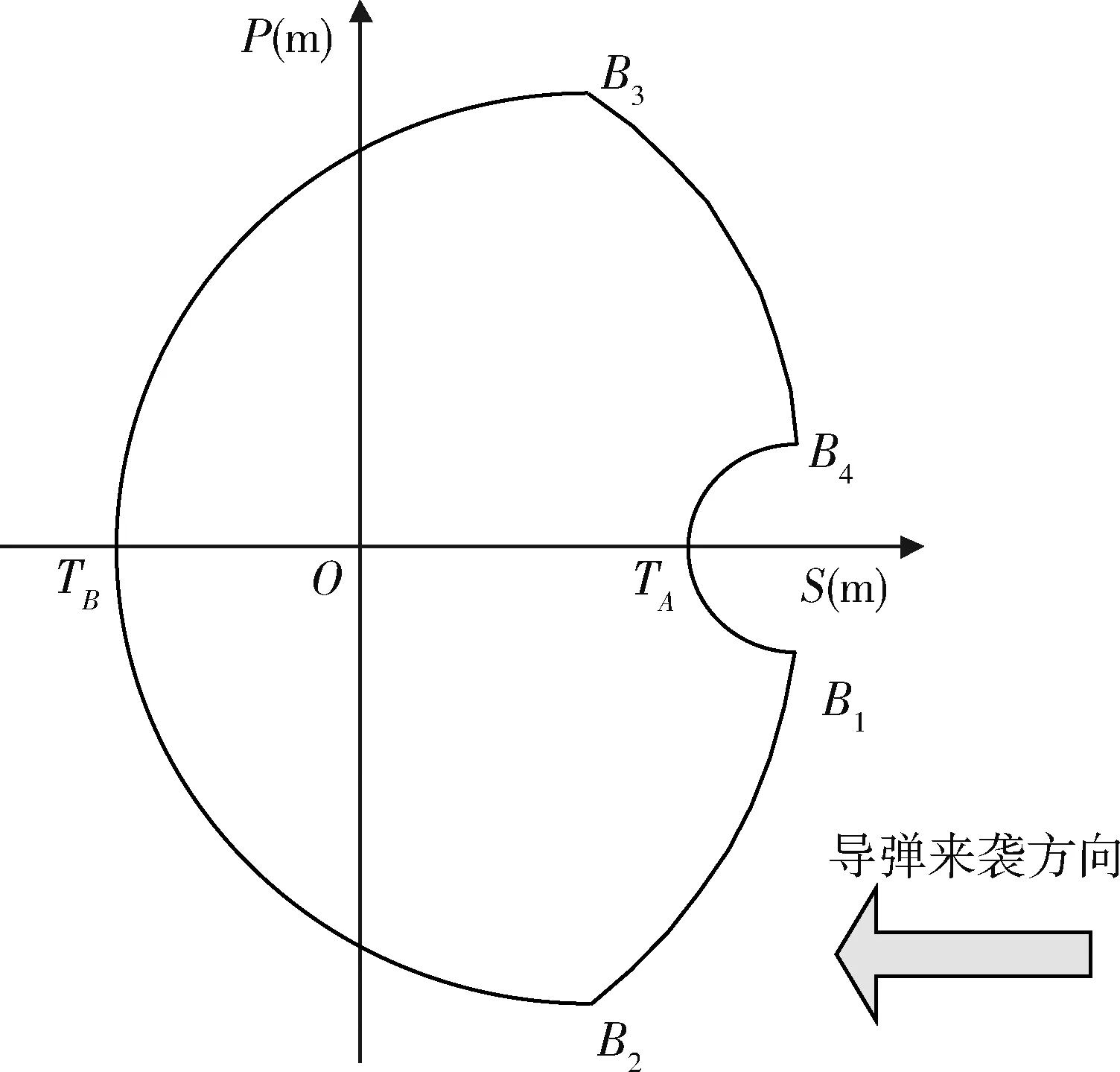
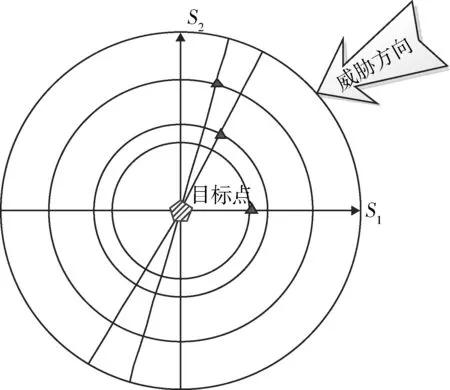
图2 拦截弹阵地的部署区Fig.2 Deployment area of the interceptor position
图2中O点为被保卫地面资产中心点位置。针对图中箭头所指导弹来袭方向,拦截弹部署在图中闭合曲线保卫区域内时,能够使得被保卫地面资产在拦截弹的防护区内。
2 威胁分析和作战想定
在进行反导作战的过程中,首先要对敌我态势进行分析。针对我方要保卫的某一个确定的地面资产,其威胁方向是单方向的或者是多方向的一个扇形范围,在明确威胁方向后,要对敌方可能采用的进攻策略进行分析。针对敌方任何一种形式的进攻作战方式,保卫方都能及时采取合适的应对措施,是决策者追求的理想的作战规则。这就要求针对敌方任何可能的进攻方案做出相应的对策,以便在实战中能够尽快实施。本文中针对敌方最可能的进攻方案做出最可能作战想定,针对不确定的进攻方案做出最坏作战想定[11]。
中段反导作战属于战略性防御作战,其防御目标一般为中远程导弹或者是洲际导弹。最可能的想定分析为:针对某一地面资产,威胁方向为单一的某一个可能的进攻方向,来袭弹道导弹的类型基本可以确定。最坏作战想定为:在一次进攻中敌方使用的导弹的型号,采用的进攻策略,是多发齐射还是间隔发射,什么时间进攻,采用什么样的突防措施,来袭弹道导弹的方向等是不确定因素,威胁方向为一个大角度扇形范围。
3 单方向威胁的中段反导武器部署
针对单方向的来袭弹道导弹威胁,对于每个目标如果采用“一打一”的拦截方式,假设拦截弹的单发命中率是定值,则以拦截纵深作为判断拦截弹对目标的综合拦截效能,拦截纵深越大综合拦截效能越大。
选取某一型号的弹道导弹和拦截弹,拦截弹在空间中的杀伤区如图3所示。
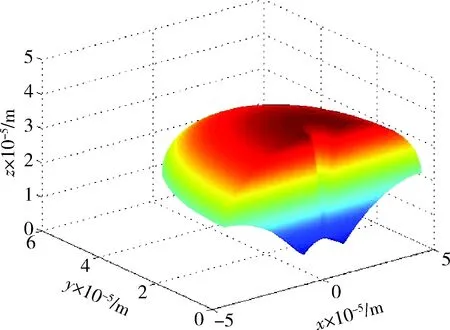
图3 拦截弹在空间中的杀伤区Fig.3 Space of the killing zone of the interceptor
弹道导弹在地心固连坐标系(ECEF)的轨迹如图4所示。
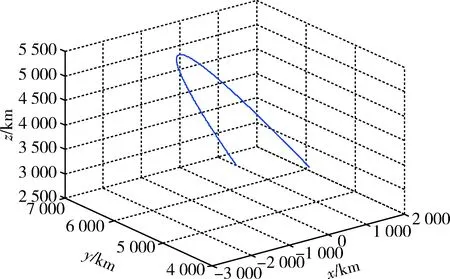
图4 来袭弹道导弹轨迹Fig.4 Incoming missile trajectory
用一个包围图1中的防护区的最小矩形进行等间隔离散化,选取步长为10 km,由于区域的对称性,取一半的区域求解拦截纵深,如图5所示。
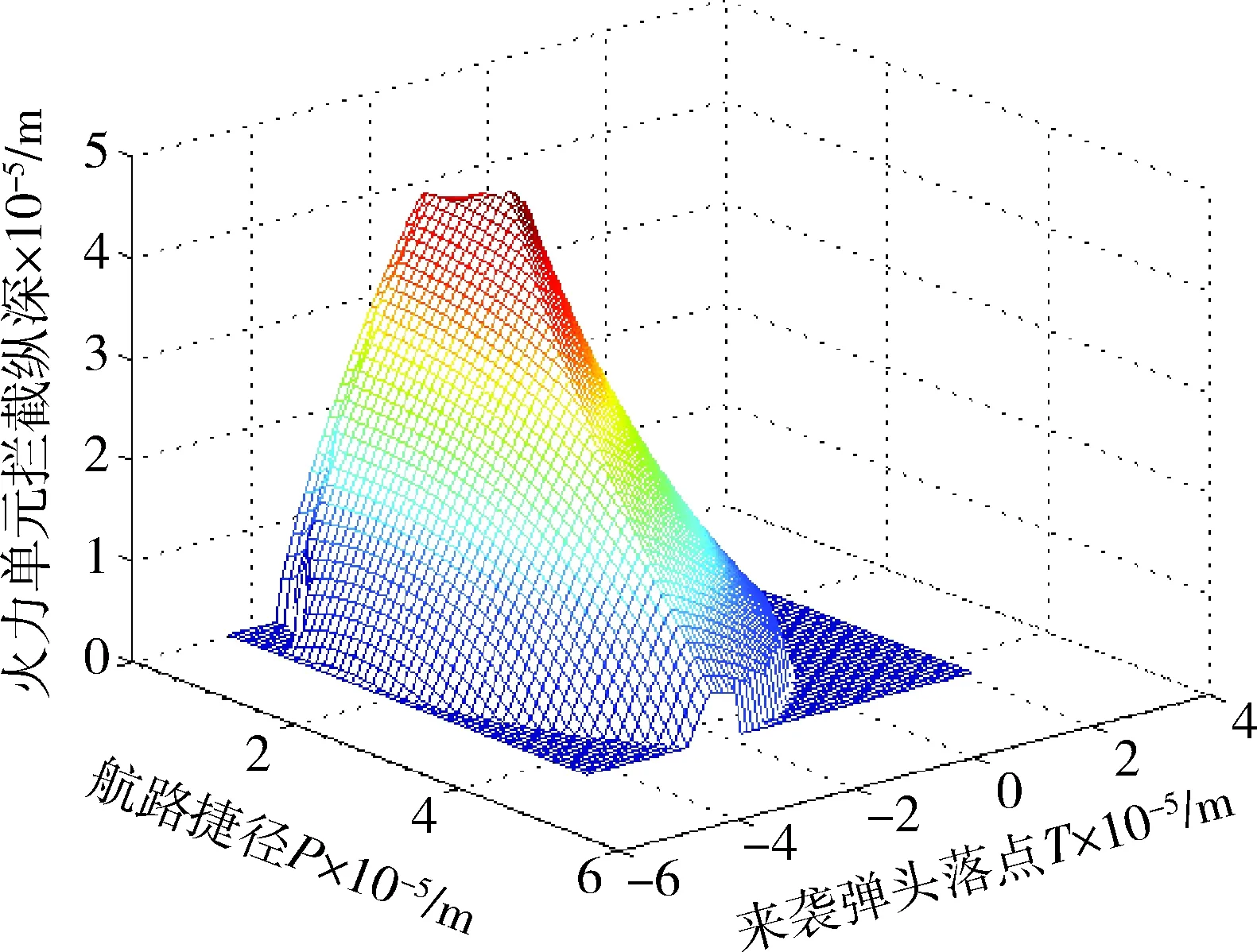
图5 防护区内不同位置的拦截纵深Fig.5 Depth of interception in different locations within the protected area
由图5可知反导系统在防护区外的位置,拦截纵深为0,在防护区内的位置拦截纵深会随着位置的不同而变化。当导弹落点在(90 000,-81 900)m时,部署在O点火力单元对其拦截纵深最长,最大拦截纵深为411 300 m。
针对此种类型的来袭目标,依据火力单元部署与落点的相对关系可知当落点确定时,在以导弹落点为原点,以来袭弹道导弹的攻击方向的反向为极坐标0°的坐标系中,使得拦截纵深最大的火力单元部署的位置为(121 690 m,137.7°)。
4 扇形威胁中段反导武器部署
针对重要资产的防御中,在实际作战中,某个保卫的威胁方向可能不唯一,有可能有多个方向, 这就需要在阵地部署的时候要综合考虑多个方向的进攻目标。通过合理的阵地部署使得所保卫目标处于针对各个方向上的火力单元的防护区内。
4.1 拦截弹阵地对所保卫地面资产的防护角
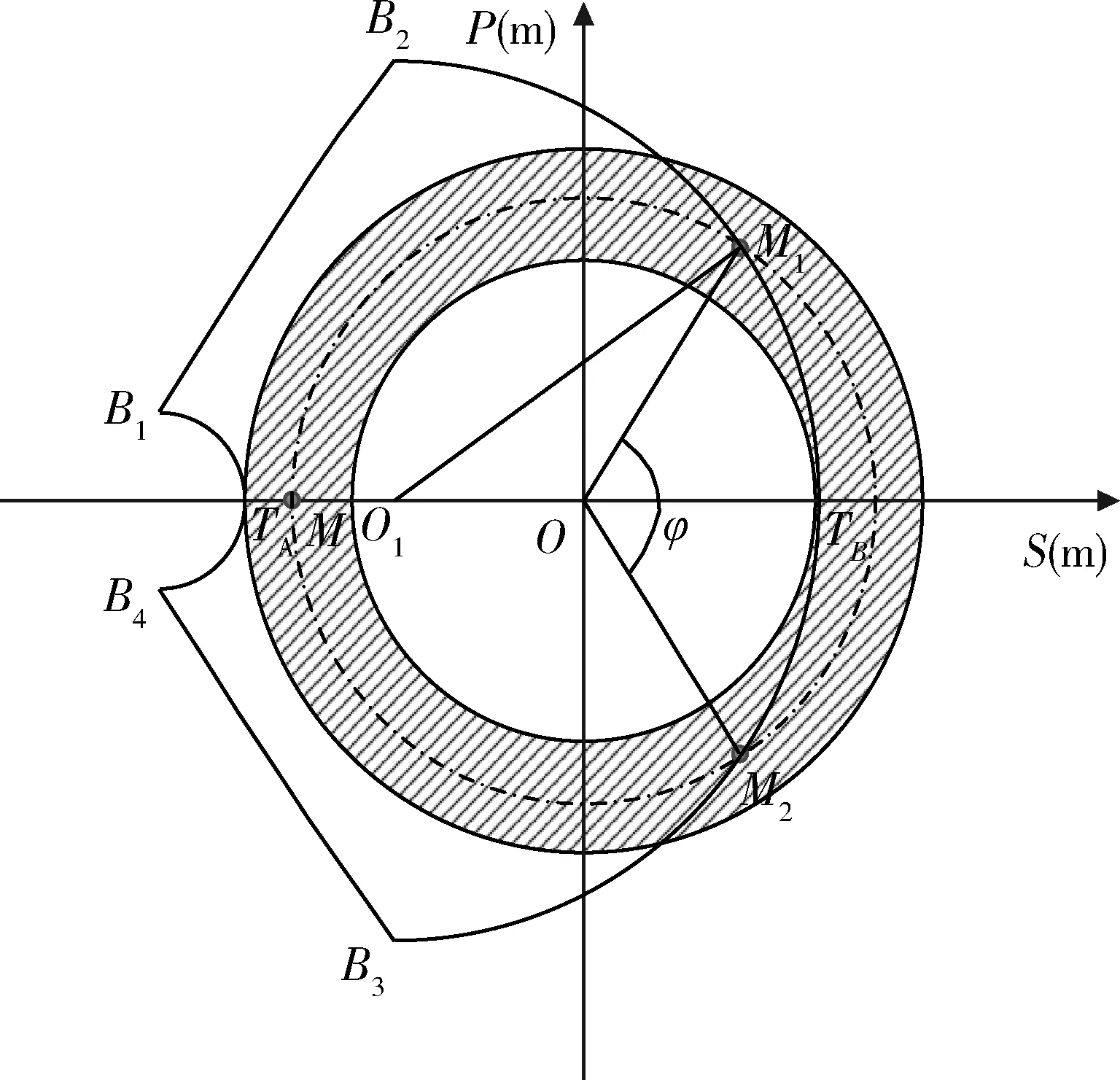
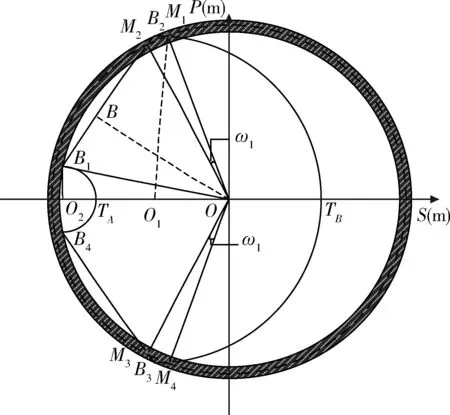
火力单元对保卫地面资产的防护角定义为:反导火力单元对保卫地面资产形成防护能力下,可以抗击来袭弹道导弹方向的角度范围[12]。如图6所示,火力单元部署在O点,保卫目标为M,针对来袭方向为S轴负方向的弹头,当保卫目标在火力单元的防护区内时,火力单元对目标形成防护能力。说明针对保卫目标M,火力单元部署在O点,能够防御来自S轴负方向的威胁。以火力单元部署点为圆心,转动火力单元的防护区,使S轴的负方向始终与威胁方向平行。在不断转动的过程中,目标M在防护区内时,坐标轴转过的角度的集合,即为部署在O点的火力单元对目标M的防护角。
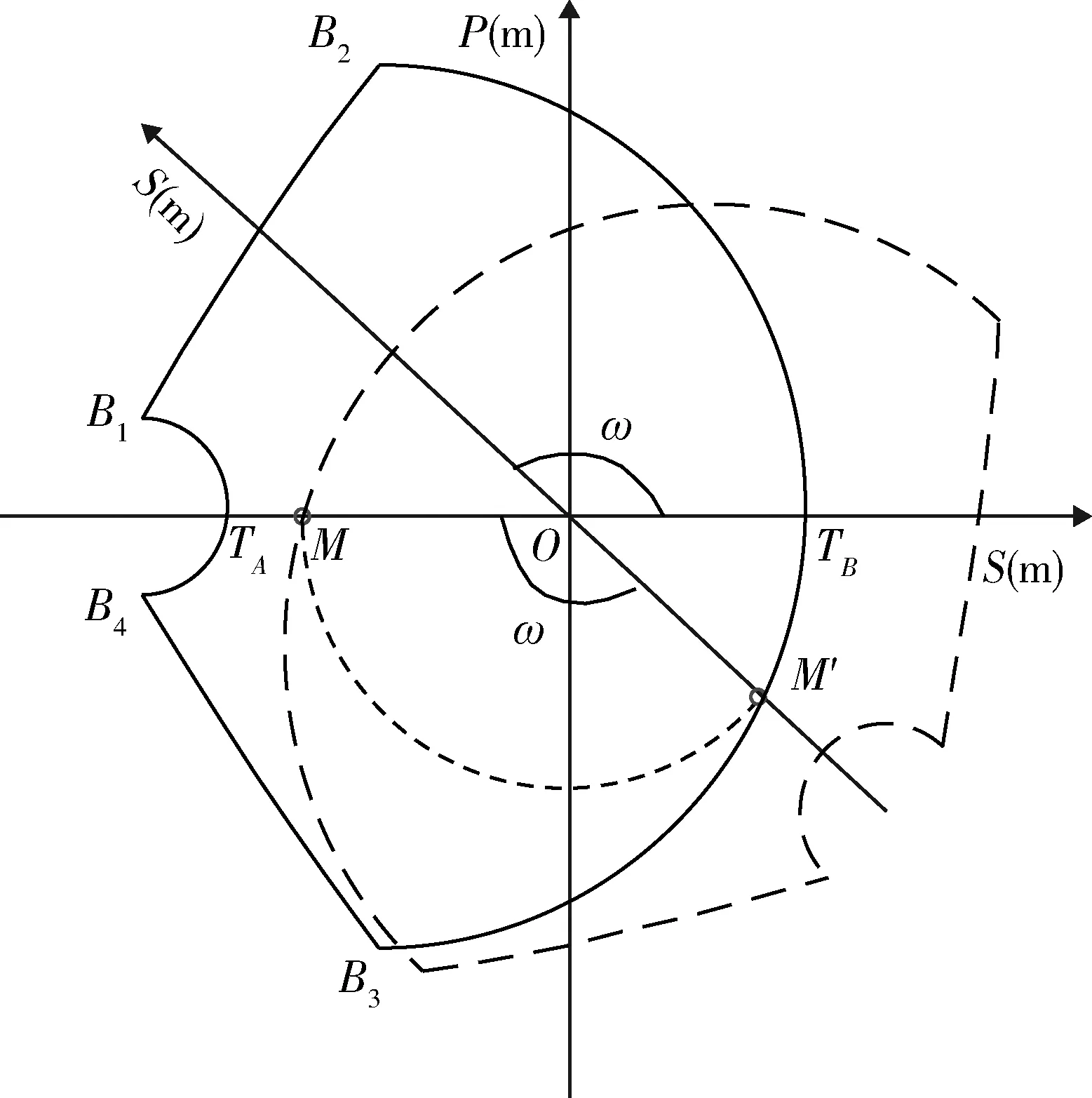
图6 火力单元的防护角Fig.6 Cover angle of the fire unit
由图6中可以分析得到,针对保卫目标点M,火力单元的防护区以火力单元位置点O为圆心逆时针旋转ω,在此期间目标点一直处于火力单元的防护区域内,说明将火力单元部署在O点可以防御在ω角度范围内对目标点造成威胁的来袭弹头。由图中可知旋转火力单元的防护区应对各个方向的来袭目标所形成的防护角,可以用旋转保卫目标位置点来表示。即以O点为圆心,目标到火力单元部署点的距离dOM为半径,顺时针旋转ω,在转动的过程中目标点始终位于火力单元的防护区域内,则说明将火力单元部署在O点可以防御来袭方向为目标点转过角度的对顶角范围内的威胁。用旋转目标点的方法代替旋转火力单元防护区的方式来计算防护角更直观明了。
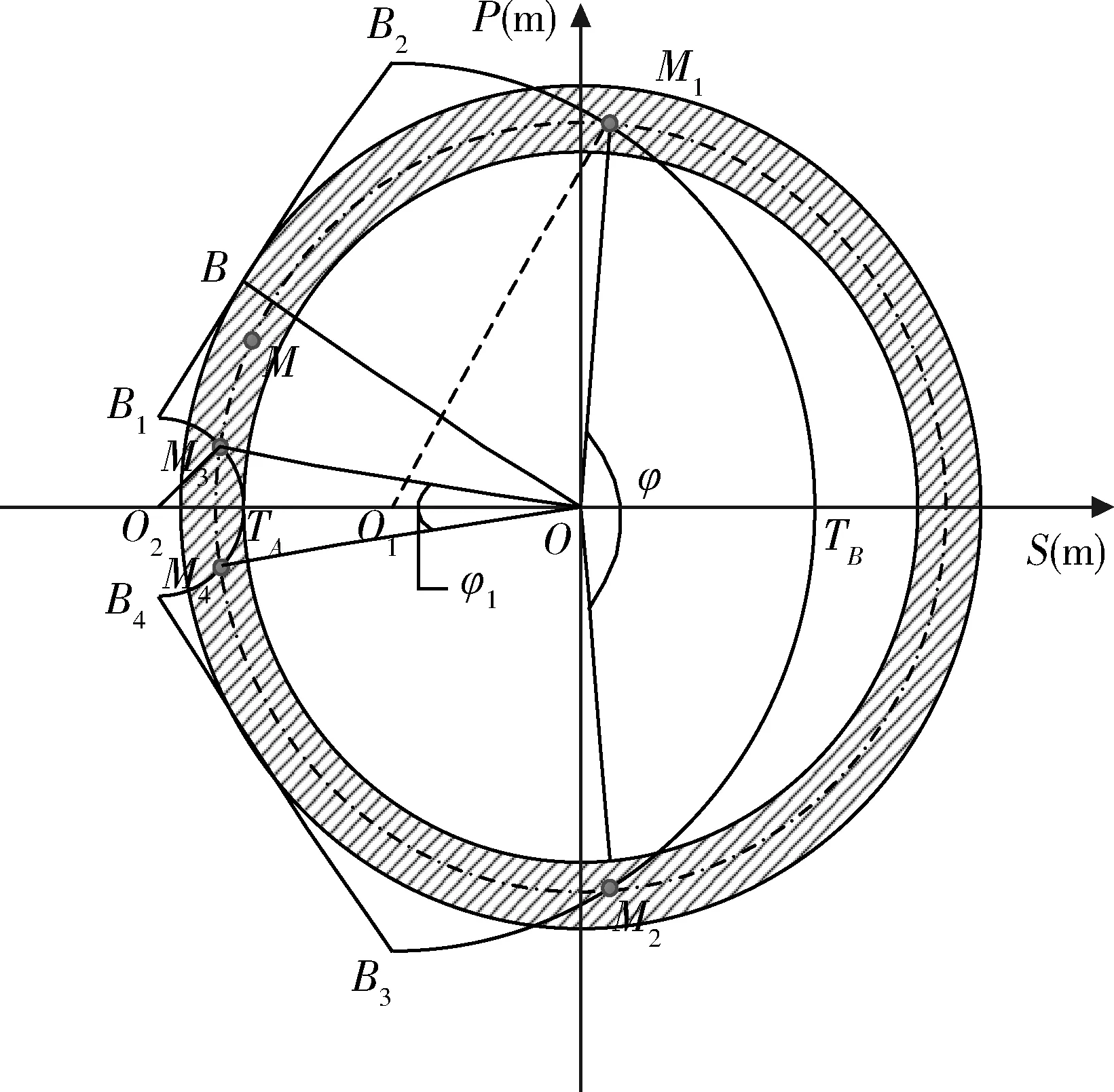
依据防护区的边界条件集B(D,φ),可以用圆环来对防护区进行分解,当保卫目标位于防护区内不同的位置时,火力单元对保卫目标的防护角不同。
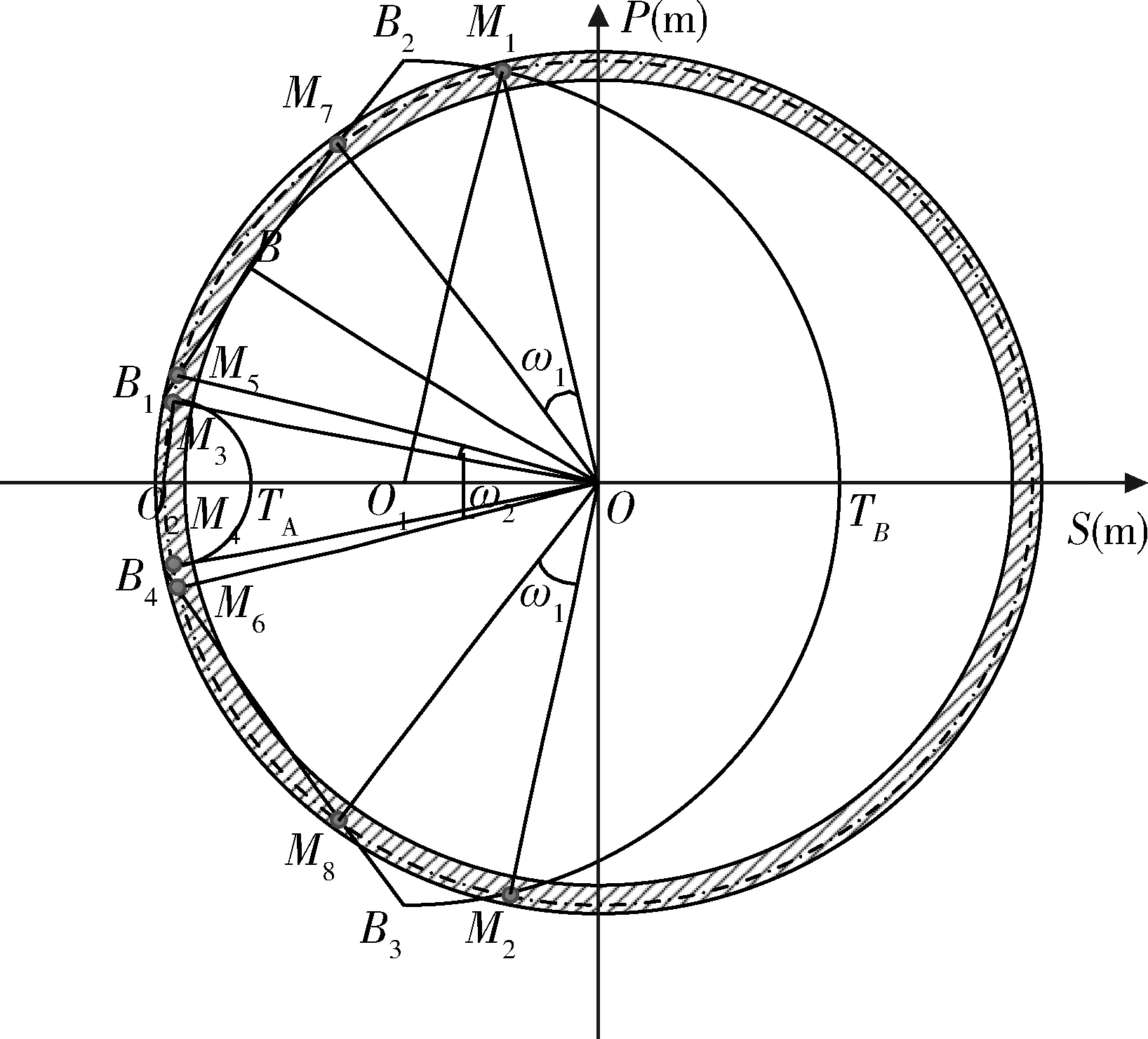
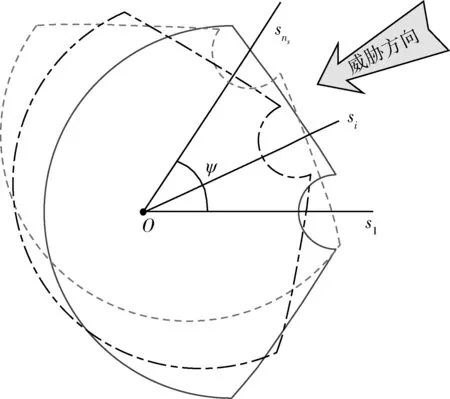
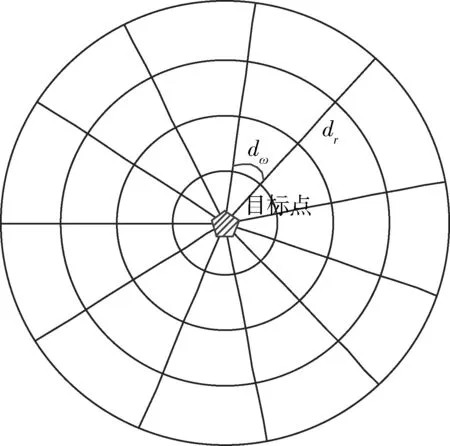
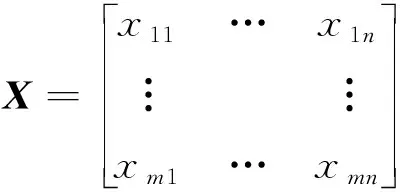
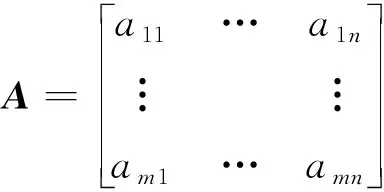
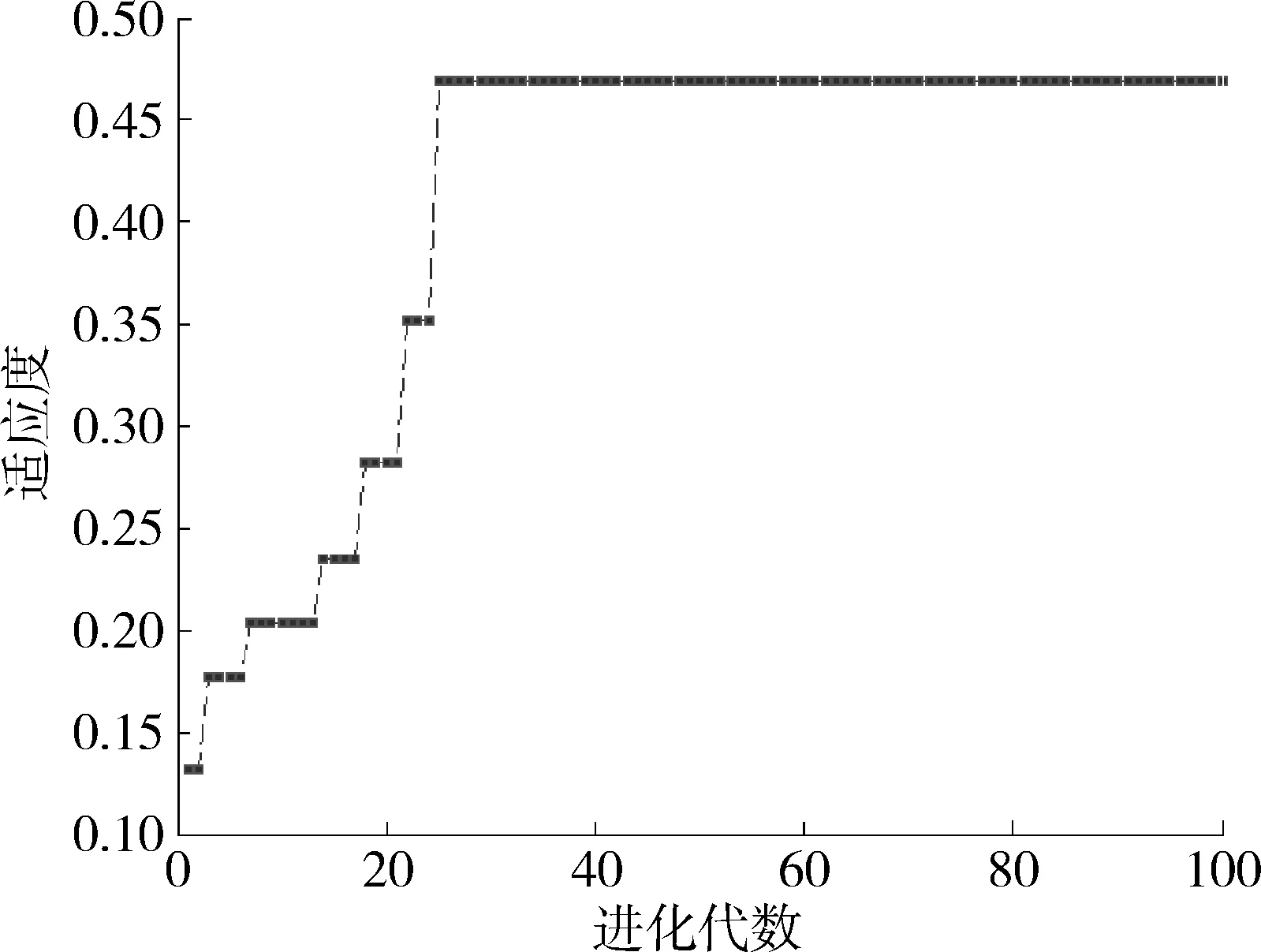
dOM 图7 dOM dOTB (1) 此时防护角ω=360°-φ。 图8 dOTB 图9 dOTA dOTA (2) 此时防护角ω=360-φ-φ1。 dOB 图10 dOB (3) 此时防护角ω=2(ω1+ω2)。 dOB1 图11 dOB1 (4) 此时防护角ω=2ω1。 当dOM>dOB2。保卫目标始终位于火力单元的防护区之外,此时火力单元对保卫目标的防护角为0°。 由阵地对所保卫目标的防护角可知,当阵地部署在所保卫目标点附近时,阵地能够对目标进行全方位的防护,但是由于单个阵地的作战,不能保证同时应对多个攻击的弹道导弹,并且也不能保证对一个来袭弹道导弹进行多次打击,所以在应对扇形方向的威胁时,应该事先分析敌方在一波次中最有可能的进攻方式,以及根据拦截弹的性能,预先制定交战规则,确定对来袭弹道导弹分配几个阵地。 4.2.1 扇形威胁区域的可部署区集合 针对确定的被保卫目标点,针对任何一个方向上都有一个可部署区,对于扇形的威胁方向,可将扇形区域进行等分为ns个方向,则针对扇形威胁的可部署区为ns个方向上的可部署区的集合,如图12所示,所有可部署区外边界包围的区域即为针对扇形威胁的可部署区。 图12 应对扇形威胁的可部署区Fig.12 Deployable area that responds to a sector threat 图12中ψ为威胁方向的角度范围。si为将扇形区域进行划分后的方向,i=2,3,…,ns-1。 对于每个威胁方向上的可部署区内任一点(包含边界上)的坐标(xs,ys),则任一点相对于所保卫目标的角度和距离为[13] (5) (6) 针对每一个方向上的威胁都有一个可部署区域,所以针对扇形区域威胁的可部署区是所有方向上可部署区域的集合,可用极坐标集的形式表示为B(d,φ),以s1方向为极坐标的起始方向。d为可部署区集中在φ方向上的边界,表示为 d=max(d1,d2,…,dn), (7) 式中:n为将扇形威胁方向进行等分的数量;di(i=1,2,…,n)表示针对第i个方向上的可部署区在φ方向上的边界与被保卫目标中心的距离。 4.2.2 部署区域量化 围绕着所保卫目标,对连续的地图进行离散采样[14]。环形区域的半径为拦截弹可部署区的距离目标点的最远边界距离。阵地部署点采用地面极坐标表示为p(ω,r),选取威胁扇形的一条边作为极坐标的0°方向,进行采样时将方向参量ω和距离参量r选取步长dω和dr将连续的地形进行离散化网格处理,武器阵地部署点如下图 13所示。 图13 环形网格Fig.13 Ring grid 武器阵地的部署位置矩阵可以表示为 (8) 矩阵中的行数代表方向位置,列数代表距离位置,式中 (9) 在部署位置矩阵中还可以将地形因素加入,若该地形因素对阵地的影响因素为 (10) (11) 地形因素矩阵中既体现了实际环境对部署的影响,也包含人为的主观偏好因素在内。令tij=xijaij,i=1,2,…,m,j=1,2,…,n则将地形因素考虑在内的综合部署位置矩阵为T=(tij)m×n。地形因素的好坏直接影响到部署的费用和作战效能,在将地形因素加入目标评价函数时,可以转换为成本型指标,即为了达到与理想地形相同的作战效能,必须增加一部分额外的费用。假设在理想地形下部署一个阵地所需费用为E,则将地形因素考虑在内时,部署阵地的成本为 (12) 4.2.3 部署约束条件 (1) 时间约束条件 假设预警系统探测到来袭弹道导弹的目标特性的时刻为t0,预警系统信息处理到传输给拦截弹阵地时间间隔为td1,拦截弹从接受指令到发射的最小反应时间间隔为td2,拦截弹飞行至拦截点的时间为td3。来袭弹道导弹到达理论拦截点的时刻为tl。则在来袭弹道导弹的弹道轨迹上的理论拦截点的应满足: tl≥t0+td1+td2+td3. (13) 针对多个目标或者对一个目标进行多次射击时,同一个阵地相邻两发拦截弹的发射时间间隔为td。 (2) 空间约束条件 空间约束使得部署阵地上的拦截弹能够对某一个或者多个方向上的来袭弹道导弹进行拦截。即存在至少一条来袭弹道导弹的轨迹穿过拦截弹的空间杀伤区。在本模型中转换为使得部署位置点处于可部署区集中。即对于阵地位置点xij: dr×j≤di×dw,i=1,2,…,m,j=1,2,…,n, (14) 式中:di×dw表示在可部署集中,在i×dw角度方向上的边界。 所有阵地对目标点的防护角度应不小于威胁的扇形角度范围。保证在敌方威胁方向上火力能够紧密衔接,防止来袭弹道导弹在防御空隙中逃脱。即: (15) 式中:ψij表示部署在第i个方位步长上,第j个距离步长位置上的阵地对目标点的防护角。 假设对于一个来袭目标只采用1发导弹对其进行拦截。在扇形区域内应该能保证最少能同时发射nz枚拦截弹,来保证最少能够同时应对nz枚来袭弹道导弹的攻击。但是导弹的进攻方向不确定所以应该保证在可能威胁的方向上有nz重防护,则阵地数目应该满足: (16) 相邻2个火力单元之间为了避免电磁干扰,最小距离要求不小于dz。∀xij=1,xqt=1,满足: (17) 4.2.4 目标函数 在进行方案的优选时,需要将每个方案在属性集下的评估价值进行综合考虑。属性集是反映部署方案指标的集合,对应于方案在属性指标下的效能值。由于各个属性指标之间存在着差异,首先需要对不同的指标进行规范化处理,将指标分为成本型和效益型指标,在进行方案的选择时,要求成本型指标越小越好,效益型指标越大越好。 针对本文中的目标属性为期望阵地个数最少,防护角重叠最大,综合拦截效能最大以火力单元相互之间的防护能力。假设任意部署方案X在这t个目标属性下的指标分别为y1,y2,…,yt。 对于成本型指标的规范化处理: (18) 对于效益型指标的规范化处理: (19) 式中:ymin表示所有可能的方案中,在第i个目标属性下的最小指标值;ymax表示所有可能的方案中,在第i个目标属性下的最大指标值[15]。 (20) 权重体现了对不同目标属性的重要程度的分配,不同的权重分配会导致优选出的方案不同。权重的确定可以根据决策者的对不同目标属性的评价来分配权重。 基于遗传算法的火力单元优化部署的步骤为: (1) 编码 针对该模型的变量,部署位置在以落点为原点的坐标系中,在环形网格区域内的每个网格交点作为一个变量,变量的取值只有0和1。当变量取0时,表示在该位置没有部署阵地,当变量取1时表示变量在该位置部署阵地。考虑到变量的取值情况,在进行编码的时候选用二进制编码的形式,这样既符合计算机处理信息的原理,也方便对染色体进行遗传、变异等操作。对环形区域进行网格划分,将其划分为m个方向,每个方向上划分为n个点,则一共有m×n个位置,所以有m×n个变量,使用长度为m×n的二进制编码表示参数变量,则共有2m×n种不同形式的编码。变量代表的位置与参数编码的关系为:第i个方向,第j个距离步长位置上对应的染色体的位置为i×m+j。 (2) 产生初始种群 设定每一代种群个体的数量为M,按照步骤1中的编码方式随机生成M个个体。 在扇形区域内应该能保证最少能同时发射nz枚拦截弹,考虑到同一阵地发射时间的限制,所以拦截阵地至少要部署nz个,所以在每次生成初始个体时应该确保至少有nz个位置上的染色体编码为1。 (3) 适应度值选取 首先将每个染色体进行解码,即将染色体变量值转换为位置变量值,即 (21) 式中:k代表每条染色体中第k个位置;xk为每条染色体中第k个位置的编码值;floor表示取整;rem表示取余;xij表示第i个方向步长,第j个距离步长位置上的变量。 评价目标函数为f(X),本文是求极大值问题,将目标函数值转换为适应度。 eval(UK)=f(XK),K=1,2,…,M. (22) (4) 选择 通过用计算机的轮盘方式增加popsize为种群个数,依据个体的适应度值所占的总的适应度值的百分比区间进行选择。每一代种群适应度值总和 (23) 第K个染色体被复制的累积概率为 (24) 则第K个染色体的适应度区间为[QK-1,QK]。 适应度值越大,其区间跨度越大,轮盘转入其区间的概率就越大。每旋转一次就会选中一个个体,通过进行M次选择,形成新一代的种群。 (5) 交叉 交叉使得新个体能够实现信息的交换和保持父辈的特征。每次交叉随机选中种群中的2个个体,并随机选择个体染色体交叉的位置,根据设定的交叉概率,进行交换时产生的随机数小于交叉概率则进行交换,否则不进行交换。 (6) 变异 每次随机选中一个个体,并随即选择其变异位置,进行变异时如果产生的随机数小于变异概率则将选中的染色体的位置编码进行翻转,即编码为1的变为0,编码为0的变为1,如果变异时产生的随机数大于变异概率则不进行变异。 (7) 染色体可行性判断 在生成初始种群后和每一代的选择,交叉,变异的进化之后,要对每个个体进行判断是否满足各种约束条件。在对新的种群按照步骤3中的算法进行解码之后,代入式(16) 判断在每个方向上是否满足最小覆盖重数,代入式(17) 判断每个阵地之间的距离是否满足最小距离要求。如果全部满足约束条件则依次按照步骤进行。若不满足约束条件则重新进行筛选,直到选出满足要求的个体。 (8) 终止 当进化到设定的进化代数时,终止运算。 假设威胁方向的扇形角度为90°,在一波次的攻击中最多不超过3枚导弹,导弹的进攻方向为扇形威胁方向内的某个不确定方向。进攻导弹的型号以及拦截弹的型号选择上文中的导弹模型参数。权重矢量选为wA=(0.6,0.1,0.2,0.1)。环形网格的方位角度步长取10°,半径步长为10 km,相邻2个阵地的最小距离为50 km。地形影响因素用m×n的随机数矩阵在程序中生成。由图3可知拦截弹的拦截高度范围在450 km以内,,对于5 000 km射程左右的弹道导弹,将拦截弹在靠近目标侧的下降段范围拦截,始终满足式(13)的时间约束条件。 遗传算法中初始种群为300个,进化次数为100代。适应度曲线如图14所示。 图14 适应度函数进化曲线Fig.14 Fitness function evolution curve 由图14中可以看出,当进化到25代时适应度值不再变化,已筛选出最优部署位置为3个位置如图15所示。图15中三角点所在位置为阵地部署点,坐标点为坐标分别为(70°,160),(60°,110),(0°,100)。此时对扇形威胁区域内的每个方向上的最少覆盖次数为3次,这3个阵地对划分的每个方向上的拦截纵深长度总和为:1 095.1 km。将阵地位置代入式(17)和式(1)~(4)中得到阵地之间的相互防护角均为360° 并且阵地1,2和3相互之间的距离分别为:55,157,105 km全部满足阵地之间的最小距离约束。 图15 阵地部署位置Fig.15 Front deployment position 本文针对重点资产防御中反导武器的部署问题,建立了拦截弹的防护区,部署区和防护角模型,针对不同作战场景下的威胁,建立了优化部署模型。该模型对中段反导作战有一定的理论指导意义。 该仿真结果表明部署的优化选择与参考的目标价值的选取相关,对于属性集中各属性指标权重的分配的不同会对部署的结果造成影响,在实际部署中应该综合各项指标并分配合适的权重,才能更好的适应实际作战的需要。
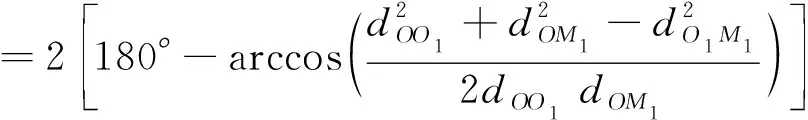
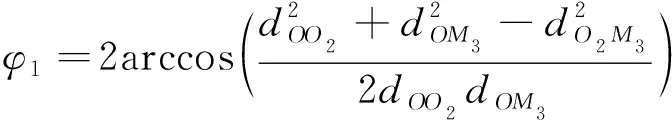
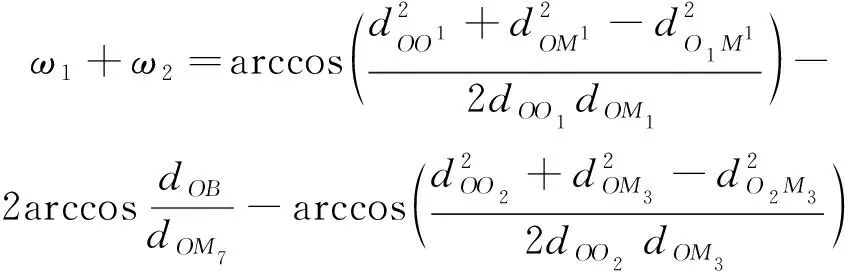
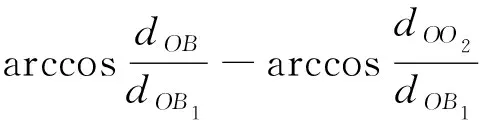
4.2 扇形威胁的阵地部署模型
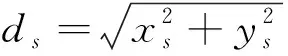
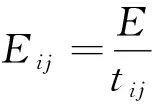
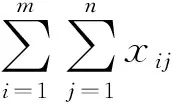
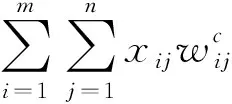
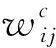
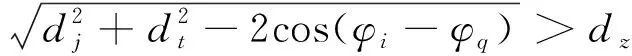
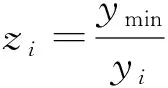
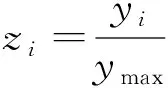
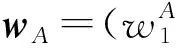
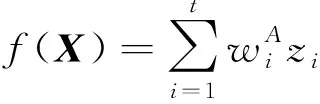
4.3 基于遗传算法的阵地部署优化求解
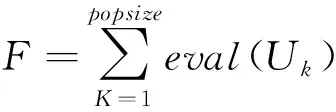
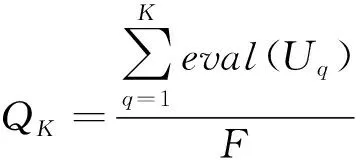
4.4 扇形威胁阵地部署仿真分析
5 结束语
