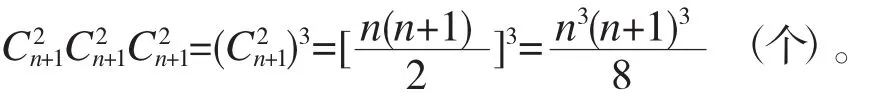一道组合计数问题的推广

曹博瑞，刘 铁

（安康学院 数学与统计学院，陕西 安康 725000）

在《竞赛数学教程》一书中有这样一道组合计数题：“在m×n(m≤n)的方格中，有多少个平行于网格线的长方形和正方形？”[1]，此题表述简单，但内涵丰富，以一个简单的几何计数问题为载体，重点考察学生的归纳推理、分类讨论、数形结合的能力，以及由特殊到一般的思想方法，凸显了对学生创造性思维能力考查。所谓计数问题，就是要计算给定的有限集合的元素个数，此类问题不仅是日常生活中经常遇到的问题，也是数学竞赛中常见的一类问题，还是组合数学各个模块的重要基础。目前人们已经总结出许多计数的方法和技巧，如枚举法、映射法、递推法等，书中此题就用到了映射法，但过程过于简略，不利于学生理解。本文对此问题给出了详细的求解过程，并将问题推广到空间中，且予以详尽解答，得到了相应的结论。

1 计数方法：映射法

当我们遇到组合计数问题时，如果直接计算集合A中的元素个数较困难，则可设法建立一个从集合A到集合B的双射f，并且集合B中的元素个数容易算出，那么所求集合A中的元素个数为，这种计数方法称为映射法（或配对原理）。

2 问题与求解

问题1在m×n(m≤n)的方格中（如图1为5×7的方格），有多少个平行于网格线的长方形和正方形？

图1 5×7的方格

解（1） 求长方形个数。

在m×n(m≤n)的方格中，有m+1条横边，n+1条竖边。因为正方形是特殊的长方形，所以正方形也是长方形。长方形有4条边，每个长方形的两条横边可以从m+1条横边中任意选取，有C2m+1种取法，两条竖边可以从n+1条竖边中任意选取，有C2n+1种取法，这种取法是一一对应的。故长方形的个数为

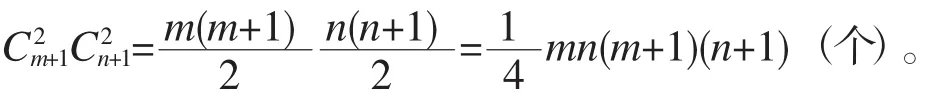
（2）求正方形个数。

当正方形的边长为1时，让横（竖）边的第1条作为它其中的一条横（竖）边，则只能取第2条横（竖）边作为其对边，以此类推，让横（竖）边第2，3，…，m-1（或n-1），m（或n） 条作为正方形其中一条横（竖） 边，则只能取第3，4，…，m（或n），m+1（或n+1） 条横（竖） 边作为其对边。所以，其横、竖边各有(m+1-1)=m、(n+1-1)=n种取法，利用乘法原理，则边长为1的正方形有(m+1-1)(n+1-1)=mn个。

同理，当正方形的边长为2，3，…，m-1，m时（因为在m×n的方格中，m≤n，所以构成的正方形的最大边长只能取到m），对应边长的正方形分 别 有 (m+1-2)(n+1-2)， (m+1-3)(n+1-3)， … ，[m+1-(m-1)][n+1-(m-1)]，(m+1-m)(n+1-m)个。

所以，所求方格中含有边长为k的正方形个数一一对应于其中相距为k个小方格的两条横边和两条竖边的选取方法，故所求方格中含有的正方形个数为

特别地，当m=n时，其长方形个数为

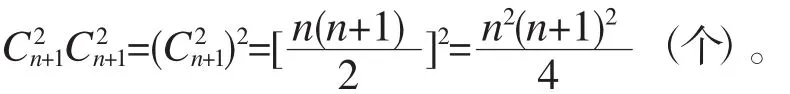
其正方形个数为

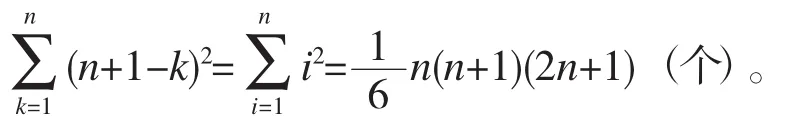
3 问题推广

此问题如果推广到空间上，情况又如何呢？即有

问题2由m×n×k(m≤n≤k)个小正方体组成的空间立体中（如图2为5×5×6的空间立体），有多少个平行于网格面的长方体和正方体？

图2 5×5×6的空间立体

解求长方体和正方体的个数与求长方形和正方形的个数的方法类似。

（1）求长方体个数。

在由m×n×k(m≤n≤k)个小正方体组成的空间立体中，有m+1个横面，n+1个纵面及k+1个水平面。因为正方体是特殊的长方体，所以正方体也是长方体。长方体有6个面，每个长方体的两个横面可以从m+1个横面中任意选取，有种取法，两个纵面可以从n+1个纵面中任意选取，有种取法，两个水平面可以从k+1个水平面中任意选取，有种取法，这种取法是一一对应的。故长方体的个数为

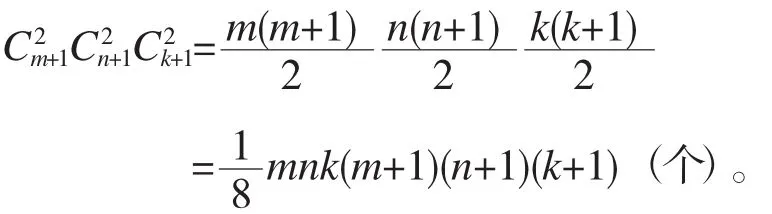
（2）求正方体个数。

当正方体的棱长为1时，让横（纵、水平）面的第1个面作为它其中的一个横（纵、水平）面，则只能取第2个横（纵、水平）面作为其对面，以此类推，让横（纵、水平） 面第2，3，…，m-1（或n-1，k-1），m（或n，k） 个面作为正方体的一个横（纵、水平）面，则只能取第3，4，…，m（或n，k），m+1（或n+1，k+1） 个横（纵、水平）面作为其对面。所以，其横、纵、水平面各有(m+1-1)=m、(n+1-1)=n、(k+1-1)=k种取法，利用乘法原理，则棱长为1的正方体有(m+1-1)(n+1-1)(k+1-1)=mnk个。

同理，当正方体棱长为2，3，…，m-1，m时（因在m×n×k正方体组成的空间立体中，m≤n≤k，所以要构成正方体其最大棱长只能取到m），对应棱长的正方体分别有(m+1-2)(n+1-2)(k+1-2)，(m+1-3)(n+1-3)(k+1-3)，…，[m+1-(m-1)][n+1-(m-1)][k+1-(m-1)]，(m+1-m)(n+1-m)(k+1-m)个。

所以，所求空间立体中含有棱长为i的正方体个数一一对应于其中相距为i个面的两个横（纵、水平）面的选取方法，故所求空间立体中含有的正方体个数为

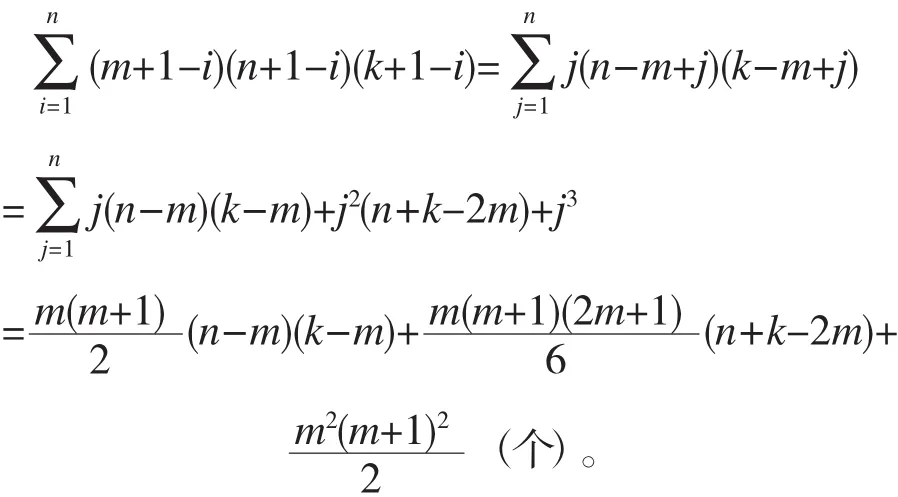
特别地，当n=m=k时，其长方体个数为其正方体个数为