Theoretical calculation of equilibrium Mg isotope fractionation between silicate melt and its vapor

···

Abstract Isotope fractionation during the evaporation of silicate melt and condensation of vapor has been widely used to explain various isotope signals observed in lunar soils,cosmic spherules,calcium–aluminum-rich inclusions,and bulk compositions of planetary materials.During evaporation and condensation,the equilibrium isotope fractionation factor(α)between high-temperature silicate melt and vapor is a fundamental parameter that can constrain the melt’s isotopic compositions.However,equilibrium α is difficult to calibrate experimentally.Here we used Mg as an example and calculated equilibrium Mg isotope fractionation in MgSiO3and Mg2SiO4melt–vapor systems based on first-principles molecular dynamics and the hightemperature approximation of the Bigeleisen–Mayer equation.We found that,at 2500 K,δ25Mg values in the MgSiO3and Mg2SiO4melts were 0.141±0.004 and 0.143±0.003‰ more positive than in their respective vapors. The corresponding δ26Mg values were 0.270±0.008 and 0.274±0.006‰more positive than in vapors, respectively. The general α-T equations describing the equilibrium Mg α in MgSiO3and Mg2SiO4 melt–vapor systems were: andrespectively,where m is the mass of light isotope24Mg and m′is the mass of the heavier isotope,25Mg or26Mg.These results offer a necessary parameter for mechanistic understanding of Mg isotope fractionation during evaporation and condensation that commonly occurs during the early stages of planetary formation and evolution.

Keywords Equilibrium Mg isotope fractionation⋅Force constant⋅Structural optimization ⋅RPFR

1 Introduction

Evaporation and condensation are two of the most common events that occur during the evolution of planetary materials because,according to the nebular hypothesis,all of the materials started as a cloud of molecular vapor and dust,followed by coagulation,impact,and thermal events.Materials evaporate and condense during these processes.

Several possible explanations have been proposed to account for the discrepancy,including diffusion in the melt,sample size,evaporating species,evaporation coefficient of isotopes,recondensation,and the equilibrium isotope fractionation factor(α).The first three possible causes have been excluded by corresponding experiments and thermodynamic calculations (Richter et al.2002,2007),while the last three factors are not well investigated.Among them,equilibrium isotope fractionation is a parameter determined by the ratio of the rate constant of evaporation to that of condensation.Currently,few experiments have been conducted to calibrate equilibrium isotope fractionation between melt and vapor.Two experiments,in which vapor was supposed to be in equilibrium with melt,were done by Richter et al.(2002).They found an equilibrium Mgbetween CaO–MgO–Al2O3–SiO2(CMAS) melt and vapor at 1400°C of 0.99989 ± 0.00060（2σ）.This calibrated value allows that the fractionation factor could be greater or less than 1.000.

One of the difficulties in getting an accurate experimental result is the design of evaporation experiments at high temperatures,e.g.,＞ 2000 °C Although α at high temperatures is expected to be small,it should not be ignored.Hin et al.(2017)reported that Earth and differentiated planetary bodies are enriched in25Mg by 0.02‰compared to primitive chondrites,and suggested that equilibrium Mg isotope fractionation between melt and vapor over 2500 K is responsible.This is because predicted potassium isotope fractionation constrained by kinetic Mg isotope fractionation is inconsistent with observed potassium isotope fractionation.In their computation of equilibrium αMg（l）-Mg（g）,the reduced partition function(β)value(Schauble 2011)is based on crystal structure even though crystal structure may not be a good approximation for melt structure when calculating β values,especially at high temperatures.

Equilibrium α between melt and vapor has not been theoretically calculated for Mg or for any other element.Considering that the structure and bond environment of the melt are different from those of the vapor in which an element resides,we expect a small but observable equilibrium isotope fractionation at high temperatures.In this paper,we used Mg as an example to calculate equilibrium isotope fractionation in MgSiO3and Mg2SiO4melt–vapor systems based on first-principles molecular dynamics(FPMD)and high-temperature approximation of the Bigeleisen–Mayer equation.This is a necessary step to understanding evaporation and condensation processes during planetary formation and evolution.

2 Methodology

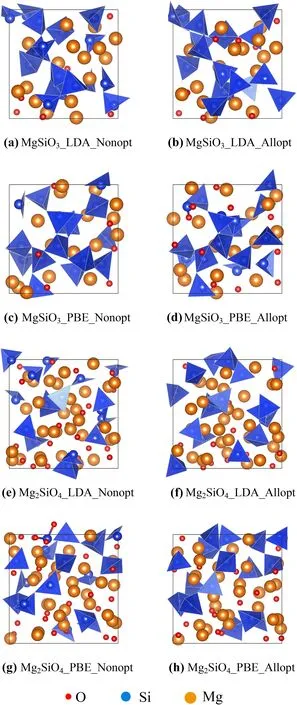
Simulating the structure of MgSiO3and Mg2SiO4melts based on FPMD has proven viable(Stixrude and Karki 2005;de Koker et al.2008).We first used the Vienna Ab initio Simulation Package(VASP)code(Kresse and Furthmüller 1996)to perform FPMD simulations of the MgSiO3and Mg2SiO4melts within the local density approximation(LDA)(Kresse and Hafner 1994)and the generalized gradient approximation(GGA)(Kresse and Joubert 1999).Both ultra-soft pseudopotentials in LDA and the projector-augmented wave method in GGA were used with a cutoff energy of 400 eV and gamma point sampling.A canonical ensemble(e.g.NVT)with periodic boundary conditions was used in the simulation.Our cubic supercells of MgSiO3and Mg2SiO4contained 80 atoms(16 formula units)and 112 atoms(16 formula units),respectively.The corresponding volumes were 38.9 and 52.36 cm3/mol.The initial structure was melted at 6000 K and then isochorically quenched to 4000 and 2500 K.We ran FPMD simulation at each temperature for 3 ps.After obtaining the steady structure of the MgSiO3and Mg2SiO4melts at 2500 K,we captured snapshots at ionic steps=2100,2200,2300,2400,2500,2600,2700,2800,2900,and 3000.Then,we calculated force constants for each Mg atom in the ten con figurations in three situations:all-atom optimization,single-atom optimization,and non-optimization.All-atom optimization means structure optimization is performed for all atoms in the cell,while only the structure of the single atom of interest is optimized in single-atom optimization.Non-optimization means that no structure optimization is conducted.Force convergence criteria EDIFFG in structure optimization is equal to-0.001.A cutoff energy of 600 eV is used in structure optimization and calculating force constants with EDIFF=10E-8.The average values of force constants for all Mg atoms in the ten con figurations were taken as the approximate force constant for Mg in the melt.Then,we used a high-temperature approximation of the Bigeleisen–Mayer equation(Bigeleisen and Mayer 1947;Wolfsberg et al.2010)to calculate the reduced partition function ratio(RPFR)of Mg in the melt:

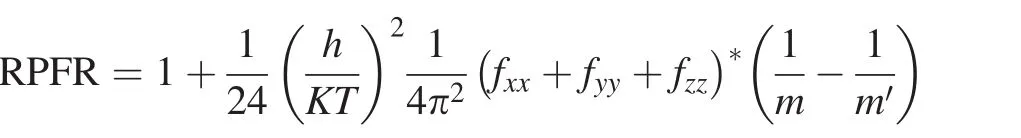
◂Fig.1 a MgSiO3_LDA is the snapshot of the MgSiO3melt at the 2100th step in FPMD within LDA at 2500 K;b MgSiO3_LDA_Allopt is the all-atom optimized structure of(a);c MgSiO3_PBE is the snapshot of the MgSiO3melt at the 2100th step in FPMD within Perdew–Burke–Ernzerhof(PBE)at 2500 K;d MgSiO3_PBE_Allopt is the all-atom optimized structure of(c);e Mg2SiO4_LDA is the snapshot of the Mg2SiO4melt at the 2100th step in FPMD within LDA at 2500 K;f Mg2SiO4_LDA_Allopt is the all-atom optimized structure of(e);g Mg2SiO4_PBE is the snapshot of the Mg2SiO4melt at the 2100th step in FPMD within PBE at 2500 K;h Mg2SiO4_PBE_Allopt is the all-atom optimized structure of(g)

where fxx,fyy,and fzzare the diagonal elements of the force constant matrix;m the mass of the light isotope;m′the mass of the heavier isotope;T temperature;K the Boltzmann constant;and h Planck’s constant.

To calculate equilibrium Mg isotope fractionation between melt and vapor,we also needed the RPFR of Mg in the vapor.One key factor in determining the RPFR of Mg in vapor is the gaseous species of Mg.It has been determined by both experiments and thermodynamic calculations that the dominant gaseous species of Mg over silicate melt is Mg atoms,whose concentration is at least two orders of magnitude higher than the secondary gaseous species,MgO(Richter et al.2002,2007).Mg in vapor can be regarded as atomic Mg in form and its RPFR should be 1 given negligible intermolecular bonding in gas.Therefore,the equilibrium

3 Results

3.1 Structural optimization

We performed all-atom structural optimization based on the extracted con figurations to check whether we could obtain metastable structures of the MgSiO3and Mg2SiO4melts that represent ideal structures of the melts.As shown in Fig.1,we used the con figuration at ionic step=2100 as an example and found that all-atom optimized structures maintained the same structural features as non-optimized con figurations.One difference was that more silicon–oxygen tetrahedrons were observed in the all-atom optimized structures.

We also analyzed the Si–O and Mg–O radial distribution function(RDF)for the all-atom optimized structure and non-optimized structure of the 2100th con figuration.The Si–O and Mg–O RDFs of the melt within the last 1 ps were used as references.As shown in Fig.2,the basic shape of the RDFs looks similar,but the first peak for the all-atom optimized structure is much higher than for the non-optimized structure.

3.2 Force constants

We calculated force constants for all Mg atoms in the ten con figurations we extracted.Therefore,for MgSiO3and Mg2SiO4melts,force constants for 160 and 320 Mg atoms were calculated,respectively.Then,we took the average of the force constants under each condition and computed the corresponding standard errors(Table 1).

As shown,both the force constants and their corresponding standard errors in LDA were smaller than in PBE.Force constants were consistently larger and their corresponding standard errors smaller under all-atom optimization than under single-atom optimization.In addition,the force constant of the Mg2SiO4melt was larger than that of the MgSiO3melt under single-atom optimization,but the opposite was the case under all-atom optimization.

3.3 RPFR and fractionation factor

We used the above force constants （fxx+fyy+fzz）to calculate the RPFR value of Mg atoms in the MgSiO3and Mg2SiO4melts.Table 2 shows the computed results of 1000lnα25Mg-24Mg(‰)and 1000lnα26Mg-24Mg(‰)and their corresponding standard errors at 2500 K.

A plot of 1000lnαMg(l)-Mg(g)versus 108/T2is shown in Fig.3.

As we can see,equilibrium Mg isotope fractionation in LDA was smaller than in PBE.Meanwhile,equilibrium Mg isotope fractionation was consistently larger under all-atom optimization than under single-atom optimization.

4 Discussion

Structural comparison and RDF analysis con firmed that ideal metastable structures of the MgSiO3and Mg2SiO4melts were obtained after all-atom optimization.More silicon–oxygen tetrahedrons were expected in all-atom optimized structures than in non-optimized structures because atoms in the all-atom optimized structure were in equilibrium positions and distributed more symmetrically.This also explains why RDF for all-atom optimized structures had a much higher peak.

We report two sets of data here.One is based on LDA using ultrasoft pseudopotentials(USPP),the other on GGA using PBE.LDA tends to underestimate computed properties,while GGA tends to overestimate these properties.Here both isotope fractionation factors and their corresponding standard error in LDA were much smaller than in PBE.The results based on LDA are recommended because FPMD of elasticity,pressure,and volume of silicates has been based on LDA and the results match well with experimental data(Karki 2010).Future experimental data can help validate this recommendation.

The question of which of the three different optimization conditions—non-optimization,single-atom optimization,and all-atom optimization—gives a more accurate equilibrium Mg isotope fractionation factor is determined by a balance between inaccuracy of computation and the deviation from real structures.Although the con figurations under the non-optimization condition represented the real structures of a melt,force constants calculated under nonoptimized structure were not as credible.The inaccuracy of the computation itself was caused by a failure of harmonic approximation since almost all Mg atoms in the non-optimization situation were not in their equilibrium positions.When the computed force constants for part of the Mg atoms are overlarge,the outcome is an erroneously large isotope fractionation for the non-optimized force constant of the Mg2SiO4melt in PBE.For the metastable structures that we obtained under all-atom optimization,computational inaccuracy was minimized,but the ideal structures may have deviated far from the real melt.The differences in isotope fractionation and the corresponding standard error between all-atom optimization and single-atom optimization were predictable because all-atom optimized structures tend to reach global equilibrium,while singleatom optimization will only reach local equilibrium.Single-atom optimization does not change the position of Si and O atoms around Mg atoms,which means that they inherit part of the non-equilibrium information from the initial snapshot.Thus,it is reasonable to conclude that single-atom optimization closely approximates the real structures and minimizes the computational inaccuracy given those structures.

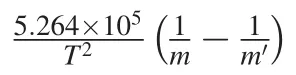
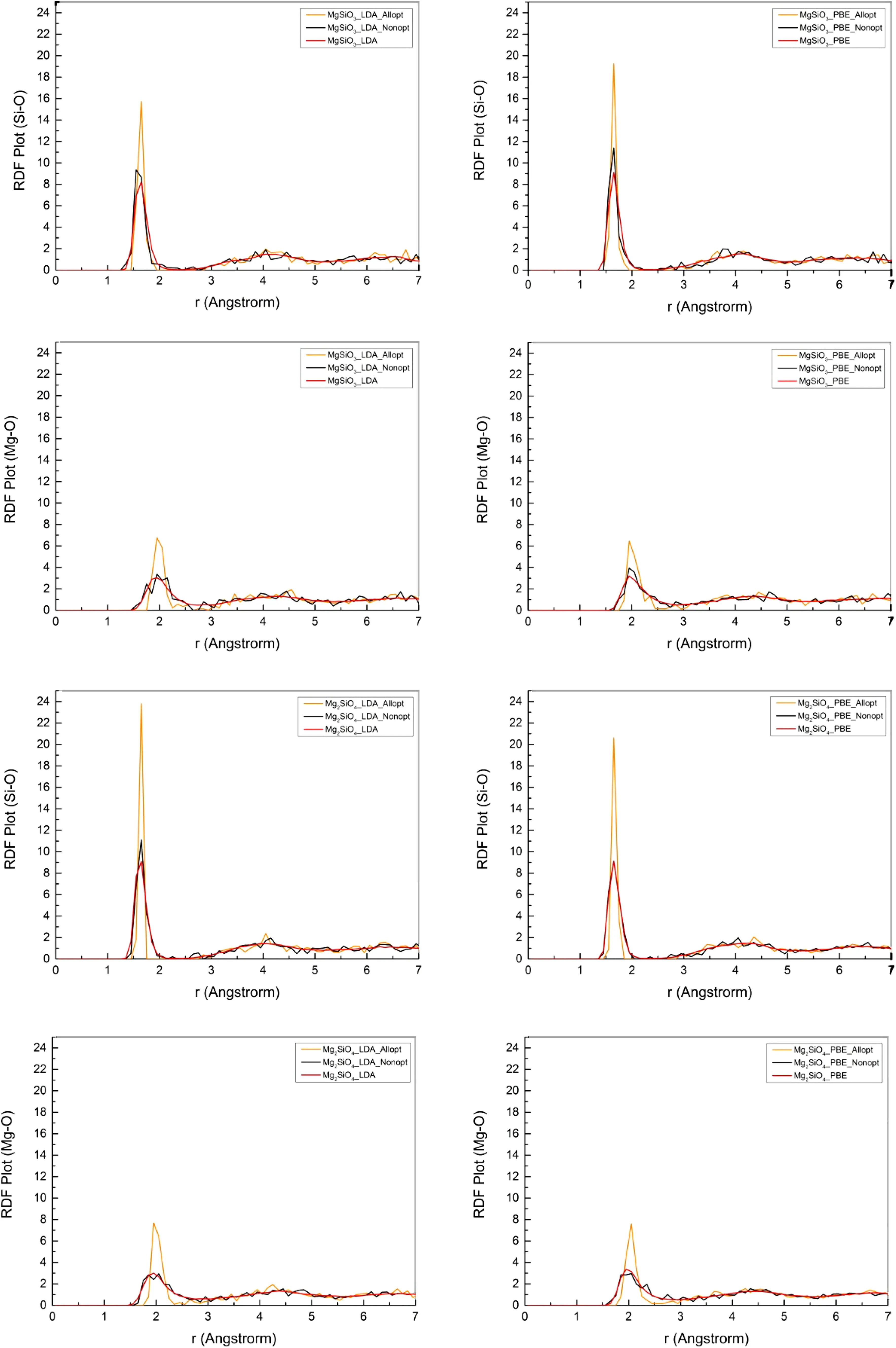
Fig.2 RDFs for MgSiO3and Mg2SiO4melts at 2500 K within the last 1 ps(red line),RDFs for the non-optimized structure of the 2100th con figuration(black line),and RDFs for the all-atom optimized structure of the 2100th con figuration(orange)

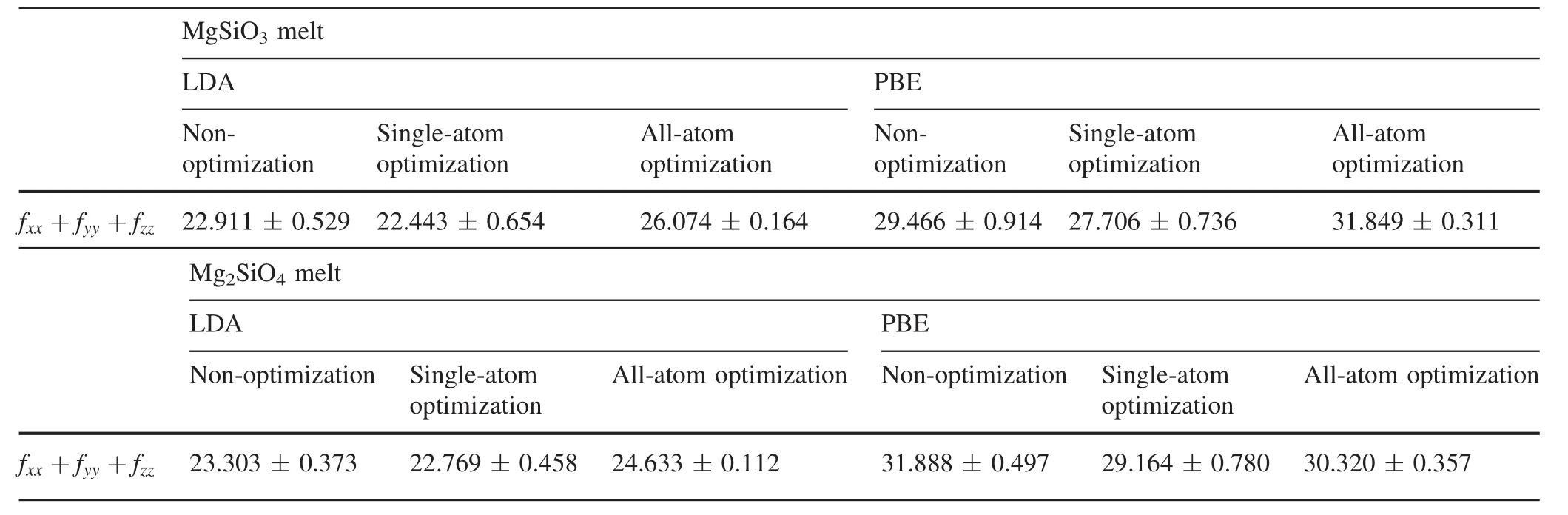
Table 1 Computed force constants under different conditions

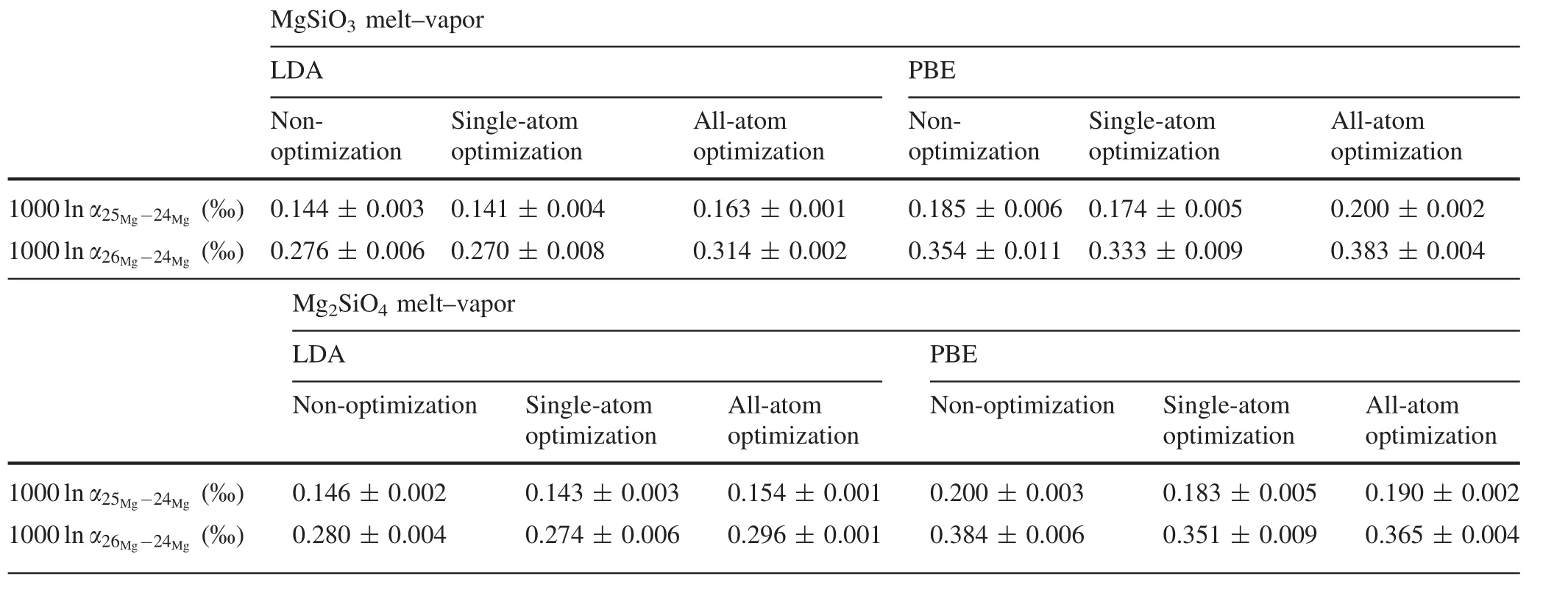
Table 2 Computed 1000lnα25Mg-24Mg(‰)and 1000lnα26Mg-24Mg(‰)at 2500 K

5 Conclusions

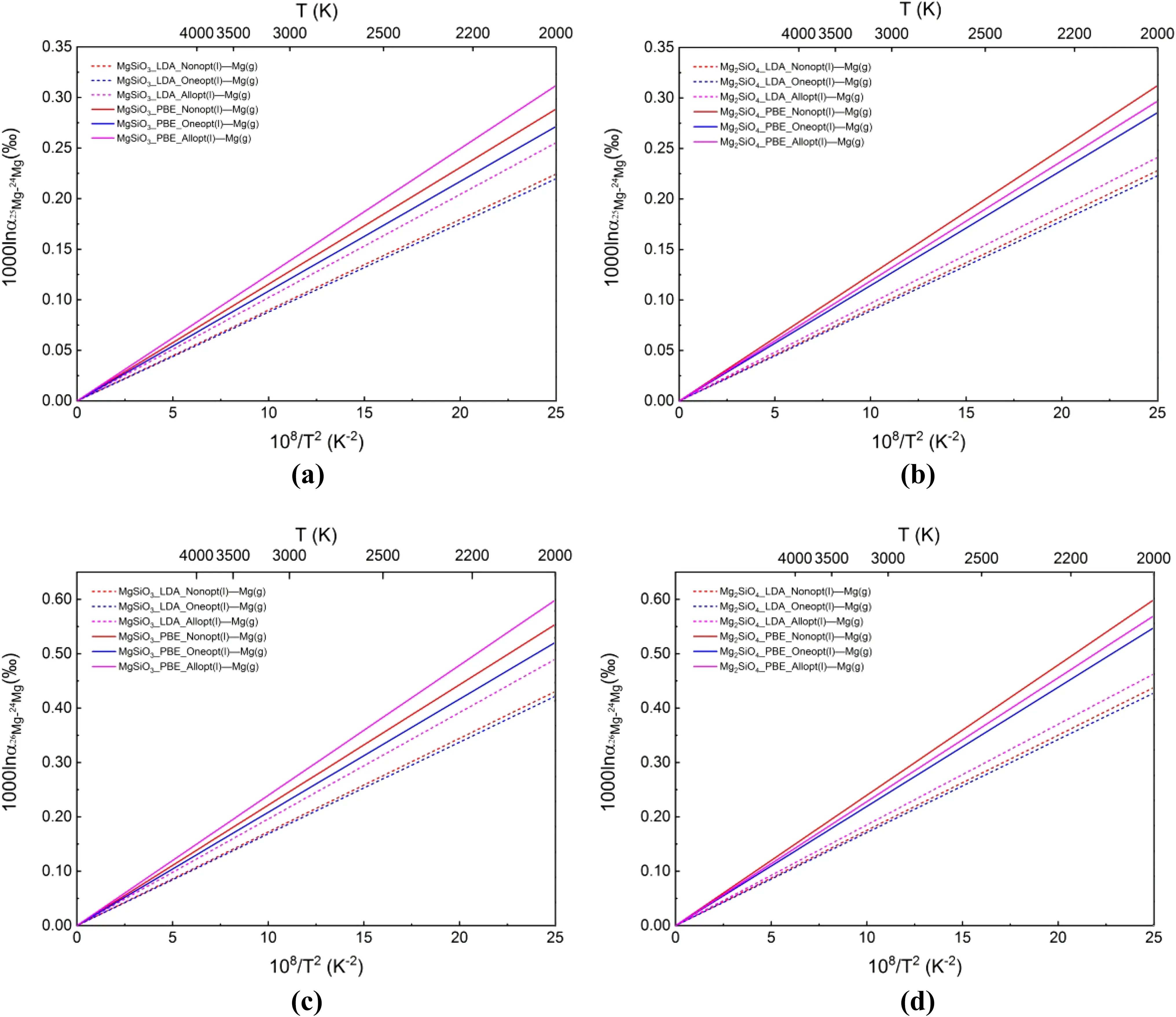
Fig.3 a Computed 1000lnversus 108/T2between the MgSiO3melt and gaseous Mg atoms;b computed 1000lnα25Mg-24Mgversus 108/T2between the Mg2SiO4melt and gaseous Mg atoms;c computed 1000lnα26Mg-24Mgversus 108/T2between the MgSiO3melt and gaseous Mg atoms;d computed 1000lnα26Mg-24Mgversus 108/T2between the Mg2SiO4melt and gaseous Mg atoms

By performing FPMD,calculating force constants based on VASP,and applying the high-temperature approximation of the Bigeleisen–Mayer equation,we obtained equilibrium Mg isotope fractionation between melt and vapor.To get a reliable result,we examined two approximate functions based on electron density—LDA and GGA;and three structural optimization methods.Equilibrium Mg isotope fractionation based on single-atom optimized structure and LDA was the most reliable.In addition,values based on all-atom optimized structure represent the upper limit of equilibrium Mg isotope fractionation.Our simulation focused on the structure of MgSiO3and Mg2SiO4melts only.Multicomponent melts will need more complex computation schemes and are necessary for real-world materials.

AcknowledgementsFinancial support for this work is provided by the strategic priority research program(B)of CAS(XDB18010104)and China NSFC Grant No.41490635 to Professor Huiming Bao.

Compliance with ethical standards

Conflict of interestOn behalf of all authors,the corresponding author states that there is no conflict of interest.