函数应用题解题策略的探讨分析

☉江苏省苏州市苏州工业园区星澄学校 吕 琴

应用一次函数的相关知识解决实际问题是中考的考查要求，函数应用题也成为近几年中考的热点问题.该类问题的求解需要明确考题立意，结合相应的基础知识，从联系性角度加以解决.本文将以一道一次函数应用题为例探讨解题策略，并进行考题拓展，与读者交流学习.

一、试题呈现

（2018年江苏省苏州市中考数学第28题）如图1，直线l表示一条东西走向的笔直公路，四边形ABCD是一块边长为100米的正方形草地，点A、D在直线l上，小明从点A出发，沿公路l向西走了若干米后到达点E处，然后转身沿射线EB方向走到点F处，接着又改变方向沿射线FC方向走到公路l上的点G处，最后沿公路l回到点A处.设AE=x米（其中x＞0），GA=y米，已知y与x之间的函数关系如图2所示.

（1）求图2中线段MN所在直线的函数表达式.

（2）试问：小明从起点A出发直至最后回到点A处，所走过的路径（即△EFG）是否可以是一个等腰三角形？如果可以，求出相应x的值；如果不可以，请说明理由.

图1

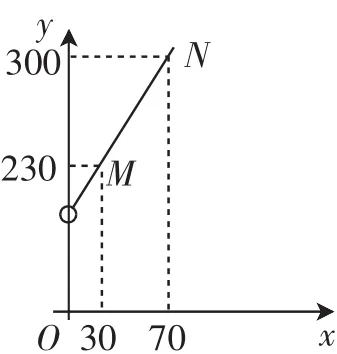
图2

二、策略探析

函数应用题与常规函数题相比最为突出的特点是重在应用，与生活实际结合紧密，该类问题的求解需要采用相应的解题策略，可分以下三步进行：

第一步：明确考题的考查立意

明确考题立意是求解函数应用题的前提条件，即通过读题反复推敲考题的问题条件，从中提取出关键信息，理解命题的立意.只有理解了立意，才能把握问题求解的方向，进而采用相应的解题思路，提高解题效率.另外，在读题时需要把握考题的性质，如确定涉及的图形、函数类型，以及问题的基本形式.

如上述考题涉及了两幅图，图1是基本的几何图形，表示小明的运动轨迹，图2是一次函数图像，表示公路l上相关距离的对应值，即AE与GA的关系，用以确定点A的具体位置，对应的两个问题分别考查函数和几何相关知识.

（1）本小题求函数的解析式，实际上考查的是函数图像上点的读取，以及图像与函数的解析式的关系，需要我们掌握图像上点的坐标到解析式的求解过程，即利用点的坐标求解析式的特征参数.

（2）本小题分析小明所走路线是否可以构成等腰三角形，从等腰三角形的判定条件出发，可以获得两种思路：一是存在等角，二是存在等边.考虑到问题中只出现了路径、长度条件，因此需要研究边长来完成求解，实际上就是考查等腰三角形的特性.

第二步：重视考题的基础知识

函数应用题一般是相关数学知识的综合，如几何图形、函数图像、代数方程、基本不等式等，其中最关键的还是函数知识，理解函数的基本性质和应用条件是求解函数应用题的基础.需要注意的是，函数应用题是在基础知识上的整合、拓展，因此只有充分掌握相应的基础知识，才能实现函数应用题的快速求解，其中包括函数性质、数学模型、研究方法.

对于上述考题，需要基于考题立意，根据问题条件思考、调用基础知识，如第（1）问求解的是一次函数的解析式，需确定函数解析式中的k和b，已知函数上的关键点，由函数图像性质可知图像上的点满足函数的解析式，故只需要将点的坐标代入解析式即可，使用的方法是待定系数法，具体过程如下：

由图像可知点M和N的坐标分别为（30，230）、（100，300），设线段MN所在直线的解析式为y=kx+b，将点M和N的坐标分别代入，得所以MN所在直线的函数表达式为y=x+200.

而对于问题（2），求x为何值时△EFG为等腰三角形，需要分析三角形内存在的等边关系，然后确定x的值，考虑到题干信息没有对△EFG的等边进行约束，因此需要采用分类讨论的方式，分别讨论FE=FG、FG=EG、EG=FE时的情形，分析其合理性，其中涉及的基础知识有几何性质、解方程等.

第三步：加强考题的知识关联

函数应用题实际上也是综合问题的代表，涵盖了多领域的知识，如上述考题涉及了几何与函数知识，而两者之间存在着紧密的联系，求解时需要准确把握知识的联系性，构建相应的解题思路.另外，对知识的整合过程，也有利于知识的进一步内化和吸收，有利于形成系统的知识体系.

如上述考题的第（2）问，求解△EFG为等腰三角形时x的取值，结合之前的分类情形加以讨论：

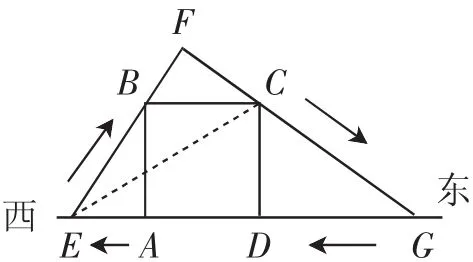
图3

①分析FE=FG成立的可能性.结合一次函数的解析式y=x+200，AE=x，GA=x+200，连接CE，如图3所示，由于AD=100，可得ED=GD=x+100.又因CD⊥EG，则△CEG是以点C为顶点的等腰三角形，即CE=CG.根据等角对等边的性质，可得∠CEG=∠CGE，则∠FEG≠∠FGE，故FE=FG不可能成立.

②分析FG=EG成立的可能性.四边形ABCD为正方形，则BC∥EG.根据平行线的性质，可得∠FBC=∠FEG，∠FCB=∠FGE，则△FBC △FEG.首先假设FG=EG.由三角形相似的性质，可推得FC=BC=100.因为AE=x，结合一次函数的解析式，可得GA=x+200，则DG=GA-AD=x+100，FG=EG=EA+AG=2x+200，则CG=FG-CF=2x+100.在Rt△CDG中，根据勾股定理，得CD2+DG2=CG2，可构建关于x的方程，即1002+（x+100）2=（2x+100）2，解得x1=-100（该值为负值，舍去），x=，所以当x等于时，有2FG=EG，此时△EFG为等腰三角形.

③分析EG=FE成立的可能性.分析思路同②，根据正方形的性质可以证明△FBC △FEG.假设EG=FE.同理可得BE=EF-FB=2x+100.在Rt△ABE中，根据勾股定理，得AB2+AE2=EB2，代入对应边长构建方程，即1002+x2=（2x+100）2，解得x1=0（点A和点E不能重合，故舍去），x=-（该值为负值，舍去），即没有满足条件的x2值，故不存在EG=FE成立的可能性.

三、拓展考题

上述考题是与平面几何相结合的一次函数应用题，属于运动问题，中考对于一次函数应用的考查也常从方案设计的角度进行，即给出相关一次函数的图像，通过对图像的分析确定问题解决的方案，求解时需要采用代数分析的方式，通过列方程、不等式转化变形等方式求解.

考题：某果园为了更新树种，准备购买A和B两个品种进行育苗配栽，如果购买两种树苗的总数为45棵，A种树苗为7元一棵，图4为B种树苗购买所需的费用y（元）与数量x（棵）之间的函数关系图.

（1）试求y与x的函数解析式.

（2）如果要求购买B种树苗的数量不能超过25棵，且不少于A种树苗，试设计购买方案，要求所用的费用最低，并求出最低费用.

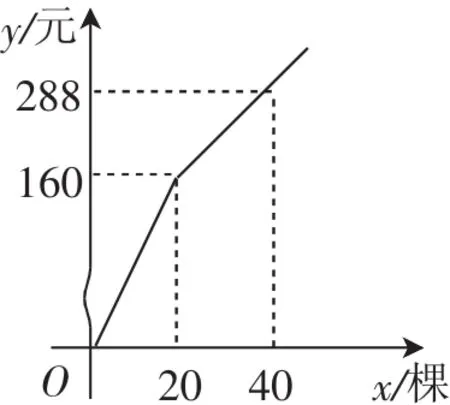
图4

分析：本题同样为一次函数应用题，与第一道考题的区别在于该题目为方案设计类，需要根据一次函数的解析式设计出最优方案，考查内容涉及一次函数的性质和不等式等知识.第（1）问为常规的函数表达式求解，采用待定系数法即可.对于第（2）问，则需要根据题干条件构建不等式组，然后构建研究总费用的函数模型，最后结合一次函数的性质求解.

解：（1）设y与x的函数关系式为y=kx+b，取图像上的两个点（20，160）、（40，288），将其代入解析式，可得

（2）根据条件“购买B种树苗的数量不能超过25棵，且不少于A种树苗”，可得不等式组22.5≤x≤25.设购买树苗的总费用为F，则F=6.4x+32+7（45-x）=-0.6x+347.F是关于x的函数，其斜率为负数，则F的值随着x的增大而减小，故x在取值范围内取得最大值时，F获得最小值，即购买树苗的费用最低.当x=25时，F取得最小值332，即最低费用为332元.

四、归纳与总结

一次函数应用题涉及众多的知识点，如一元一次方程、二元一次方程组、一元一次不等式及平面几何知识等，但问题求解的基础依然是对一次函数相关内容的理解，包括定义、解析式、性质、图像等，对其进行总结归纳，对于解题策略的形成有着重要的意义.

1.特征参数

一次函数的表达式含有两个特征参数：k和b，因此对于某一未知的一次函数，取两个满足该函数解析式的点的坐标，采用待定系数法构建二元一次方程组即可确定其解析式.其中特征参数k表示的是函数的斜率，而参数b表示函数在x轴上的截距.

2.图像与性质

对于一次函数函数y=kx+b，其特征参数k决定了函数的增减性，而参数k和b则直接控制函数在平面坐标系中的分布，因此在分析函数性质及象限分布时，只需确定特征参数的符号.另外，对于斜率k，其绝对值越大，表示y随x的变化越快，则图像的斜度越大.

一次函数应用题作为衡量学生知识应用能力的一项指标，是对“知识源于生活，又服务于生活”理念的体现，考题中涉及众多的知识点，对于学生巩固基础知识，加强知识联系，有着极大的帮助.另外，一次函数应用题的解题过程是“实际问题”向“数学模型”抽象的过程，渗透于考题中的数学思想可以在潜移默化中提升学生的解题思维，促进学生解题策略的形成，学习和掌握该类问题对于学生综合素养的提升有着重要意义.