模型归一，玩转概率

☉山东省聊城文轩中学 许 玲

2018年中考尘埃落定，各地中考试卷相继出炉，作为一线教师，研究当地近几年中考试卷的命题特点必为日后的教学与2019年的中考提供诸多有价值的帮助.概率作为各地中考中重要的一部分内容，在中考中占分约8%.笔者对此类考题进行了深入研究，感悟颇深，认为通过“模型归一”的理念可以将此类题的实质凸显出来、提炼出概率的本质，通过一个模型可以解决日后中考中诸多概率考题.今年的南京中考试题中概率考题正好就是笔者一直推崇的“模型归一”的模型，故撰文与同行交流.

一、试题类型

各地对“概率”的考查主要体现在两个层面，一是通过大量重复试验用频率估计概率；二是从事件本身发生的可能性计算概率.

用频率估计概率的考题通常以选择题、填空题形式呈现.试题呈现方式主要是在具体的问题情境中，利用大量反复实验的频率估计相应的概率，这种考查方式检测学生对概率的认识.

从事件本身发生的可能性计算概率的考题多以实际问题为背景，通常以解答题形式呈现.题目在具体的问题中让学生通过列表、画树状图等方法列出简单随机事件所有可能的结果，从而求得事件的概率.这样的考题要求学生用数学的眼光看世界，并能用数学知识和方法解决周围的实际问题，对学生理解概率的本质有着促进作用.

二、“模型归一”的实践

1.模型归一的意义

模型归一，就是将概率问题中的众多问题用一个容易理解的模型加以概括，将复杂的题目转化成熟悉的、典型的模型，从而让学生学一题会一类，使课堂高效.事实上，在概率考题中，各地中考常以“掷骰子”“摸球”“转盘”等载体呈现，“摸球”对学生来说是最熟悉不过的载体，于是所有问题不妨都归纳为“摸球”，这就是模型归一.

2.模型归一的尝试

笔者深入研究过南京市近几年的中考概率试题，均以生活为背景进行考查，这也符合《义务教育数学课程标准（2011年版）》特别强调数学背景的“现实化”，倡导学生用数学的眼光看世界，并能用数学知识和方法解决周围的实际问题.现以南京市多年来“概率”考题为例，讲述一下模型归一的运用.

例1（2012年南京）甲、乙、丙、丁4名同学进行一次羽毛球单打比赛，要从中选2名同学打第一场比赛，求下列事件的概率：

（1）已确定甲打第一场，再从其余3名同学中随机选取1名，恰好选中乙同学；

（2）随机选取2名同学，其中有乙同学.

分析：本题的亮点是贴近生活实际，以羽毛球比赛为背景呈现试题，让学生容易理解，能公平、公正地考查学生对概率本质的理解.

该题可以借助模型归一的思想加以改编：

一只不透明的盒子中装有颜色分别为红、黄、蓝、白的球各1个，这些球除颜色外都相同.

（1）从盒子中随机摸出2个球，已知1个球是红球，则另1个求球恰好是黄球的概率是多少？

考虑实际噪声情况，在仿真回波数据上叠加高斯白噪声分别使其信噪比SNR=0，10 dB，目标运动速度从0 m/s线性递增至300 m/s，FFT点数为512，采用互相关FFT法进行速度粗估计，Matlab仿真结果如图1所示。信噪比为10 dB时，测速误差基本维持在3 m/s以下，仅能满足二次相位的速度补偿误差。但当信噪比降为0 dB，速度估计值出现较大不规则波动，单独使用互相关FFT法已无法满足精度要求。因此，通常仍需在所得速度粗估计基础上进行速度精确补偿。另外，速度估计误差包络大致呈三角状，主要由FFT的栅栏效应所导致，该问题可以用Rife相关算法来得到优化[8]。

（2）从盒子中随机摸出2个球，其中有黄球的概率是多少？

例2（2014年南京）从甲、乙、丙3名同学中随机抽取环保志愿者.求下列事件的概率：

（1）抽取1名，恰好是甲；

（2）抽取2名，甲在其中.

分析：本题与2011年的考题类似，2011年的考题是选拔青奥会志愿者，此题是选拔环保志愿者，此题不仅考查学生运用概率知识，而且渗透笔者提倡的模型归一的考法，异曲同工.

该题可以借助模型归一的思想加以改编：

在一个不透明的盒子里共有3个球，1个红球，1个黄球，1个白球，它们除颜色外均相同.

（1）从盒子中随机摸出1个球，恰好是白球的概率是多少？

例3（2016年南京）某景区7月1日—7月7日一周天气预报如下.小丽打算选择这期间的1天或2天去该景区旅游.求下列事件的概率：

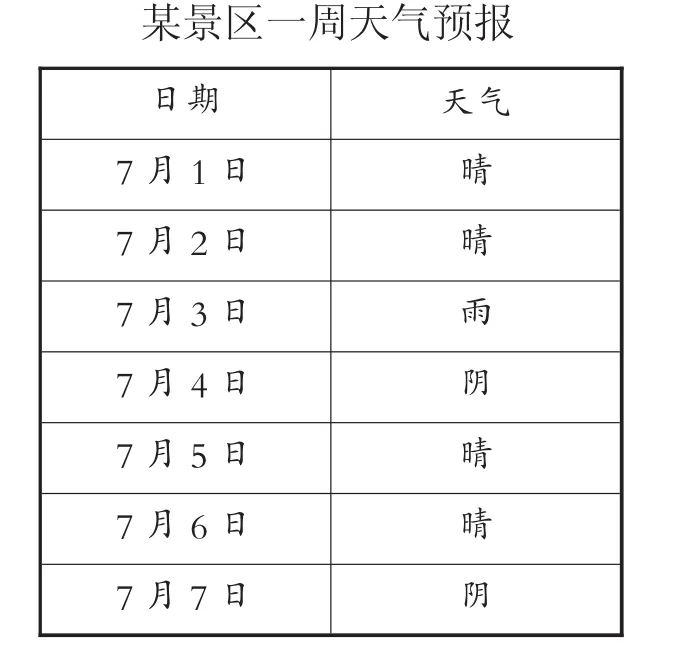
图1

（1）随机选择1天，恰好天气预报是晴；

（2）随机选择连续的2天，恰好天气预报都是晴.

分析：本题的亮点就是新颖，与前几年的考题有明显的区别，此题的模型是连续的，若学生不能发现，则容易做错.

该题可以借助模型归一的思想加以改编：

在一个不透明的长形盒子里排列着7个球，它们除颜色外均相同，7个球的颜色分别为“红红黄绿红红绿”.

（1）从长形盒子中随机取出1个球，该球是红球的概率是多少？

（2）从长形盒子中随机取出连续的2个球，均为红球的概率是多少？

例4（2018年南京）甲口袋中有2个白球、1个红球，乙口袋中有1个白球、1个红球，这些球除颜色外无其他差别，分别从每个口袋中随机摸出1个球.

（1）求摸出的2个球都是白球的概率.

（2）下列事件中，概率最大的是（ ）.

A.摸出的2个球颜色相同

B.摸出的2个球颜色不相同

C.摸出的2个球中至少有1个红球

D.摸出的2个球中至少有1个白球

分析：本题正好就是模型归一中的摸球模型，本题的亮点是第（2）问，与前几年的考题有明显的区别，看似简单，但要算出每一种情况下的概率，要求很高.

三、模型归一的思考

纵观南京市近几年中考概率试题，题目难度适中，联系实际，稳中有变，适度创新，主要考查学生的基础知识和基本技能，因此在中考备考复习中，运用模型归一的解题策略，能让学生学起来事半功倍.

利用模型归一的解题策略做题，可以将很多复杂、较难理解的问题转化成简单、易于理解的问题.主要可以归纳为4种常见模型：

（1）在一个不透明的盒子里共装有m个球，除颜色外均相同，随机摸1个球后记录颜色将其放回，求再随机摸1个球出现某颜色的概率.

（2）在一个不透明的盒子里共装有m个球，除颜色外均相同，随机摸2个球，求出现某颜色的概率.

（3）在多个不透明的盒子里共装有m个球，除颜色外均相同，求在每一个盒子里各随机摸1个球出现某颜色的概率.

（4）在一个不透明的盒子里依次排列着m个球，除颜色外均相同，求连续拿出几个球，出现某颜色的概率.（此类模型常解决抽取连续的日子等连续概率的问题）

概率问题的解决，在注重基础知识和基本技能的前提下，应提倡模型归一方法的运用，淡化对形式化记忆的考查，适当加强对具体情境的理解.

模型归一解题法就如同一个钥匙，通过它可以打开一道门户，把学生引入一个完整的领域，这种解题法有利于学生快速理解题意，转化为简单的问题.其实不仅仅是南京，各省市近些年的中考题，都已经趋向于对数学能力的考查，所以教学过程中更应关注学生对解题方法、解题策略的掌握，敢于创新出好的教学方法，让学生认识数学的特点，把握其规律，真正让学生学得轻松，成绩也能提升起来.W