改编题组渐次呈现，对话追问促进理解——以2018年两道图形翻折中考题教学为例

☉浙江省诸暨市滨江初级中学 严月华

近读《中学数学（初中版）》，三位老师围绕图形翻折设计了中考微专题复习课（见参考文献［1］～［3］），读来很受启发，这种主题聚焦式的复习课围绕一个“题干”多角度设问，是一种有效的复习课型.带着这样的思考研究各地中考试卷时，发现不少地区都将翻折问题作为综合题进行考查.本文选择两道翻折变换综合题构思一节专题复习课，供研讨.

一、图形翻折专题复习课

本课两道例题改编自2018年中考卷翻折题，改编成题组呈现.

例1如图1，将等腰直角三角形ABC对折，折痕为CD.展平后，再将点B折叠至边AC上（不与A、C重合），折痕为EF，点B在AC上的对应点为M.设CD与EM交于点P，CD与FM交于点O，连接PF.已知BC=4.

（1）求∠EMF的度数.

（2）若点M为AC的中点，求△CMF的周长和面积.

（3）在（2）的条件下，求证：PF=PM.

（4）小明发现：不需要（2）中的条件“点M为AC的中点”，也可证出△PFM的形状是等腰直角三角形.请判断小明的发现是否正确，并说明理由.

（5）随着点M在AC边上的不同位置，分析△PFM的周长的取值范围.

（6）探究FC、PC、CM三条线段之间的数量关系.

教学预设：前两问不难解决，主要是第（3）问，学生可以从两个角度进行突破.第一个角度着眼于相似，先证△POM △FOC，得出比例式，结合对顶角∠POF=∠MOC，可得△POF △MOC，于是∠PFO=∠PCM=45°，于是△PFM为等腰直角三角形.第二个角度是，识别点P、M、C、F共圆，从而根据圆周角性质可得∠PFM=∠PCM=45°，∠PMF=∠PCF=45°，问题获证.而这两种证法都没有用到条件“点M为AC的中点”，相应的第（4）问“小明发现”是正确的.

第（5）问需要考虑点M在边AC的两个端点“临界”情况.当M与C重合时（注意：根据题干要求，它们是不可能重合的，这只是讨论的“临界”情况），F为BC的中点，CF=BC=2，PM=PF=，此时△PFM的周长为2+2；当M与A重合时，F与C重合，E与D重合，FM=AC=4，PM=PF=2，此时△PFM的周长为4+4.又B不与A、C重合，所以△PFM的周长的取值范围是大于2+2且小于4+4.

第（6）问是一个经典问题，可以有多种处理方法，比如基于“旋转”的念头，如图2，作HP⊥CP交BC于点H，证出△PHF △PCM，于是证出△CPH为等腰直角三角形，从而CH=PC.又CH=CF+FH=CF+CM，则CF+CM=PC.

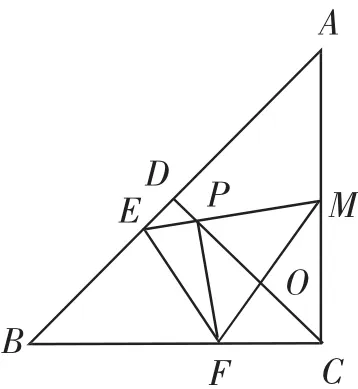
图1

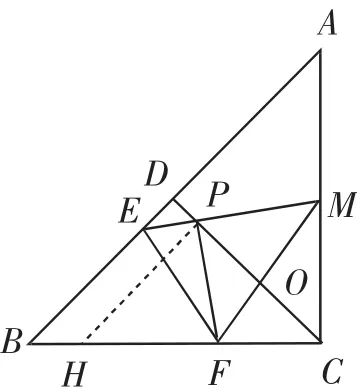
图2

例2 有一张矩形纸片ABCD，AB=4，AD=9.

（1）如图3，点E在这张矩形纸片的边AD上，将纸片折叠，使AB落在CE所在直线上，折痕设为MN（点M、N分别在边AD、BC上），利用直尺和圆规画出折痕MN.

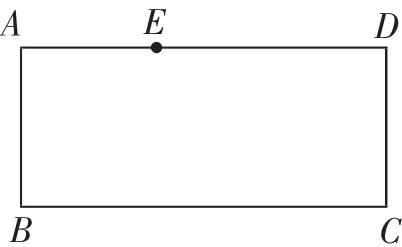
图3

图4

（2）如图4，点F在这张矩形纸片的边BC上，将纸片折叠，使FB落在射线FD上，折痕为GF，点A、B分别落在点A′、B′处.小睿发现，△FDG是一个等腰三角形，你觉得他的发现有道理吗？请说明理由.

（）如图 ，设该矩形纸片的边 上有一点 ，且45ADKDK=3，沿折痕HI折叠纸片，使AB落在CK所在直线上，点A、B分别落在点A′、B′处，小杰认为连接B′D，则DB′恰为△CDK的高.他的判断是否正确？请说明理由.

图5

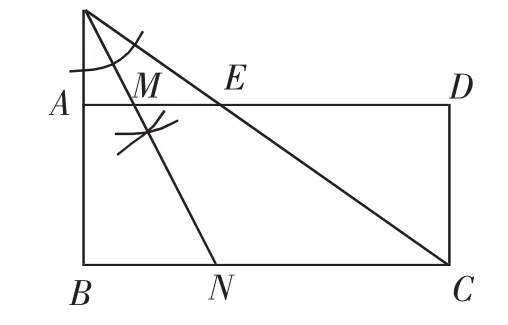
图6

预设讲评：（1）延长CE、BA形成一个锐角，如图6，作该锐角的角平分线交矩形的一组对边于M、N，则M、N为所求的折痕.

（2）根据“平行遇上平分”可得出∠DGF=∠DFG，从而确认△FDG是一个等腰三角形.

Rt△CDF中

讲评之后，还可成果扩大，追问学生：是否可求出B′D的长？预设：BF=BC-CF=9-=. 由折叠得B′F=BF=.即B′D=DF-B′F=-=3.

（4）小杰的判断不正确，理由如下.如图7，连接ID.

在Rt△CDK中，KD=3，CD=4，求出CK=5.

由折叠得IB=IB′=4k.所以BC=BI+IC=4k+5k=9k=9.解得k=1.说明△CDK △IB′C，则IC=5，IB′=4，B′C=3.把目光转向Rt△ICB′中，tan∠B′IC=

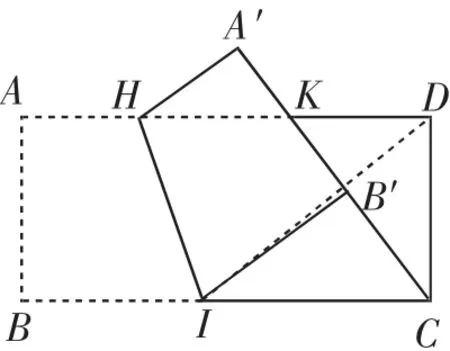
图7

二、解题教学的三点思考

1.深刻理解考题考查意图，恰当改编预设题组渐次呈现

教师解题时不能满足于思路贯通、答案获取，也不只是简单追求一题多解，而要更进一步，达到深刻理解考题的追求.何谓深刻理解考题？应该有如下表征：其一，不但有一题多解的探求，更有“殊途何以同归”的结构揭示；其二，想清辨明考题的主要难点与关键步骤；其三，站在该题在全卷的“位置”来理解命题专家设置该题的意图，以便在解题教学设计时改编题组，选择增设铺垫问题还是继续成果扩大、拓展提升.顺便指出，这里改编预设题组时，需要教师平时注重修炼自身的命题功夫.

2.教学时注重对话与追问，促进学生自主获得思路贯通

当考题经过课前的改编，以题组形式渐次呈现（所谓渐次呈现，就是每次出示一个小问，师生解决之后，再出示下一个，而不是整体推出所有小问）在课堂上时，教学进程中教师需要注意对话和追问.每呈现一个小问后，先安排学生独立思考，有多个学生都贯通思路之后，教师可安排他们在小组内先交流讲解，然后全班汇报展示，教师进行追问和评析，这时相机引导或追问其他学生对解题过程中某个关键步骤、重要信息是如何理解的，可以看出学生是否达到了真正的理解.

3.关键步骤不宜轻轻滑过，让学生有充足时间消化和理解

数学较难习题求解的障碍往往出现在起点不清、方向不明，这时教师根据课前对考题的深刻理解，出示一些铺垫式问题，可以帮助学生攻克难点.而在关键步骤的讲评过程中，也不宜轻轻滑过，忌用“显然”“易得”这类“一带而过”的教学用语，根据教学经验，学生往往没听懂、还不理解的原因多是教师在讲评过程中（或一些网传解答）出现的一些“显然”“易得”之处.为了把关键步骤如何得到，怎样自然而然地捕获解题念头讲清楚，可以安排一些优秀学生介绍他们的经验，让学生启发学生，让不同的学生表达不同的思考，一方面，可看到这些问题的处理视角或着眼点，另一方面，拉长思考过程，也为学生赢得充足的时间消化和理解.