船用钢板高频感应加热热源简化计算方法

张正星，赵耀，胡小才，杨振

华中科技大学船舶与海洋工程学院，湖北武汉430074

0 引 言

在造船工业中，船舶外板的加工通常采用线加热工艺。该工艺是一种沿预定的加热线对板材进行局部线状加热的方法，采用水跟踪冷却（或自然冷却），使板材产生局部塑性变形，从而将其弯成需要的曲面形状。传统的线加热工艺使用的是氧乙炔火焰作为热源对钢板进行加热。随着技术的发展和造船模式的转变，高频感应加热因效率高、精度较易控制和更环保等特点，在很多工业领域得到了广泛应用。作为一种线加热工艺的热源，高频感应加热也受到越来越多研究人员的关注。例如，Neki等［1］针对高频感应加热工艺，运用有限元法和热弹性塑性理论，对温度场分布及计算变形量进行了分析，通过与实验数据比较，发现两者基本一致，但该研究仅在理论基础上进行了计算，并未建立数值模型，且针对的是静止式感应加热；Luo等［2］在建立的钢板感应加热平面热源模型的基础上，通过加载热源模型的方式，模拟了平板感应加热过程中的温度分布和固有应变，但并未涉及感应器在移动加热时的电磁场计算过程；Baek等［3］将感应加热中的电磁场和温度场分开来求解，首先通过电磁分析和计算得到热通量，再加载到计算模型中，进而求解钢板的热分布，但求解的方法简化了电磁场和温度场的双向耦合过程，热源模型的热流密度分布与实际热源相差较大。

针对移动式热源加热过程的数值模拟计算，研究人员在焊接、激光加热等领域对其进行了大量研究。例如，Cheng和Lin［4］建立了移动式热源加热过程的三维温度场解析模型，将热源设定为沿平行于矩形板的板边方向移动，在移动中使用高斯热源模型模拟移动热源。Araya和Gutierrez［5］建立了钢板激光加热过程中温度场分布的计算模型，同样使用高斯热源模拟激光束热源。

高频感应加热热源受感应器几何形状和加热参数等诸多因素的影响，且与工件的温度关系密切，难以用一个恒定的热源来替代。移动式感应加热过程涉及多个物理场间的耦合，若要建立准确的数值模型非常困难。而杨玉龙［6］建立的移动式感应加热数值模型是通过小步距、间歇式移动式感应器来模拟连续的移动加热过程，该模型尽管考虑了电磁场和温度场的磁热双向耦合，但却十分复杂，耗费的计算资源和时间巨大。在感应加热数值计算中，通常采用的是（电）磁热耦合方法［7-11］。该方法准确性高，但模型过于庞大且复杂，尤其是应用于移动式感应加热的数值计算时，也存在计算资源和时间耗费巨大的问题。

本文将提出一种针对高频感应加热热源的简化计算方法，通过分析加热过程中电磁场和感应电流的分布特性，以一个空间函数形式的热源模型来代替复杂的磁热耦合计算，通过比较上述两种方法得到的温度场分布，对该热源模型应用于静止式感应加热数值计算中的可靠性进行验证。

1 高频感应加热热源模型研究

目前，国内外各大船厂主要使用线加热工艺来加工船体外板。对于线加热工艺的研究，早期的方法是通过对大量钢板的实际加工测量来掌握船体外板的变形规律。这种方法虽然得到的结论真实可靠，但参数非常多，若要掌握各项参数对钢板变形的影响，需开展大量的实验，准备工作繁杂，人力和物力消耗巨大，成本相当高。随着计算机数值模拟技术的迅速发展，其优势明显大于实验方法，故得到了广泛应用。目前，线加热工艺的研究多以数值模拟为主，再辅之以实验方法来进行验证。对于高频感应加热的数值模拟，广泛得到运用的是磁热耦合方法［12］。

1.1 磁热耦合计算方法

图1所示为磁热耦合计算方法流程图。该方法的主要计算步骤如下：

1）建立模型，包括建立钢板、感应线圈及周围空气的模型，输入材料属性，施加载荷及设置边界条件。

2）设置物理场的初始环境，即电磁场和温度场。

3）读入电磁场物理环境，求解得到钢板中生热率的分布。

图1 磁热耦合计算流程图Fig.1 Flow chart of electromagnetic-thermal coupling calculation

4）读入温度场物理环境。

5）读入电磁场求解得到的生热率。

6）求解温度场，得到钢板温度分布。

7）判断求解是否结束，若结束，可得到钢板温度分布的计算结果；若未结束，则进入步骤8）。

8）判断是否更新电磁场材料属性，若需要，则利用求解得到的钢板节点温度来更新电磁场的材料属性，并重复步骤3）；若不需要，则进入下一个载荷步求解，并重复步骤4）。

从上述方法可知，在运用磁热耦合方法进行计算时，需要先建立电磁场和温度场物理环境，然后再进行计算，而计算每个物理环境得到的结果又是另一个物理环境的载荷。该方法得到的结果虽较准确，但耗时过长。

对于运用磁耦合方法计算移动式加热过程，要求感应器在钢板上方移动。此外，还需在计算过程中重新建立模型以及划分网格。这会使得计算模型十分庞大和复杂，需要消耗大量的计算资源和时间。所以，本文提出了代替感应加热耦合计算的热源简化计算方法，可同时解决磁热耦合计算模型过于复杂及计算时间过长的问题。

1.2 热源模型空间函数建立

钢板感应加热模拟计算的本质是求解得到热量分布，然后将热量分布加载到计算模型中的钢板上，进而计算钢板的温度场，最后得到钢板上的温度分布。因此，若能得到热量分布并直接加载到钢板模型上进行运算，则仅需创建钢板模型，无需为巨大的空气域和复杂的感应器进行建模，故可明显降低模型复杂度，提升计算速度和效率。

1.2.1 感应加热原理简介

感应加热的热量主要来源于涡流损耗的焦耳热效应［13］。任意导体中通过电流时都会在其周围空间和导体内部激发磁场；恒稳的电流产生恒定磁场，交变的电流产生交变磁场，在此感应线圈中的零件（部件）会被此交变磁场所切割［14］。根据电磁场理论，变化的磁场会产生感应电动势ϕ，用法拉第电磁感应定律则可表示为［15］

式中：E为电动势；l为任意截面或范围的回路电流。

由于存在感应电动势，在零件表面薄层内将形成封闭的电流回路，通常把这种电流称为涡流。假设回路中的涡流强度为I，电阻为R，则根据焦耳定律，在时间t内，回流中产生的热量Q即为

钢板的高频感应加热方式基本上分为2种：静止式加热和移动式加热［16］。前者指感应器在整个加热过程中无需移动，等加热到一定温度后再移开感应器，然后再对钢板进行冷却的加热方式；后者则类似于氧乙炔火焰的加热方式，加热时感应器以一定的速度和路径在钢板上方移动。

1.2.2 高频感应加热的集肤效应

对钢板感应加热热源进行热量分布计算，需要对感应加热热源的特点有一定的了解。在计算中，加载热量采取2种方式：一种是将生热率作为体热源进行加载；另一种是将热流密度作为表面热源进行加载。钢板感应加热热源来自电磁感应在钢板上产生的无数涡流。根据焦耳定律，具有一定电阻的钢板在加热过程中会产生热量，使其温度升高。该电磁感应加热产生的感应电流主要集中于钢板表面厚度很薄的一层中，此现象被称为“集肤效应”。这层感应电流分布在钢板表面上的厚度被称为“集肤深度”，并可由下式计算：

式中：δ为集肤深度，mm；ρ为钢板的电阻率，Ω·m；f为电流频率，Hz；μ为相对磁导率，H/m。

本文计算表明，钢板上加热的热量约有90%处于集肤深度内。以电流频率为12.7 kHz的Q345钢板为例，按照式（3）计算得到的钢板集肤深度仅约1 mm。而船体外板厚度一般在10 mm以上，相对于船体外板厚度，该集肤深度非常小，故可将该热源简化为表面热源来处理。表1和表2给出了Q345钢材料在不同温度下的特性。

表1 不同温度下Q345钢的电阻率Table 1 The resistivity of Q345 steel at different temperatures

表2 不同温度下Q345钢的相对磁导率Table 2 The relative permeability of Q345 steel at different temperatures

1.2.3 热流密度空间函数

由上文可知，高频感应加热的原理是感应加热线圈中交变电流与钢板之间互感，在钢板表面薄层中产生感生涡流，而钢板本身由于具有一定的电阻，从而使钢板产生热量。

若将感应线圈与钢板间互感产生的热量简化为表面热源，则需了解在感应加热过程中钢板表面的涡流分布情况。为此，本文建立了一个如图2所示的简单的钢板静止式感应加热模型，使用磁热耦合方法对感应加热过程进行计算。

图2 钢板静止式感应加热模型Fig.2 Model of static induction heating for steel plate

在感应线圈中，若电流大小和距离钢板表面的高度等条件不变，则钢板表面感应电流密度与钢板相对磁导率呈正相关关系。随着钢板温度的升高，钢板相对磁导率降低，因此钢板表面的感应电流随温度的变化而变化。如图3所示，当钢板表面中心点温度达到居里温度时，感应电流密度变为0。

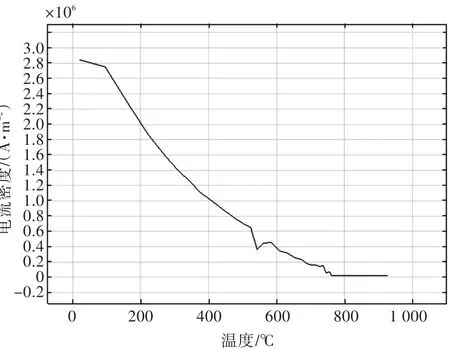
图3 钢板表面中心点电流密度随温度变化的曲线Fig.3 Variation curve of surface current density of center point on steel plate with temperatures

从钢板表面中心点可以看出该点的感应电流随温度变化的规律，但不能简单地将此规律推广到整个钢板表面。因此，如图4所示，沿钢板表面取一条截线，得到在加热过程中及不同加热时间之后，钢板在这条截线上的感应电流密度分布（图5）。

从图5可以看出，在不同加热时间下，钢板表面感应电流分布的特点是一致的，即在感应线圈正下方钢板表面附近的感应电流密度最大，然后沿两侧迅速下降。随着加热时间的增加，钢板温度不断升高，钢板表面的感应电流密度随之下降。因此，若将钢板在初始加热条件下表面的电流密度分布设为初值，再用初值乘以某个系数来代替其他温度下钢板表面的电流密度分布，就可以得到钢板表面的电流密度随温度变化的函数J(x，y，T)。其中，x，y为钢板表面坐标，T为钢板表面坐标点的温度，即钢板表面坐标点的温度范围为钢板初始加热温度到钢板居里温度。

图4 钢板表面截线示意图Fig.4 Schematic diagram of surface section of steel plate

图5 钢板表面截线上的电流密度分布曲线Fig.5 Distribution curves of current density on the surface section of steel plate

得到感应加热过程中钢板表面的电流密度函数之后，根据焦耳定律，即式（4），可以求出在钢板中的生热率分布：

式中：g为钢板中的生热率函数；J为感应电流密度函数。

此后，再将生热率函数沿钢板厚度方向进行积分，便可得到钢板表面的热流密度空间函数。

2 热源模型可靠性验证

为了验证热源模型的可靠性，分别采用磁热耦合数值计算和热源空间函数方法得到钢板温度场变化情况，并将两者的结果进行了比较，以验证热源模型的可靠性。

2.1 钢板静止式感应加热磁热耦合分析

本文使用COMSOL Multi-physics有限元分析软件进行钢板静止式感应加热的模拟仿真。在磁热耦合计算中，需要建立钢板、感应线圈和空气域有限元模型。图6所示为钢板静止式感应加热模型示意图。

图6 磁热耦合计算模型Fig.6 Model of electro magnetic thermal coupling calculation

由于感应加热时，钢板上的涡流在集肤效应作用下主要集中在钢板表面的一层内，为确保计算精度，在网格划分时至少需要在集肤深度内划分多层单元。同时，为减少计算时间，可以将靠近加热面一侧的网格划分得更密一些，而在加热背面的则可划分得稀疏一些，如图7所示。

图7 磁热耦合计算的网格划分Fig.7 Meshing of electromagnetic thermal coupling calculation

在模型中采用船用低碳钢作为加热材料，钢板尺寸为200 mm×200 mm×20 mm。感应线圈采用单匝圆形截面的紫铜线圈，内通20℃冷却水。其他加热模型参数见表3。

表3 静止式感应加热模型参数Table 3 Parameters of static induction heating model

经过计算，在加热300 s后，得到钢板的温度场分布如图8所示。

图8 磁热耦合方法计算的钢板温度场Fig.8 Temperature field of steel plate by electro magnetic thermal coupling calculation

由图8可以看出，钢板的高温区集中在钢板表面，在感应加热线圈正下方的圆环区域，最高温度达到了800℃。

2.2 感应加热热源模型方法分析

首先，使用COMSOL Multi-physics有限元软件建立上节所述模型，但仅计算钢板初始加热条件下钢板表面的涡流密度。如图9所示，感生涡流主要集中在钢板表面的圆环区域内，该圆环区域在感应加热线圈的正下方位置。

由于上述计算过程仅涉及了单一物理场，即磁场，故极大地提高了计算速度。在此基础上，利用计算得到的钢板表面涡流密度分布情况，可以获得感应加热热源在钢板表面的热流密度，进而将此转化为可在有限元分析软件中输入的热流密度空间函数，如图10所示。

图9 钢板表面的涡流密度分布Fig.9 Distribution of eddy current density on the surface of steel plate

图10 热流密度空间函数示意图Fig.10 Schematic diagram of spatial function of heat flow density

最后，使用图10所示热流密度空间函数进行计算。因为是直接将热流密度载荷加载到钢板上计算，故显著简化了钢板的建模过程。图11所示为建立的有限元模型。

图11 热源计算模型Fig.11 Calculation model of heat source

经过计算，加热300 s后得到钢板温度场分布。如图12所示，钢板高温区域都集中在钢板表面，可以看到一个明显的高温圆环，该圆环刚好位于感应线圈的正下方。

2.3 磁热耦合与热源模型计算结果对比

通过对比图8和图12可以看出，磁热耦合计算和热源模型计算这两种方法得到的钢板温度场分布一致。为继续验证热源模型的可靠性，分别在钢板中取表面中心点A和钢板内部中心点B，并对两点的温度曲线进行比较，结果分别如图13和图14所示。从两个图中可以看出，两种方法得到的温度场变化规律比较一致。

图12 热源模型计算得到的钢板温度场Fig.12 Temperature distribution of steel plate by heat source model

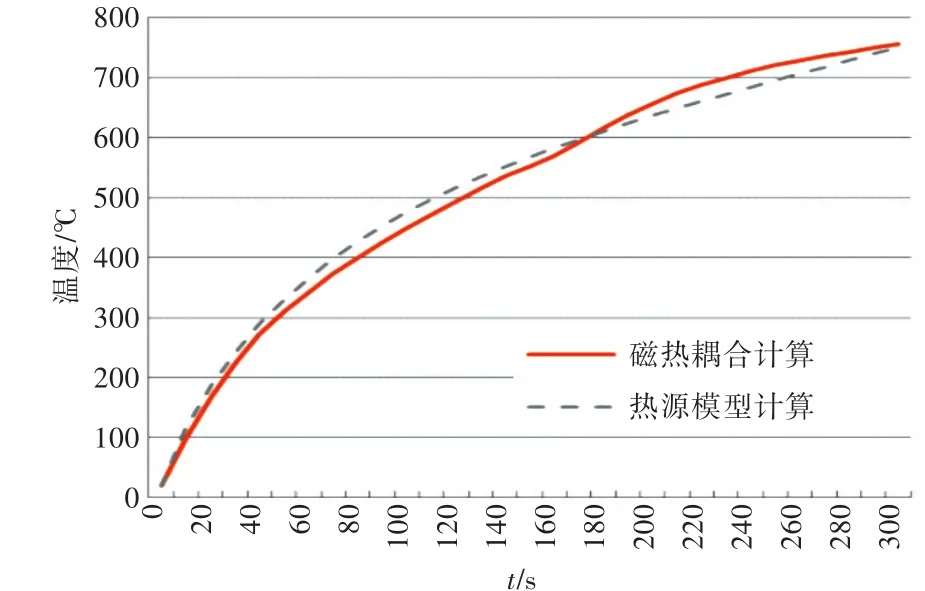
图13 A点温度变化曲线Fig.13 Variation curves of point A temperature

图14 B点温度变化曲线Fig.14 Variation curves of point B temperature

为了比较磁热耦合和热源模型这两种计算方法的计算效率，将两种方法各自模型的自由度数目和计算时间列于表4。

如前所述，磁热耦合分析不仅需要建立钢板模型，还需要建立计算感应线圈及空气域的模型，故模型中自由度数目较大。而采用热源模型进行计算，模型得到了简化，所需的计算自由度数目和计算时间显著减少。通过对比不难看出，使用热源模型计算在精度上可以满足要求，且计算效率得到了大幅度提高。

表4 磁热耦合和热源模型计算方法的效率比较Table 4 Efficiency comparisons of electromagnetic thermal coupling calculation with heat source model

3 结 语

本文针对在船用钢板高频感应加热数值计算中，磁热耦合计算方法存在模型复杂、耗时过长等问题，通过计算和理论推导，提出了一种感应加热热源的简化方法，即以一个空间函数形式的热源模型来代替复杂的磁热耦合计算。通过比较采用简化方法和磁热耦合方法计算的结果，验证了采用所提方法得到的热源模型的可靠性。同时，从两种计算方法所需时间及模型的自由度数目可以发现，简化方法计算时间明显减少，计算效率显著提高。