水下爆炸下舰艇不同部位冲击环境数值分析

董九亭，刘建湖，汪俊，刘国振

中国船舶科学研究中心，江苏无锡214082

0 引 言

作战舰艇由于其特殊的任务需求，必然要面临水下兵器爆炸带来的威胁。相比于接触爆炸造成的结构损坏，非接触爆炸会造成更大范围内舰艇设备的冲击破坏，因此，研究舰艇设备的冲击环境对其抗冲击设计至关重要。国内的抗冲击标准主要参考自美国的901系列和DDS072，而这些标准与其他海军强国的标准（如德国的BV 043/85）相比有哪些区别值得深入研究。例如，我国军标GJB 1060.1要求的冲击设计谱并没有等谱位移的要求，但901系列和BV 043/85却要求采用三折线谱的形式；BV 043/85根据舰艇吨位的不同对抗冲击有不同的要求，而901系列则没有，诸如此类的问题越来越阻碍了国内舰艇抗冲击技术的发展［1］。因此，深入研究美军标与BV 043/85等的设计依据就显得越来越重要。舰船冲击环境受冲击因子、设备安装位置和安装方式等因素的影响，表现出复杂的特征。国内外很多学者通过数值仿真结合试验研究的方式，总结归纳了很多冲击环境工程化预报公式［2-5］。冲击环境在全船范围的分布规律所涉及到的影响因素很多。尹群［6］认为，从外底板到船体上部，在同一纵剖面位置处，局部结构刚度的不同会影响谱位移和谱速度值。同样的位置设置，钱安其等［7］则认为谱加速度值较谱速度值和谱位移值衰减更快。崔杰等［8］在横舱壁与中纵剖面上设置测点，得出了冲击谱值在各个横剖面随测点位置的升高呈指数规律衰减的结论。

本文将在研究不同阻尼参数对双重渐近法（DAA）冲击环境影响的基础上，用弹簧振子模拟弹性设备的安装，并从不同安装位置的角度出发对冲击环境进行研究。在冲击因子相同的情况下，通过研究冲击环境沿全船的分布规律，得到振子响应与其基座冲击环境的关系，以及同一甲板上不同位置处、同一横剖面上不同甲板处冲击环境的频率和幅值的差异。

1 计算方法

水下爆炸下，流体与结构的解耦问题是动响应分析的关键点和难点。解析法仅限于简单结构的求解，在实际工程应用中，采用近似的解耦方法更实用，其中二阶双重渐近法（DAA2）［9］因其在各个频段都有良好的精度而被广泛使用。DAA2考虑了流体的可压缩性和流动特性，相比DAA1，增加了流体模态频率矩阵，提高了中频段的精度。其主要公式如下［10］：

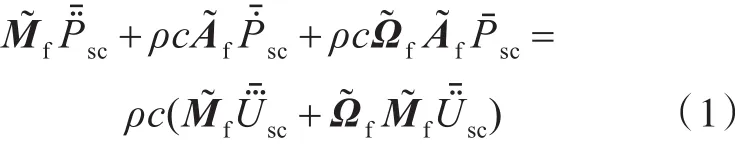
2 模型计算及参数选取

2.1 有限元模型

本文采用的模型是按照某型水面舰船的实船尺寸建立：总长59.05 m，型宽8.50 m，型深3.70 m，设计吃水2.24 m，正常排水量570 t。有限元模型建立后，先对其进行模态分析，并与激振试验得到的固有频率进行对比，结果如表1所示，证明模型可用于本文的计算。

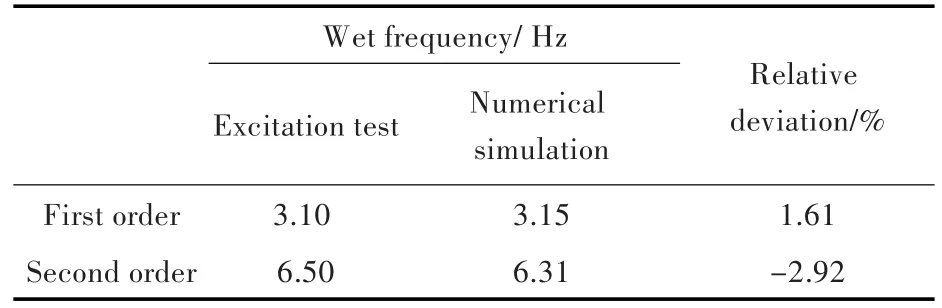
表1 有限元模型与实船激振试验湿频率对比Table 1 Comparison of wet frequency of FEM and excitation test

计算工况为：药量1 000 kg TNT沉底，距离右舷74 m，药包深度50 m，沿船长方向位于船舯位置，攻角31.4°，龙骨冲击因子0.311。

在测点方面，本文采用了设置于迎爆面的质量为200 kg、频率为5～500 Hz、按照对数等间距排布的弹簧振子模拟设备。其中，频率在15 Hz以下的弹簧振子采用0.05的阻尼比ξ，其他振子则设置为0.01的阻尼比。在内底板、主甲板和横舱壁的艏部、舯部和艉部各设一处安装位置，上层建筑由于其沿船长的特殊性，未在艉部设置安装位置。所有弹簧振子的基座均采用统一样式，避免了因基座阻抗不同所带来的振子响应谱值的差异。模型及测点布置如图1和表2所示。

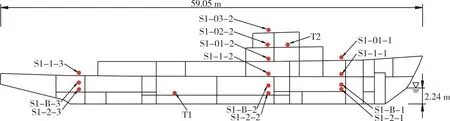
图1 测点布置图Fig.1 Arrangement of test points

表2 测点编号Table 2 Number of test points

2.2 参数确定

在DAA2方法中，流体阻尼η与瑞利结构阻尼C是影响计算结果的重要参数。根据瑞利阻尼的表达式C=αM+βK（α和β分别为控制质量M和刚度K在阻尼中贡献的系数），参考美国舰船研究院Shin等［14］获得的α和β在不同区域的取值，再结合有关η取值的模型计算经验，选取了几组组合如表3所示。

表3 双重渐进法阻尼参数取值Table 3 Damping parameters of DAA

为了验证参数选取的可信度，采用DAA2对上述不同阻尼参数组合下的整船有限元模型进行了计算。将舰船迎爆面主机基座处（图1所示测点T1）和驾驶室中线地板处（图1所示测点T2）的响应分别与实船试验对应点的实测数据进行了对比，验证结果如图2所示。根据图中所示，在2.5 Hz以下频段以及20～60 Hz频段，工况5的计算结果更加理想；在除此之外的其他频段，工况4计算得到的数据与实测数据吻合良好。从图中还可以看出，η在20 Hz以下频段影响比较明显，在20～60 Hz频段上的响应随α的变大而变小，而在300 Hz以上频段，则是β的影响更加明显。

图2 不同阻尼参数下的冲击谱Fig.2 Shock spectrums of different damping parameters

3 计算结果分析

冲击环境是设备在水下爆炸下的基础输入，是设备抗冲击研究的基础［10］。目前，应用比较广泛的用于描述冲击环境的方法是基于模态分析理论的冲击谱方法。所谓“冲击谱”，是指一系列有阻尼或无阻尼的单自由度单位质量振子，在承受同一基础冲击运动作用时，其响应的最大值与固有频率之间的关系。当考虑阻尼比ζ时，冲击位移谱为［15］：

式中：D(ω，ζ)为冲击位移谱，m；ω为圆频率，rad/m；z̈为基础加速度，m/s2。

本文分别计算了不同安装位置的振子响应谱，并与所安装基座冲击环境进行了对比。所有弹簧振子的基座均采用统一样式，避免因基座阻抗不同而带来振子响应谱值的差异。选取其中的横舱壁艉部位置作为代表，如图3所示。

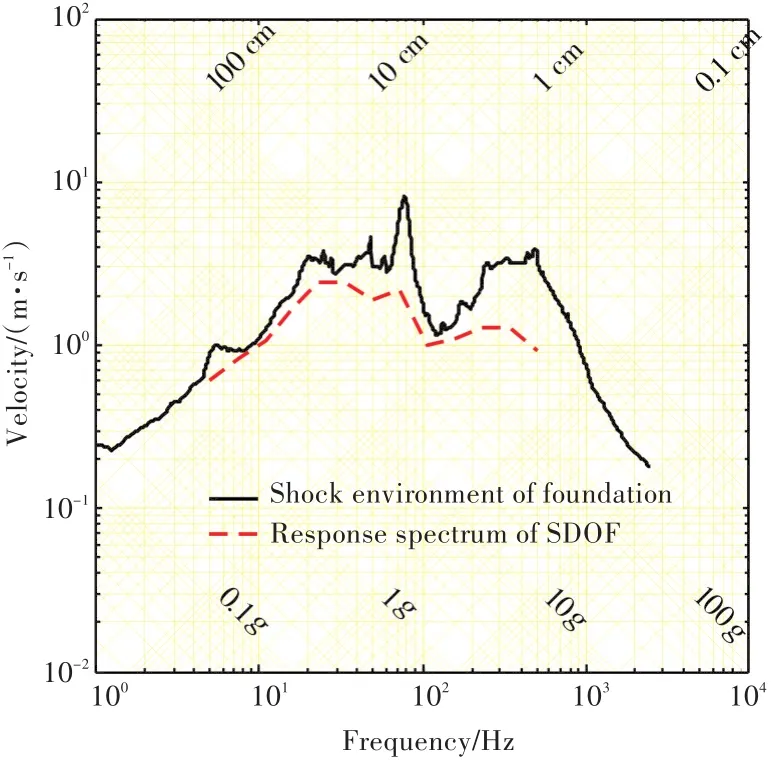
图3 横舱壁艉部位置基座响应和振子响应Fig.3 Shock environment of foundation and response spectrum of SDOF at aft of the transverse bulkhead

图4 同横剖面处不同甲板各振子响应谱比较Fig.4 Response spectrums of SDOF at different decks of the same transverse section

从图中可以看出，振子响应谱与基座冲击环境趋势一致，但前者的谱值均比后者小，并且在11 Hz以下现象比较明显。这是因为基座处冲击环境的本质是在假设其上的振子是单位质量情况下得到的冲击响应最大值，而本文采用的振子具有200 kg的质量，与66 kg的基座相比质量效应不可忽略。并且为了简化计算，振子的阻尼与结构本身的阻尼并不一致，这也是引起谱值差异的原因之一。另外，在低频段影响冲击谱的主要因素是质量，安装频率的影响不大。根据惯性力F(t)［15］的表达式

式中，F(t)为单自由度系统与基础之间的惯性力，N；m为设备质量，kg。可知设备对基础的反作用力是随刚基础频率的增加而增加的。

图4所示为同一横剖面处不同甲板的振子响应谱间的对比。从内底板到上层建筑，舯部和艉部振子响应谱的等谱位移值是逐渐增大的，这与工程实际一致。由于本例中设置的基座和振子在船艏、船舯或船艉处都位于同一横剖面上，故理论上影响振子响应的因素只有振子的垂向高度。艏部除主甲板外，其他各处的谱位移值均比较接近，并且横舱壁和内底板未形成明显的等位移段，其原因可能是艏部设置振子的地方在两个舱壁之间，整个舱室狭小，隔板和加强筋多，从而导致此处刚度偏大，从下到上各个测点响应都近似于横舱壁上的响应。而主甲板上的振子响应谱在谱位移和谱速度段均为各层甲板中的较大者，其在船舯位置处甚至还超过了某些上层建筑。这是因为主甲板在船长方向上长度很长，导致整层甲板的刚度较小，其参与中、低频段船体响应的程度较高。在各层甲板的等位移和等速度的转折频率中，横舱壁由于其较大的刚度，对应的转折频率较低，其次是内底板，然后是主甲板和上层建筑。

选取的5～23 Hz频段振子在各层甲板舯部位置的谱位移值如图5所示。由图可见，谱位移值随高度的上升而呈增加趋势。将不同频率下振子的数据用指数函数拟合，可得到如下公式形式：

式中：D为振子谱位移，cm；h为振子所在甲板高度，m；H为横剖面总深度，m。并且通过研究不同频率f下αD和βD的值，发现其值也近似符合指数规律，拟合结果为

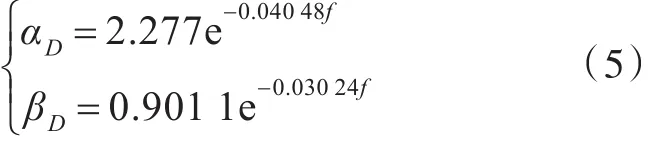
将拟合得到的公式与DAA计算结果进行对比，得到其相对偏差如表4所示。从表中可以看出，拟合公式在主甲板和横舱壁的几个频率上表现略差，但在其他甲板上其相对偏差则基本在10%以内。

图5 不同频率振子沿横剖面深度的谱位移值Fig.5 Spectrum displacement of SDOFs at the same transverse section

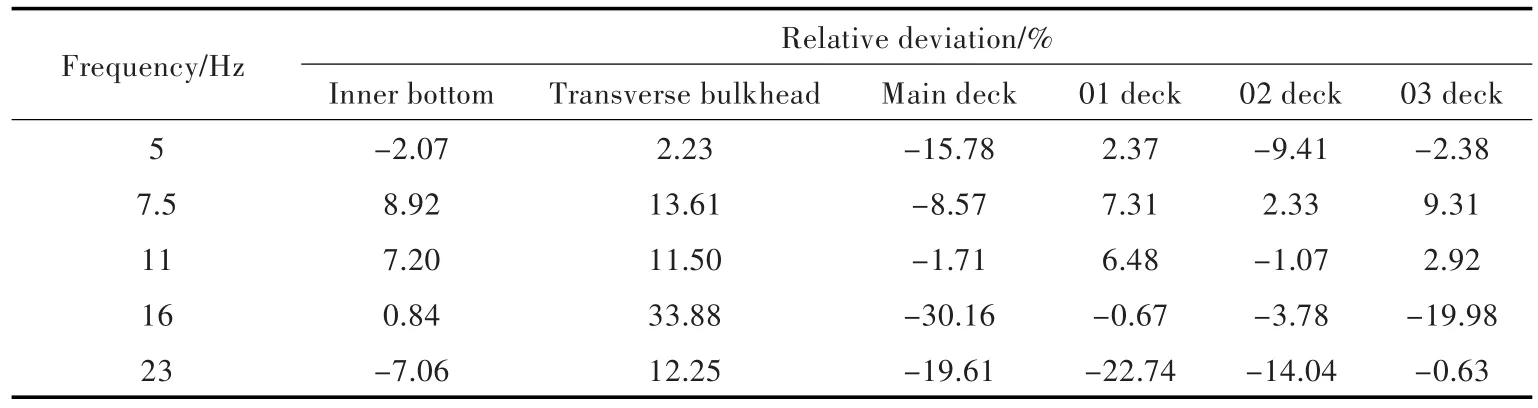
表4 谱位移拟合公式与DAA计算结果的相对偏差Table 4 Relative deviations of spectrum displacement between fitted formula and calculated results

由图5可以看出，在几个比较关注的低频段振子上，在主甲板处，都有一个明显的高于所在拟合曲线的较大谱位移值。通过对有限元模型模态的分析发现，主甲板在船舯位置存在一个参与度很高的局部振型，该振型频率为9.61 Hz，如图6所示。所以，对于该处振子的冲击响应，需在整体响应的基础上叠加局部振型带来的效应。

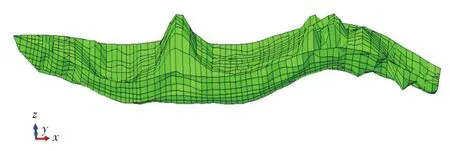
图6 主甲板船舯位置处的局部振型Fig.6 Mode shape of upper deck at ship center

而在谱速度方面，主甲板和上层建筑并没有出现较为明显的等速度段。16～50 Hz频段范围内的振子谱速度也可以采用指数函数来拟合，但不同频率之间的差异较大，23 Hz频率以下振子的响应呈指数增大趋势，而在23 Hz频率以上则是呈指数减小，如图7所示。其拟合公式也可以写作如下形式：

式中，V为振子谱速度，m/s。通过在频率范围内的拟合式的系数，可以得到

图7 不同频率振子沿横剖面深度谱速度值Fig.7 Spectrum velocity of SDOFs at the same transverse section

将式（6）和式（7）得到的结果与DAA计算得到的谱速度进行比较发现，不管是哪个频率的振子，其拟合结果与计算结果的偏差都很大。由图7中也可以看出，虽然每条曲线都有指数曲线的趋势，但是这些曲线作为一个整体的情况其规律性并不强，而且每条曲线上都有几个偏离拟合曲线距离过大的点。

在高频阶段，除舯部外，横舱壁的加速度响应是各甲板中最大的，这是因为横舱壁是强结构，其刚度非常大，易被冲击波高频分量激起较大的响应。每个频率的振子加速度响应从内底板到上层建筑均呈现指数衰减的特征，且随着频率的增大，谱加速度衰减越快。同时，加速度响应从内底板到主甲板的衰减速度明显大于在上层建筑之间的衰减速度。在73～500 Hz频段，振子谱加速度在横剖面上的变化规律如图8所示，每条曲线也都近似为指数函数曲线，可以拟合为

式中，A为振子谱加速度，g。上式中的2个系数随振子频率的变化可以拟合为

用式（9）拟合的参数计算得到的谱加速度与DAA计算的结果相比，虽然每个频率下的谱加速度曲线可以用指数曲线拟合，但若要试图用更简洁的思路去得到每条指数曲线的系数，效果并不理想。

图8 不同频率振子沿横剖面深度谱加速度Fig.8 Spectrum acceleration of SDOFs at the same transverse section

在同一层甲板上，沿船长方向不同位置处的振子对比如图9所示。由图可以看出，主甲板各振子的谱位移相对一致，但是仍与其他甲板一样表现出了从艏部到艉部逐渐变大的位移趋势。并且在10 Hz以下，艏部响应最大，舯部次之，艉部最小，而在 10～25 Hz，则是艉部最大；30 Hz以上，舯部响应逐步增大。

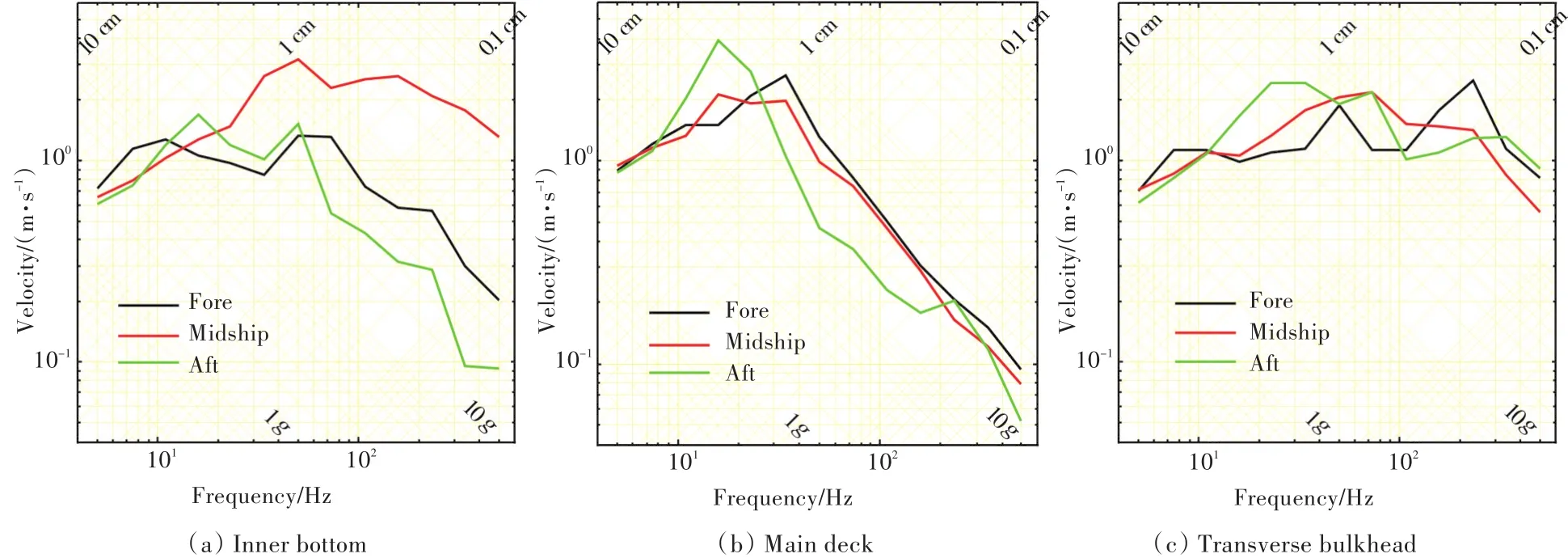
图9 同一层甲板上不同位置各振子响应谱比较Fig.9 Response spectrums of SDOF at different locations of the same deck

在中频段的速度响应方面，出现了等谱速度趋势时的转折频率，艏部最小，艉部次之，舯部最大。并且，艏部、舯部和艉部的等谱速度值从内底板到上层建筑呈增大的趋势，其与谱位移值的规律一致。而且在横舱壁，等速度段持续的频段要明显高于其他甲板，约在200 Hz以后才会出现等谱加速度的趋势。

在谱加速度方面，肿部和艏部的要比艉部的大。但是不同的甲板，等加速度段出现的频率和各谱值大小不尽相同，没有明显的规律可言。

4 结 论

本文通过建立小型水面舰船有限元模型，设置不同位置、不同安装频率的弹簧振子，采用DAA2法对其进行水下非接触爆炸下的冲击环境响应计算，分析和总结了不同位置的冲击环境特征，得到如下结论：

1）单位质量振子的响应谱值小于其基座处的冲击环境谱值。

2）从内底板到上层建筑，谱位移值和谱速度值在23 Hz以下频段表现为呈指数增大，且频率越低，增大越快；加速度谱值在50 Hz以上频段表现为呈指数衰减，衰减速度随频率的增加而增加，随甲板层数的增加而减小。

3）冲击能量在从船底向上层建筑传递的过程中，与冲击波直接接触的舱壁的冲击响应高频分量丰富，且其加速度谱值更大。

4）在内底板、横舱壁和主甲板上，艏部出现等谱速度时对应的频率最小，艉部次之，舯部最大。