怎样寻找解题的思维起点
2018-10-25杨春华
杨春华
解题就是“解决问题”,即求出数学题的答案.这个答案在数学上也叫“解”.所以,数学解题就是找出数学题的解的思维过程.解题过程就是根据问题条件,利用相关的数学基本知识、基本技能、基本思想和活动经验,有计划、有步骤、有目的地进行逻辑推理活动.它通常有4个阶段:理解题意、思路探求、书写表达、回顾反思.要快速准确地解题,选择准确的、科学的思维起点至关重要.为了便于同学们快速准确地解决数学问题,本文将以圆中的重点题型为例,对寻找初中数学解题思维起点的策略进行简单的分析,以期对同学们有一定的启迪与思考.
一、直接将题设条件作为思维起点
有同学在审题时不认真,没看清题目的条件,导致解题无从下手.防止这种情况出现的方法是,在阅读时放慢速度,对每一个条件尽可能发散思维,思考由每个条件可以得到哪些结论,再将这些结论进行融合,找到相互间的关联,从而达到解决问题的目的.
例1如图1,已知AB是⊙O的直径,点P在BA的延长线上,PD与⊙O相切于点D,过点B作PD的垂线交PD的延长线于点C,若⊙O的半径为4,BC=6,则PA的长为( ).


图1
【分析】本题考查了圆的切线性质、三角形相似条件及性质的相关知识.本题要求线段PA的长度,只需连接切点D与圆心O,则由切线性质即得OD⊥PC,再结合BC⊥PC,得结论OD‖BC,利用△POD∽△PBC的对应边成比例求出线段PA长度即可.有部分同学由于没准确提取条件“PD与⊙O相切于点D”中的“点D是切点”信息,而不能快速联想“看切点,连圆心,得垂直”这一常见添加辅助线思路.
【解答】解:连接OD.∵PD切⊙O于点D,
∴OD⊥PC,
又∵BC⊥PC,
∴OD‖BC,
∴△POD∽△PBC,
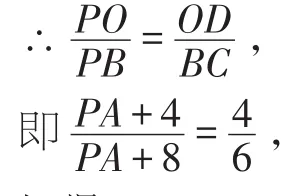
解得:PA=4.
故答案选:A.
【点评】解决数学问题,常常借助条件作为思维的起点.特别是数学中的几何问题,可以采用边阅读边在图上标记条件的方法,并将随之而得的结论写(画)在图形的旁边,再将这些结论进行融合,找到相互间的关联,从而发现解决问题的途径,达到解决问题的目的.
二、挖掘题设中的隐含条件作为思维起点
有些数学问题常常需要挖掘题设中的隐含条件,而圆中的隐含条件往往是一些基本图形.这就需要我们熟悉这些基本图形,将复杂图形转化为几个基本图形的叠加.将这些隐含的基本图形作为思维的起点,可以使题设条件明朗化、具体化,从而达到明晰解题方向、寻求最佳解题方案的目的.
例2如图2,在正方形ABCD中,E是AB上一点,连接DE.过点A作AF⊥DE,垂足为F.⊙O经过点C,D,F,与AD相交于点G.
(1)求证:△AFG∽ △DFC.
(2)若正方形ABCD的边长为4,AE=1,求⊙O的半径.
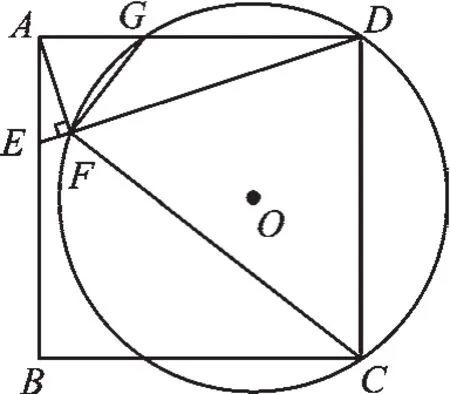
图2
【分析】本题考查了正方形的有关性质、圆内接四边形的性质、三角形相似条件及性质、直角三角形勾股定理的相关知识.第一小题欲证△AFG与△DFC相似.根据圆内接四边形性质及邻补角概念,可得∠AGF=∠DCF,再利用垂直定义、正方形性质、同角的余角相等的相关知识,可得∠GAF=∠CDF,从而第一问得证.第二小题欲求⊙O半径,则可先求⊙O直径,而借助第一问三角形相似及△AED中“母子三角形”相似所得对应边成比例,可得线段AG=AE=1,再由勾股定理求得圆的直径而得半径.有部分同学看不出隐含在题目图形中的基本图形:圆内接四边形及“母子三角形”,导致题设条件不明朗、不具体,不能达到明晰解题方向、快速寻求解题方案的目的.
【解答】证明:(1)因为在正方形ABCD中,∠ADC=90°,
则∠CDF+∠ADF=90°,
∵AF⊥DE,∴∠AFD=90°,
∴∠DAF+∠ADF=90°,
∴∠CDF=∠DAF.
∵四边形GFCD是⊙O的内接四边形,
∴∠FCD+∠DGF=180°,
又∵∠FGA+∠DGF=180°,
∴∠FCD=∠FGA,
∴△AFG∽△DFC.
解:(2)如图3,连接CG.
∵∠EAD=∠AFD=90°.
∠EDA=∠ADF,
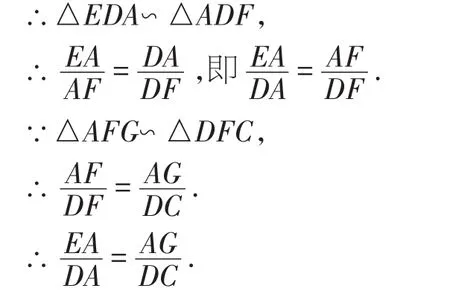
∵在正方形ABCD中,DA=DC,

∴CG是⊙O的直径.


图3
【点评】利用平时数学知识的学习与积累,将一些图形的性质概括与抽象成一些易记的基本图形,并提炼出复杂图形中的基本图形是熟练运用这种方法的关键.迅速地分析出复杂图形中的基本图形,需要平时概括归纳能力的培养.
三、从问题的结论出发,确定思维的起点
初中数学中有些问题的结论不仅是解题的终点,也是解题的起点,调控着解题的全部思维过程.解题中若能恰如其分地用好这些结论的特征,并以此为突破口来确定思维的起点,常常有意想不到的效果.
例3如图4,AB为⊙O的直径,点C在⊙O上,AD⊥CD于点D,且AC平分∠DAB.求证:(1)直线DC是⊙O的切线;(2)AC2=2AD·AO.
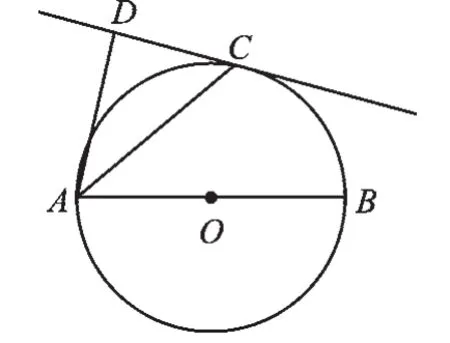
图4
【分析】本题考查了圆的切线的判定方法、相似三角形的判定及性质.
第一小题欲证直线DC是⊙O的切线,仅需连接OC,证明OC垂直于DC即可.
第二小题欲证AC2=2AD·AO,而AB=2AO,则仅需证AC2=AD·AB.将其转化为比例式,再证△ADC∽△ACB即可.
【解答】证明:(1)如图5.连接OC.
∵AD⊥CD于点D,
∴∠ADC=90°,
∵∠ADC+∠DAC+∠ACD=180°,
∴∠DAC+∠ACD=90°,
∵OA=OC,
∴∠OAC=∠OCA,
∵AC平分∠DAB,
∴∠DAC=∠OAC,
∴∠DAC=∠OCA,
∴∠OCA+∠ACD=90°,
即∠OCD=90°,
∴OC⊥CD,
∴直线DC是⊙O的切线.

图5
(2)如图5.连接BC.
∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠ACB=90°=∠ADC,
又∵∠DAC=∠CAB,
∴△ADC∽△ACB,

则AC2=AD·AB,
∵AB=2AO,
∴AC2=AD·2AO=2AD·AO.
【点评】对于第二题中线段等积式结论的证明,我们常常将此结论转化为比例式作为思维的起点;然后对比例式上下(或左右)观察,找出对应三角形进行相似证明;再结合题设条件,确定判定两三角形相似的具体证明方法.这类题目常常会将一些线段的倍分关系掺杂其中,这就需要我们能够根据题设条件将其转换成具体线段.
