积分几何在高职数学教学中的渗透

魏 超

（温州职业技术学院 公共教学部，浙江 温州 325035）

数学是一个有机的整体，内容融会贯通，高层次的数学可看作是对相应低层次的数学内容的推广。“积分几何”作为数学专业研究生阶段的课程，属于高层次的数学内容，许多概念、公式都是对高职数学相关内容的推广，二者有内在的联系，具备渗透教学的条件和基础。高层次数学课程与低层次数学课程的渗透相关研究，已取得一些研究成果[1-4]。

积分几何是通过各种微分、积分变换来研究图形性质的一门学科，本质上属于整体微分几何的范畴，是数学的一个主要研究分支。高职数学的主要内容就是一元函数微积分，某些概念、定理或性质较抽象，不易理解，大多数高职学生只是停留在死记硬背阶段。本文以积分几何中的支持函数、曲率、凸域包含测度为主要对象，结合高职数学中的切线、导数定义、一元函数定积分，在高职数学中进行积分几何渗透教学，可大大提升教学效果。积分几何的思想方法在高职数学教学中发挥着十分重要的作用。

一、积分几何的相关概念

由于高职学生不具备积分几何的知识储备，而积分几何一些相关概念恰恰又是进行渗透教学的基础，如直线的广义法式是假设未知直线方程所取的形式，凸域的支持函数是微分板块中两个研究对象之一，广义支持函数与限弦函数是包含测度公式的重要组成因子。

1.直线的广义法式

直线的广义法式如图1所示。设xOy为二维直角坐标系，OR是自原点引出的射线，由x正半轴到射线OR的角记作φ。G为垂直于OR的任一直线。若G与OR交于点H，规定p（O到H的距离），若O,H两点重合，则p=0；若G与OR的反向延长线交于点H，则规定p=在这样的规定下，直线G的方程为[5]3：

将（1）式称为直线G的广义法式，并记为G(p,φ)；从形式上看，它与直线的一般式一样，但参数p,φ的意义不同。这是积分几何中对直线的表示法，较传统的直线形式有更好的适应性。

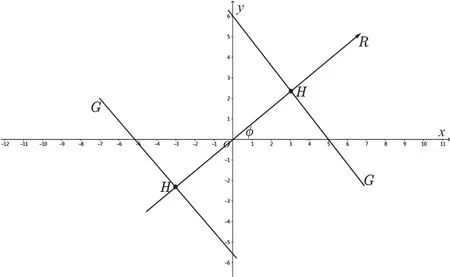
图1 直线的广义法式

定理1直线的广义法式可与直线的一般式相互推导。

证明令直线G的广义法式为xcosφ+ysinφ-p=0，不妨假设p＞0，OR按上述定义，则OR所在直线斜率KOR=tanφ=，此时直线G的斜率KG=-cotφ=G

令G的斜截式为y=-·x+b（*），可得，即b=，将其代入（*）中，有xcosφ+ysinφ-p=0，证毕。

2.凸域的支持函数

设K为欧氏平面E2上的一子集，如果当A∈K,B∈K时，连结A,B的线段也在K内，则称K为凸集。设K为一凸域（即有界闭凸集），在平面内建立二维直角坐标系xOy，自原点O引射线OH，作垂直于OH且与K相交的任一直线G1(p1,φ)（见图2）。集合{p1}的上确界（最小上界）记为p，即：

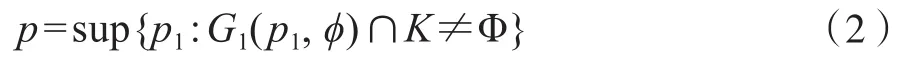
其中，G1(p1,φ)∩K≠Φ表示直线G1(p1,φ)与凸域K有交点，p对应的直线G(p,φ)称为凸域K在φ方向上的支持线。显然，给定一个凸域K，p随着φ的变化而变化，此时可构造函数p(φ)，将其称为凸域K的支持函数[5]4。

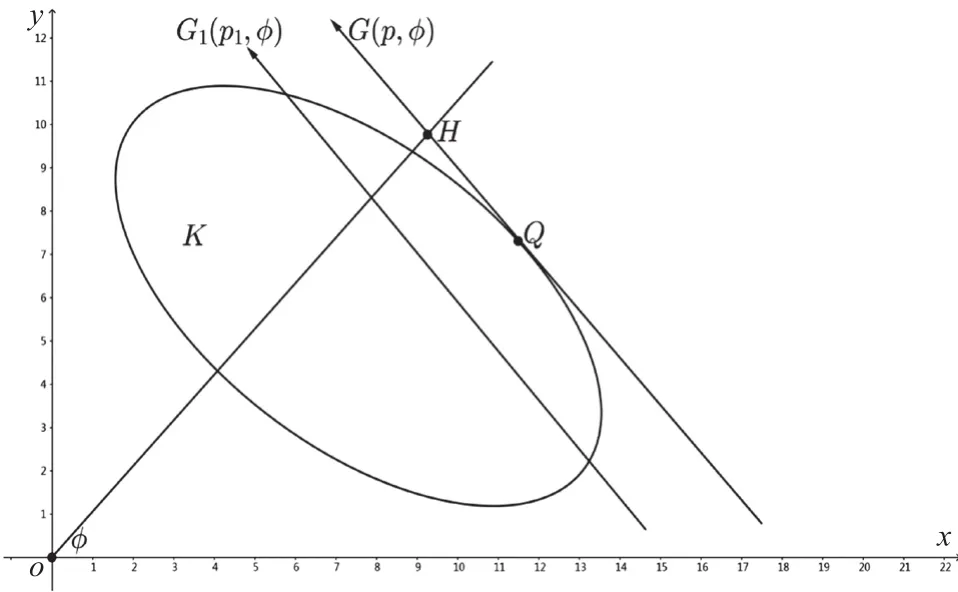
图2 凸域的支持函数

3.广义支持函数与限弦函数

定义1[5]72凸域K被直线G截得的弦长记作σ，∂K表示K的边界，当G仅与∂K相交（包括交集为线段情形），规定σ=0，G取广义法式，对任意给定的σ，φ(0≤φ≤2π)，令

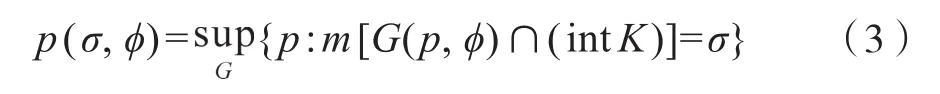
其中m[G(p,φ)∩(intK)]表示G(p,φ)∩(intK)的几何测度，即凸域K被直线G截得的弦长。将二元函数p(σ,φ)称为凸域K的广义支持函数。

定义2[5]72-73用σM(φ)表示垂直于φ方向的直线G与凸域K截得的最大弦长，即：

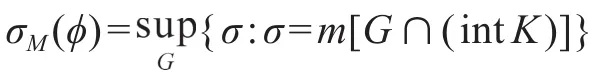
对于任意给定的l(≥0),φ(0≤φ≤2π)，令

称二元函数r(l,φ)为凸域K的限弦函数。

设K为平面上的凸域，周长为L，面积为F，N为长度l的线段，将含于K内的N的包含测度记为m(l)。

定理2[5]73凸域K及m(l)按上述定义。设p(σ,φ)，r(l,φ)分别为K的广义支持函数，限弦函数则有

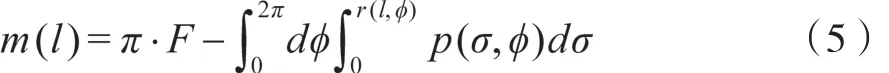
二、高职数学教学中积分几何的渗透

高职数学的内容实际是一元函数的微积分，可分为微分学、积分学两个板块。一方面，积分几何中凸域的支持线从几何角度可看成是对函数图像在某点处切线的推广，积分几何中的曲率就是函数图像上某个点的切线方向角对弧长的转动率，表明曲线偏离直线的程度，二者属于微分学的范畴；另一方面，积分几何中凸域的包含测度是解决积分几何Buffon投针问题的关键，是积分几何学家研究的重要对象，由定理2可知，它归类于积分学。因此，在教学改革实践中，积分几何的渗透可通过在微分教学中渗透某些特殊凸域的支持函数与曲率，以及在积分教学中渗透圆域的包含测度加以实现。

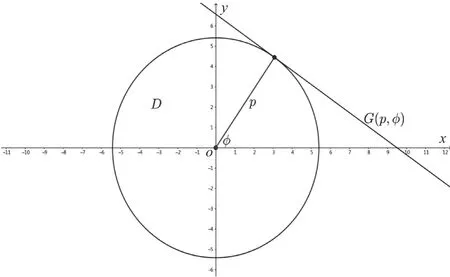
图3 圆域的支持函数

1.积分几何在微分教学中的渗透

（1）凸域的支持函数在导数中的渗透。在讲解导数这一板块时，渗透凸域支持函数，在课堂中列举一些特殊的凸域，让学生尝试利用导数的几何意义求解它们的支持函数，既可帮助学生更好地理解导数及其几何意义，又可拓展学生的几何思维，让学生体会更高层次的几何概念。

函数y=f(x)的导函数为：

其中y=f(x)在x=x0处的导数值记作fφ(x0) ，它的几何意义为y=f(x)的函数曲线在点(x0,f(x0))处的切线斜率。

案例1建立二维直角坐标系xOy，考虑凸域D：x2+y2≤R2（x≥0且y≥0，R＞0为常数）。不妨事先假定 0 ＜φ＜，根据支持函数定义可知，p(φ)={p1:G(p1,φ)∩D≠Ø}。

圆域的支持函数如图3所示。对于任一给定的方向φ，当G(p,φ)∩D为单点集（即G(p,φ)为D的切线）时，p=p(φ)。在点(x,y)处切线斜率为，同时，直线G(p,φ)的斜率为-因而有方程，解之可得 ：x=R·cosφ,y=R·sinφ。G(p,φ)的方程为y=-，利用点到直线距离公式可知，凸域D在φ方向上的支持函数为：

案例2建立二维直角坐标系xOy，考虑凸域：≤1（x≥0且y≥0，a＞b＞0为常数）。不妨事先假定 0 ＜φ＜，根据支持函数的定义可知，p(φ)={p1:G(p1,φ)∩≠Ø}。

椭圆域的支持函数如图4所示。对于任一给定的方向φ，当G(p,φ)∩为单点集（即G(p,φ)为的切线）时，p=p(φ)。在点(x,y)处切线斜率为，同时，直线G(p,φ)的斜率为-，因而有方程，解之可得：，。G(p,φ)的方程为y=，利用点到直线距离公式可知，凸域在φ方向上的支持函数为：

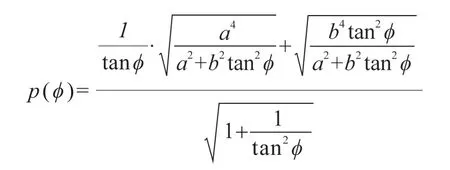
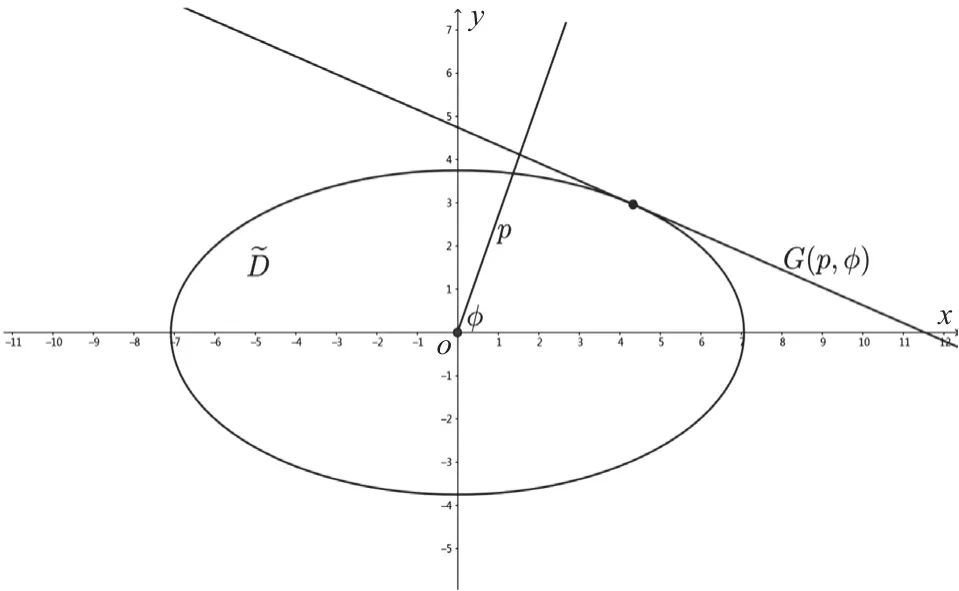
图4 椭圆域的支持函数

案例1、案例2揭示凸域的支持函数与导数的密切关系，渗透凸域的支持函数有助于学生在理解导数几何意义的同时了解相关积分几何概念。

（2）曲率在导数中的渗透。在讲解导数概念时，渗透曲线曲率，汇集一些简单曲线，引导学生探究式地利用导数概念及导数、微分运算找寻它们的曲率表达式，这样可让学生在熟悉导数概念及其运算、微分运算的同时，更深入地理解曲率这一重要几何量，为学生今后更深层次的专门学习奠定基础。

积分几何中曲线的曲率如图5所示。建立二维直角坐标系xOy，平面内任一给定曲线Γ，在Γ上任取两点M,M'，M处切线到M'处切线的角为Δα，沿着Γ曲线MM'的长记为Δs，将称为曲线Γ的曲率，记作κ。

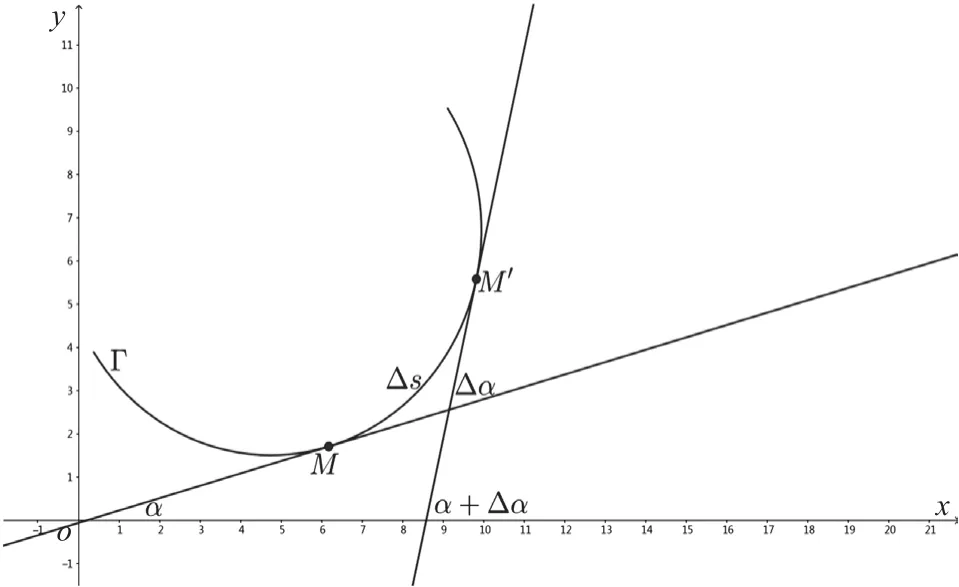
图5 曲线的曲率

案例3考虑圆周曲线x2+y2=R2（R＞0为圆半径）。圆周的曲率如图6所示。在此圆周上任取两点A,B，圆弧AB所对应的圆心角为∠AOB=Δθ，根据弧长公式，可得圆弧AB的长为(Δθ)·R，即Δs=(Δθ)·R，继而另外，圆心角θ和与之对应弧长s的关系式为s=θ·R，亦即，等式两边同时微分，则有这说明圆周是一条常曲率曲线，这一点非常特殊。同时，κ与R的等量关系也让R有了另外一个“名字”——曲率半径。

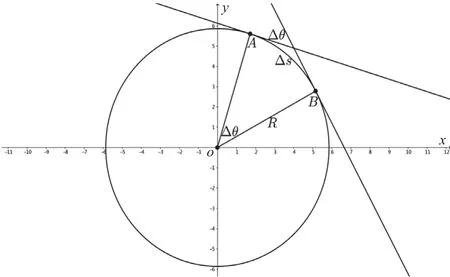
图6 圆周的曲率

案例3揭示曲率与导数、微分之间的紧密联系，渗透曲线的曲率有助于学生熟悉导数的定义及运算，又可让学生初步体会曲率作为最重要的内蕴几何量。

2.积分几何在积分教学中的渗透

在讲解一元函数定积分时，渗透包含测度理论有助于学生更全面地掌握牛顿—莱布尼茨公式及第一、二换元积分法，同时让学生提前接触一些简单的包含测度知识，这对培养学生的几何思维有重要作用。

Buffon投针问题如图7所示。经典的几何概率问题可描述为：假设有2个凸域K0,K1,K1位于K0内部。将长度为l的针N随机地投掷在平面内，现已知N落在K0内部，试求N与K1相遇的概率。这就是所谓的Buffon投针问题。在日常生活中，人们会思考如何将一个篮球准确地投入一个固定容积的框内。数学家则关心一域含于另一域内的可能性，即一域含于另一域内的包含测度，这就归属于积分几何的研究范畴。

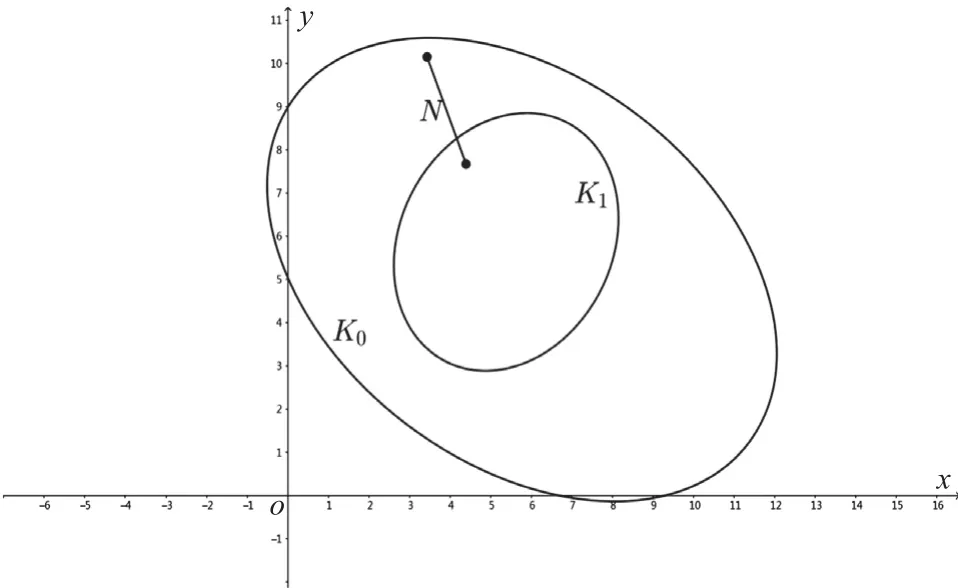
图7 Buffon投针问题

案例4建立二维直角坐标系xOy，考虑圆盘x2+y2≤r2（r ＞ 0 为圆半径）。要求取一长度为l（l ＜ 2r）的线段含于此圆盘内的包含测度m ( l )。

σ(φ)=2r→圆盘的限弦函数r ( l, f)=min{l,MsM(f)}=l。依据定理2得：

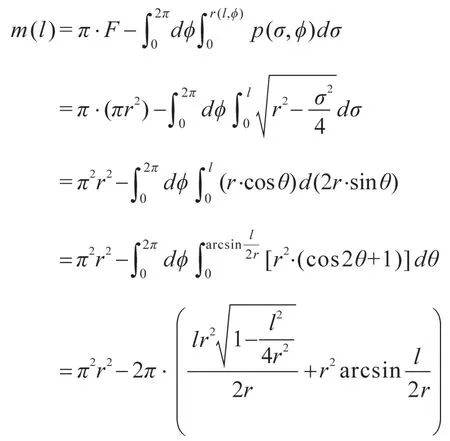
上式即是长度为l（l ＜ 2r）的线段含于圆盘x2+y2≤r2内的包含测度m ( l )。

案例4说明利用一元函数定积分可得到线段含于圆内的包含测度。从计算过程看，求解过程涉及第一、二换元积分和牛顿—莱布尼茨公式，渗透凸域的包含测度可让学生熟悉一元定积分的运算技巧，又可引导学生感知积分几何中包含测度作为最重要的几何量，培养学生的几何素养。

积分几何的思想方法在高职数学教学中发挥着非常重要的作用。积分几何在高职数学教学中的渗透，有利于培养学生的形象思维和学习兴趣，衔接低、高层次数学知识，理解和掌握基本概念和基本思想，提升学生的解题能力，帮助学生树立现代数学特别是几何思维意识。实践证明，高职数学实施积分几何渗透教学，大多数学生表现出更强烈的求知欲，在学习上变被动为主动，学生的学习潜能在一定程度上得以激发，大大提高了教学质量。学生在更轻松地掌握高职数学基本知识的同时培养了学生的几何素养，开拓了学生的视野。