大数据下浙江省公路货运量预测算法的设计与实现

龚大丰，田启明

（温州职业技术学院 信息技术系，浙江 温州 325035）

0引 言

据国家发改委、中国物流与采购联合会的通报显示，2017年全国社会物流总额252.8万亿元，按可比价格计算，同比增长6.7%，增速比上年同期提高0.6个百分点。从分季度看，2017年一季度56.7万亿元，增长7.1%，提高1.1个百分点；上半年118.9万亿元，增长7.1%，提高0.9个百分点，全年社会物流总需求呈现稳中有升的发展态势。[1]随着国家对长三角区域经济发展的重视，浙江省货运规模不断扩大，经济结构、服务模式逐步优化。据浙江省统计局公开发布的数据显示，2007年1月—2018年3月，浙江省铁路货运总量超过37 730万t，公路货运总量超过1 222 347万t，水路货运总量超过723 398万t，同比和环比都有明显增长[2]。这对浙江省交通规划和运输能力等提出了严峻考验。

经济和科技的高速发展，促进了浙江省货运的现代化转型，货运在当今的经济发展中有着重要地位，而货运量的变化，直接反应一个地区的经济状况。运用大数据技术进行管理，做好公路货运量的科学预测，能帮助各地区进行智慧交通管理[3]，也可提高公路货运企业的效益，促进公路货运行业持续、健康和稳定发展[4]，为政府开展更合理的路政管理和服务工作及对当地公路规划和建设具有较强的指导意义。本文运用机器学习算法分析浙江省公路货运量的变化情况，尝试发现其变化规律并做出预测，为相关部门提供参考依据。

1相关算法

由于浙江省公路货运量数据源本身带有所需属性和结果标签值，因而选择监督机器学习算法，结合当前开源且主流的python编程语言和scrapy数据采集框架，实现训练模型的预测功能。目前，国内外货运量预测中通常采用组合模型、无偏灰色预测模型、神经网络、回归曲线模型等多种形式，其中回归模型是一种具体的、行之有效的、实用价值很高的预测途径，因而在货运量预测中常常选用回归模型。通过分析浙江省历年公路货运量数据，可得出它们具有较强的相关性，基本符合回归预测的条件。由于回归预测模型类型较多，致使预测方法不易选择，不同的模型预测结果与实际的差距在精度和可靠性方面都不尽相同。本文对监督机器学习算法中的岭回归算法、朴素贝叶斯算法和KNN算法进行预测分析，对比结果优劣，同时也为分析其他数据提供参考。

1.1 岭回归算法

岭回归，又称脊回归或吉洪诺夫正则化，是对不适定问题进行回归分析时最经常使用的一种正则化方法[5]。岭回归通过对矩阵X'X的对角线上增加一组正常数（即岭参数），降低其病态程度，使得求逆运算相对稳定。如果岭参数的选择合理，岭回归估计的结果会在仅牺牲较小的无偏性下极大地降低参数估计量的方差。因此，从MSE的标准看，岭回归可能优于普通最小二乘估计，即β=(X'X)-1X'Y。在X'X主对角线上增加一个常数后，得到岭回归估计的一般形式为：

其中，k为岭参数，通常k≥0，当k=0时，岭估计即为最小二乘估计，Ip+1为单位矩阵[6]。岭回归是对最小二乘回归的一种补充，它损失了无偏性来换取高的数值稳定性，从而得到较高的计算精度。

1.2 朴素贝叶斯算法

朴素贝叶斯算法是基于贝叶斯定理与特征条件独立假设的分类方法，二者是朴素贝叶斯的两个重要的理论基础。

先验证多项式分布的朴素贝叶斯假设特征的先验概率为多项式分布，多项式朴素贝叶斯是一种生成式模型，可通过（2）式获得，即：

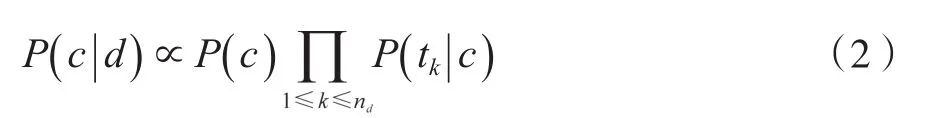
对于朴素贝叶斯算法而言，也就是具有最大后验概率（max-imum a posteriori）估计值的类别，即：

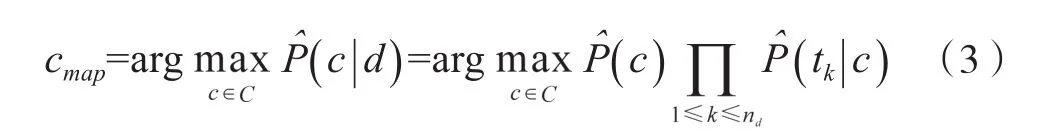
（3）式计算条件概率的乘积，可能会导致浮点数下界溢出，所以引入对数得[7]：

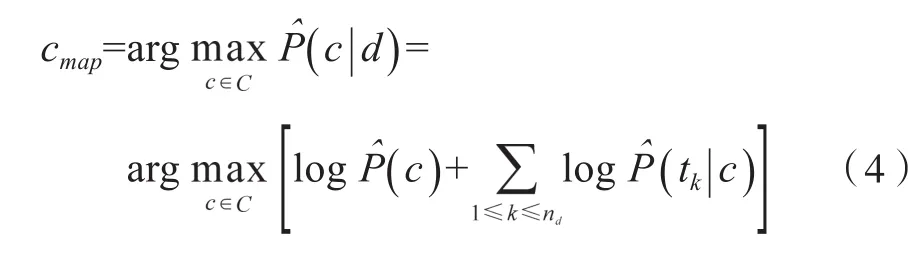
1.3 KNN算法

KNN算法，又称k个近邻分类（k-nearest neighbor classification）算法。它是根据不同特征值之间的距离进行分类的一种简单的机器学习方法，其训练数据都是有标签的数据。KNN算法可用于回归，通过找出一个样本的k个最近邻居，将这些邻居的属性的平均值赋给该样本，就可得到该样本的属性。

KNN算法用于分类的核心思想是：存在一个样本数据集合，又称训练样本集，并且样本集中每个数据都存在标签。输入没有标签的新数据后，将新数据的每个特征与样本集中数据对应的特征进行比较，然后算法提取样本集中特征最相似数据（最近邻）的结果。一般而言，只选择样本数据集中前k个最相似的数据，这就是k近邻算法中k的出处（通常k＜20）[8]。

2浙江省公路货运量预测算法的设计与实现

2.1 数据采集流程设计

为了对浙江省公路货运量进行合理预测，获得一个比较满意的模型供今后参考使用，为数据采集到结果分析的整个实现过程设计如下流程：

（1）通过目前常用的爬虫技术，从浙江省统计局官方网站采集2007年1月—2018年3月所有关于公路的货运数据，部分月份数据不全者进行简单的预处理，保存到本地存储。

（2）以公路货运数据为研究对象，由于所采集数据是当年当月累加值，如3月公布的数据是1月至3月的三个月总量，还需要进一步处理数据，转化为当月货运量。

（3）对预处理后的公路货运数据，按照岭回归算法、朴素贝叶斯算法和KNN算法要求，设计出模型所需的训练集和测试集数据，训练出各模型对应参数，然后用测试集数据进行测试，得出各种算法的准确度。

（4）分析各模型的准确度，选择一种较好的算法作为预测模型。

（5）根据上一步骤的结果，确定公路货运预测算法。

浙江省公路货运量数据采集分析流程如图1所示。

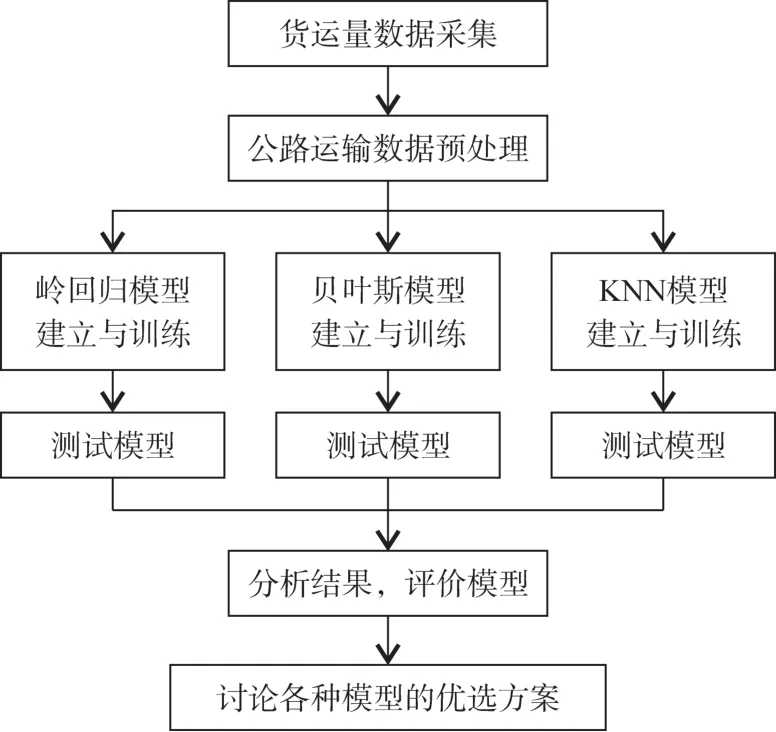
图1 浙江省公路货运量数据采集分析流程

2.2 数据采集

数据采集环节采用当前流行的python环境下的scrapy爬虫框架。scrapy是python开发的一个快速、高层次的屏幕抓取和web抓取框架，用于抓取web站点，并从页面中提取结构化的数据。其步骤如下：

（1）安装scrapy框架，在命令行下，运行pip install scrapy命令即可实现。

（2）创建爬虫项目，在命令行下，执行scrapy startproject zjstatistics，就会在目标目录下创建框架文件，如图2所示。

图2 scrapy项目框架结构

（3）创建爬虫文件spider.py，主要实现对网络请求返回的数据解析，爬取url深度为2，即目录页和货运量数据具体内容页，参考代码如下：

#解析内容函数

def parse（self， response）:

item = ZjstatisticsItem( )

#获得当前Web请求结果，并正则匹配子页链接URL

res = response.selector.xpath（'//tr/td//@href'）

#遍历所有结果

for re in res:

#字符按utf-8解码

suburl = re.extract( ).decode（'utf-8'）

#拼凑成完整的url

item['url'] = suburl[1:]

......

#返回解析结果

yield item

（4）代码调试无误后，运行scrapy crawl zjstatistics命令即可实现数据采集，保存到当前data.csv文件，所采集结果见表1。根据公路货运量数据，将其中的90%数据作为各模型的训练集使用，10%数据作为验证对应模型的准确度进行分析对比。

表1 浙江省公路货运量数据采集结果

2.3 数据预处理

数据预处理的目的是清洗无效数据，将所需数据转化为目标要求格式，为下一步调用算法需要传递的数据集参数做准备。其预处理的主要代码如下：

#读取文件内容

data_str = open（'data.json'， encoding='utf-8'）.read( )

data_list = json.loads（data_str）

data = [[d[' year ']， d[' month ']，d[' highway ']] for d in data_list]

#获得三列数据

src = pd.DataFrame（data， columns=['year'，'month'，’highway’]）

#读取第1、2列为变量集，第3列为结果集

X = src.iloc[:，0:2]

Y = src.iloc[:，2:3]

#随机分配训练集和测试集，由于数据量不够大，按9:1分配

trainx，testx，trainy，testy=train_test_split（X，Y，test_size=0.1，random_state=0）

2.4 基于三种算法的实现

分别采用岭回归算法、朴素贝叶斯算法和KNN算法，实现对公路货运量数据模型的训练。

（1）基于岭回归算法的实现。

#这里指定使用岭回归作为基函数

#定义模型

pp = make_pipeline（PolynomialFeatures（(3)），Ridge( )）

#训练模型

pp.fit（trainx， trainy）

#预测测试集

pp_pred = pp.predict（testx）

#计算符合误差范围的个数，符合一个标准差的值+1

right_num = 0

right_num =（ abs（trainy - pp_pred）＜=err_railway）.sum( )

#计算在误差范围内的准确度

err2=float（right_num） / len（testx）

#打印显示结果

print "PolynomialFeatures accuracy :%f" %（ err2）

（2）基于朴素贝叶斯算法的实现。

#定义贝叶斯模型

clf=MultinomialNB( )

#训练模型并预测测试集

clf_pred = clf.fit（trainx， trainy）.predict（testx）

right_num =( )

#计算符合误差范围的个数，符合一个标准方差的值+1

for i in range（len（clf_pred））:

if abs（trainy.iat[i， 0] - clf_pred[i]） ＜ err_railway:

right_num += 1

#计算在误差范围内的准确度

err3=float（right_num） / len（testx）

print "MultinomialNB accuracy :%f" %（ err3）

（3）基于KNN算法的实现。

#定义Knn模型

knn = neighbors.KNeighborsClassifier( )

#训练模型

knn.fit（trainx， trainy）

#预测测试集

knn_pred = knn.predict（testx）

right_num = 0

#计算符合误差范围的个数，符合一个标准方差的值+1

for i in range（len（knn_pred））:

if abs（trainy.iat[i， 0] - knn_pred[i]） ＜ err_railway:

right_num += 1

#计算在误差范围内的准确度

err4=float（right_num） / len（testx）

print "KNeighborsClassifier accuracy :%f" %（ err4）

2.5 结果比较

利用numpy库可计算出公路货运量数据的标准差为1 932。对公路货运量预测结果和真实值进行比较，在一个标准差的误差范围内，预测的准确度见表2。

表2 浙江省公路货运量准确度

由表2可知，在三种算法中，岭回归算法的预测准确度比较高，为86%；KNN算法的准确度排第二，为84%；朴素贝叶斯算法准确度仅为77%。三种算法在浙江省公路货运量上的误差曲线如图3所示。根据不同算法的测试结果可得出，岭回归算法对浙江省公路货运量预测准确度高，可采用此模型进行预测。

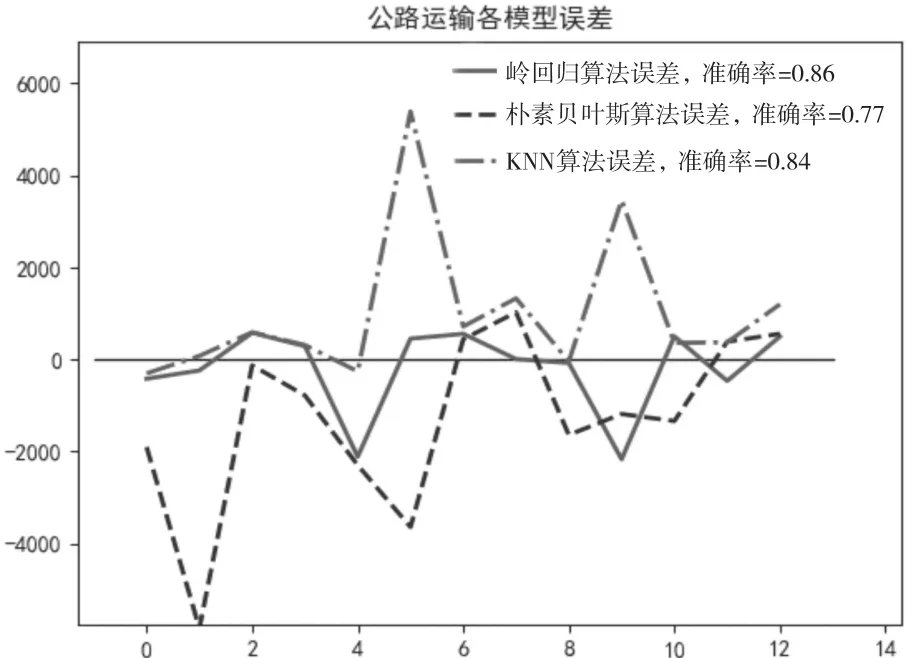
图3 三种算法在浙江省公路货运量上的误差曲线

3结 论

本文结合监督学习算法中的岭回归算法、朴素贝叶斯算法和KNN算法在深度学习领域中的应用，提出一种浙江省公路货运量预测方法。在三种算法中，根据浙江省2007年1月以来的公路货运量数据集的标签集合，选择年份和月份值作为输入变量的特征值，实际公路货运量表示为比较标准值；然后分别利用三种算法作为预测模型，训练样本数据，获得较高的准确度，可在最后的测试集进行准确度验证，利用训练后的模型对将来的某年某月（两个特征值）的公路货运量数据进行预测。岭回归算法在测试集中取得了良好的效果，获得了较好的准确度，表明具有一定的优越性。后续将继续对其他不同算法进行分析讨论，选出更优模型。在此基础上，相关部门应基于大数据平台强化行业辅助决策分析思想，提出整个体系的总体思路、决策体系和实施路径，并进一步加强大数据分析、基础设施规划、货运管理与优化、征信体系建设等方面货运物流大数据的应用。