基于牛顿望远镜系统的激光叠加技术研究

程建高，李 飞，黄智超，王 彦，王克逸

(中国科学技术大学 精密机械与精密仪器系，安徽 合肥 230027)

激光聚焦技术是目前广泛关注的研究方向，在国防[1-3]、空间安全和电力维护等领域有着重要的潜在应用价值。目前，激光光束叠加技术从原理上可以分为相干叠加和非相干叠加[4-6]等2种。由于相干叠加方法需要对光源有严格的相位控制，控制成本较高，因此普遍还是采用非相干叠加方法。目前的激光聚焦系统通常采用的是反射式发射系统[7-8]，这种同轴两镜式的光学结构往往会带来严重的中心遮拦问题。本文通过创新性地改造牛顿望远镜系统的结构，提出并研究了一种激光叠加光学系统，此系统不仅可以解决单支光束能量较弱的问题，也可以有效地避免传统光学系统中常出现的中心遮拦问题，提高了能量的利用率。

1 抛物面成像特点

对于给定焦距f的特定抛物镜，将一点光源放在其焦点处，则入射光束经过抛物镜反射后出射光束为平行光。成像原理如图1所示。

图1 抛物镜成像原理图

不难看出，如果点光源在焦点处有一个微小的偏移，则出射光束会有会聚或者发散的效果。当点光源放置在焦点左侧附近时，则出射光束变为会聚光束(见图2)；当点光源放置在焦点右侧附近时，则出射光束变为发散光束(见图3)。本文提出的非相干叠加系统是基于点光源放置在焦点左侧附近设计实现的。

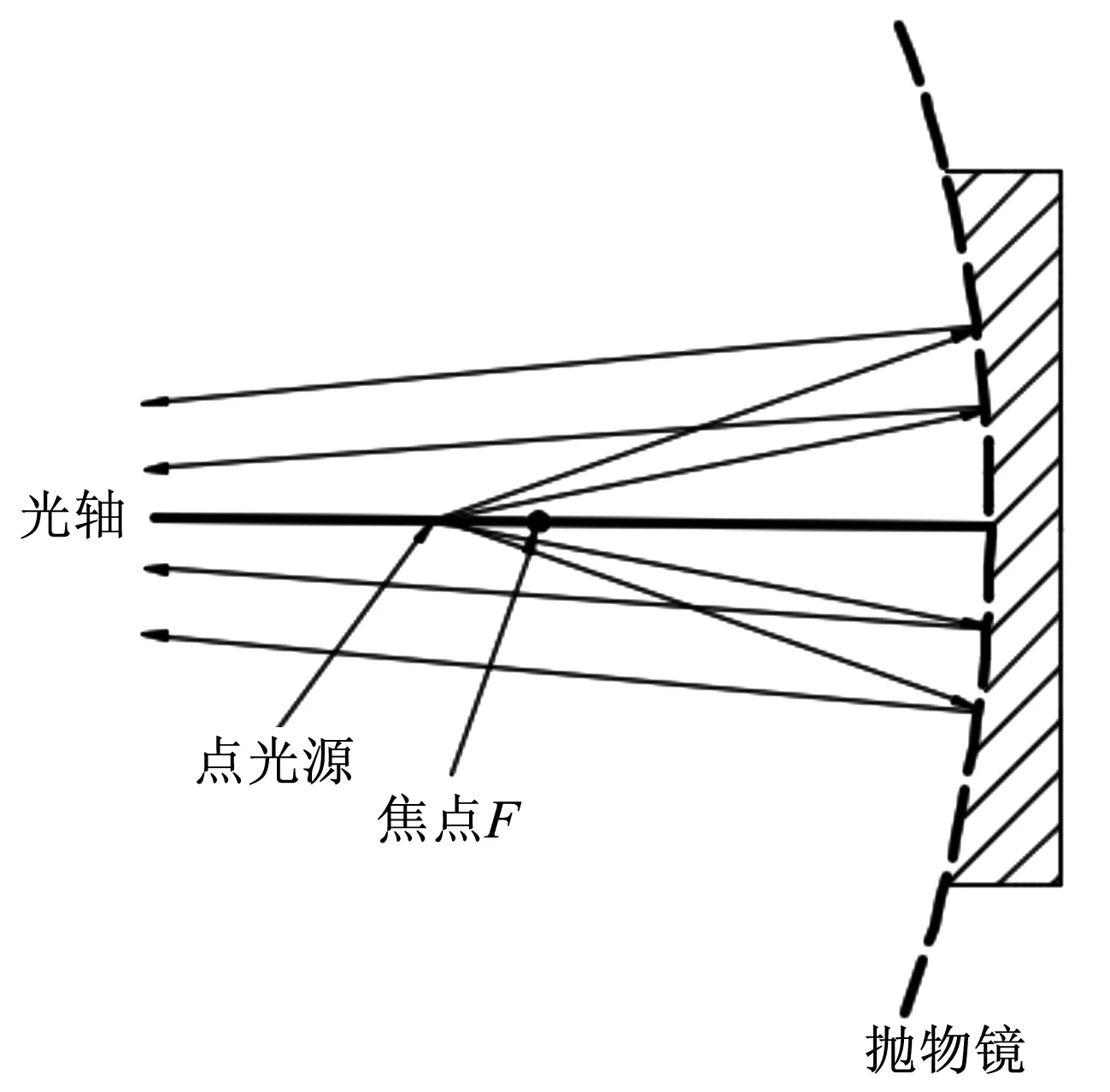
图2 点光源在焦点左侧光路图

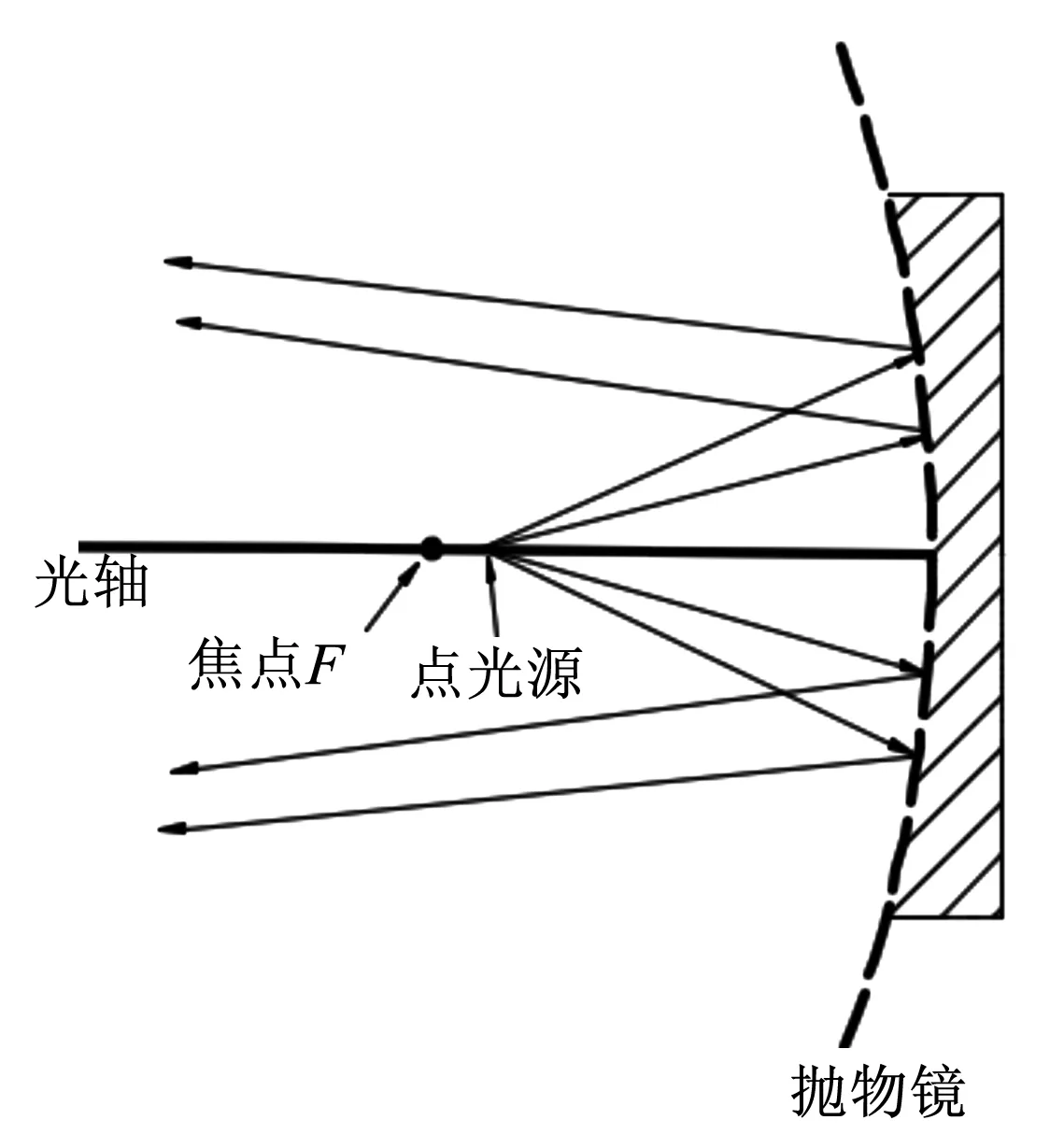
图3 点光源在焦点右侧光路图

2 非相干叠加方案

2.1 叠加原理

本文拟采用空间两两夹角为120°的3片平面反射镜作为各分束的次镜，3束光共用1个主镜，分别打在主镜的3个离轴子孔径上。本文以口径为203.2 mm，焦距为1 016 mm的抛物镜为例进行研究。合束原理图如图4所示，其中点光源和等效点光源关于次镜对称。以主镜半径的中点为离轴子孔径的中心，主镜与离轴子孔径的位置关系示意图如图5所示。由于在变焦过程中离轴子孔径的位置会发生变化，因此子孔径与主镜之间需要预留一定空间。

图4 合束原理图

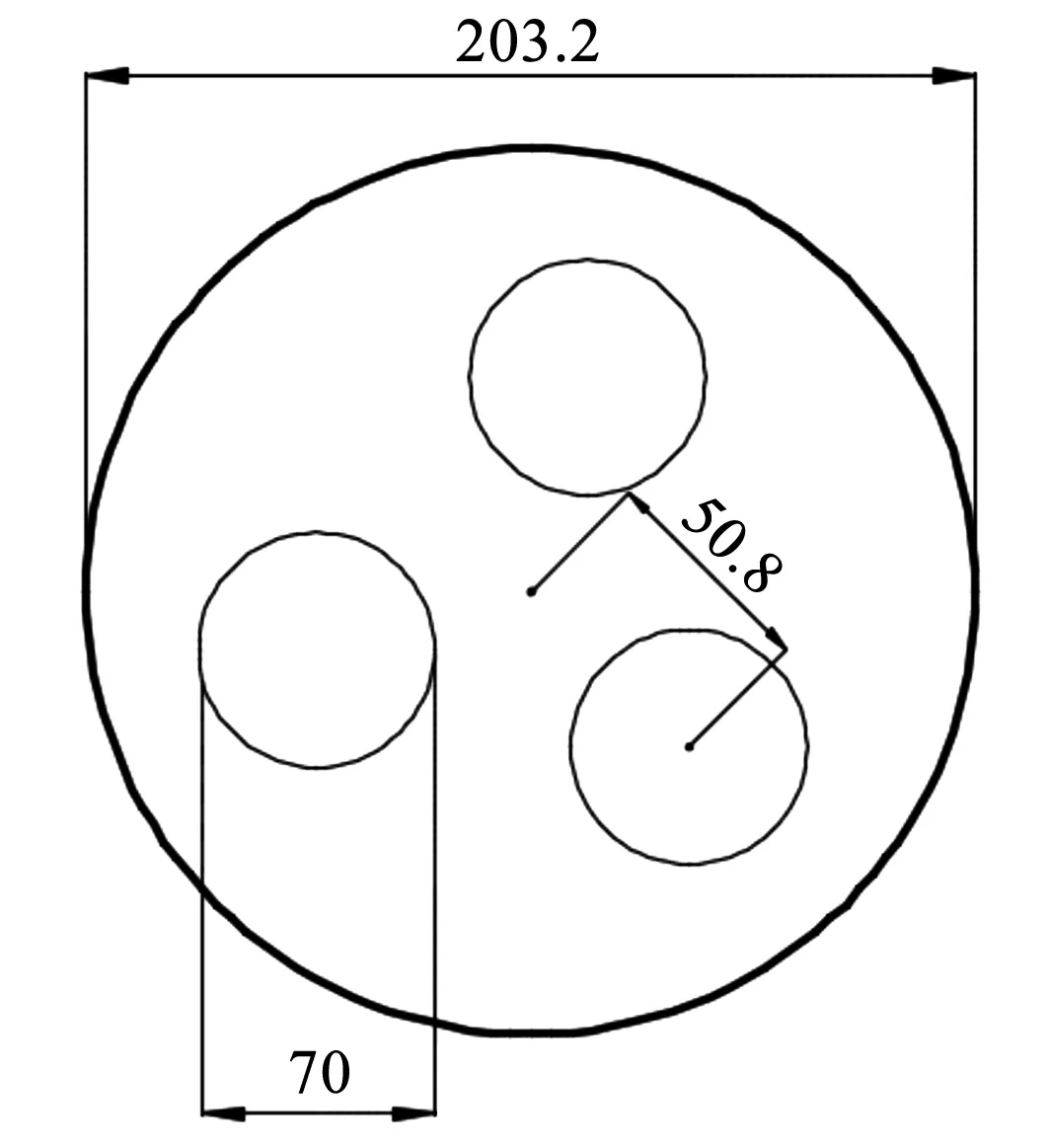
图5 主镜与离轴子孔径位置关系示意图

2.2 结构参数约束关系

设次镜相对于45°反射镜逆时针旋转角度为θ，等效点光源离反射镜中心的距离为L，主镜的离轴量为d。各个参数的约束关系如图6所示。图6中，m为等效点光源到抛物面顶点的距离，n为离轴子孔径中心到抛物面轴线的距离。各参数之间满足如下关系：

n=mtan2θ

(1)

d=Lsin2θ

(2)

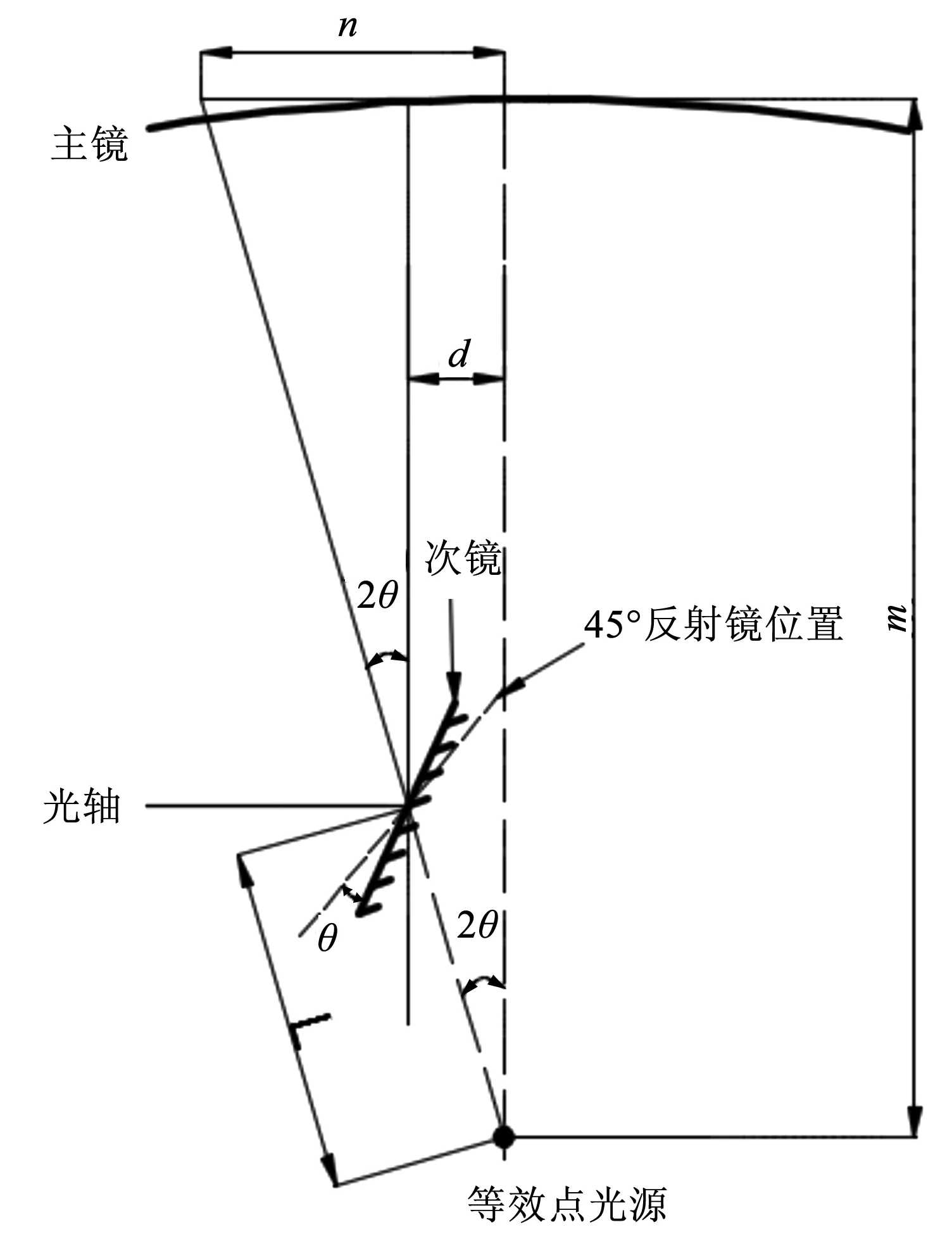
图6 结构参数约束关系示意图

如果将点光源换成平行光束入射，需要在次镜前加一块平凹透镜将平行光发散开。L与平凹透镜参数关系如图7所示。其中，参数lh′说明了主面位置，ld′说明了透镜的位置。由图7中可以得到：

(3)

L=-f′-lh′+ld′

(4)

式中，n为平凹透镜折射率；d为透镜中心厚度。由此，将L与透镜的结构参数联系起来。

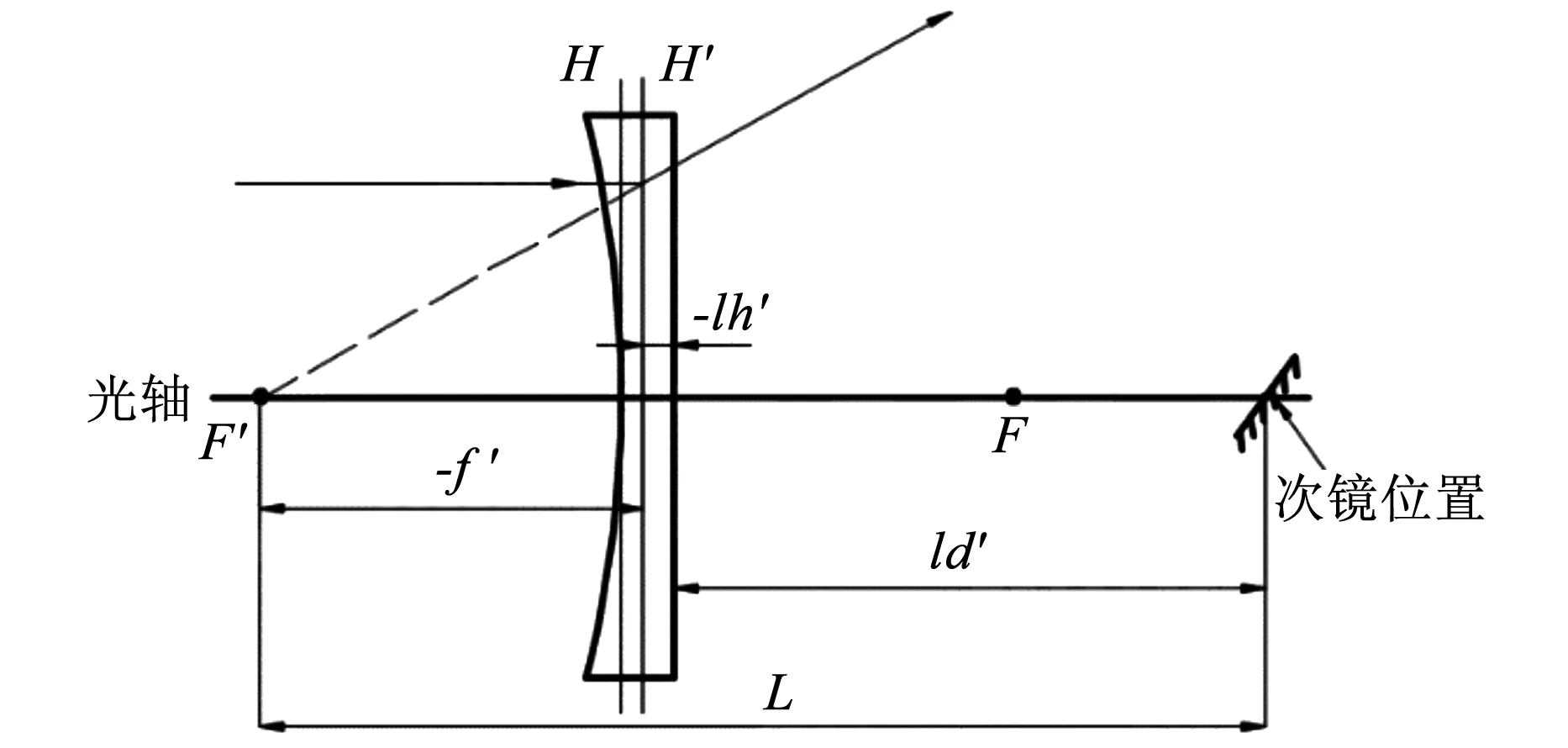
图7 L与平凹透镜参数关系说明图

2.3 中心遮拦解决方法

次镜的存在往往会带来中心遮拦的问题，比如牛顿望远镜。本文提出的光学系统同样也会存在此问题，如果不能合理地解决中心遮拦的问题，对于能量叠加光学系统来说将会损失较大部分的能量。对于本文提出的光学系统，只要保证边缘光线恰好不被次镜遮拦即可。解决中心遮拦问题示意图如图8所示。

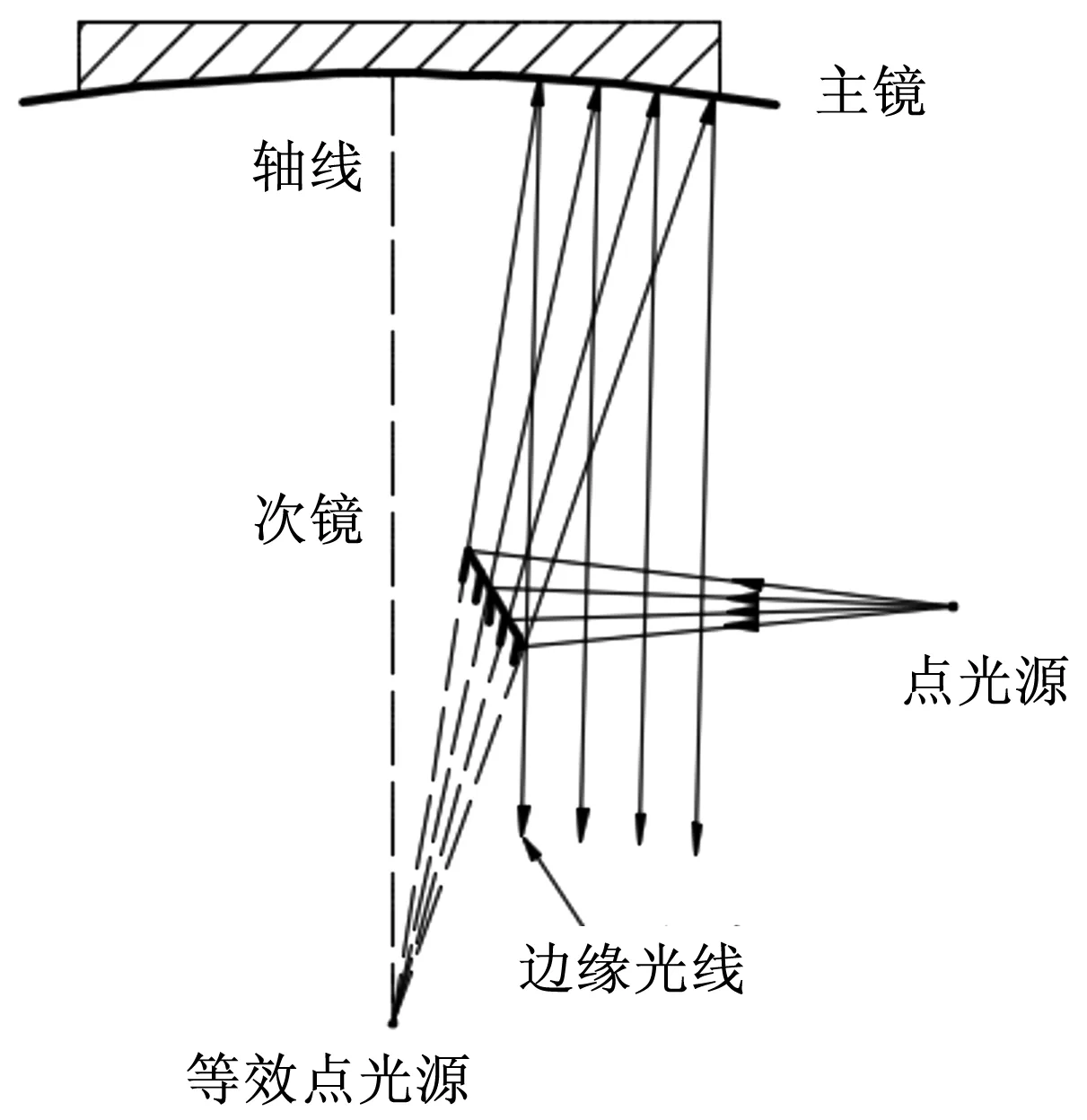
图8 解决中心遮拦问题示意图

需要注意如下2个问题：1)在变焦过程中，点光源的移动应确保其不能进入主镜范围内， 以免对光束造成影响；2)对于本文研究的光学系统来说，当标靶距离、参数n和子孔径的大小确定后，可以得到次镜尺寸的一个最优值(次镜过大会带来中心遮挡，反之会导致能量密度过大)。

3 系统仿真设计

3.1 参数确定

本文以203.2 mm口径抛物镜，标靶距离2 km为例进行设计仿真。将抛物镜的结构参数输入到Zemax镜头编辑器中，将2 km处的光斑大小作为优化目标，点光源到抛物镜顶点的距离m设置为变量。经过程序优化得到m的最优值为1 016.516 4 mm。由本文事先确定的参数n及子孔径的大小，可以通过MATLAB编写程序确定其他各参数的值：L=193.777 3 mm，d=9.671 9 mm，θ=1.430 5°。考虑到中心遮拦和次镜上能量密度问题，可以得到次镜的半径最优值R=9.512 8 mm。

3.2 Zemax光学建模

通过Zemax，设置光学系统波长为1 080 nm，视场为0°，入瞳直径为6 mm。3支分光束的非相干叠加只是各分支光束能量的简单相加，因此，在建立模型时只需要考虑单支光束即可。

3.2.1 点光源入射

点光源入射时，通过Zemax建立模型，得到系统各光学表面的参数见表1。此光学系统的点列图如图9所示。均方根半径为81.052 μm。3支分光束同时入射时生成的点列图是3个两两夹角为120°的点列图的叠加。

表1 ZEMAX中各光学表面参数

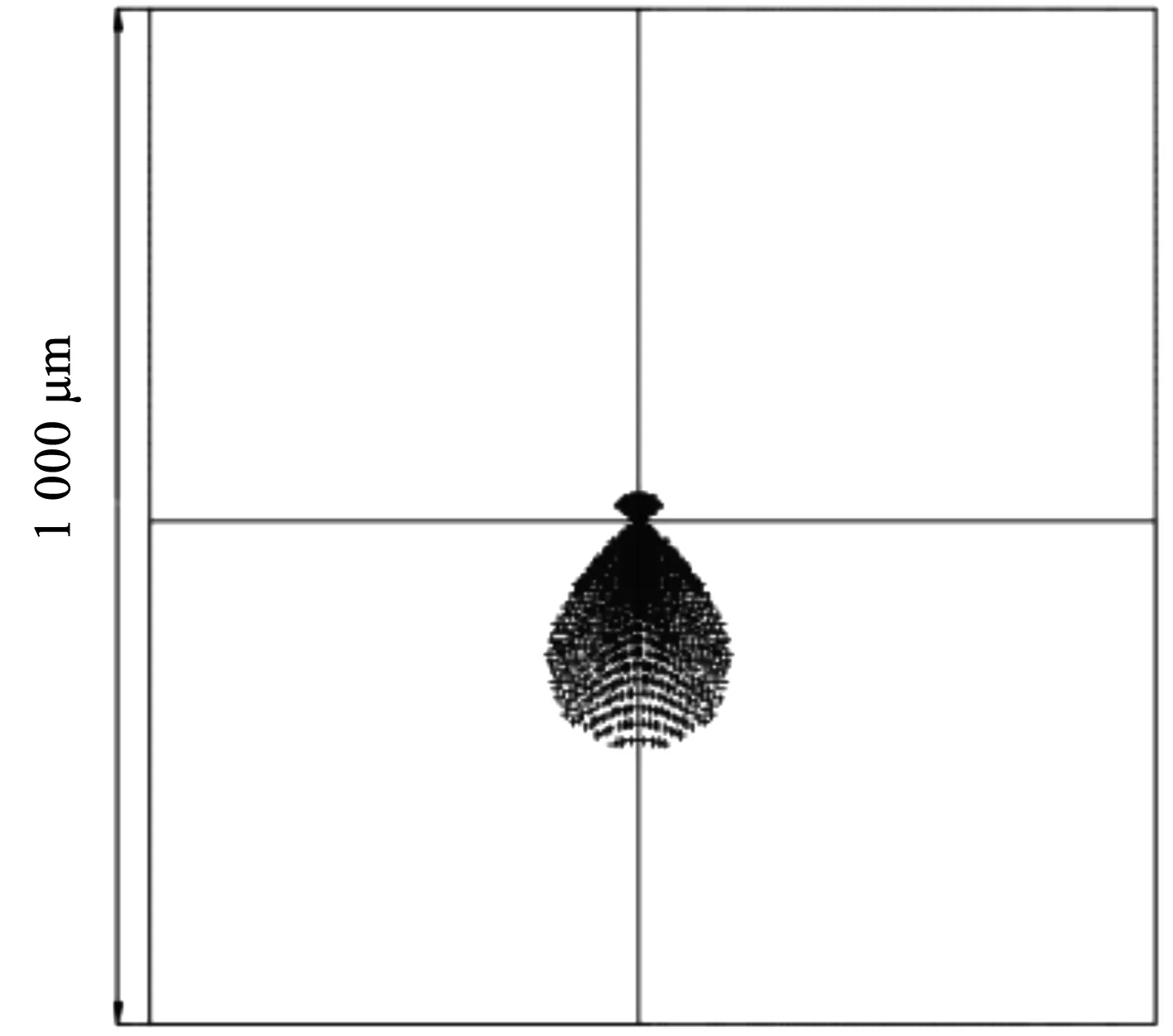
图9 点光源入射时系统点列图

3.2.2 平行光入射

如上所述，当在次镜前加入一块平凹透镜时，就可以将点光源换成平行光束，二者是等效的，只需保证平凹透镜的前焦点在点光源位置处即可。此时光学系统中各表面参数见表2。此光学系统的点列图如图10所示。均方根半径为3.105 mm。

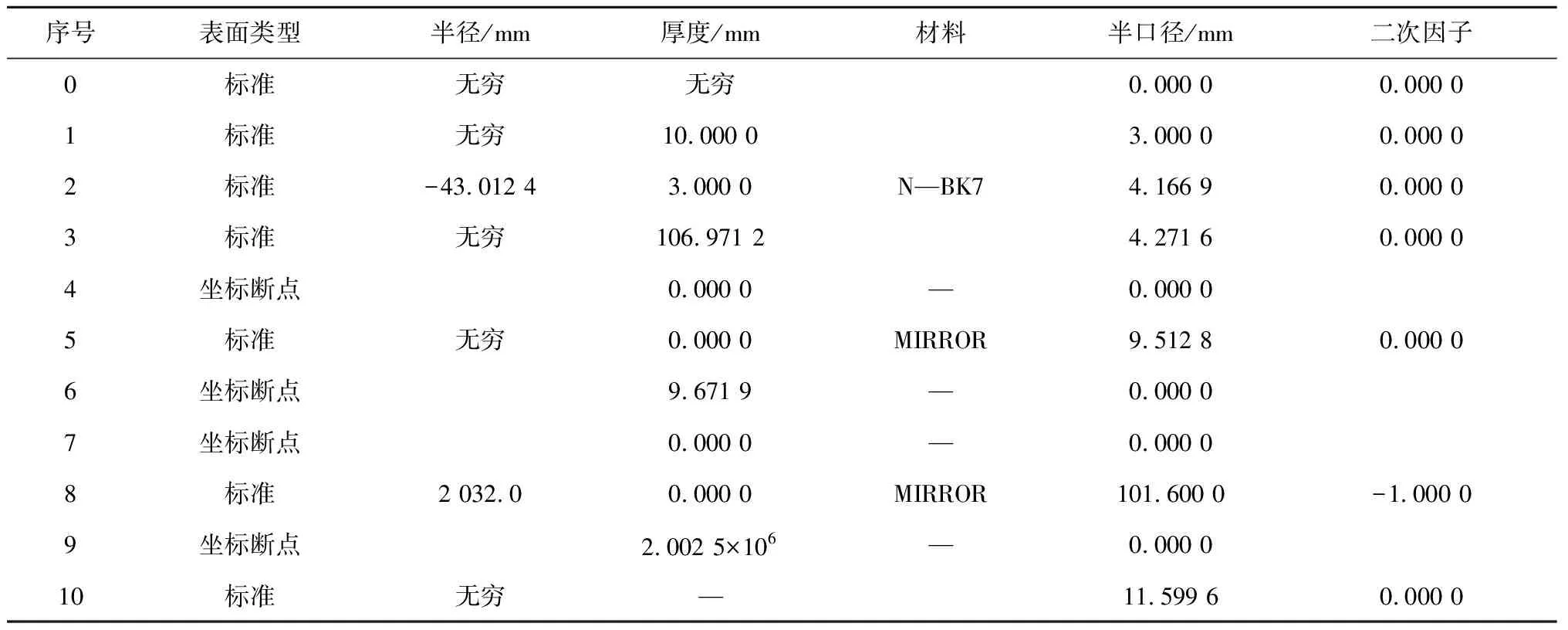
表2 ZEMAX中各光学表面参数

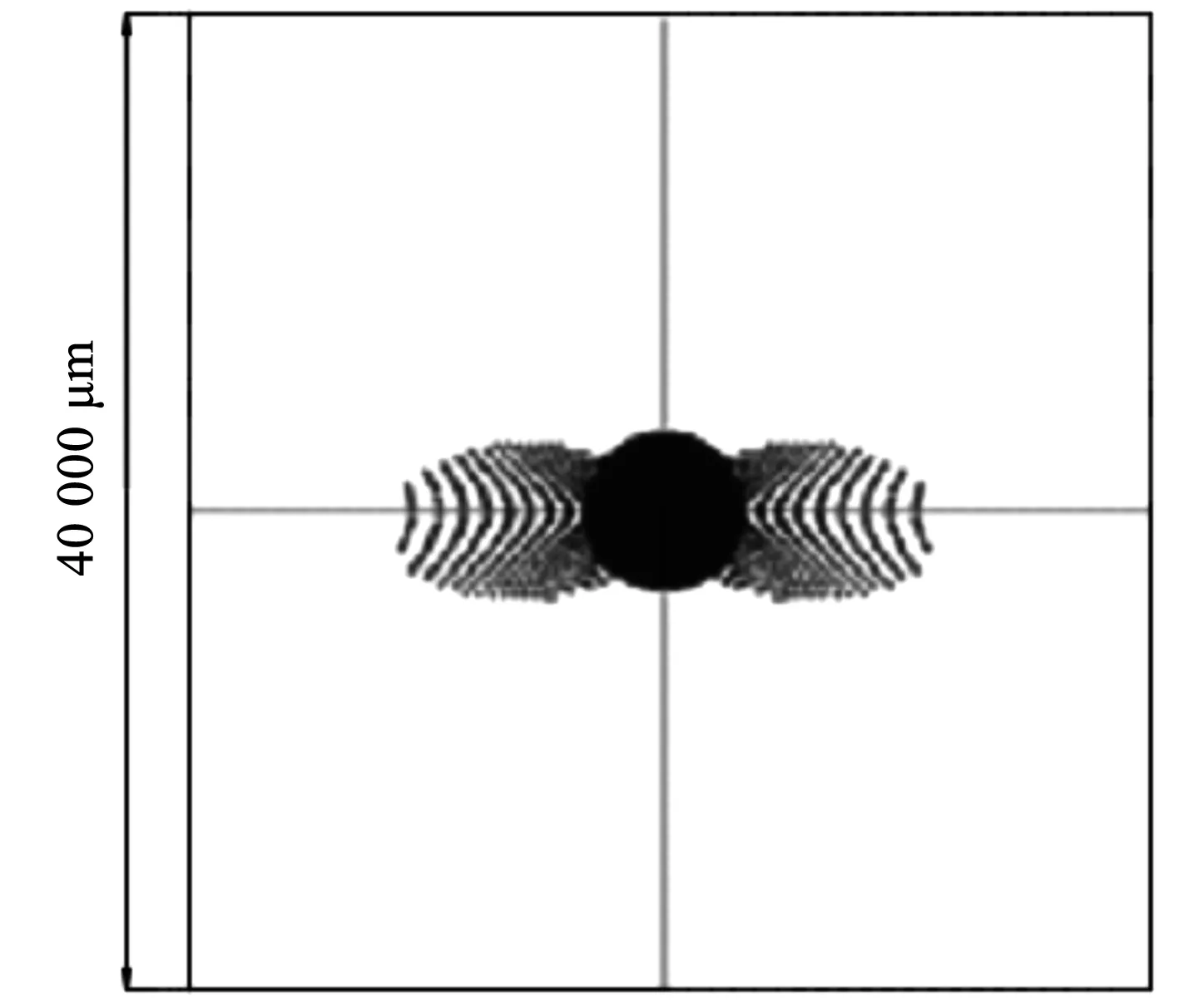
图10 平行光入射时系统点列图

3.2.3 高斯光束入射

高斯光束[9]在其光束横截面上的光强分布为高斯分布。将入射的平行光换作高斯光束入射，高斯光束波长为1 080 nm，束腰为3 mm。通过追迹光瞳内的部分光线得到在像面上的坐标位置。应用MATLAB软件绘制当入射光为高斯光束时像面的光强分布(见图11和图12)。对比点光源、平行光和高斯光束入射情况下的光斑图，由于单光束的光路结构是关于y-z平面对称的，因此得到的光斑图都是关于z轴对称的。由Zemax得到点光源入射和平行光入射时像面上x方向和z方向上的能量分布图(见图13)。其中,纵坐标已经归一化。由图11和图13可以看出，3种情况下像面上的能量主要集中在半径为3 mm的圆内，聚焦效果显著。

图11 光强三维分布图

图12 光强二维分布图

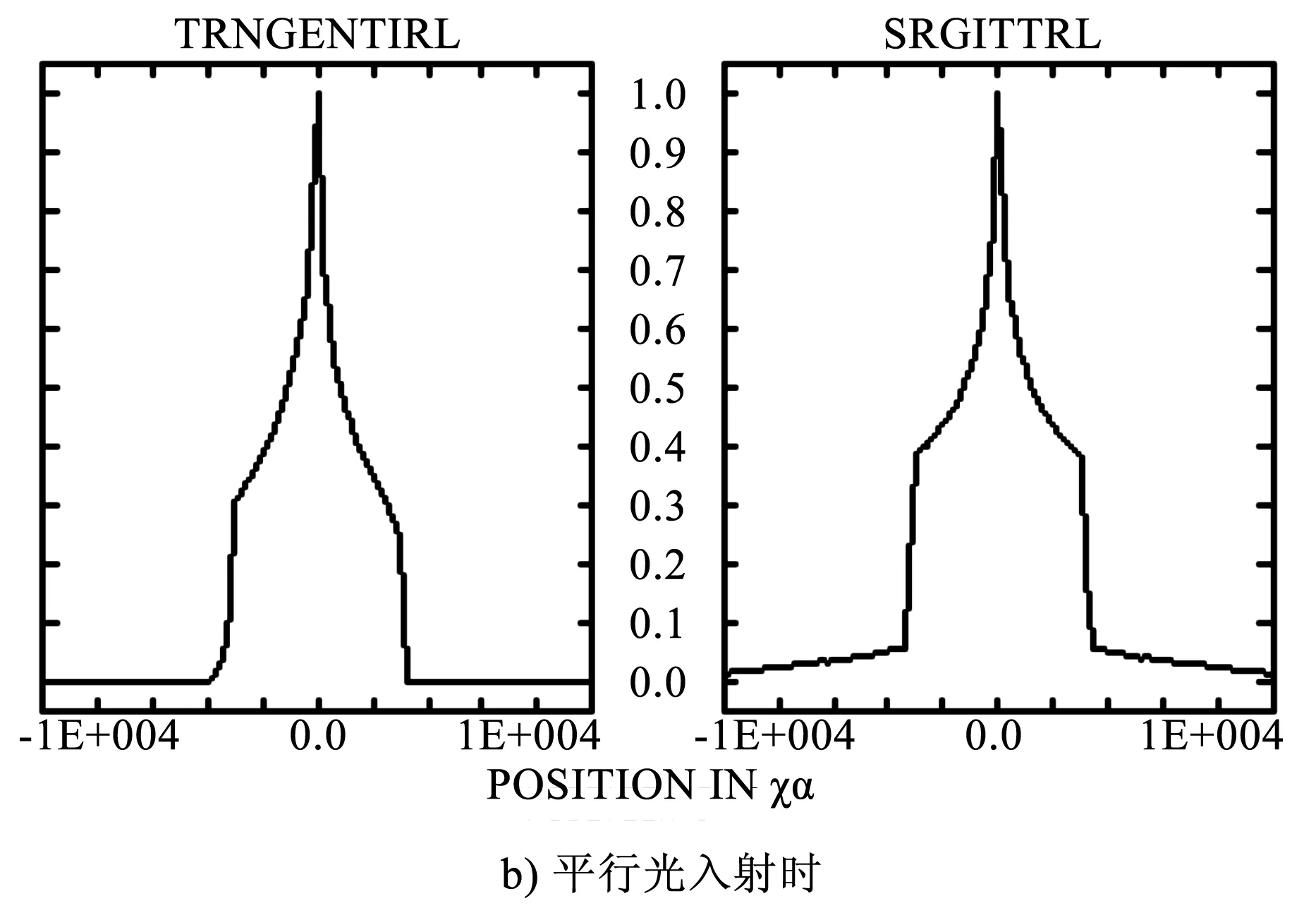
图13 像面能量分布图

4 变焦设计

根据上文知道，只要适当改变等效点光源到抛物镜顶点的距离m的大小，即可实现变焦效果[10]。对于三光束光强叠加系统，由于光源位置限制，改变标靶位置时，等效点光源的移动需要同时改变次镜角度和激光光束变换透镜的位置，以保证光束聚焦在主镜光轴上。变焦设计说明图如图14所示。已知变焦前的系统参数L、θ和变焦后等效点光源位移量Δx，由图14给出的几何关系，可计算出次镜旋转的角度Δθ和变焦后的系统等效点光源到次镜的距离L′，即：

(5)

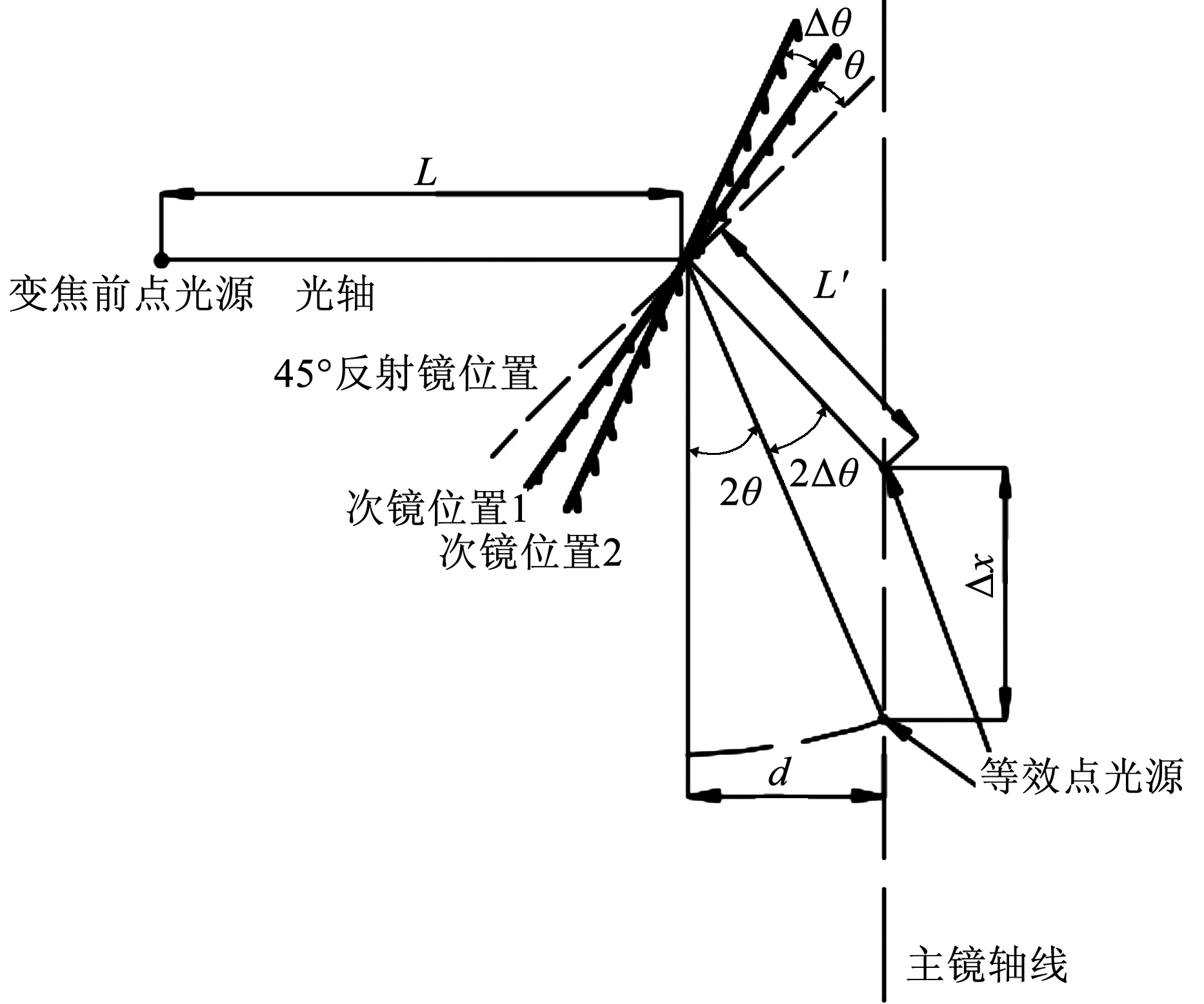
图14 变焦设计说明图

可见，可以通过调节平凹透镜的轴向位移和次镜的旋转角度来实现变焦。通过Zemax仿真可以得到不同聚焦距离时m的变化范围(见图15)，聚焦距离取1～2 km。

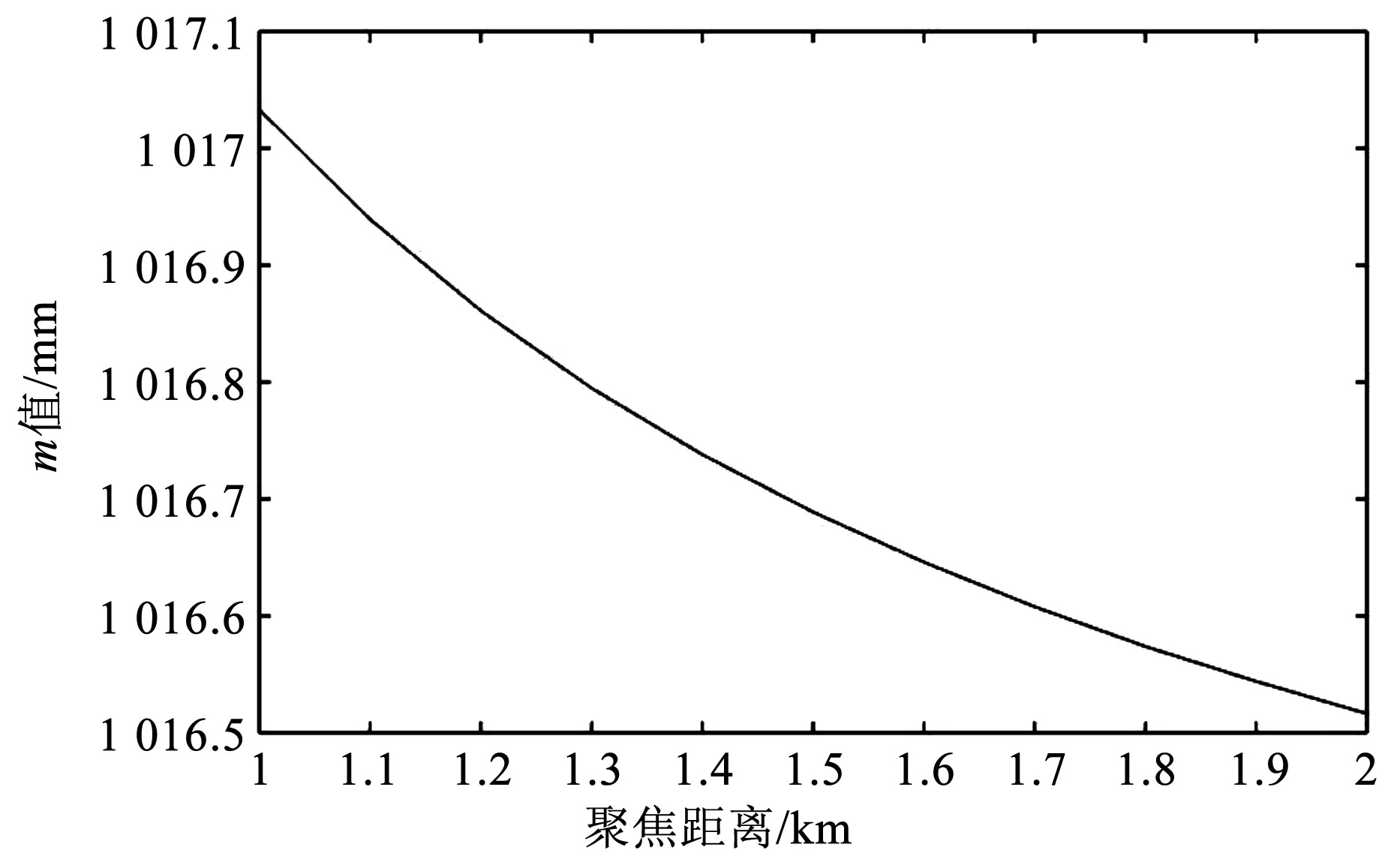
图15 m值与聚焦距离变化关系图

实际上通过调节平凹透镜的轴向位移量和次镜的旋转角度来调节m值的大小。表3列出了不同聚焦距离相关结构参数的变化量。相对于2 km聚焦距离次镜位置，假设顺时针旋转时Δθ符号为正，平凹透镜远离次镜时ΔL符号为正，由表3给出在1～2 km聚焦距离范围内，等效点光源的位移量Δx与平凹透镜的位移量ΔL的变化量。次镜的旋转角度变化量非常小，需要精密调控。

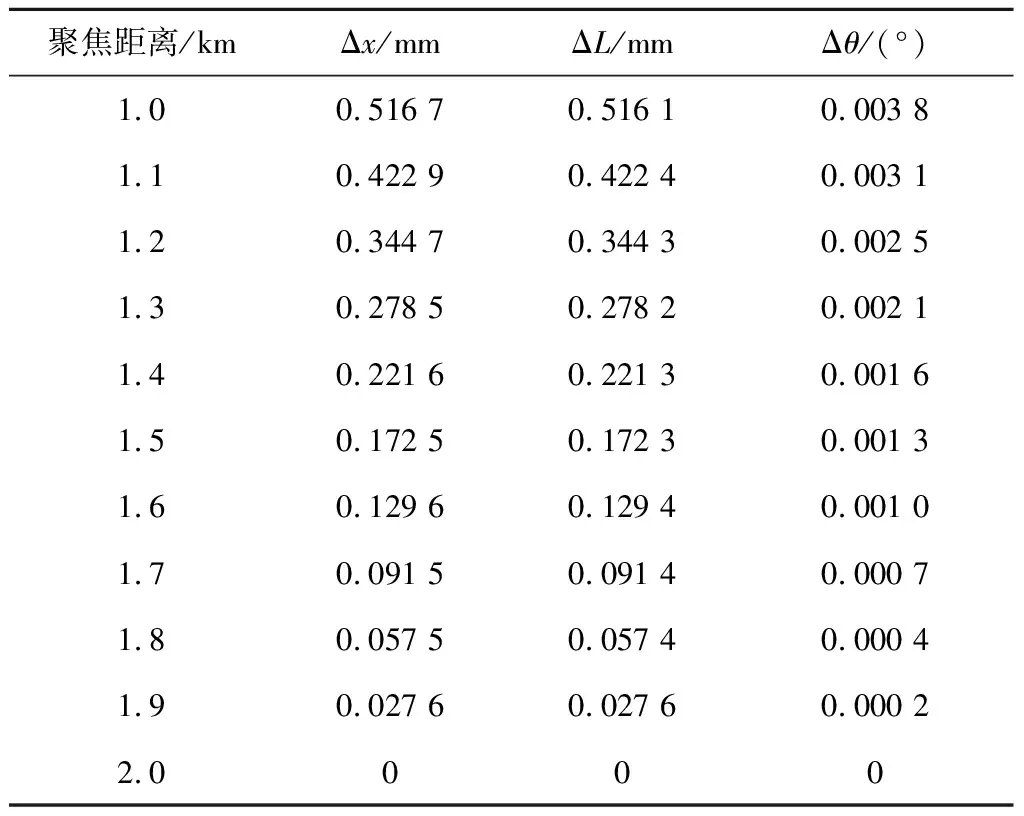
表3 不同聚焦距离光学器件位置变化量

5 结语

本文基于牛顿望远镜系统提出并研究了激光聚焦时的非相干叠加方法，具体内容如下：1)针对抛物镜的成像特点提出了非相干叠加光学系统，3束激光各自经过平凹透镜和次镜后，打在主镜上形成3个离轴子孔径，经过反射在目标距离处聚焦；2)给出避免中心遮拦的几何参数关系，通过追迹边缘光线，可优化次镜位置和入射光束位置，确保反射光束不被次镜遮挡；3)通过Zemax光学建模，给出了单支光束入射时的系统点列图，对比点光源、平行光和高斯光束入射时的光斑图；4)针对1～2 km的聚焦范围，提出变焦方法。仿真结果表明，本文提出的激光非相干叠加方法可以为具体的工程试验提供理论支持。