方波曲线耦合零交叉边缘检测的图像加密算法
2018-10-24卢世军张福泉
朱 珍,卢世军,张福泉
(1.广东工程职业技术学院 信息工程学院,广东 广州 510520;2.中山大学 地理科学与规划学院,广东 广州 510275;3.北京理工大学 软件学院,北京 100081)
0 引 言
当前较为主流的图像加密技术主要分类为[1-9]光学加密与混沌加密。如Chen等[5]提出基于多干涉光束与矢量分解的光学图像加密方案,利用相应的光学加密结构与装置,完成图像加密。曾大奎等[6]提出了基于两步正交相移干涉的光学图像加密算法,设计光学加密装置与路径,结合双随机相位编码,完成数字图像加密。Zhao等[7]设计了改进的相位检索技术的光学图像加密机制,有效破坏了明文与密文之间的线性关系。虽然此类光学技术具有多密钥维度和高速并行处理的优点[7]。然而,光学加密技术是将明文信息完全保留在一个POMS中,易导致密文产生轮廓问题,降低了密文的安全性。
近年来,混沌加密技术被广泛研究,如孙倩等[8]设计了基于改进cat映射与混沌系统的彩色图像快速加密算法,采用比特置乱技术与改进的cat映射来完成图像加密。Li等[9]提出了基于改进的Tent映射的图像加密算法,利用改进的Tent映射与扩散机制,对明文进行加密。Chai等[10]提出了基于混沌系统与DNA序列的图像加密技术,利用DNA编码技术与波形置乱技术,改变DNA矩阵中每个元素的位置,建立逐行扩散机制,对置乱的DNA矩阵完成扩散。
混沌加密技术[1]可避免光学加密存在的轮廓显示等不足,但是低维混沌映射的安全性不佳,而高维混沌映射的加密效率较低[9],且当前混沌图像加密技术存在一个共同的缺点:在置乱与扩散过程中,都是将相同的加密操作应用于所有的明文像素,导致算法的随机性不高。
为了解决上述难题,充分利用置乱与扩散的双重加密结构优势,本文设计了基于方波空间填充曲线与零交叉边缘检测的选择性图像加密算法。该加密技术是一种混合域加密算法。首先,引入正交多项式变换OPT,借助零交叉边缘检测机制,在OPT时域中确定图像的感兴趣区域与非重要区域。通过设计一种方波空间填充机制,对感兴趣区域与不重要区域进行置乱,输出置乱子块。随后,利用明文像素值,定义两个引擎参数,设计异扩散函数,利用相应的扩散函数对感兴趣区域、不重要区域进行独立加密,借助可逆OPT机制,得到其对应的扩散结果。最后,测了所提加密算法的安全性与抗攻击能力。
1 本文选择性图像加密算法
所提的基于方波空间填充曲线与零交叉边缘检测的选择性图像加密算法过程如图1所示。其主要包括3个阶段:①感兴趣区域与非重要区域的划分;②基于方波空间填充机制的明文置乱;③基于异扩散函数的图像加密。
1.1 感兴趣区域与非重要区域的划分
令初始明文为f(x,y),其尺寸为N×N,为了快速分析图像的时域特征,本文引入正交多项式变换OPT技术[11]。根据OPT原理[11],其对应的点扩散函数M(x,y)可被视为实值函数。基于M(x,y),则明文f(x,y)二维OPT变换为
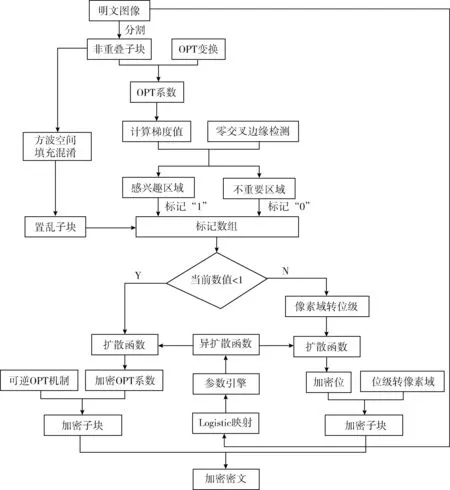
图1 本文选择性图像加密算法过程
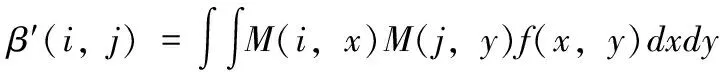
(1)
式中:β′为OPT系数。
根据OPT技术,将式(1)演变为矩阵形式
(2)
(3)
其中,⊗为外积运算;|M|为OPT的点扩散算子;u(x)为其正交基。
依据式(2)与式(3),即可得到输入图像的OPT系数,从而将图像从空域转变为时域,详细的OPT变换见文献[11]。
随后,引入零交叉边缘检测机制[12],在OPT时域中找出符合人眼视觉的边缘。其步骤如下:

(2)根据两个相邻的OPT系数,计算每个3×3子块的梯度值
(4)
(3)设置判断阈值T;
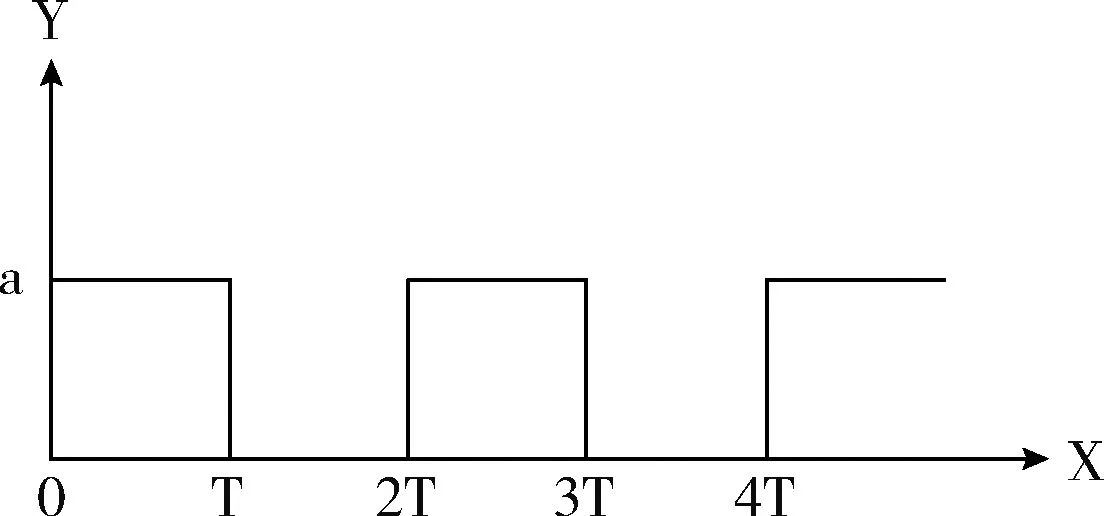
(4)若梯度值D (5)计算梯度值D的二阶偏导D″ (5) 若D″<0,则在此子块的中心标记边缘点,同时统计该子块的边缘点数量,用cnt表示。利用上述过程处理所有的子块,完成整个图像的边缘点标记。 (6)再设置阈值T2,其最小值为0,最大值为100。 (7)若子块中的边缘点数量cnt>T2,则该子块被视为感兴趣子块;否则,为非重要子块。将感兴趣子块标记为1,非重要子块标记为0,将这些标记值组合为一个数组; (8)若某个子块为感兴趣子块,则利用可逆OPT机制处理这个子块的系数,得到空域值。 (9)执行上述过程,直到最后一个子块,整个过程结束。 空间填充曲线[13]是一种连续遍历图像所有像素的混淆方法,能够提高图像像素位置的置乱度。胡亦等[14]提出了一种锯齿填充曲线来实现图像的像素混淆,取得了良好的效果。本文基于文献[14]的思想,通过改变曲线形状,提出了一种空间填充曲线,称为方波空间填充曲线。图2展示了一种方波的多种表示。其中,a为曲线高度;T为宽度。所提的方波填充曲线可精确地在每个方向穿过每个像素,有效避免置乱周期性。不同模式的方波曲线如图3所示。其中,图3(a)~图3(e)为初始模式;图3(f)为图3(e)的拓展模式;k为方波曲线穿过的图像像素数量。依图可知,所提方波空间填充曲线不受明文尺寸的限制,不仅可以对方形图像进行混淆,还能对非方形图像进行置乱,具有良好的通用性。本文就是利用这种方波空间填充曲线在空域上完成像素置乱。 图2 方波 图3 不同模式及其拓展版的方波空间填充曲线 为了研究不同k值的方波空间填充曲线的置乱效果,本文以图4(a)为例,利用k=1、3、8、12、16、30对应的拓展曲线对其进行混淆,结果如图4(b)~图4(g)所示。依图可知,随着k值的增大,图像的置乱效果更好,如图4(b)~图4(e)所示;但是,当k继续增大时,其置乱效果反而降低,如图4(f)~4(g)所示。 为了体现所提方波空间填充曲线的优势,将传统的锯齿填空曲线[14]、Zigzag扫描以及Raser曲线视为对照组,利用频谱失真来量化置乱效果,结果见表1。由表可知,随着k值的增大,置乱密文的安全性越高,当k大于12时,其性能逐步降低;另外,与其它3种技术相比,所提算法的置乱效果最好,其频谱失真均要大于对照组。这表明置乱图像与明文是截然不同的,充分掩盖了明文信息。 图4 不同k值下的方波空间填充曲线的置乱效果 表1 不同空间填充曲线的置乱效果 图像经过上述置乱后,虽然其像素位置得到了充分混淆,但是每个像素的像素值却没有变,使其安全性不理想[15]。为此,本文利用明文自身像素,基于Logistic映射[1]来设计异扩散机制,对感兴趣子块、非重要子块进行差异化加密。Logistic映射具有结构简单,加密效率高等特点,其函数为[1] xk+1=λxk(1-xk) (6) 式中:λ∈[0,4]是混沌控制参数;xk为系统变量。 为了改善所提技术的抗明文攻击能力,借助初始图像的像素来获取式(6)中的x0 x0=T/107 (7) 式中:T为明文的像素总数。 然后,利用如下的量化机制对{x1,x2,…,xM×N}进行处理,获取一组加密密钥{ki} ki=mod(floor(xi×1014), 256) (8) 再利用明文像素值,定义两个引擎参数kt1,kt2 (9) (10) 利用kt1,kt2,设计异扩散函数,对感兴趣子块、非重要子块进行独立加密 S′(i)ROI=S(i)⊕k(i)⊕S(kt1)⊕S(kt2) (11) S′(i)N-ROI=S(i)⊕k(i)⊕S(kt1) (12) 对于感兴趣子块、非重要子块,分别利用式(11)、式(12)对其相应的OPT系数进行扩散。通过3×3的逆OPT变换,得到相应的扩散子块,从而完成图像加密。 借助式(11)、式(12)对图4(e)实施加密,结果如图5所示。依图5(a)可知,输出图像的内容被高度隐秘,经过异扩散后,输出一幅与置乱图像截然不同的密文,呈现类似噪声干扰结果;且扩散密文的像素分布较为均匀,如图5(b)所示。这表明该机制具备较高的安全性。 图5 图像加密结果 为了验证本文加密技术的有效性与优异性,在MATLAB软件中进行测试,并将文献[8]、文献[9]视为对照组。实验环境为:Intel3.5 GHz、双核CPU、4 GB的内存;系统是Window 7。关键参数设置为:子块尺寸为3×3,判断阈值T=35[16],λ=3.6,方波空间填充曲线的a=8,W=8,且其穿越像素数量k=12;另外,经过多次加密实验,取阈值T2为60。 以大小为480×480的明文为实验目标,如图6(a)所示,并采用本文方法、文献[8]、文献[9]对其实施加密,输出结果如图6(b)~图6(d)所示。依图可知,明文被本文方法与对照组技术进行置乱-扩散后,其信息被高度隐蔽,没有任何信息泄露,外来攻击者无法从中得到任何有用的线索。但是,主观评价难以区分三者技术的差异,为此,本文引入信息熵值[2]来客观量化这三者的加密安全性,测试数据见表2。依据表中的测试数据,所提机制、文献[8]和文献[9]算法的保密能力都很好,且本文技术的熵值最大,约为7.9994;而文献[8]、文献[9]输出的密文熵值分别为7.9978、7.9953。原因是所提技术设计了方波填充曲线,通过一次遍历所有图像像素,充分提高了像素置乱度,且无置乱周期性,同时,依据人眼视觉特性,将整个图像分割为感兴趣区域与非重要区域,利用初始明文的像素来设计异扩散函数,对感兴趣像素与非重要像素进行独立差异加密,显著破坏了加密算法的线性关系,增强了算法的随机性,该算法从空域与时域两个方面完成像素加密,显著提高了密文的安全性。而文献[8]则是采用比特替代传统的字节来完成图像像素的置乱,通过动态改变每一轮的加密控制参数,并借助改进的二维Cat映射来输出一组密钥流,对图像进行扩散,具有很高的加密安全性,但是此技术在像素的置乱与扩散过程中,均是采用了相同的加密操作,虽然其采用了动态加密原理,但这种扩散机制仍然存在一定的线性关系,易被攻击者利用,使其安全性要略低于所提技术。文献[9]则是利用一维Tent映射来实现图像的快速加密,但是一维Tent映射结构较为简单,其混沌行为不理想,且在图像加密过程中,借助同一加密机制对明文实施混淆,使得此技术仍存在线性关系。 图6 不同加密算法的输出密文 表2 各算法对应的密文熵值测试 图像像素之间通常具有较高的相关性,攻击者可以利用这特性来破译密文,对算法的安全性影响较大[4],一般而言,图像中的像素分布不均,出现堆积现象,则显示其相关性越强烈,其安全性越低,反之,则其相关性较小,安全性越高。对此,本文测试了文献[8]、文献[9]以及所提加密技术的密文相关性。从图6(a)~图6(d)中随机选择2000对相邻像素来计算其相关系数Cxy[4] (13) 不同算法的Cxy计算数据如图7所示。由图7(a)可得,明文的其像素分布极为不均,所有像素堆积为对角线形态,这说明其像素间的相关性非常高,其Cxy值为0.9583;然而,经过本文算法、文献[8]、文献[9]置乱与扩散后,图像的像素分布变为均匀状态,这种对角线形态的得到了极大改善,Cxy分别为0.0011、0.0026、0.0043。通过对比图7(b)~图7(d)可知,所提技术的输出密文的像素分布均匀度最高,无像素堆积现象,要优于文献[8]、文献[9]的加密机制。 图7 不同算法的密文像素相关性测试 剩余两个方向的Cxy结果见表3。由表可知,对于3个方向,初始图像的Cxy值始终是最高的,表明其相关性是最高的。但是,明文被所提方法、文献[8]与文献[9]加密后,其相关性被显著降低,Cxy值出现了大幅下降,同样,在这三者中,所提加密机制的Cxy值均为最小。 表3 3个方向的相关系数测试结果 图像在网络中传输时,面临的最大威胁就是明文攻击,主要分为两类:已知明文攻击与选择明文攻击[17]。因此,良好的加密技术应能有效抵御此类攻击,为了量化这3种不同加密方法的抗明文攻击能力,本文引入NPCR与UACI值[4]评估加密机制的抗选择明文攻击能力 (14) (15) (16) 其中,W,H分别是图像的高度与宽度;I,I′分别为2个明文被加密后输出对应的密文,且这两个明文都只存在一个相异灰度值。 本文将图6(a)作为测试对象,把像素点(105,39)的像素值112改为19,再借助所提技术、文献[8]、文献[9]对修改前后的图像进行加密,并基于式(14)~式(16),形成了NPCR、UACI曲线,如图8所示。可见,所提机制的抗选择明文攻击性能最佳,对应的NPCR和UACI值均为最大,分别是99.86%、35.23%,而文献[8]、文献[9]算法的NPCR、UACI值都要小于所提机制。原因是所提加密方法的扩散阶段是与明文自身像素密切相关,使得不同的明文会产生不同的密钥,导致攻击者无法对算法进行破译,另外,利用初始明文的像素来设计异扩散函数,对感兴趣像素与非重要像素进行独立差异加密,显著破坏了加密算法的线性关系。而文献[8]、文献[9]算法都没有考虑初始图像的特性,使得加密密文与明文特性无关,导致其抗选择明文攻击能力不理想。 已知明文攻击主要借助攻击来获取算法的解密密钥,从而用于其它密文的复原[17]。为了量化这3种加密技术的抗已知明文攻击性能,基于文献[17]的方法,对本文算法、文献[8]、文献[9]进行了测试。以图9(a)为已知明文,利用本文算法、文献[8]、文献[9]各自对应的算法对其加密,输出的密文如图9(b)~图9(d)所示,此时,攻击者已经获取了这些密文。再利用文献[17]的攻击方法对这些密文进行破译,得到了相应的解密密钥。通过这些密钥,对图6(b)~图6(d)完成解密,结果如图9(e)~图9(g)所示。依据解密结果可知,所提加密技术的抗已知明文攻击能力最高,攻击者利用其获取的密钥是无法对图6(b)进行正确解密;而文献[8]、文献[9]算法的抗已知明文攻击能力不理想,其对应的密文均被不同程度的解密,泄露了图像的部分信息,如图9(f)、图9(g)所示。 图8 3种算法的抗选择明文攻击能力来量化测试 本文测试了密钥λ=3.6的敏感性,其余密钥保持不变。通过利用微小因子δ=10-16来改变密钥λ,获取两个错误密钥:λ1=3.6+10-16、λ2=3.6-10-16,从而形成3组密钥,一组是正确的,其余两组为错误。再利用这3组密钥对图5(a)进行解密,结果如图10(a)~图10(c)所示,并测试了λ=3.6相应的MSE曲线,如图10(d)所示。依图可知,利用两组错误密钥对其进行解密,是无法获得正确的明文图像,如图10(a)~图10(b)所示;只有利用正确密钥λ=3.6方可对其完成解密,输出正确的明文,如图10(c)所示。另外,由图10(d)可知,λ=3.6具有理想的“雪崩效应”,当密钥无变化时,其MSE曲线发生了剧烈变化。这说明本文算法具有理想的密钥敏感性,能够很好地满足“雪崩效应”。 为了提高加密算法的安全性与抗明文攻击能力,本文设计了基于方波空间填充曲线与零交叉边缘检测的选择性图像加密算法,从空域与时域上完成像素的置乱与扩散。通过设计一种方波空间填充曲线,对明文子块进行置乱,高度混淆像素位置;同时,引入正交多项式变换OPT(orthogonal olynomials transform),对每个明文子块进行OPT处理,获取每个子块对应的OPT系数,以计算每个子块梯度值;基于零交叉边缘检测机制,联合梯度值与用户阈值,判断子块的重要性,将其划分为感兴趣区域与不重要区域;并利用明文像素值来设计异扩散函数,对明文的不同区域进行选择性加密。实验结果表明了所提算法的有效性与优异性。 图10 本文算法的密钥敏感性测试1.2 基于方波空间填充机制的明文置乱



1.3 基于异扩散函数的图像加密
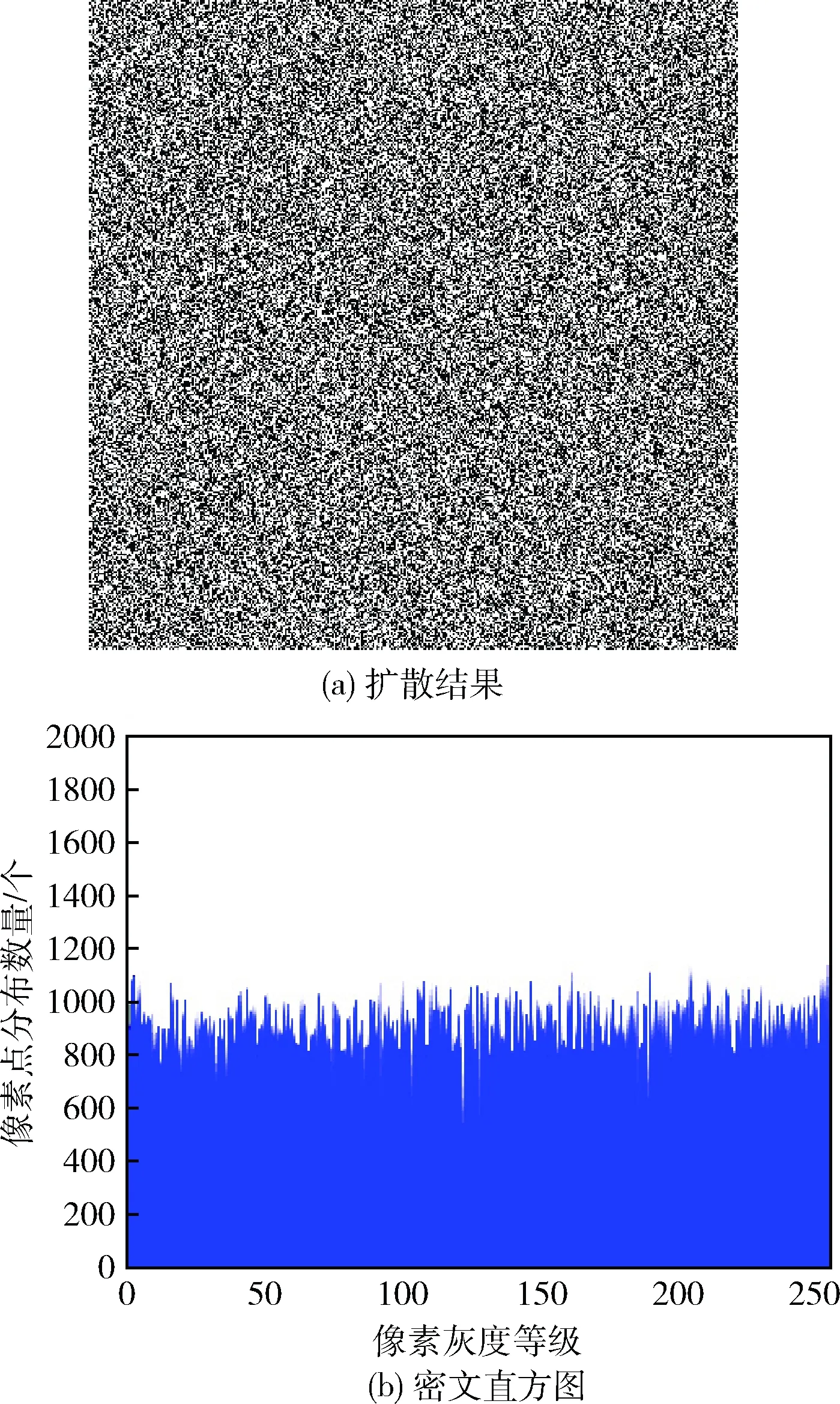
2 实验结果与分析
2.1 加密效果分析


2.2 密文相关性分析
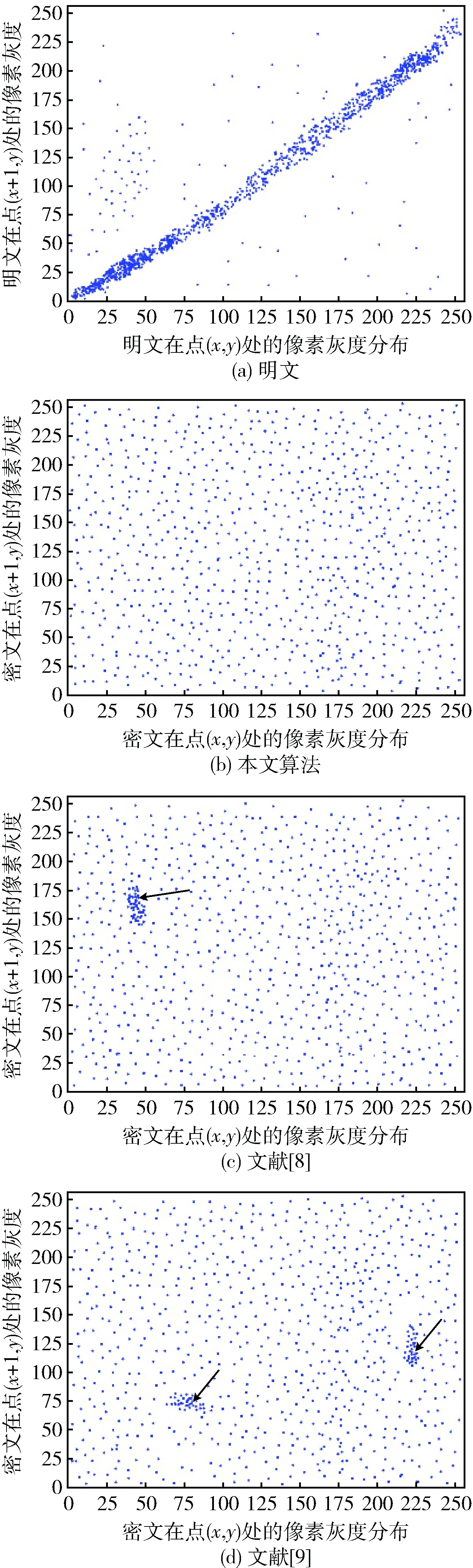

2.3 抗明文攻击能力测试


2.4 密钥敏感性测试
3 结束语

