用类比、分类、转化“唱响”轴对称

姜鸿雁（特级教师）

众所周知，初中阶段共学习三大基本图形变换，分别是平移、翻折（轴对称）、旋转.翻折是继平移后的第二大图形变换，如何学好这部分内容呢？本文从以下三个方面与同学们聊聊，相信你们定有收获！

一、从类比的角度学习

回忆图形平移的知识框架：

类比平移，感受轴对称（图形）学习路径：

在类比旧知识的过程中学习新内容，有利于形成整体观，会使学习过程更轻松.

二、用分类的视角思考

本章图形因轴对称的特殊性，使符合题意的图形相关元素之间的数量关系相对复杂，位置关系也常不确定，用分类讨论的视角思考，是确保解题结果不重复、不遗漏的“法宝”.

【例1】如图1，线段AB与直线l相交于点A，在直线l上确定点C，使△ABC是等腰三角形（画出所有符合题意的点C）.

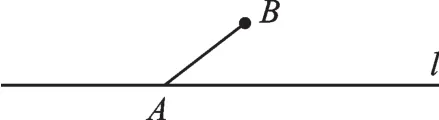
图1

图2

【分析】等腰三角形只有两个顶点确定，则腰和底边均无法确定，故要分类讨论.科学的分类依据是确保结果不重复、不遗漏的关键.本题研究对象是等腰三角形的顶点，分类依据考虑顶角顶点为上策.当点A为顶角顶点时，则有AB=AC，以点A为圆心、AB长为半径的圆与直线l的交点即为点C；同理，当点B为顶角顶点时，以点B为圆心、BA长为半径的圆与直线l的交点即为点C；当点C为顶角顶点时，线段AB的垂直平分线与直线l的交点即为点C.所以符合题意的点C共有四个（如图2）.为便于理解与记忆，可以把图2简称为“两圆一线”，为日后解决更为复杂的与等腰三角形相关的问题做好铺垫.

三、以转化的思想求解

化难为易、化陌生为熟悉……这些都是转化思想的魅力，是解决问题的有力保障.由于轴对称（图形）、等腰（边）三角形的各条性质，注定本章与全等三角形有紧密联系，这在解决问题过程中，为转化线段或角提供了“资源”.用好这些“资源”，可以轻松解决问题.

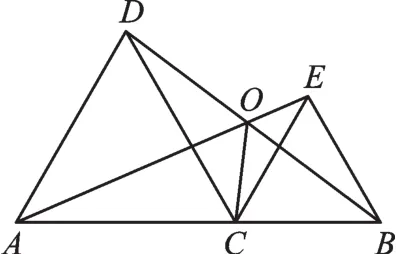
图3

【例2】如图3，△ACD、△BCE是等边三角形，且A、C、B共线，AE、BD相交于点O，连接OC.求证：OC平分∠AOB.

【分析】由△ACD、△BCE是等边三角形，不难得到△ACE≌△DCB.这一对全等三角形的作用何在？似乎与要证的∠AOC=∠BOC相距甚远，而∠AOC与∠BOC所在三角形显然不全等，所以转化成为必然.关于角平分线，本章学过它的判定定理：角的内部到角两边距离相等的点，在这个角的平分线上，由此可以转化为证明点C到OA、OB的距离相等（如图 4，即证 CM=CN）.如何证 CM=CN？由△ACE≌ △DCB可得：AE=BD、S△ACE=S△DCB，两个等底等面积的三角形必定等高，所以CM=CN.

图4

简证：作CM⊥OA于M、CN⊥OB于N.

易得：△ACE≌ △DCB，所以AE=BD，S△ACE=S△DCB.又因为CM⊥AE，CN⊥BD，所以CM=CN，故OC平分∠AOB.

延伸：若A、C、B三点不共线，其他条件不变，结论还成立吗？（因“不共线”对证明过程没有影响，所以方法不变，结论不变.）

总之，熟练掌握所学定理，是实现“转化”的前提.图3是本章的基本图形之一，证明OC平分∠AOB并不容易，利用角平分线判定定理实现转化是关键.本章基本图形和常用辅助线还有很多，我们只要对新知识及时巩固，并注意与旧知识之间的融会贯通，数学学习就能走上“快车道”了.