一种实用高效的安全多方排序协议

王 宁 顾昊旻 郑 彤

1(国网河南省电力公司信息通信公司 河南 郑州 450052)2(安徽继远软件有限公司基础运维分部 安徽 合肥 230088)

0 引 言

安全多方计算研究一组互不信任的参与方之间保护隐私的合作计算问题，最早由图灵奖得主姚期智先生于1982年提出[1]。文献[1]构造了这样一个问题(简称百万富翁问题)：两个百万富翁Alice和Bob在街头相遇，其中Alice拥有财富a，Bob拥有财富b。他们希望在不泄露自身财富信息的前提下比较出他们谁更富有，即两方秘密比较a和b的大小。此后，出现了很多解决百万富翁问题的安全方案[2-3]。

安全多方排序问题是百万富翁问题(两方秘密比较)的自然推广：假定有n个参与者P1,P2,…,Pn分别拥有隐私秘密x1,x2,…,xn(令X={x1,x2,…,xn})，他们希望在不泄露各自隐私秘密的前提下得到各自秘密在有序序列X′中的位置p(xi)，其中X′是X中n个秘密按从小到大排序的序列。排序问题是计算机科学领域最为重要并得到广泛研究的核心问题之一，它是求解许多复杂问题的基本构成单元。同样地，安全多方排序在保护用户隐私的多方协作计算领域有着很重要的应用价值，是很多复杂协议的基础协议。例如，保护用户隐私的电子投标和拍卖[4]、保护用户隐私的在线电子交易[5]、保密数据库查询[6]等。

目前，国外对安全多方排序问题的研究成果并不多。在为数不多的研究成果中，多数作者采用了基于比较的排序思想，因而至少需要Ω(nlogn)次两方秘密比较。例如，2011年，文献[7]基于排序网络提出了一个安全多方排序协议。该协议需要执行O(log2n)轮，总的计算和通信开销均为O(nlog2n)。文献[8]提出了一个随机化的安全希尔排序协议，以较高概率成功排序，需要执行O(log2n)轮，通信和计算开销均为O(nlogn)。同年，文献[9]提出了两个基于比较的常数阶轮次的安全排序协议，其通信和计算复杂性均为O(Nn)或O(n2)，其中N表示隐私秘密的范围大小。文献[10]基于快速排序提出了另一个有效的安全多方排序协议，需要执行O(logn)轮，其中通信和计算开销也均为O(nlogn)。

国内也有一些很好的研究成果。2007年，刘文等[11]利用EIGamal密码体制提出了一个安全多方多数据的排序协议，保证协议在常数轮的情形下，其通信复杂性为O(n2Nlgp)，计算复杂性为O(nN+k1+k2+…+kn)lgp)。2009年，邱梅等[12]利用RSA密码体制提出了另一个安全多方多数据排序协议，其原理与性能与文献[11]相当。2008年，李顺东等[13]基于离散对数困难性假设提出了一个高效的安全多方排序协议，其通信和计算复杂性均为O(n)。同年，肖倩等[14]基于同态加密提出了两种安全多方排序协议，继而基于模糊贴近度提出了另一种高效的多方排序协议，其计算和通信复杂性均降为线性O(n)。但是文献[13]和文献[14]中的协议均需要O(n)轮，特别是这两个协议均不是公平的协议，其中有一个特殊的参与者P1，他与某个(或几个)参与者联合可以很容易得到其他参与者的隐私秘密。

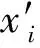
本文中，我们受文献[15]中数据扩张的启示，反过来，采用数据压缩的思想，结合巧妙的编码以及高效的安全多方求和方法，提出了一个新的安全多方排序协议。与已有协议相比，建议的协议很好地兼顾了安全性、有效性、公平性，因而更实用。

1 预备知识

1.1 线性时间排序

对于排序问题，有很多经典的求解算法，例如:插入排序、快速排序、合并排序、堆排序等。以上这些均是基于比较的排序算法。基于比较的排序算法最坏情况下的时间复杂性的下界为Ω(nlogn)。当然，也存在其他更有效的排序算法，例如计数排序和桶排序[16]。计数排序的基本思想是对每一个输入元素x，确定出小于x的元素个数。有了这个信息就可把x直接放到它在最终输出数组中的位置上。在下面的算法中假定n个输入元素中的每一个都是介于1到k之间的整数。

算法1计数排序

输入：数组A[n]，k

//A[n]存放待排序的n个数

输出：数组B[n]

//B[n]存放排序后的n个数

1. fori←1 tok

2. doC[i]←0

3. forj←1 ton

4. doC[A[j]]←C[A[j]]+1

//C[i]现在包含等于

//i的元素个数

5. fori←2 tok

6. doC[i]←C[i]+C[i-1]

//C[i]现在包含小于

//或等于i的元素个数

7. forj←ndownto 1

8. doB[C[A[j]]]←A[j]

9.C[A[j]]←C[A[j]]-1

若k=O(n)，则计数排序的时间复杂性为O(n)。在上面计数排序算法中，最关键的两个步骤分别是：计算等于i的元素个数，存储于C[i]中；计算小于或等于i的元素个数，存储于新的C[i]中(更新C[i])。对于算法1，若在第4步中调用安全多方求和算法计算C[i]，并公开计算结果C[1]～C[n]，后面各参与者可以根据自身的隐私输入A[j]，计算小于等于C[A[j]]的值，从而判定自己的秘密在整个秘密序列中的有序位置。经过这样修改的算法1实质上就是一种安全多方排序算法，在计算时保证了各参与者的隐私输入。即，借鉴计数排序的思想，对安全多方排序问题的求解自然就转变为对安全多方求和问题的求解。但遗憾的是，计数排序并不是普适的，而是有一定的适用条件(适用于秘密较小的情形)。

此外，桶排序也是一种高效的排序算法，平均情形下其时间复杂性也为O(n)。它的思想就是把待排序区间划分成多个相同大小的子区间或称桶，然后将n个输入数分布到各个桶中去。为了得到有序序列，先对各个桶中的数进行排序，然后按次序把各桶中的元素列出来即可。

本文结合了计数排序和桶排的思想，引入高效的安全多方求和技术以及巧妙的编码方法，设计了一个安全有效的多方排序算法。

1.2 Paillier同态加密

在后面的安全多方求和协议中，我们引入了Paillier同态加密算法，这里先对其作简要介绍。在1999年欧密会上，法国数学家P.Paillier提出了一个概率公钥加密方案[17](以下简称Paillier加密)。具体方案如下：

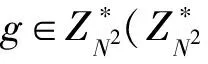
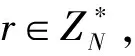
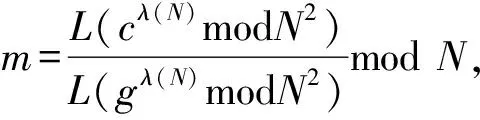
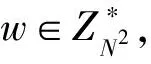
wλ(N)≡1modN

(1)

wNλ(N)≡1modN2

(2)

Paillier加密方案的安全基础是基于“计算合数剩余类假设”[17-19]定义函数εg：

(3)

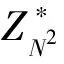
另外Paillier加密方案具有加法同态性质，即给定明文m1、m2，有:

gm1+m2(r1·r2)NmodN2(令r=r1·r2)=

E(m1+m2)

(4)

2 提出协议

实现思想：

1) 避免基于比较的排序方法，借鉴计数排序和桶排序的思想，所有参与者执行一次安全多方求和协议，计算小于各自秘密的秘密个数，从而确定各自秘密x在整个有序序列中应处的位置p(x)。

2) 为了提高效率，参与者先对各自的秘密x压缩得到x′，要求p(x)=p(x′)。

3) 进而对新秘密x′排序：在新秘密序列中统计小于各自新秘密的秘密个数l(x′)(l(x)=l(x′)。

4) 最终各参与者输出p(x)=l(x)+1，即各自秘密在有序序列中对应的位置。

协议1基于安全多方求和的安全多方排序

输入：各参与者Pi隐私输入秘密xi；

//假定各个参与者的秘密各不相同，且xi∈ZN。

输出：各参与者Pi输出p(xi)；

//即秘密xi在有序序列中对应的位置。

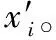
(1) 所有参与者随机选择一个小整数m。

//m是一个小整数，例如m=2,3,5。

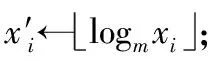
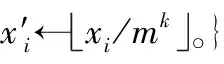
(1) 参与者计算d=└logmN┘ /k，其中k为划分的桶的个数，而d为每个桶的区间大小。

(2) 把整个待排序空间划分为k个区间(即k个桶)，分别为(0,d]，(d,2d]，…，((k-1)d,└logmN┘]。

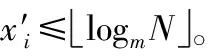
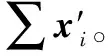
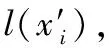
下面举例说明，假定有4个参与者：P1、P2、P3、P4，且假定他们各自的隐私秘密为32、2 216、15、354。即P1拥有32，P2拥有2 216，P3拥有15，P4拥有354。他们希望在保证各自隐私的前提下，实施安全的排序。

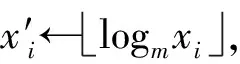
其次，所有参与方公开计算并确定两个用于划分桶的参数d、k。这里假定d=3、k=4，则四个桶对应四个区间(0,3]、(3,6]、(6,9]、(9,12]。因而5、11、3、8分别转换为向量(0，1，0，0)T、(0，0，0，1)T、(1，0，0，0)T、(0，0，1，0)T。这样对5、11、3、8的安全排序就转变为对向量(0，1，0，0)T、(0，0，0，1)T、(1，0，0，0)T、(0，0，1，0)T的安全多方求和。每个参与方，根据5进制(n+1进制)的编码方式，把各自的隐私向量转变为一个小整数。这里，(0,1,0,0)T对应52=25，(0,0,0,1)T对应50=1，(1,0,0,0)T对应53=125，(0,0,1,0)T对应51=5。最后，指定一个代理协助所有参与者执行一个安全多方求和协议(见协议2)，安全计算4个小整数的和25+1+125+5=156，再由代理把累加和156逆变换为5进制向量(1,1,1,1)T，并向所有参与者公开(1,1,1,1)T。

实际上(1,1,1,1)T=(0,1,0,0)T+(0,0,0,1)T+(1,0,0,0)T+(0,0,1,0)T。各参与者根据公开向量和(1,1,1,1)T及各自隐私向量，统计小于各自秘密的秘密个数，从而推算出原始秘密在整个有序序列中所应处的位置。P1得到l(5)=1，因而P1的秘密处于第2的位置；P2得到l(11)=3，因而P2的秘密处于第4的位置；P3得到l(3)=0，因而P3的秘密处于第1的位置；P4得到l(8)=2，因而P4的秘密处于第3的位置。实际上3<5<8<11，对应着15< 32<354<2 216。

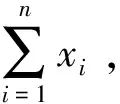
协议2小整数的安全多方求和

输入：各参与者Pi隐私输入秘密xi；

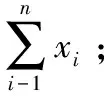
1) 每个参与者Pi(1≤i≤n)随机生成k个整数ai,1,ai,2，…，ai,k，其中k≤(n-1)/2，k的具体值可由Pi确定，而ai,j∈[0,p0](1≤j≤k)。接着参与者Pi随机选取k个其他参与者，假定为{Pi1，Pi2，…，Pik}。Pi分别计算gp0-ai,jmodN2，并把gp0-ai,jmodN2秘密发送给参与者Pij(1≤j≤k)。

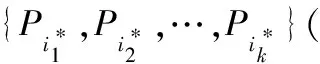
3) 收到其他所有参与者的秘密消息gp0-ai,jmodN2或gp0+ai,jmodN2后，每个参与者Pj(1≤j≤n)计算收到的所有秘密消息的乘积Gj。例如Pj分别收到P1、P3、P5的秘密消息gp0-a1,jmodN2、gp0+a3,jmodN2、gp0-a5,jmodN2，则Pj计算Gj=gp0-a1,jgp0+a3,jgp0-a5,jmodN2。

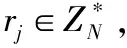
正确性证明：

(gp0+aj,1gp0+aj,2…gp0+aj,k)]}modN2=

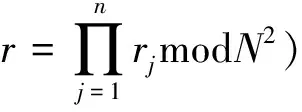
(5)

3 协议分析

对于任意的秘密xi和xj，有以下定理1成立。进而，对于任意的不同秘密xi和xj，有以下定理2成立。

定理1假定参与者Pi、Pj的隐私输入分别为xi、xj，则有：

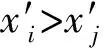
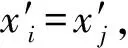
其中xi=xj的概率为1/(m└logmxi┘+1-m└logmxi┘)，反之xi≠xj的概率为1-1/(m└logmxi┘+1-m└logmxi┘)。

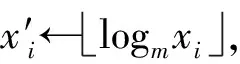
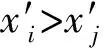
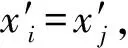
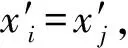
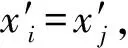
[(N-m└logmN┘)(N-m└logmN┘-1)]=

(6)

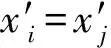
(7)

若N=ms(其中m为小整数)，则:

(8)

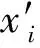
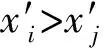
协议1中，若选择一个随机的m并执行秘密排序1次，各参与者的输出结果可能不是正确解，而是近似解，其最大误差为所属桶内的秘密个数。显然，当xi所在桶内只有一个秘密时，计算得到的l(xi)是正确的，从而p(xi)是正确的。实际上根据累加向量和，参与者可以判断自己获得的解p(xi)是否正确。为了提高精度，可以通过协议1的多次执行(即重新选择m重新计算p(xi))，各参与者总能得到正确的输出。此外，协议1也适宜于每个参与者拥有多个秘密的情形。与单个秘密情形有所不同的仅仅是“在协议1的第2步中的第3小步骤中，根据公开划分的桶，每方将得到一个多个分量为1(对应多个秘密)的0/1向量”，其他计算步骤不变。

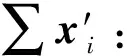
定理4在半诚实模型下，协议2是安全的。

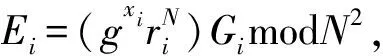
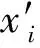
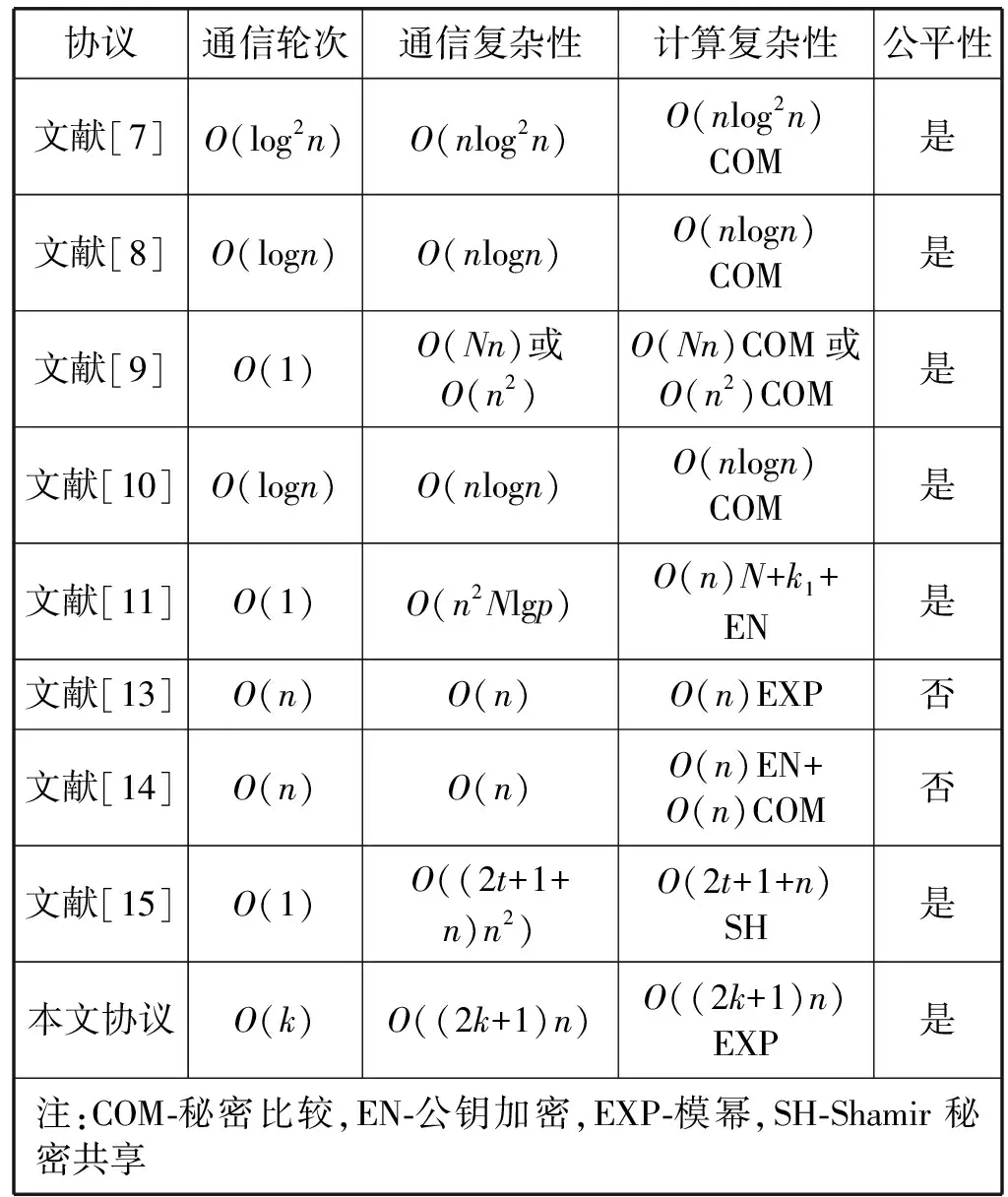
表1 各主流协议的比较

由表1可知，与其他主流协议相比，我们的协议整体性能占势：计算开销相对较低，主要操作为模幂运算，其他的加法、整数与向量转换等操作均为轻量级可忽略不计。总的通信带宽相对较低，主要用于小整数的安全多方求和，特别地保证了协议的公平性，而且没有秘密泄露。

4 结 语

避免传统的基于比较的排序方法，借助计数排序和桶排序的思想，把安全多方排序归约为安全多方求和。结合一种巧妙的编码方法，设计了一个安全、高效的多方排序协议。尽管安全和效率是一对矛盾体，但建议的协议使用灵活，可以根据安全等级，动态调整相应的安全策略。安全性高的，通信代价也相应高，上限为O(n2)；反之，通信代价低，理论上可达O(n)。与主流协议相比，综合性能优，保证了协议的公平性，能够在常数轮内有效实现。此外，能够满足参与者拥有多个隐私秘密的排序情形。因而建议的协议有着很好的应用前景，特别地，可作为基础协议应用于分布式网络环境下保护用户隐私的多方协作计算中。