基于混合核函数和高阶容积卡尔曼滤波的神经网络训练算法

张 沫 章 彪

(浙江邮电职业技术学院 浙江 绍兴 312000)

0 引 言

神经网络是一种由模拟人脑信息处理和存储的神经元而组成的数学模型，由于其结构简单，容易实现，以及极强的非线性映射能力，目前已经广泛应用在图像处理、语音识别和航空航天等领域[1]。

核函数是神经网络训练效果好坏的关键[2]。现有的核函数多种多样，不同的核函数非线性处理能力不同，神经网络的训练效果极大地受所选核函数的影响。目前，按照核函数学习能力的不同，核函数可以分为局部核函数和全局核函数。局部核函数在测试点附近的学习能力较强，相反，全局核函数在远离测试点的外推能力较强。因此如果基于单一的核函数进行神经网络训练往往会有局限性。因此混合核函数应运而生，它是将局部核函数和全局核函数线性组合而构成[3-4]。由于混合核函数同时具有学习能力和外推能力，能够准确地反映实际样本特性，因此利用混合核函数进行神经网络训练是提高训练精度的必然选择。

对于实际的非线性系统而言，由于多种不确定因素的影响，精确建模是相当困难的，一种简单可行的办法是利用神经网络对模型进行非线性近似。系统有内部状态和外部输出，通过观测外部输出来推得内部状态，而他们之间的关系可以通过状态空间模型法进行描述，不管内部状态与外部输出之间的关系多么复杂，该方法都能利用系统的输出数据对状态进行预测和估计。有了系统的状态空间模型之后，就可以用相应的滤波方法估计系统的状态[5]。基于状态空间的输出数据，在某种准则下对系统状态进行估计，那么就可以获得系统的状态值，同时也可以得到神经网络的参数。

将非线性滤波应用到神经网络的参数辨识上一直以来都是学者们研究的热点。扩展卡尔曼滤波(EKF)是一种应用最为广泛的非线性滤波方法，它的核心在于通过线性化方法将非线性系统近似成线性系统。文献[6]首先基于单个核函数的神经网络对系统建立状态空间模型，将神经网络的训练看作成非线性系统的参数识别问题，其中网络权重的迭代更新通过EKF算法的时间更新和测量更新步骤实现。然而实际中一些复杂的非线性系统对应的数学模型往往非线性很强，EKF的估计性能就会大幅度降低，甚至发散，其根本原因是EKF的一阶线性化近似忽略了Taylor展开式中的高阶项[7]。无迹卡尔曼滤波(UKF)无需对系统线性化，它是引用无迹变换对均值和方差进行处理，因此文献[8]应用UKF算法对神经网络权值进行在线更新。然而实际系统的维数可能较高，UKF就会遇到维数灾难问题。为了解决这个问题和进一步提高状态估计精度，文献[9]提出了HCKF算法，利用径向积分规则来最优化西格玛点和权重，大大增强了处理高维非线性状态的能力，估计精度和稳定性也明显得到了提高。基于容积卡尔曼滤波，文献[10]提出一种参数选择简单的多层感知器训练算法。由于HCKF算法比容积卡尔曼滤波算法的精度更高，文献[11]采用HCKF对扩维的状态进行训练更新得到网络的权值，并且仿真结果说明这种算法对权重估计的精度更高。

因此，本文首先建立混合核函数，并基于混合核函数建立状态空间神经网络模型，将神经网络的权值和系统的状态扩维成新的系统状态变量，然后采用HCKF算法对神经网络进行训练，进而提出基于混合核函数和HCKF的神经网络训练算法。

1 基于混合核函数的神经网络模型

高斯核函数、线性核函数、多项式核函数及Sigmoid核函数是目前常用的四种核函数。其中高斯核函数是局部核函数，剩下的三种核函数均是全局核函数[12]。由于局部核函数学习能力强，与之相反，全局核函数泛化能力强[13]，为了同时获得学习能力和泛化能力，本文选取混合核函数作为神经网络训练的基本核函数。记Kl(xi,xj)，Kg(xi,xj)分别表示局部核函数与全局核函数。混合核函数组合形式多样，为了便于讨论研究及说明其有效性，本文从最基本的线性组合入手，具体混合核函数Km(xi,xj)表示形式如下：

Km(xi,xj)=Kl(xi,xj)+Kg(xi,xj)

(1)

神经网络可以分为三层，分别为输入层、隐层和输出层，基于混合核函数的神经网络模型结构如图1所示。

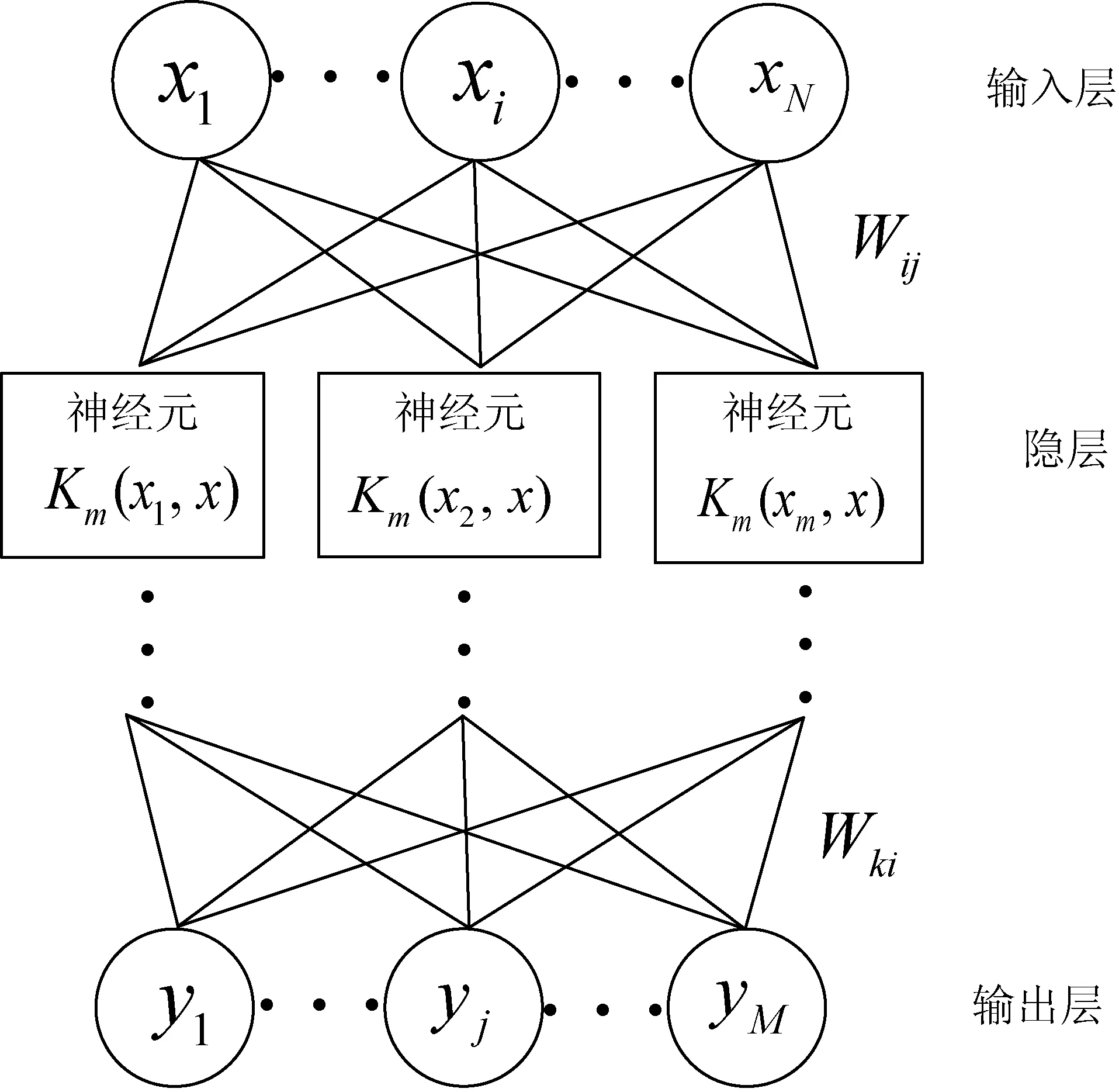
图1 神经网络的模型结构

其中，神经元Km(xi,xj)表示以Km(xi,xj)为基本核函数的神经元，输入的样本用x1,x2,…,xN表示，训练输出结果用y1,y2,…,ym表示，Wij,Wki表示网络权重。

2 高阶容积准则原理

考虑如下一般的离散非线性系统：

xk=f(xk-1)+wk

(2)

yk=h(xk)+vk

(3)

其中:式(2)为系统状态方程，f为已知的非线性函数，xk为n维的系统状态向量；式(3)为系统的观测方程，h为已知的非线性观测函数，yk为m维的观测向量；{wk}与{vk}为高斯白噪声，它们的均值都为零，方差分别为Q和R。

高阶容积准则原理如下[14]：

IUn(f)

(4)

IUn,2m+1(f)

(5)

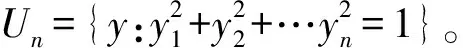
ωp

(6)

G{up}

(7)

式中：p=[p1,p2,…,pn]，|p|=p1+p2+…+pn，c(up)表示非零元素的个数。

进而利用高斯拉盖尔积分公式近似求解径向积分，寻找积分点rj及相应权值wr,j，使其满足如下公式：

(8)

式中：Nr为径向积分点总数。

记S(r)=rl为r的单项式，式(8)可以转化为：

(9)

因此，如果要得到2m+1阶径向积分准则，那么上式要对l=0,2,…,2m的积分精确成立，从而产生m+1个方程，进而求解该方程便可得到任意精度等级的径向积分准则积分点及权值的计算。

3 基于混合核函数和HCKF的神经网络训练算法

由于单一的局部核函数泛化能力太弱，而单一的全局核函数局部能力太弱，因此为了避免二者的弱势，而同时获得局部能力和泛化能力，本文首先将局部核函数和全局核函数线性组成混合核函数，基于该混合核函数对非线性系统建模逼近。由于非线性系统的状态是不知道的，也需要求解，因此，对状态和权重进行扩维，从而得到新的扩维状态。然后用HCKF算法对权重和状态进行训练，求解出系统的状态，得到最佳的网络权重，使得非线性系统的建模误差最小，具体的训练算法原理如图2所示。

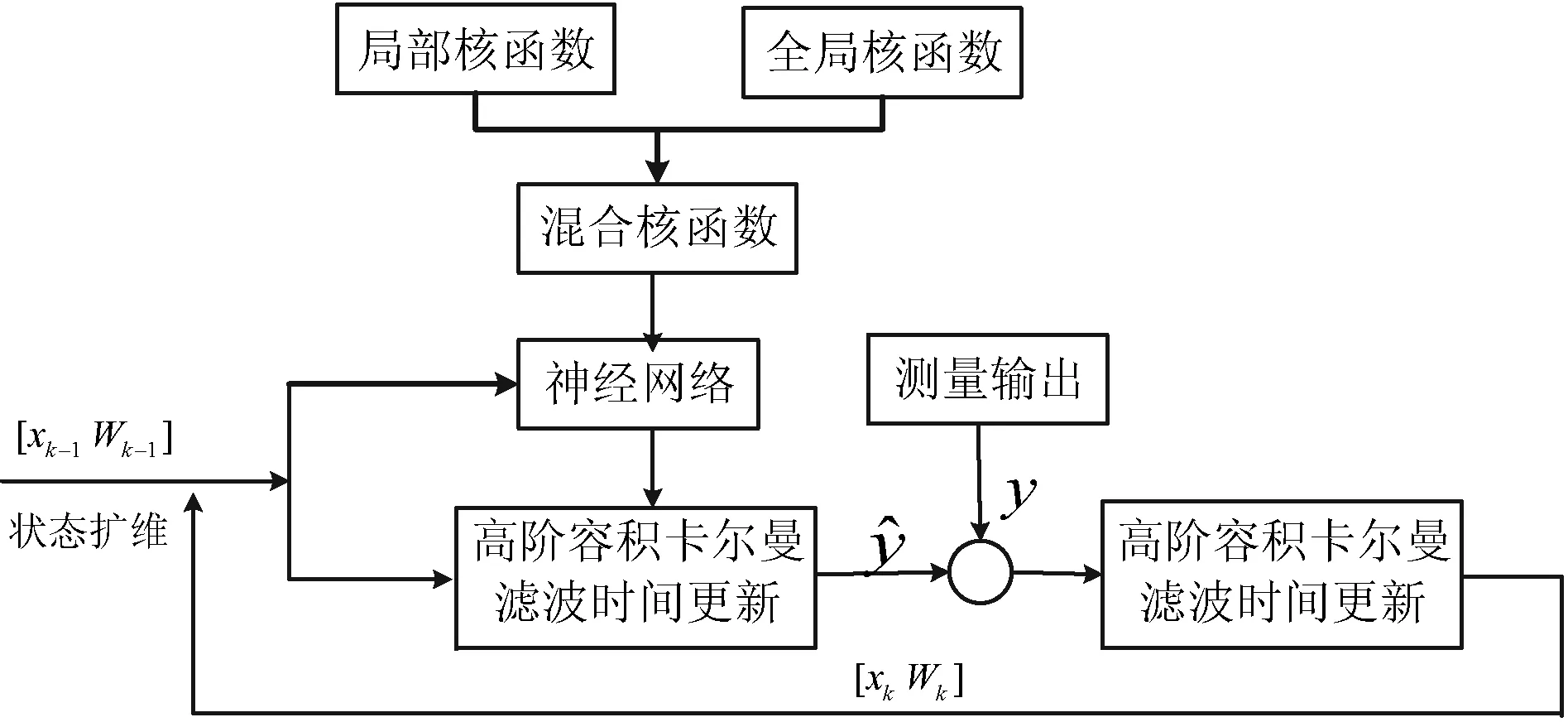
图2 训练算法原理

图2中，选择局部核函数与全局核函数线性组合成为混合核函数，在k-1时刻，原系统状态xk-1与权重Wk-1经扩维后将[xk-1Wk-1]输入到基于混合核函数的神经网络模型中，利用HCKF对扩维状态进行时间更新步骤，结合观测数据进行时间更新得到k时刻系统扩维状态[xkWk]，并作为下次系统迭代的输入值。具体算法如下：

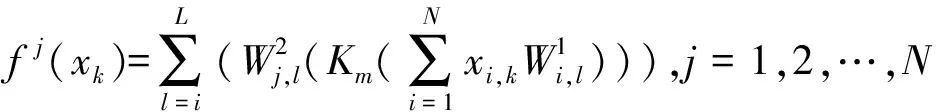
(10)

(11)

式中：Wk表示k时刻神经网络的权重，nk和sk为高斯白噪声，它们的均值为零，协方差矩阵分别为Nk和Mk。

进一步，利用HCKF进行时间更新：

① 记Pk-1|k-1为估计误差协方差矩阵，然后对其进行Cholesky分解可得下式：

(12)

式中：Sk-1|k-1为Pk-1|k-1的Cholesky分解结果。

② 用k-1时刻的Sk-1|k-1更新容积点：

(13)

式中：m=2n，且ξi的取值方法如下：

(14)

式中：ai表示矩阵B的第i列，B=[I-I]，I为单位矩阵，bi的表示如下：

(15)

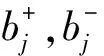
(16)

③ 更新传播容积点：

(17)

④ 更新一步状态预测值：

(18)

式中：wi的取法如下式所示：

(19)

⑤ 一步预测误差协方差矩阵的更新如下所示：

(20)

最后进行测量更新：

① 对一步预测误差协方差矩阵Pk|k-1进行Cholesky分解：

(21)

② 计算容积点:

(22)

③ 更新测量方程传播容积点:

(23)

④ 计算测量预测值:

(24)

⑤ 更新新息协方差矩阵:

(25)

⑥ 互协方差矩阵按如下公式进行更新:

(26)

⑦ 更新增益矩阵:

(27)

⑧ 计算k时刻估计值:

(28)

⑨ 更新误差协方差矩阵:

(29)

4 实验仿真

考虑一类典型离散非线性非静态增长模型如下所示[10]:

(31)

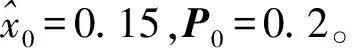
为了符号表示的简洁，对下列算法做如下标记：

MKF-HCKF：基于混合核函数和HCKF的神经网络训练算法。

MLP-CKF：基于容积卡尔曼滤波的神经网络训练算法。

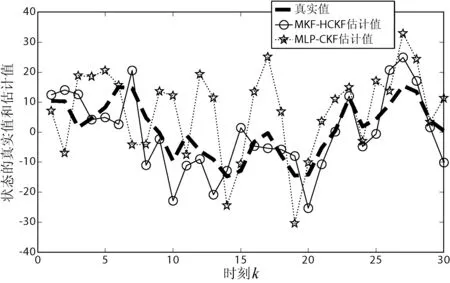
图3 状态估计曲线

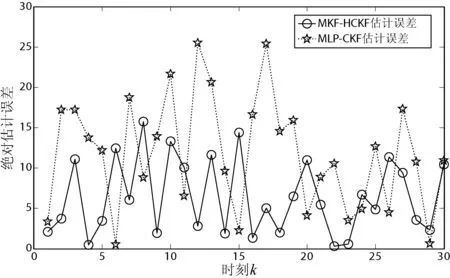
图4 状态估计误差曲线

表1 估计误差对比

图3和图4给出了MKF-HCKF、MLP-CKF算法对系统状态的估计和平均绝对估计误差，从估计曲线来看，两种算法都是有效的，都能跟上真实值，从表1的统计数据来看，MKF-HCKF算法的估计精度明显高于MLP-CKF算法，平均估计误差绝对值更小。这主要是因为MKF-HCKF算法的神经网络使用了混合核函数作为训练的核函数，而混合核函数更能反映样本的真实特性，从而使得估计精度更高。

5 结 语

本文提出了一种基于混合核函数和HCKF的神经网络训练算法。将常用的局部核函数高斯核函数与常用的全局核函数多项式核函数进行组合成混合核函数，如此形成的混合核函数同时具有学习能力和泛化能力，并基于该混合核函数对非线性系统进行建模，最后利用HCKF算法对扩维状态进行实时训练估计。本文算法提高了非线性滤波算法对神经网络的训练精度，仿真对比表明了本文所提算法的有效性。