面向科研社交网络的小同行双向推荐算法

刘 雪 晴

(复旦大学软件学院 上海 201203)

0 引 言

由于信息技术的迅猛发展与普及，科研人员开展学术活动的形式不再局限于会议、讨论等线下互动。很多科研工作者开始在各类不同的科研社交平台上寻找感兴趣的小同行及其群体，查看彼此的简历，与各地的科研人员互相分享研究成果、交换意见和建议，构成了一个覆盖全世界的科研社交网络。和其他社交网络一样，它也面临着信息过载的问题。推荐系统是用来解决信息过载问题的重要方法之一，可以主动满足用户的个性化信息需求[1]。因此，基于科研社交网络的推荐研究非常重要。

基于科研社交网络的推荐系统主要从以下三个方向展开：推荐科研成果、推荐科研人员、推荐科研社群。对于科研工作者来说，一个合适的同行研究者，带来的不仅仅是有效的学术交流，更是显著的知识发现，对科研工作者生产力和创新力的提高提供一定的帮助。智能的科研小同行推荐系统可以有效地帮助科研人员更快地找到更合适的科研合作者，从而提高他们的学术竞争力。现有的基于科研社交网络的科研人员推荐主要包括专家推荐[2]、合著者推荐。汪俊等[3]通过对科研社交网络中科研人员的知识与社会关系信息进行挖掘，构建了链接预测模型实现专家推荐服务。文献[4]基于结构分析研究人员基于研究机构的关系及其与外部研究人员间的关系，构建了多元的科研社交模型，应用到巴西在线科研社区中获得了很好的推荐效果。文献[5]基于合作者网络，构建了一个随机游走模型，为科研人员推荐潜在的科研合作者和科研合作群体。可以看出，目前的科研合作者研究虽然混合使用了基于内容推荐[6-7]、基于社交网络推荐[8-9]、基于协同过滤推荐[10-12]的方法对科研社交网络进行挖掘，但是仍然缺乏一个考虑双向意愿的推荐机制。实际上，科研人员无论从基于内容还是基于行为的角度，都隐含着自己的偏好。是否选择和另一个科研人员一起合作研究，需要同时满足双方的偏好，才能建立小同行链接，才算一个成功的推荐。为了弥补传统推荐算法的这种不足，基于互惠性的双向推荐[13-16]引起了国内外学者的广泛关注。

小同行推荐这个应用场景本质上是用户到用户的推荐，参与的双方既是服务用户，又是待推荐用户，他们不仅在研究兴趣偏好和行为偏好上相似，而且双方的偏好都需要得到满足，达到互惠的推荐效果，这也是双向推荐技术的基本前提。然而在科研社交网络中现有的推荐研究基本上只考虑一方的需求，很少有研究讨论互惠性的概念。因此本文在挖掘科研人员基于相似性的特征之后，利用科研人员的行为网络交互数据，挖掘基于协同过滤的互惠性。首先提出一种基于协同过滤的双向互惠小同行推荐模型CFRPR；随后融合科研人员的多维度特征相似度，通过对比基于协同过滤的双向推荐以及融合基于内容的互惠相似性，实验验证了本文算法的有效性。同时也证明了基于互惠性的双向推荐可以适当地解决推荐系统中存在的冷启动问题。

1 相关工作

与传统的推荐方法相比，参与双向推荐的双方都是具有自主选择能力的对象，因此匹配时需要满足双方的偏好。社交网络中的用户推荐与双向互惠性联系最为紧密，因为双向偏好的匹配直接决定了推荐的质量。文献[17]在基于社交网络的业务合作伙伴识别中应用了双向推荐，通过使用所属公司的简介和用户之间的事务关系生成候选人。文献[18]提出了一个三因素图模型，将其应用到社交网络中的双向链接预测。文献[19-20]将双向互惠性应用到在线交友推荐中。其中文献[20]通过同时考虑基于用户偏好相似度的局部度量和基于双向匹配的全局度量，提出了一个广义的双向互惠性推荐框架。通过在线约会网站和在线招聘网站上的实验，证明了其有效性。

文献[21]通过考虑双向链接，给出了一种基于混合协同过滤(HCF)的解决方案，在推荐初始联系和双向联系时均表现出了很高的性能。文献[22]采用基于内容的推荐算法学习双方用户的偏好相似度，同时利用用户之间的交互数据挖掘目标用户的隐式偏好，基于双向偏好匹配定义了一个新的评估度量(成功率)来评价算法的性能。该算法基于融合策略进行推荐，解决了推荐系统中最常见的冷启动问题。但该算法具有一定的局限性，仅适用于信息对称的推荐领域，具有一定的局限性。双向推荐还被应用到招聘中职位和求职者之间的匹配中[23]，通过引入本体的概念，构建了双向推荐系统。

总的来讲，基于内容与基于协同过滤相结合的双向混合推荐策略是目前最先进的互惠性研究。然而科研社交网络中现有的推荐研究基本上只考虑一方的需求，很少有研究讨论互惠性的概念。文献[24]在基于科研社交网络的导师推荐研究中考虑了用户之间性格偏好的匹配，但仅仅作为相似性度量的特征之一，并不能很好地度量用户在不同指标的双向偏好匹配程度，也没有强调互惠性的重要性。而小同行推荐本质上是一个双向互惠的任务，科研人员的双向意向将直接决定最终的推荐结果。因此如何将双向互惠性推荐应用到科研社交网络的推荐系统中将是本文重点研究的问题。

2 科研人员相似度特征提取

在小同行推荐这个情境下，科研人员想要寻找的是在某个特定学科/专业能有效地满足其专业知识需求，并且能通过个人社交网络方便地与其建立连接的目标用户。因此，在科研人员之间相似度的计算中，除了利用基本的学术信息，也需要近一步抽取社交网络相关特征。

本文在文献[24]已有的研究成果基础上提出基于多维度融合特征相似性的小同行推荐模型MSBPR(Multidimensional Similarity-based Peer Researcher Recommendation Model)。具体相似度计算方法如下：

1) 研究方向相似度(Expertise Similarity) 首先利用科研人员的科研成果相关信息、所参与基金项目的数量及相应等级信息，根据JCR的期刊分区情况和AHP的项目分类情况赋予相应的权重，结合G指数挖掘得到科研人员的学术质量度。在此基础上构建学术质量度加权的LDA模型，基于该主题分布首先得到科研人员的研究方向相似性：

(1)

式中：θv是候选科研人员v的研究方向主题分布，θu,v是科研人员u和v的联合平均分布，表示二者研究方向的联合分布。通过计算各自与联合分布的距离来度量科研人员之间的研究方向匹配程度。

2) 基于个体层次的连接度(Individual Connectivity) 基于科研社交网络上的合著者网络，混合使用基于邻居和基于路径的相似度度量方法挖掘科研人员基于个体层次的连接度：

IdCon(u,v)=δNPro(u,v)+(1-δ)PPro(u,v)

(2)

式中：δ是根据科研人员在网络中的连接度引入的平滑参数。NPro(u,v)是科研人员u与v基于Adamic-Adar方法的邻居距离(Neighbor Proximity)。PPro(u,v)是两个科研人员基于最短路径的相似度(Path Proximity)。

3) 基于机构层次的连接度(Institutional Connectivity) 在选择小同行建立合作关系时，所属机构之间的合作连接也会影响结果[25]。本文基于机构间的合作网络挖掘两个科研人员u与v基于机构的连接度：

(3)

式中：ΓIu表示用户u所属机构Iu的所有科研产出集合。分数的分子表示两个机构的共同科研产出数量，分母则表示两个科研人员所隶属机构的科研产出总和。

4) 基于多维度特征的相似度(Combining Similarity) 利用一种基于分值的无监督学习方法——Comb-MNZ算法，来融合上述度量得到科研人员基于多维度特征的相似度度量：

(4)

(5)

式中：NR表示所有特征的数量，τ(v,NR)表示候选研究人员v在集合R中的出现频率。Scorenorm(v,Rn)为候选研究人员v在特征n上正则化分数。特征总数量为f，基于贪心策略为每个特征分配权重wn。

至此，将每位候选科研人员与目标科研人员的相似度用融合后的分值(式(4))来度量，可以根据该得分来预测每个候选科研人员被推荐为小同行的概率。根据高低排序可以过滤候选推荐列表。

3 基于协同过滤的双向互惠推荐

除了用户相关的内容信息，科研社区中还收集了大量与科研人员相关的行为数据。例如，当一个用户选择与其他科研人员建立好友关系、合作关系时，或是回复别人的消息时，系统都会产生记录，而这些记录中也蕴含着科研人员的偏好。

3.1 上下文与符号

本文将科研人员在科研社区中的交互表示为一个双向网络，其中一个节点代表一个科研人员，双向网络的边通常连接着两个研究兴趣相近的用户。在许多科研社区中，如果科研人员x对另一个科研人员y感兴趣的话，他通常会发送一条简单的预设信息，例如“对您的研究方向很感兴趣，是否有机会一起合作？”或者一个好友申请，本文将其定义为初始联系IC(Initial Contact)。如果y也对x感兴趣，他/她可以发送一个回复(Reply)给x，这就构成了两个科研人员之间的双向联系RC(Reciprocal Contact)。本文将由这种双向联系组成的网络定义为小同行网络。图1描述了基于科研社区的一个交互网络案例。

图1 基于科研社区的一个交互网络案例

其中所有科研人员构成了用户集合U，本文将需要推荐服务的科研人员定义为服务用户S，其中S⊆U。N=|S|是服务用户的数量。M=|U|是科研人员的总数量(N≤M)。本文将服务用户从所有用户(科研人员)群里分离出来，是因为基于协同过滤的模型在拥有更多历史行为的用户群体上会表现得更好。

无论是初始联系还是双向联系，都包含着用户的行为偏好信息。从联系的定义可以得到，由服务用户发起的初始联系包含了服务用户对候选用户的“品位”，而候选用户选择发送回复，则说明该服务用户与候选用户的偏好相匹配，本文将其定义为服务用户的“吸引力”。通过考虑服务用户和候选用户之间偏好及吸引力的匹配，定义基于协同过滤的互惠性特征。在用户尝试与其感兴趣的科研人员建立小同行链接的应用背景下，尝试通过提高服务用户得到候选科研人员回应的概率，以提升推荐的性能。

3.2 CFBPR模型

本文使用经典协同过滤小同行推荐模型CFBPR(CF-Based Peer Recommendation Model)作为第一个基准模型，并基于该模型对科研人员的偏好建模，分以下三步进行：

(1) 将科研人员的交互行为表示为一个M×N的链接矩阵C。在二分矩阵C中，如果科研人员i向科研人员j发起了初始联系，则无论科研人员是否回复了科研人员i，都有Ci,j=1，否则Ci,j=0。因此，该矩阵的行表示一个服务用户的所有初始联系行为并且反映了他/她的偏好。图2展示了一个初始联系矩阵案例。

图2 联系矩阵：CFBPR模型

(2) 计算服务用户u和w之间基于协同过滤的相似度CFSim(u,w)。在本文中，使用矩阵C中科研人员u和w行向量的余弦相似度来度量。相似度越高，表示两个科研人员在选择小同行时有着越相似的品位,即他们请求联系了相似的科研人员。

(3) 候选科研人员推荐排序。对于一个服务用户u，模型会对每一个与u还未有过互动行为的候选科研人员v(v∈U并且v≠u)进行迭代，计算u与v之间(将v推荐给u)的推荐成功分数：

(6)

基于该分数对候选列表进行排序，分数越高，科研人员v越可能被推荐给u。该模型的基本思想是越多与服务用户u偏好相似的学者向科研人员v发送初始联系，科研人员v越可能会是u的潜在小同行。

3.3 ROPR模型

为了与最终的模型做对比，提出一个只考虑双向联系的模型ROPR(Reciprocity-only Peer Recommendation Model)作为另一个基准模型。即在该模型的二分联系矩阵中，只有当科研人员i与j之间有着双向联系时才会有Ci,j=1(不管由谁发起初始联系)，否则Ci,j=0。即使科研人员i单方面联系/关注了j，只要j不回复，那么Ci,j仍为0。联系矩阵具体见图3。因此，该矩阵的行既表示了一个用户的品位，也表示了他/她的吸引力。

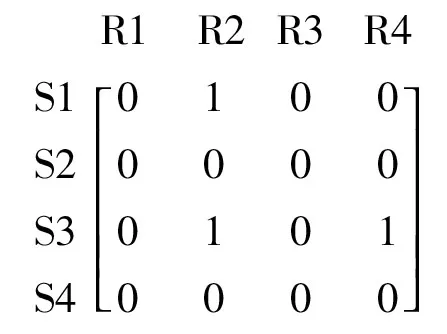
图3 联系矩阵：ROPR模型

相似度的计算方法及小同行的推荐方法均与基准CF模型保持一致。该模型的主要思想为：只有当候选科研人员v对服务用户u感兴趣并且吸引了与u有相似偏好及吸引力的科研人员，科研人员v才会被推荐给u。

3.4 CFRPR模型

ROPR模型虽然能够描述用户间基于协同过滤的显示偏好(品位和吸引力)，它仍有两个限制：

1) 忽略了初始联系请求未被回应的情况下隐含的科研人员偏好信息。例如图3中S1的行向量为空，因此无法不能追踪他的品位。

2) 未利用不回复初始联系行为所隐含的负反馈偏好信息。例如，当R2选择不回应S2的初始联系，这表示S2的吸引力与R2的品位不匹配。对于与S2有相似吸引力的用户，R2可能不是一个好的候选推荐。

这两个限制会影响用户的互惠性特征计算。例如，图3中S2和S4都联系了用户R4，但都没有得到回复，这种隐式品位相似性和吸引力相似性并没有在该模型中体现出来，因而无法得到准确的科研人员互惠性特征。

通过同时考虑初始联系和双向联系，本文提出了一个基于协同过滤的双向推荐模型CFRPR(CF-based Reciprocal Peer Recommendation Model)，挖掘科研人员的显式偏好和隐式偏好，对科研人员基于协同过滤的互惠性特征建模。这样一来，联系矩阵C则变成了一个三维矩阵。为了简化，本文仍然用一个二维矩阵来表示它：

ci,j=

(7)

当科研人员i发送了一个信息(初始联系或者回复联系)给科研人员j(意味着j的吸引力与i的品位相匹配)，那么此时Ci,j,1=1，否则Ci,j,1=0，表示i对j不感兴趣。同样地，如果科研人员j对科研人员i感兴趣，Ci,j,2=1，反之Ci,j,2=0。图4是混合模型的一个联系矩阵案例。

图4 联系矩阵：CFRPR模型

该矩阵可以分为两个二分矩阵，分别表示服务用户和候选科研人员的品位。由于候选科研人员的偏好会反映服务用户的吸引力，反之亦然。

为了简化说明，仍旧基于二维联系矩阵来综合考虑三种科研人员之间的相似性度量：

1) 品位相似性——两个科研人员对相似的科研人员感兴趣。

2) 吸引力相似性——两个科研人员吸引了相似的科研人员。

3) 负反馈偏好相似性——两个科研人员拒绝了相似的用户/被相似的科研人员拒绝。

因此将两个科研人员u和w之间基于协同过滤的相似度表示为：

其中函数f需要满足以下条件：

1)f(,)=fmax

x1=x2 andy1=y2 andx1+x2+y1+y2>0;

2)f(,)=fmin

x1≠x2 andy1≠y2;

3)f(,)=fmin

x1=x2=y1=y2=0。

它表示在计算科研人员间相似度时，品位和吸引力均相似(即双向匹配)的科研人员会得到最高的分数，而品位和吸引力均不同的科研人员则会获得最低的相似性度量。考虑以上条件，对函数f定义如下：

f(,)=

(8)

式中：⊕表示异或操作，会产生三个不同的值：当品位和吸引力均匹配时取2；单向匹配时取1；无匹配时取0。式子的分母dgr(u)+dgr(w)用来做归一化处理，防止相似性向受欢迎的研究者倾斜，从而影响互惠性的计算。其中dgr(i)是科研人员i在无向网络和无权重网络中的中心度。

最后，得到用户u与v基于协同过滤的互惠性：

(9)

式中：weight(ck,v)是综合考虑品位、吸引力不同匹配情况的权重，定义如下：

(10)

从式(10)可以看出，本文对品位和吸引力双向匹配的情况赋予完全权重，并为单向匹配分配一个惩罚因子s。

互惠性特征度量CFRec(u,v)就是将v推荐给u的成功分数：

RScore(u,v)=CFRec(u,v)

(11)

根据该分数的高低为服务用户u生成最终的科研人员推荐排序列表。

根据小同行的定义，推荐结果追求的是科研人员双方偏好及吸引力同样程度的匹配。因此在本文的研究中不区分偏好和吸引力的重要性，将其都归为单向匹配。拓展到其他应用场景中，可以通过为f(cp,k,cq,k)定义不同的计算方法来进行区分。例如在专家推荐中，服务用户想要寻找的是一个与自己的偏好(尤其是某特定领域上的偏好)高度匹配的科研人员，因此可以在双向推荐中赋予偏好匹配更高的权重。即在偏好和吸引力单向匹配的情况下，可以令f(cp,k,cq,k)的取值满足：

f(<1,0>,<1,0>)>f(<0,1>,<0,1>)

(12)

同时，在计算最终的互惠性时，可以对偏好单向匹配和吸引力单向匹配分配不同的惩罚因子：

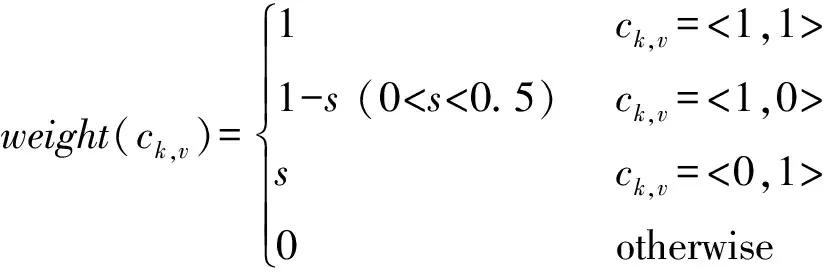
(13)

总的来说，本模型以经典CF模型为原始模型，主要从两个方向进行基于双向互惠性的拓展：

1) 针对被推荐的科研人员，在计算科研人员间相似度的时候考虑了“品位”和“吸引力”的双向相似：偏好及吸引力均相似的科研人员之间的相似度要高于单向偏好/吸引力相似的科研人员。

2) 在进行推荐时，考虑“品位”和“吸引力”的双向匹配：与服务用户的“品味”和“吸引力”度量均匹配的科研人员最可能被推荐。相比只考虑单方面偏好的匹配成功率更高。

在本方法中，默认品味和吸引力在双向匹配中有着相同的重要性。

4 基于混合互惠性的双向推荐

在第3节中基于协同过滤进行了双向推荐的拓展，通过考虑服务用户和候选用户之间的双向偏好(即3.1节中定义的“品味”和“吸引力”)，得到了科研人员基于协同过滤的互惠性特征CFRec(u,v)。现有文献对互惠性的研究证明了基于内容和基于协同过滤的混合双向推荐是最有效的方法。因此结合第2节中科研人员基于研究方向和科研社交网络的融合相似性CSim(u,v)，提出一种新颖的基于混合互惠性的双向推荐算法CRBPR(Combing Reciprocity-based Peer Recommendation Model)，详细描述见算法1。

算法1基于混合互惠性的双向推荐算法CRBPR

Input: Service Userr,

N number of recommendation candidatesc

Output: List of RecommendationsRFinal

Method:

1findr’s research interests preferencePr

2foreachcandidatecdo

3/*modeling combing similarity forrandcfromr*/

4S(r,c)←CSim(r,c)

5ifS(r,c)>0thenfindc’s interests preferencePc

6/*modeling combing similarity forrandcfromc*/

7S(c,r)←CSim(c,r)

8/*calculate the content-based reciprocity forrandc

*/

9ConBRec(r,c)←f1(S(r,c),S(c,r))

10/*sort the candidates generate the candidate list of

recommendationRC*/

11for∀i≤N

12IfConBRec(r,ci)>ConBRec(r,ci+1)then

13sortR{c1,c2,…,cn}

14returnRC

15/*filter the candidate list*/

16foreachcandidatec∈RCdo

17/*calculate the combining reciprocity forrandc*/

18ComRec(r,c)←f2(ConBRec(r,c),CFRec(r,c))

19/*sort the candidates and generate the list of

recommendation */

20for∀i≤M=|RC|

21IfComRec(r,ci)>ComRec(r,ci+1)then

22sortRC{c1,c2,…,cm}

23returnRFinal

由于多维度融合相似性CSim(u,v)是根据对科研人员概要进行挖掘，其中包括个人简介、论文信息、科研社交网络等内容。因此本文将基于这种相似性计算得到的互惠特征称为科研人员基于内容的互惠性，即算法1中第9行的f1函数具体计算式如下：

ConBRec(u,v)=f1(u,v)=

(14)

式中:CSim(u,v)为候选科研人员v基于内容满足服务用户u的程度；CSim(v,u)为服务用户u基于内容满足候选科研人员v的程度。

本文使用调和平均数将双方的相似度值联系起来，通过其特有的调和作用，避免了在各自相似度值的差异度较大时对互惠性值所造成的影响。同时还可以反映用户之间基于内容互相选择的程度。这说明科研人员在研究方向以及社交网络连接等多维度的双向匹配程度，可以生成基于内容互惠的候选列表。为了提高匹配的成功率，将第3节基于协同过滤的互惠性考虑进来，通过定义科研人员的联合互惠性，近一步过滤候选科研人员，生成最终的小同行推荐列表，详细描述见算法1。

ComRec(r,c)=α×ConBRec(u,v)+β×CFRec(u,v)

(15)

式中：参数α和β是调节基于内容互惠性和基于协同过滤互惠性重要性的权重因子。当在选择小同行时，对研究内容相关的互惠双向匹配更看重时，可以根据训练集的训练结果相应地调大α的值；反之，如果科研人员更在乎历史交互记录中的隐式匹配成功率，就需要将β调大。根据后述在测试数据集上的实验发现，一般β的值都要略小于α的值，这与科研社交网络中科研人员对小同行的匹配需求相符。并且，当取α=0.6,β=0.4时推荐效果最佳。

基于混合互惠性的双向推荐，是建立在双方研究兴趣范围一致且有链接建立意向的基础上做出最后的推荐。通过双向满足和互惠互利的方式，做到了最真实、最有效的小同行推荐。

5 实验与评估

5.1 数据集

AMiner是清华大学计算机科学与技术系知识工程研究室研发的科研社会网络搜索与挖掘系统，同时也是学术大数据深度挖掘和知识服务平台。Aimer使用机器学习方法，基于每个科研人员进行多个(科研)社交网络账户自动关联，从各个不同的主页以及账户自动抽取科研人员的相关信息。本文使用AMiner的公开数据集对模型进行描述与验证。由于现有科研社交网站的行为数据难获取，本文考虑从LinkedIn和Slashdot的平台数据集中获取。LinkedIn网站的用户之间有关注/不关注的链接关系，关注行为可以看作是一个初始联系，互相关注则看作是一个双向联系。Slashdot是一个科研朋友共享技术相关咨询的平台，允许用户互相标记为“朋友(喜欢)”或者“黑名单(不喜欢)”，因此也可以提取联系信息。结合已有的科研社交网络链接，对科研人员的行为偏好进行挖掘。

通过对数据集做档案匹配，提取了包含在176天内4 000名科研人员的小同行链接行为记录。其中有174 931个初始联系，其中25.8%最终变成了双向联系。

实验时，将前88天的科研人员交互行为用于训练，剩下的数据则作为测试数据集。本文选取了在训练集和测试集中均发送了超过5次初始联系的科研人员作为服务用户，大约总共有2 786个服务用户。训练集包含了41 558对小同行联系，测试集包含了42 766对小同行联系。

5.2 实验评估标准

推荐系统中对推荐质量的评估标准有很多，其中最常用的统计精度度量方法是准确率(Precision)、召回率(Recall)和调和平均数(F1值)，它们的计算公式如下：

准确率P：成功的推荐在所有推荐中所占的比例，体现的是推荐成功的比率。

(16)

召回率R：成功的推荐在所有已知成功的推荐中所占的比例，体现的是待推荐科研人员被推荐的比率。

(17)

式中：R为科研人员u的推荐列表；U为向科研人员u发起过小同行链接建立联系的科研人员集合。

综合以上两项指标，可用F1值来反映整体的推荐质量：

(18)

根据互惠性的定义，小同行推荐的结果是判断一个科研人员是否为另一个科研人员的小同行，因此可以直接通过是否建立小同行链接来判断推荐的效果。另外，使用平均绝对偏差(MAE)来评估算法的精确性。

平均绝对偏差(MAE):成功的推荐结果与预测的推荐之间的平均绝对偏差。

(19)

式中：predictu为预测的推荐列表；predictu,v为对科研人员v预测的匹配结果；realu,v为对科研人员实际的匹配结果；Nu为进行预测的推荐个数。

平均绝对偏差越小，则推荐算法的效果越好。

5.3 实验结果分析

5.3.1 基于MAE指标评价本文算法

首先基于第2节MSBPR模型的推荐结果，分别应用CFBPR模型、ROPR模型、CFRPR模型进一步对候选列表进行筛选排序，生成新的推荐列表。图5是四种算法在不同的小同行推荐数目下，MAE值的变化情况。

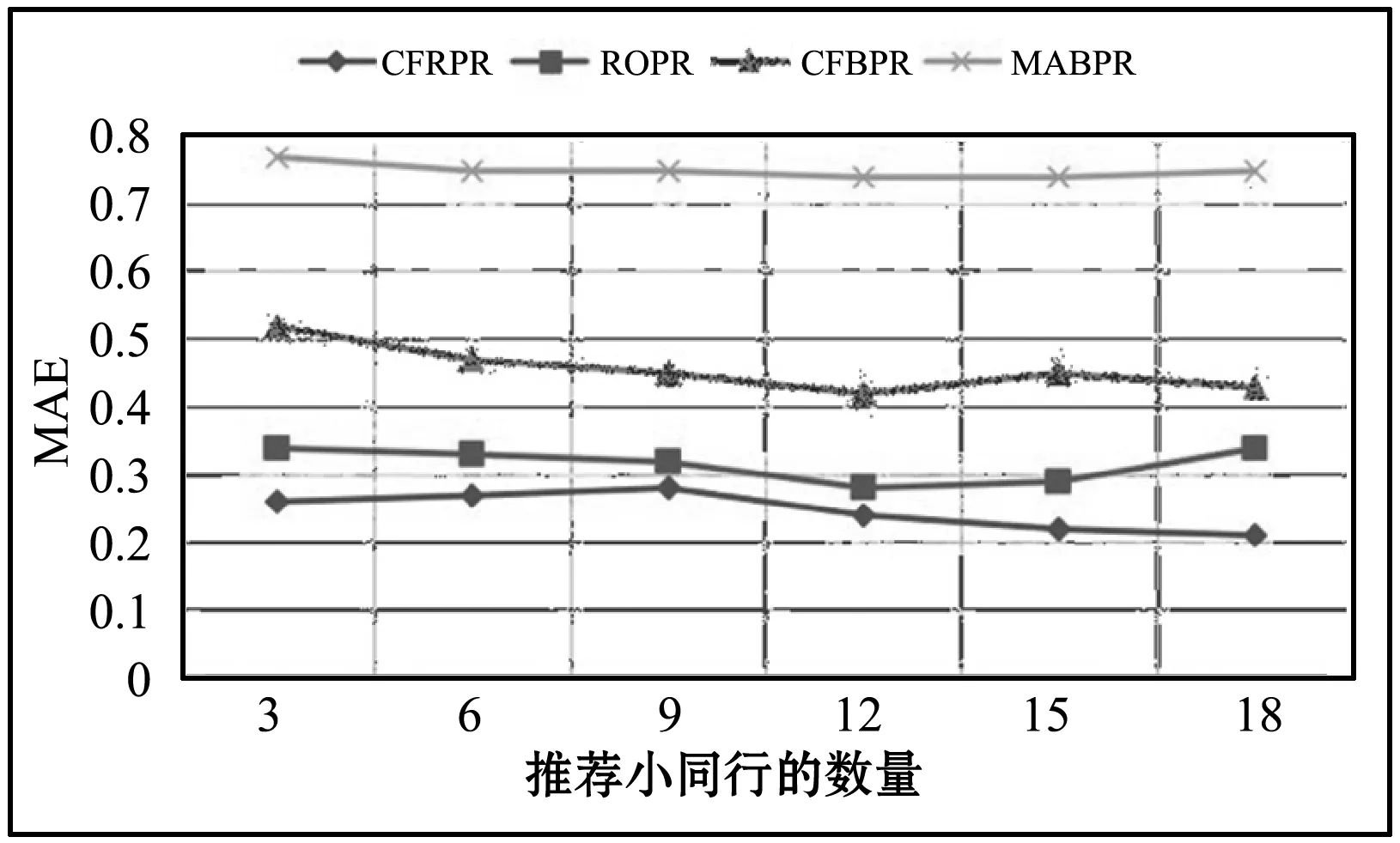
图5 基于相似性和基于互惠性算法的MAE比较

通过对比可以看出，本文所提出的小同行推荐中隐含的互惠性是有一定意义的，即使是基于传统协同过滤算法的互惠性扩展，也能够进一步降低预测结果与实际推荐结果之间的偏差。

5.3.2 基于Precision和Recall指标评价本文算法

为了近一步体现双向推荐的互惠性，本节给出了两套精度评估推荐性能的标准用于对比：

1) 基于初始联系IC(Initial Contacts)的标准:

IC Precision@K衡量推荐的K个候选人员中服务用户选择联系的科研人员数量在top K候选排名中的比例；IC Recall@K评估所有科研人员中服务用户选择联系的科研人员数量在top K候选排名中的比例。第二套标准强调双向互惠——一个初始联系是否得到回应。

2) 基于双向联系RC(reciprocal-contact)的标准：

RC Precision@K评估推荐的K个候选科研人员中最后有多少与服务用户建立了双向联系；RC Recall@K衡量与服务用户建立双向联系中的科研人员，有多少在topK推荐排名中。

针对混合模型，本文根据不同的惩罚因子s进行了测试。总体而言，随着s的增加，混合模型能够推荐更多潜在的双向联系，可以收获更好的基于RC的性能以及稍微低一点的基于IC的度量值。尽管所有s值下的混合模型测试都能得到较好的性能，但本文选择基于s=0.6与其他模型进行比较。因为这种情况下基于IC和基于RC的度量值对应的性能比较均衡。

图6显示了五种推荐方法的性能对比。总体上基于混合互惠性的双向推荐模型CRBPR表现得最好，并且基于RC基准的混合模型CRBPR是五种方法中表现最好的。首先分析CFBPR、ROPR、CFRPR这三种基于协同过滤的模型分别在基于IC和RC基准上的性能差异，可以通过它们利用科研人员“品位”和“吸引力”特征的不同方式来解释。CFBPR模型使用了科研人员的所有行为偏好信息却忽略了吸引力信息，因此它在基于IC的基准会表现得稍微好些，这是因为该基准下算法的性能只依赖于单向偏好的精准捕获。但是在基于RC的基准下，CFBPR的性能却远落后于ROPR和CFRPR模型。这是因为ROPR模型考虑了吸引力(通过初始联系的回复情况来表示)特征，但它忽略了科研人员行为数据中隐含的负反馈偏好。因此，ROPR模型在推荐符合科研人员“品位”的小同行时表现得较差，但提高了推荐用户被科研人员所吸引的可能。而混合模型CFBPR利用了这三种信息——用户的品位、吸引力和负反馈偏好，因此它在三者中总体上有更好的性能。然后，观察基于协同过滤互惠性的双向推荐模型CFBPR与基于混合互惠性的双向推荐模型CRBPR在小同行推荐结果基于RC的精度对比。可以发现，在推荐数目较小的时候，二者的差距不是很明显，但随着推荐数目的增加，基于RC的召回率呈上升的趋势。这是因为在大规模数据集中，召回率和准确率是两个互相制约的指标，召回率体现的是查全率，因此随着K的增大，召回率会相应地提高，而准确率则会逐渐下降。此时混合互惠性的优势也逐渐凸显，基于协同过滤的互惠性效果次之，但都要明显优于其余三种算法。

5.3.3 基于F值指标评价本文算法

图7是对本文提出的算法进行基于F值的对比。可以看到基于用户协同过滤推荐和基于内容相似性的推荐都只是将科研人员推荐给目标人员，而基于互惠性的考虑需要进行两次这样的单向匹配，从而进一步缩小了推荐范围，因此能够更加准确地定位候选推荐小同行。

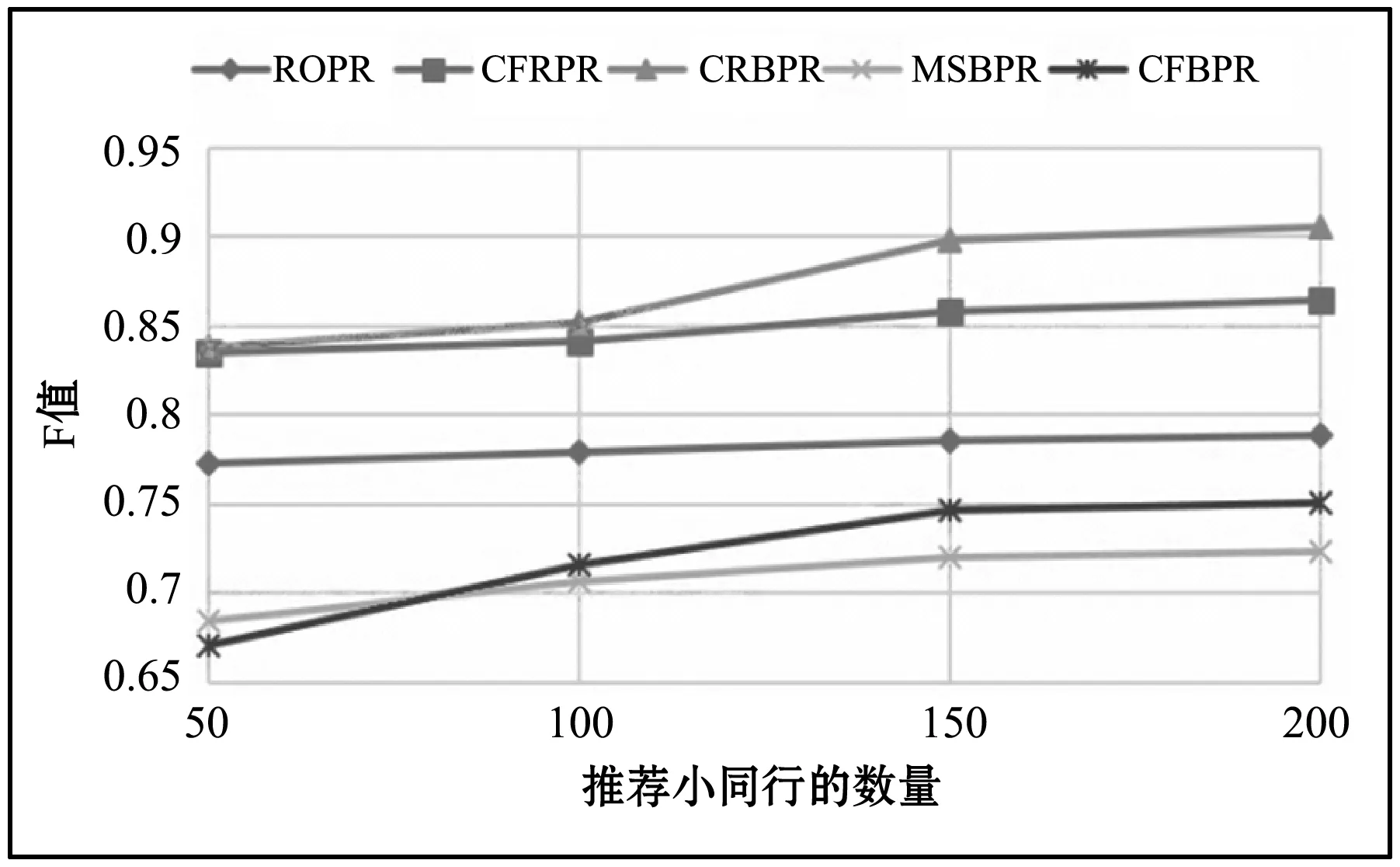
图7 基于相似性和基于互惠性算法的F值比较

从图7中可以看出，考虑互惠性的算法CFRPR和CRBPR的F值都要略高于其他的推荐算法，进一步证明了互惠性在小同行推荐中的优化意义，使整体推荐效果有了明显的提高。

5.3.4 评价不同α值对推荐结果的影响

针对算法CRBPR，为了检测不同权重值条件下混合互惠性算法的性能情况，进而反映基于协同过滤的隐式互惠和基于内容的显式互惠对用户选择的影响程度，通过对α和β设置不同的值，来对比推荐成功率的高低。成功率的定义是：科研人员选择与候选人员建立小同行链接，则算成功。由于β=1-α，因此本节通过设置不同的α值来观察变化，如图8所示。可以看出，当α分别取0和1时，推荐的成功率都相对较低。这表明单纯地考虑显式互惠性或者隐式互惠性都无法全面地度量用户之间的互惠偏好，从而影响推荐的成功率。当α取0.6左右时，推荐的成功率最高，这与真实应用场景中，科研人员在选择小同行时更看重研究内容的双向匹配度相符合。

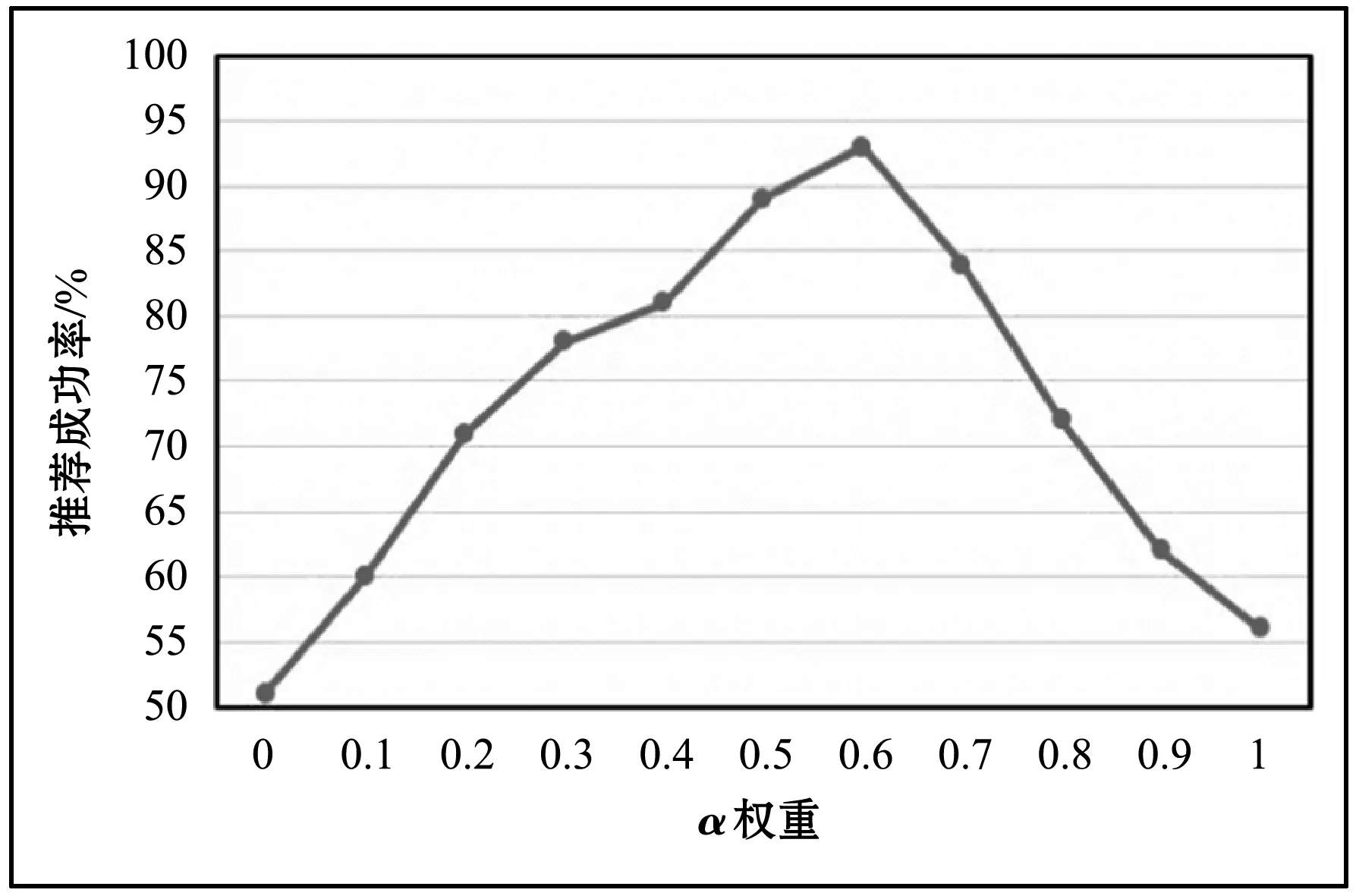
图8 权重α与推荐成功率之间的关系

5.3.5 针对冷启动问题评估本文算法

由于双向推荐是基于两个科研人员的偏好出发进行建模，针对没有任何行为记录和科研成果等内容时，双向推荐可以通过对候选人偏好赋予完全权重来实现推荐，很好地解决了冷启动问题。图9是将两个基于互惠性的双向推荐算法CFRPR和CFBPPR，与不考虑互惠性的算法MSBPR和CFBPR针对新老科研人员的推荐成功率进行比较。其中MSBPR和CFBPR在遇到新注册科研人员的冷启动问题，采用近邻科研人员的偏好相似来处理。

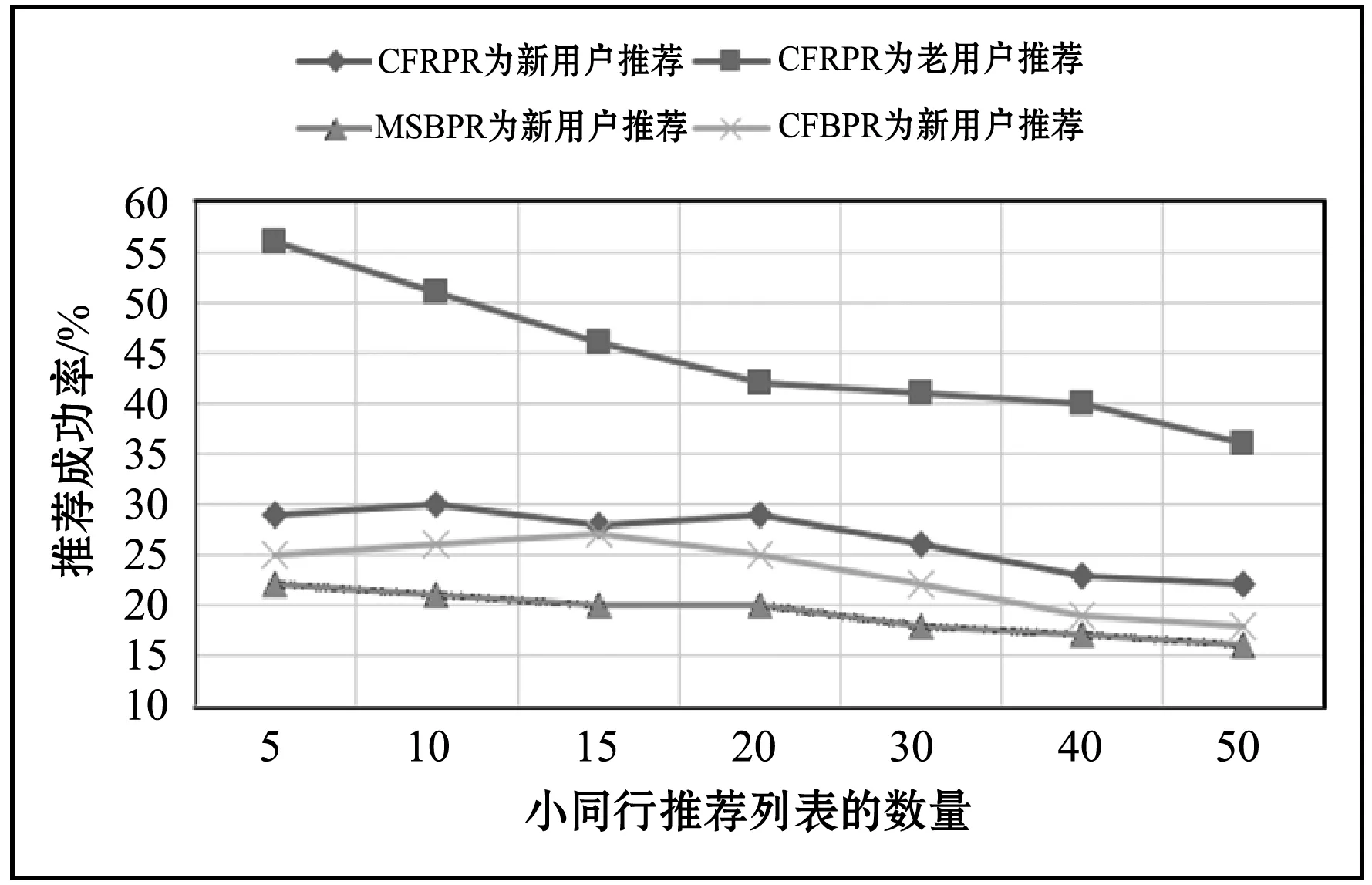
图9 新老用户推荐成功率对比

可以看出来，相对于已经在科研社区活跃一段时间的科研人员来说，为新科研人员推荐小同行的成功率普遍要低一些。这是因为新的科研人员缺少必要的信息支持，难以识别他/她无论是基于研究方向还是历史行为的偏好。但与传统的基于的推荐方法相比，针对同一组新注册的科研人员，双向推荐的成功率有了一定程度的提高。例如图中的TOP10推荐，双向推荐小同行的成功率大约可以达到30%左右，这是由于通过考虑候选科研人员的偏好，相比传统地通过近邻用户的偏好来近似处理的方法，能够尽可能地过滤出互惠的推荐，提高推荐的成功率。

5.3.6 其他实验探索

通过基于不同实验视角的对比，也发现了一些其他有趣的事实。在实验中将使用小同行推荐服务的科研人员分为两组：

1) 成功推荐组SR：推荐算法至少向其推荐了一位成功建立小同行双向链接的科研人员；

2) 未成功推荐组UR：所有其他使用小同行推荐服务的科研人员。

根据t检验结果，SR组中的所有科研人员都比UR组中的科研人员发送了更多的好友请求(平均每个用户发送的信息数为47.7 vs 28.9)。这也是协同过滤推荐的特点——科研人员更活跃地与他人联系，推荐系统就能够获取更多关于其品味和吸引力的信息，推荐因此会更有效。

此外，所有模型在基于IC的基准下对于较年轻的科研人员表现得更好，而较年长的科研人员则在基于RC的基准下有更好的性能表现。这是因为年长科研人员普遍来说相比年轻科研人员更少主动发起链接请求，因此能够获取到关于其行为偏好的信息更少，从而导致较差的基于IC基准的表现。然而，可能因为年长科研人员的科研成果较多，当其要与科研人员建立小同行联系时，得到回复的概率更大(41.7% vs 年轻科研人员的21.4%)。因此通过这些双向联系仍然能够捕获他/她们的吸引力，从而获得与年轻科研人员相近的基于RC基准的表现。

6 结 语

小同行推荐的应用场景本质上是用户到用户的推荐，参与的双方既是使用推荐服务的用户，又是待推荐用户。他们不仅在研究兴趣偏好和行为偏好上相似，而且双方的偏好都需要得到满足，达到互惠的推荐效果。针对这种特征，本文提出了一种基于互惠性的双向推荐方法。分别从基于协同过滤的角度以及融合基于内容的互惠相似性进行候选列表的过滤筛选。与传统的推荐方法相比，可以很好地解决推荐系统中新用户存在的冷启动问题，同时能提高小同行匹配的成功率，从而优化推荐的效果。

由于双向推荐是一个新兴的研究热点，所以本文的研究还有待于进一步地深入完善。通过加入一些敏感性分析(例如改变用户池、改变测试/训练的时间段等)来进一步提高混合模型的效果和鲁棒性。另外，由于本文主要针对科研社交网络中的小同行推荐研究，如何将该推荐方法完善优化，以应用到其他领域基于互惠性的推荐问题中，例如高校申请网络(高校学生和高校作为节点)、求职网络(求职者和招聘单位作为节点)等，将是下一步的研究重点。