基于卷积神经网络和近红外光谱的土壤有机碳预测模型

史 杨 王儒敬 汪玉冰

1(中国科学院合肥智能机械研究所 安徽 合肥 230031)2(中国科学技术大学自动化系 安徽 合肥 230027)

0 引 言

土壤成分信息对研究农田资源管理、精准施肥、土壤肥力分布都具有重要的意义，目前常采用实验室分析的方法获取。实验室分析方法分析结果虽然很精确，但是由于需要进行复杂的操作，所需时间和经济成本较高，并且很难实现田间原位的快速测量，难以得到大规模的应用[1]。近红外光谱分析技术通过测量样品的光谱信息，建立样品光谱和样品成分的校正模型，可以预测未知样品的成分信息[2]。近红外光谱分析是一种间接获取样品成分信息的技术，具有非接触式检测、低成本等优点，很多研究人员尝试将其用于土壤信息的快速获取，并取得一些成效。目前，近红外光谱分析技术已应用在土壤的质地分类[3]、含水量预测[4-5]、氮素含量预测[6-8]、有机质含量预测[9]等方面。

由于近红外光谱分析方法是一种间接获取信息的手段，建立有效的土壤样本光谱与成分信息之间的校正模型至关重要。校正模型一般使用化学计量学方法建立，其效果直接影响预测的可行性与准确性[10]。过去，在基于近红外光谱的土壤成分预测分析建模中，常采用多元线性回归MLR(Multiple Linear Regression)、主成分回归PCR(Principle Component Regression)、偏最小二乘回归PLSR(Partial Least Squares Regression)等线性回归方法。光谱数据通常维度高，不同波长的吸收率或反射率之间存在多重相关性，所以建模时需要采用波长选择或特征表示的方法降低维数。波长选择方法依赖对目标成分敏感波段的先验知识或基于统计方法对各波长的重要程度评估结果，从原始全谱中挑选出部分有用波段的数据进行回归计算[11]。特征表示的方法一般对全谱数据进行空间的转换，寻找在其他空间的、更易于回归计算的数据表示。例如，基于PCR或PLSR的模型使用线性变换提取出全谱数据的主成分进行特征表示和数据降维，Vohland等[12]利用连续小波变换对光谱数据进行特征表示。获得光谱数据的特征表示后，再使用回归方法对土壤中的目标成分进行预测，其中最简单的形式是线性回归预测。近年来，支持向量回归SVR(Support Vector Regression)、随机森林、神经网络等机器学习中的一些技术也被应用到光谱分析中来提升模型预测能力[13-15]。在土壤差异性较大的大面积土壤成分预测应用中一般采用局部建模方法[16]，即从大规模光谱数据库中选出与目标样本相似的样本，再利用选出的样本建模。在目前的研究中，特征表示与回归预测通常是分离的，并且较多采用了线性方法，非线性模型在光谱分析中应用的研究较少。深度卷积神经网络是一种非线性模型，是近些年机器学习研究的热点，已被成功应用在图像目标识别、自然语言处理等多个领域。深度卷积神经网络模型包含多层级非线性变换，将特征表示和回归预测统一起来，善于从大量原始数据中自动抽取有用的特征表示，在特征提取和建模上与浅层模型、线性方法相比具有明显的优势[17]。然而目前深度卷积神经网络在光谱分析预测建模方面应用的研究目前较少。

本文提出将卷积深度神经网络用于建立土壤近红外光谱和土壤成分的模型中，即构建一个多层前馈卷积神经网络模型，以土壤近红外光谱作为输入，以需要预测的土壤成分含量作为输出，实现通过测量土壤样品近红外光谱，准确预测土壤成分的目标。实验证明，利用近红外光谱预测土壤中有机碳含量具有可行性；使用包含6～7个卷积层的深度卷积神经网络模型预测有机碳含量的均方根误差可以达到9.69 g/kg，比其他线性建模方法预测大尺度土壤有机碳更准确。

1 深度卷积神经网络

1.1 前馈神经网络

神经网络的基本组成单元是神经元，一般为多输入单输出的结构，模型如图1所示。神经元分为两部分，第一部分为输入信号的加权和函数，第二部分为非线性激活单元，称为神经元的激活函数，输入与输出之间的关系可用下式表示：

(1)

(2)

式中，X=[x1,x2,…]表示神经元接受的多维输入信号，W=[w1,w2,…]表示输入信号对应的权重，b为神经元的偏置项，z为神经元输入的加权和，a为神经元输出。f(·)为神经元的激活函数，通常采用非线性函数实现，如S型函数(sigmoid)、双曲正切函数(tanh)、修正线性单元ReLU(Rectified Linear Unit)函数等。

图1 神经元模型

多层感知器是一种典型的前馈神经网络，由一个输入层、一个或多个隐含层以及一个输出层级联组合而成。图2为包含两个隐含层的多层感知器模型的结构，多层感知器的隐含层、输出层均为全连接层，每个全连接层包含多个神经元，同一层级中的各个神经元都接受前一层所有神经元的输出作为输入，同一层级的神经元之间没有连接。与多层感知器类似，每个神经元只与前一层的神经元相连，接受其作为输入并输出到下一层，各层间没有反馈的神经网络称为前馈神经网络。多层感知器模型在实际应用时一般采用不超过三层的浅层网络。

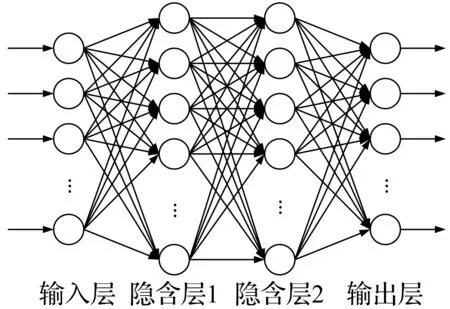
图2 多层感知器结构

1.2 卷积神经网络

卷积神经网络是指在前馈神经网络结构中使用了一个或多个卷积层。卷积层中，各个神经元通过卷积核与前一层输出的局部区域相连，生成多个特征映射面。图3为尺寸为3，步长为1的一维卷积核以类似滑动窗口的方式与输入信号进行一维卷积运算，将7维输入信号卷积生成一个5维的特征映射面。一个特征映射面尽管包含多维输出，但是各个神经元使用的为同一个卷积核，因此需要训练的参数与神经元个数无关，仅与卷积核的大小有关。如图3中的特征映射面生成所示，虽然有5个神经元输出，但是需要训练的参数只有3+1=4个，其中3是卷积核大小，1为偏置项。如果特征映射面中的5个神经元都以全连接的方式与前一层相连，需要训练的参数个数则为5×(7+1)=40个。卷积层的策略被称为权值共享，与全连接层相比，能大大减少训练参数个数[17]。利用卷积层的堆叠，可以在不显著增加模型训练参数的前提下，实现更深的网络结构。

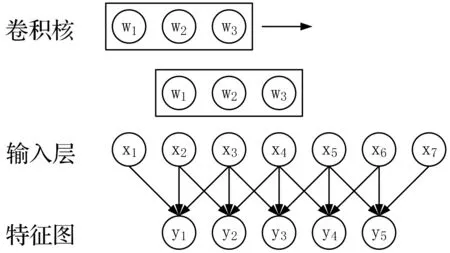
图3 一维卷积核与特征图

1.3 卷积神经网络的训练

利用土壤光谱预测成分含量模型的输入为光谱信号，输出为成分含量。在使用卷积神经网络模型时，将数据集中光谱各波长的数值进行了归一化处理后再作为模型的输入。由于预测成分含量是回归问题，采用了均方误差作为神经网络模型的代价函数，如下式所示：

(3)

式中：yi，predict和yi，real分别为第i个样本的预测输出值与实验室分析测得数值，样本集一共包含N个样本。代价函数计算得到的数值越小，表示在这个集合上，神经网络拟合效果越好。对神经网络的训练也是为了降低代价函数计算的数值。

求解神经网络代价函数的最小值常采用反向传播算法。反向传播算法建立在梯度下降法的基础上，可以用来对多层前馈神经网络进行训练。反向传播算法由正向传播过程和反向传播过程两部分组成。在卷积神经网络模型训练的正向传播过程中，输入样本正向依次经过网络各层计算后得到成分含量的预测输出。将输出与实验室测量的数值(监督信息)进行比对后，进行代价函数的计算，计算的代价将作为反向传播过程修改神经网络各层参数的依据。传统的梯度下降法中，更新参数依据下式：

θt=θt-1-η·gt

(4)

gt=▽θt-1f(θt-1)

(5)

式中：θ为神经网络模型中各神经元的参数，包含神经元的权值与偏置，由于权值与偏置更新规则相似，因此统一以参数θ表示；η为学习率，每次迭代时，各参数都在梯度方向gt以固定的学习率进行更新。反向传播过程中，由输出层向输入层方向逐层计算梯度，逐层更新各层神经元参数。

在训练模型时，如果采用固定的学习率，较小的学习率会造成训练速度很慢，而较大的学习率会造成训练后期在最小值附近来回震荡。Adagrad方法[18]对学习率进行了改进，改进后的参数更新规则如下：

(6)

(7)

式中：nt为训练过程中的梯度累积项，更新规则中加入后相当于采用了逐渐减小的学习率，避免了固定学习率设置不当的问题。

2 实 验

2.1 LUCAS土壤数据集及处理

2008年-2012年间，欧盟开展了欧洲土地利用及覆盖统计调查LUCAS(European Land Use/Cover Area frame Statistical Survey)，在此期间收集测试了大量土壤样本，样本采样点遍及欧洲23个国家，包含耕地、草地、林地等用地类型，土壤样本差异性较大[19-20]。调查前，调查部门对土壤样本取样点进行了总体规划，并对取样方式进行了一致性规范；取样后对其理化特性进行测试和可见近红外光谱的测量。土壤样本的理化特性分析均由ISO认证的实验室完成。

LUCAS数据集中包含矿质土样共17 272个。土壤样本的有机碳含量依据ISO 10694-1995干烧方法进行测量，数据集中基本信息统计见表1。测量近红外光谱前，将土壤样本进行风干、过筛预处理，再使用FOSS XDS近红外光谱分析仪进行测量。

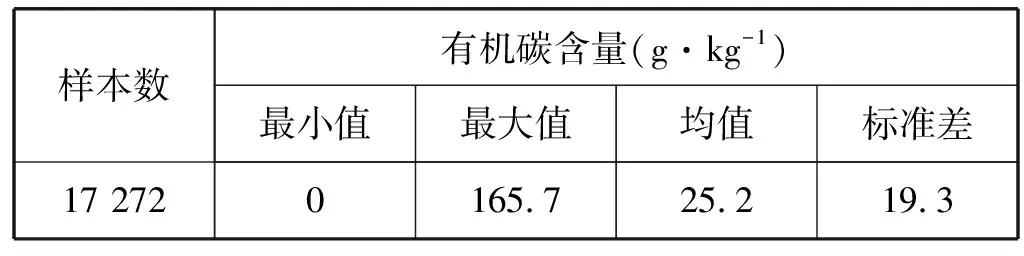
表1 LUCAS土壤数据集基本信息

由于LUCAS土壤数据库包含的样本量较多，我们将数据库中包含的17 272个土壤样本划分为建模集、验证集、测试集，三个集合中的土壤样本独立不交叉。数据库中随机选出15 000个样本作为建模集，用来对模型进行训练；再从剩余的样本里随机选出1 000个样本作为验证集，用来辅助确定模型的参数，不直接参与训练模型；最后剩余的1 272个样本作为测试集，用来评价最终建模效果。

光谱仪测量波长范围为400～2 500 nm，波长间隔为0.5 nm，因此原始光谱中包含4 200维数据。由于光谱曲线一般比较平滑，光谱相邻波长的数值共线性较强，高分辨率会造成模型中需要训练的参数过多，因此在建模前，对近红外原始光谱进行等距降采样处理，降采样后的光谱包含420维数据，波长间隔为5 nm。

2.2 深度卷积神经网络的结构

深度卷积神经网络的模型容量和表示能力可以通过设置模型的层数和各层的超参数进行调节。层数越多、各层的神经元数目越多，模型表示能力越强，同时，需要训练的参数更多，一般来说对训练集的样本量需求更大，否则在训练时容易出现过拟合现象。

本文设计了五种深度卷积神经网络的结构，分别以其包含的卷积层的层数命名为CNN-3～CNN-7，五种卷积神经网络模型的详细参数见表2。如表2第二列所示，CNN-3模型中土壤光谱信号自上而下依次经过三个卷积层和两个全连接层，输出土壤成分的预测数值。CNN-3模型的输入为420维的光谱，第一个卷积层采用512个尺寸为7的卷积核，生成512层特征映射面；第二、三个卷积层均采用64个尺寸为3的卷积核，生成64层特征映射面；两个全连接层均包含64个神经元；输出层只有一个神经元，这个神经元的输出就是模型输出的有机碳含量的预测数值。

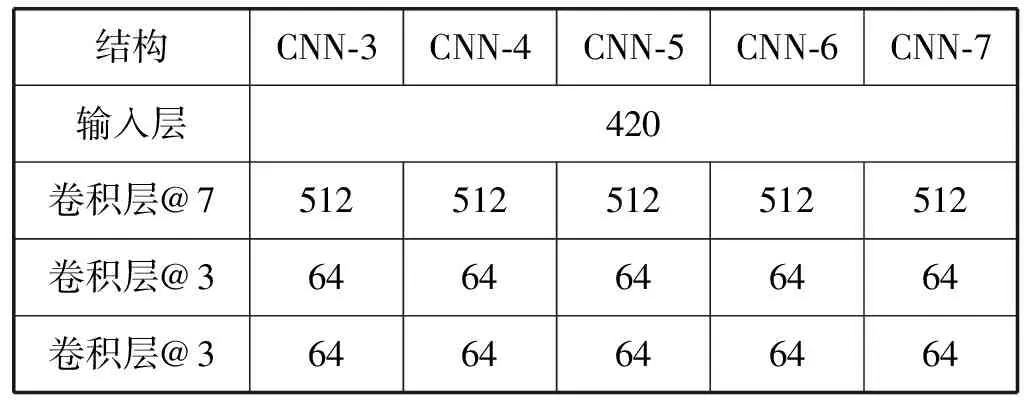
表2 五种卷积神经网络的结构

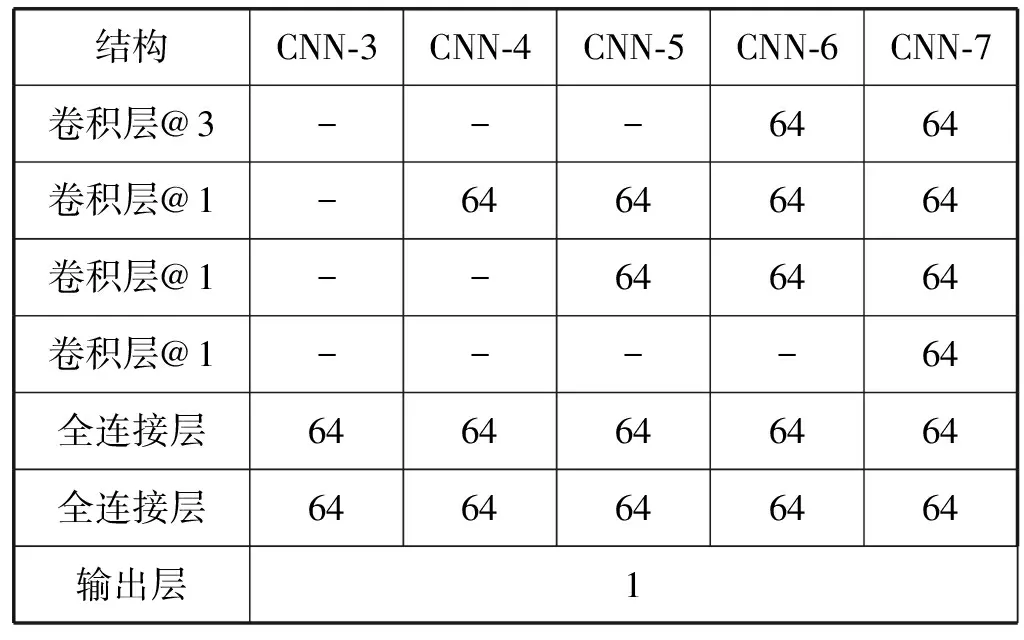
续表2

在CNN-3模型的基础上，CNN-4～CNN-7在全连接层前添加了若干个尺寸为3或1的卷积层，形成更深的卷积模型。为了避免深度网络学习过程的神经元饱和、梯度扩散现象，神经网络中各个神经元的激活函数均采用ReLU函数[21-22]。

文中深度卷积神经网络均使用Python语言调用Keras[23]工具包实现。Keras是一个深度学习计算框架，可以方便地调用显卡的并行计算能力，大大加速神经网络的训练。

3 结果与讨论

3.1 光谱曲线特征

图4是将LUCAS土壤数据库中的17 272个矿质土壤样本按照有机碳含量的25分位、50分位、75分位为分界线，分为四类不同含量等级的子集，再计算每个子集中土壤样本的平均光谱曲线。如图4所示，不同有机碳含量等级的近红外光谱均在1 400、1 900和2 200 nm左右有明显的峰值，整体光谱曲线趋势一致；有机碳含量级别越高的土壤样本的平均光谱在整个可见光近红外波段吸光度都高于有机碳含量级别较低的类别。

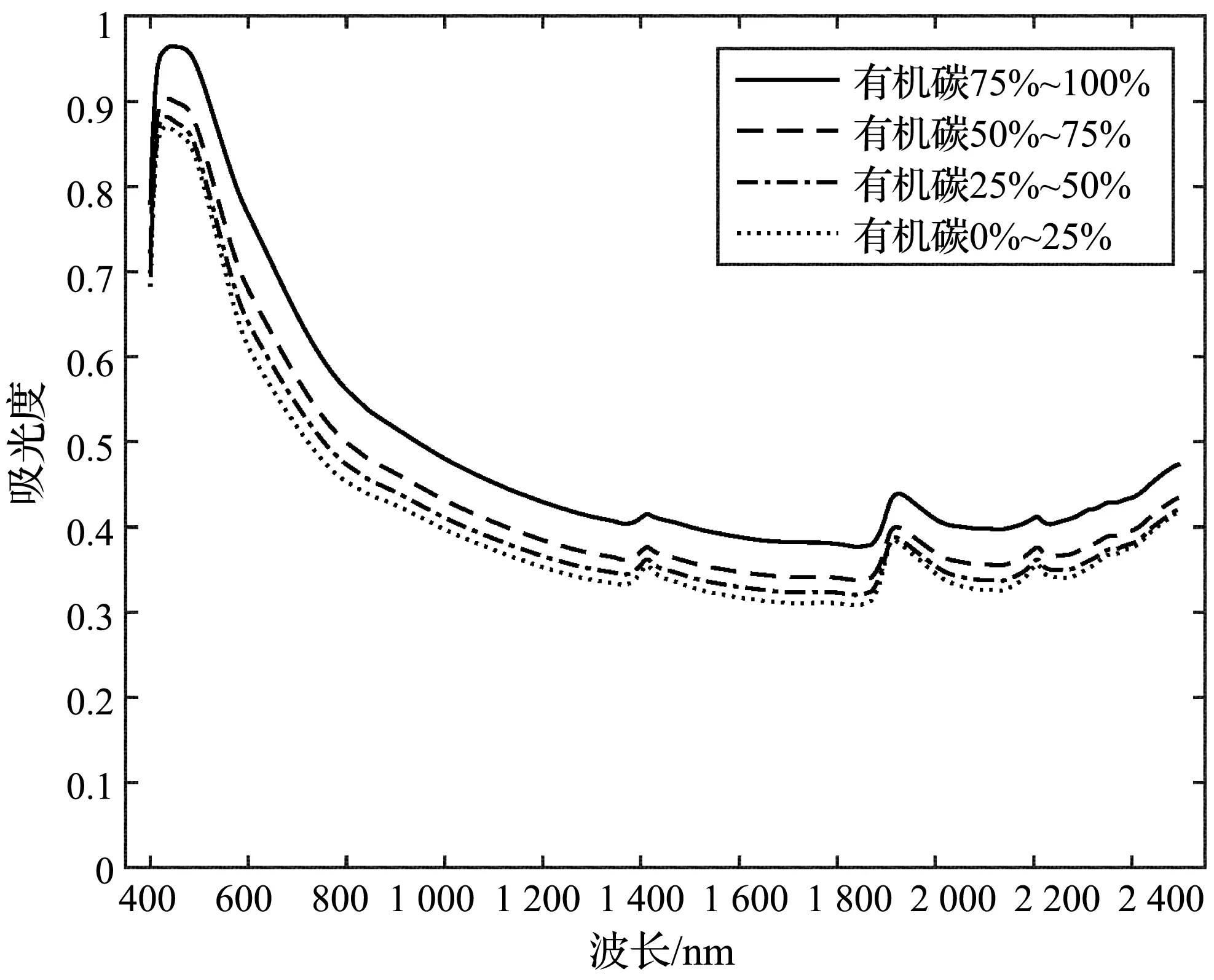
图4 不同有机碳含量的土壤样本的平均光谱

3.2 模型预测结果及评价

实验中，首先将LUCAS土壤数据库划分为建模集、验证集、测试集三个部分。然后使用表2所示的五种卷积神经网络模型分别建立土壤有机碳含量及近红外光谱的校正模型，模型参数调节时只使用建模集。最后利用建好的模型，根据测试集中土壤样本的近红外光谱，预测样本的有机碳含量。为了更好地了解卷积神经网络模型的效果，实现了PCR和PCA+SVR两个线性模型作对比。其中，PCR模型采用了40个主成分参与线性回归计算；PCA+SVR中先使用PCA方法提取40个主成分后，使用SVR线性回归模型进行土壤有机碳含量的预测。图5-图9分别为CNN-3～CNN-7五个模型预测值与实验室方法测量数值的散点图，图10为PCR模型的预测结果。如图5～10所示，六个模型建模效果良好，散点比较均匀地分布在回归直线两侧，呈正相关关系；CNN-6、CNN-7两个模型在有机碳含量较低区域比其他模型更集中在回归直线两侧。因此，利用土壤的近红外光谱间接预测土壤有机碳含量是可行的。

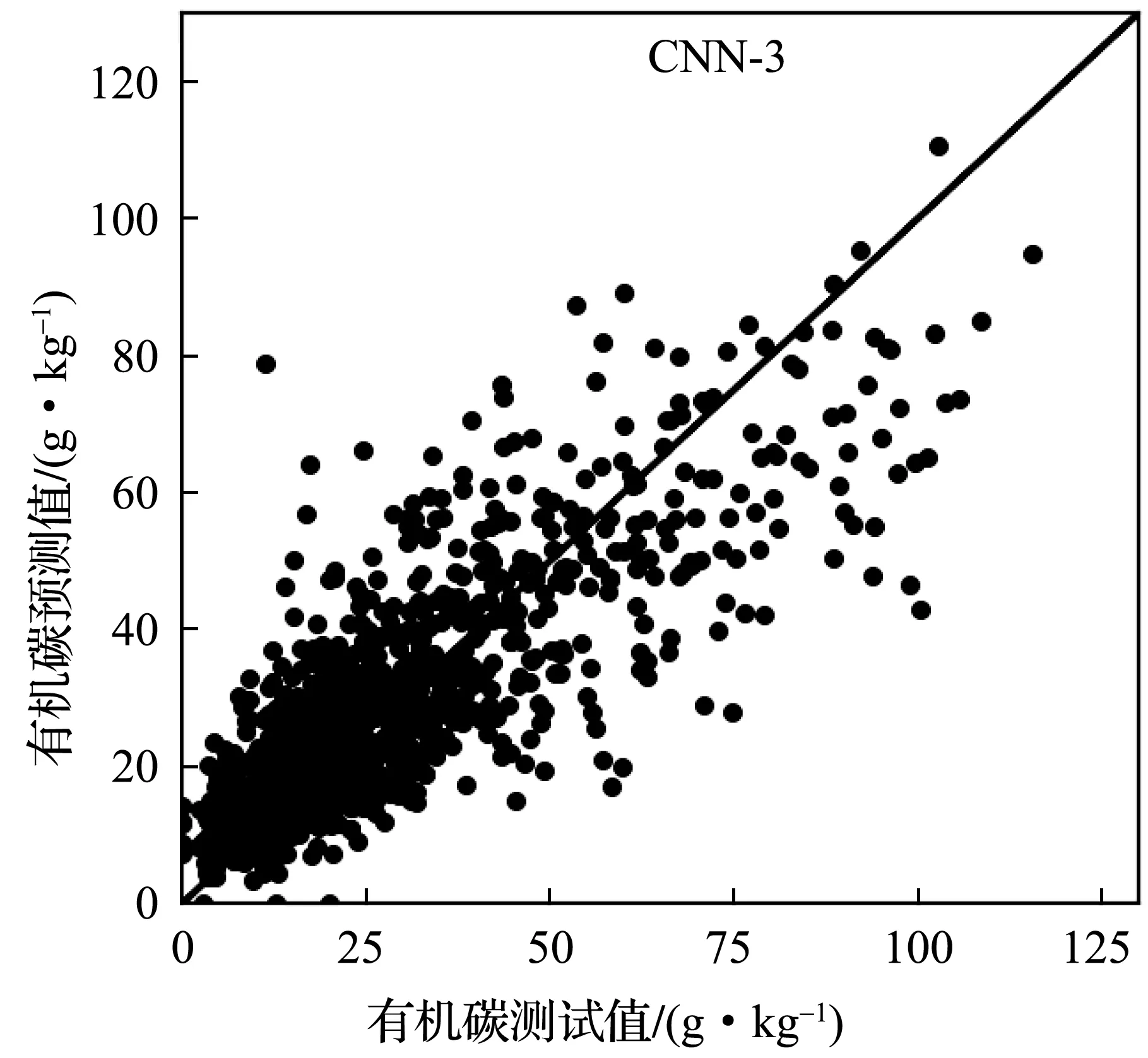
图5 CNN-3模型在测试集上的预测结果

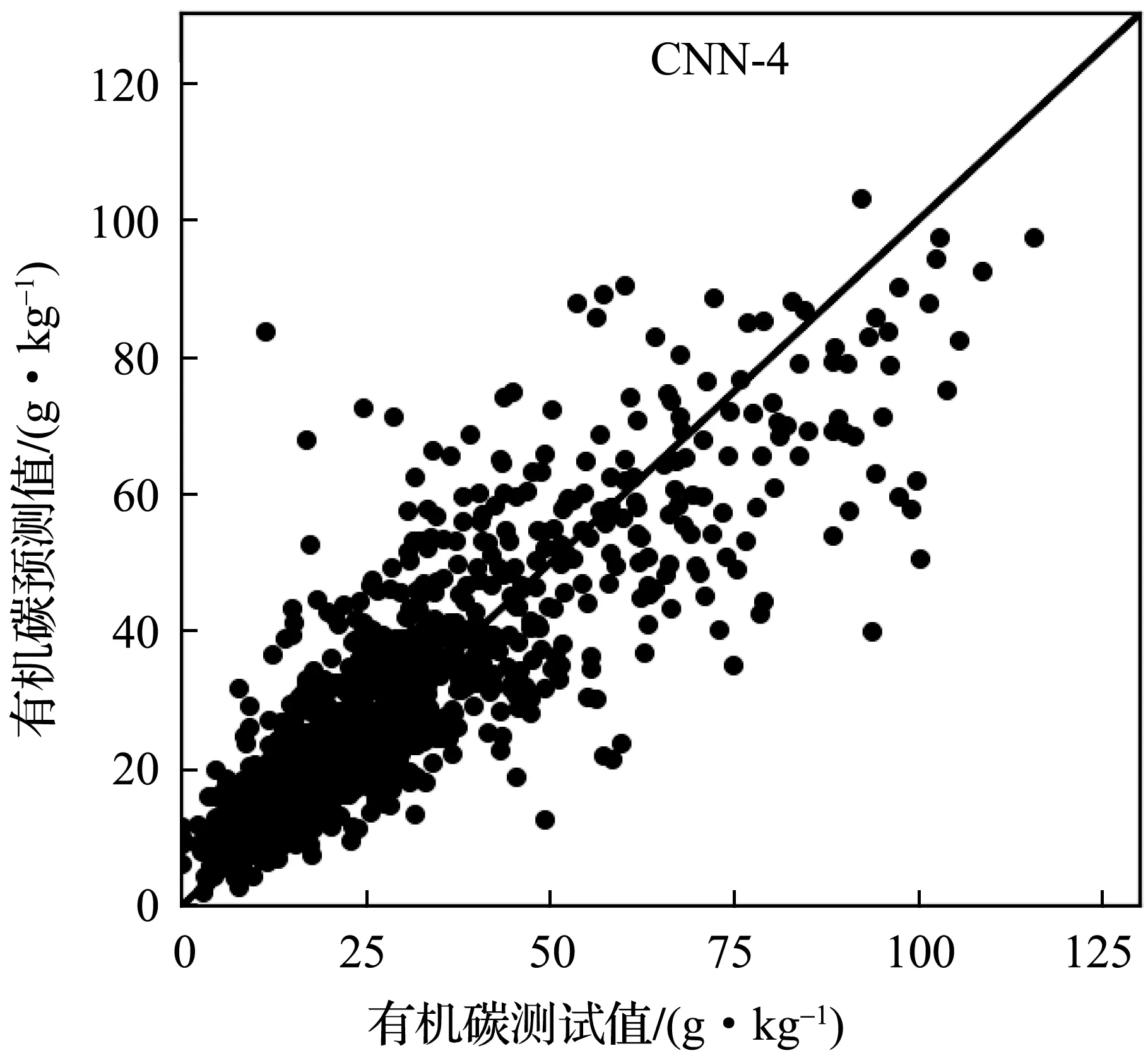
图6 CNN-4模型在测试集上的预测结果

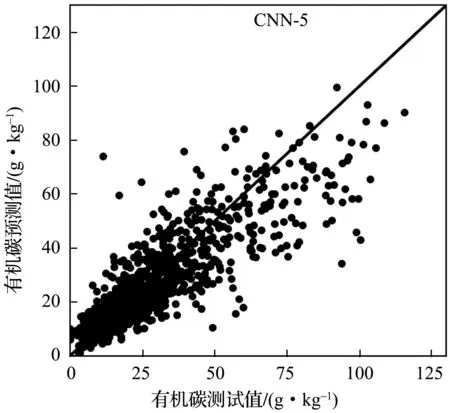
图7 CNN-5模型在测试集上的预测结果

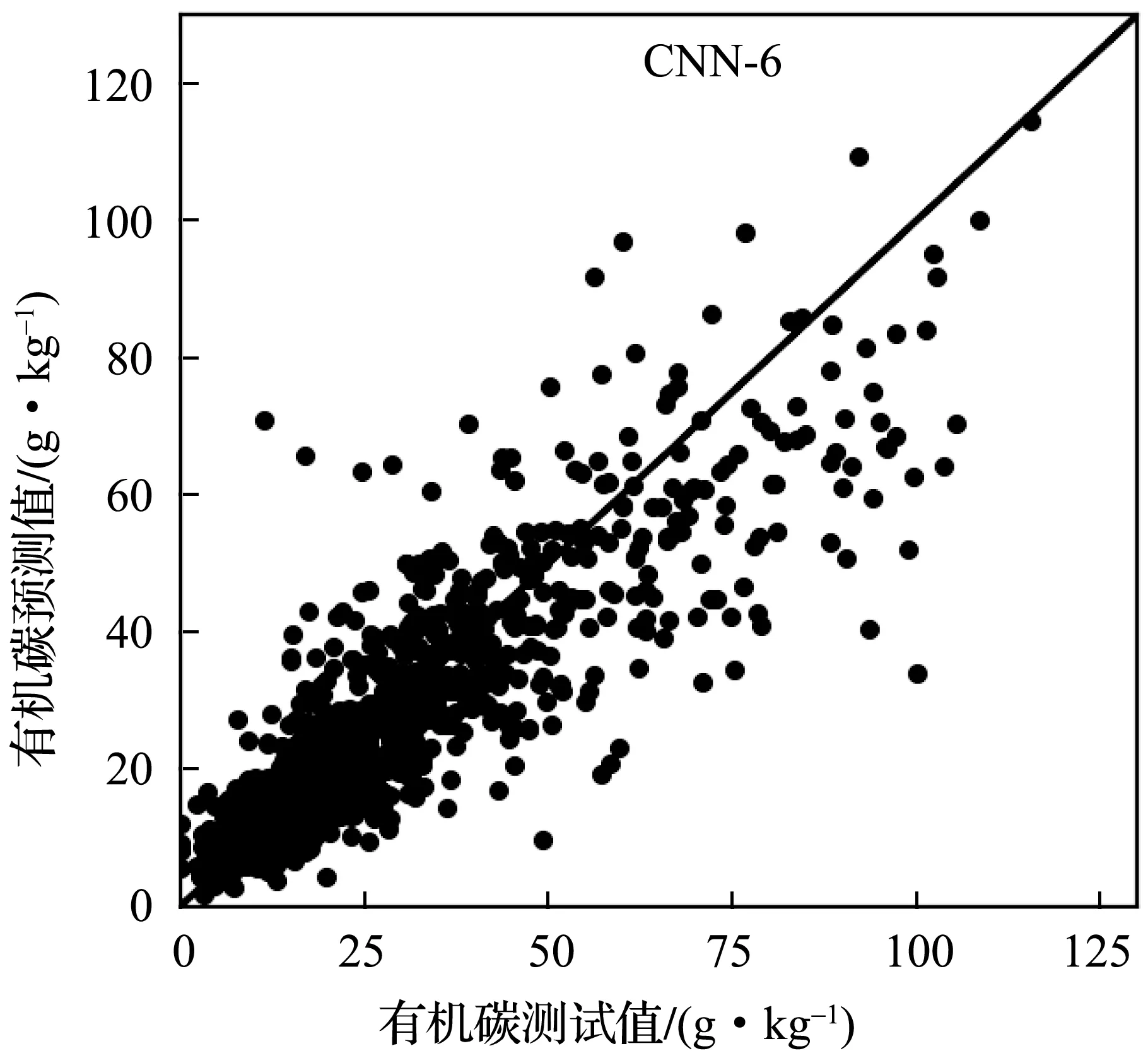
图8 CNN-6模型在测试集上的预测结果

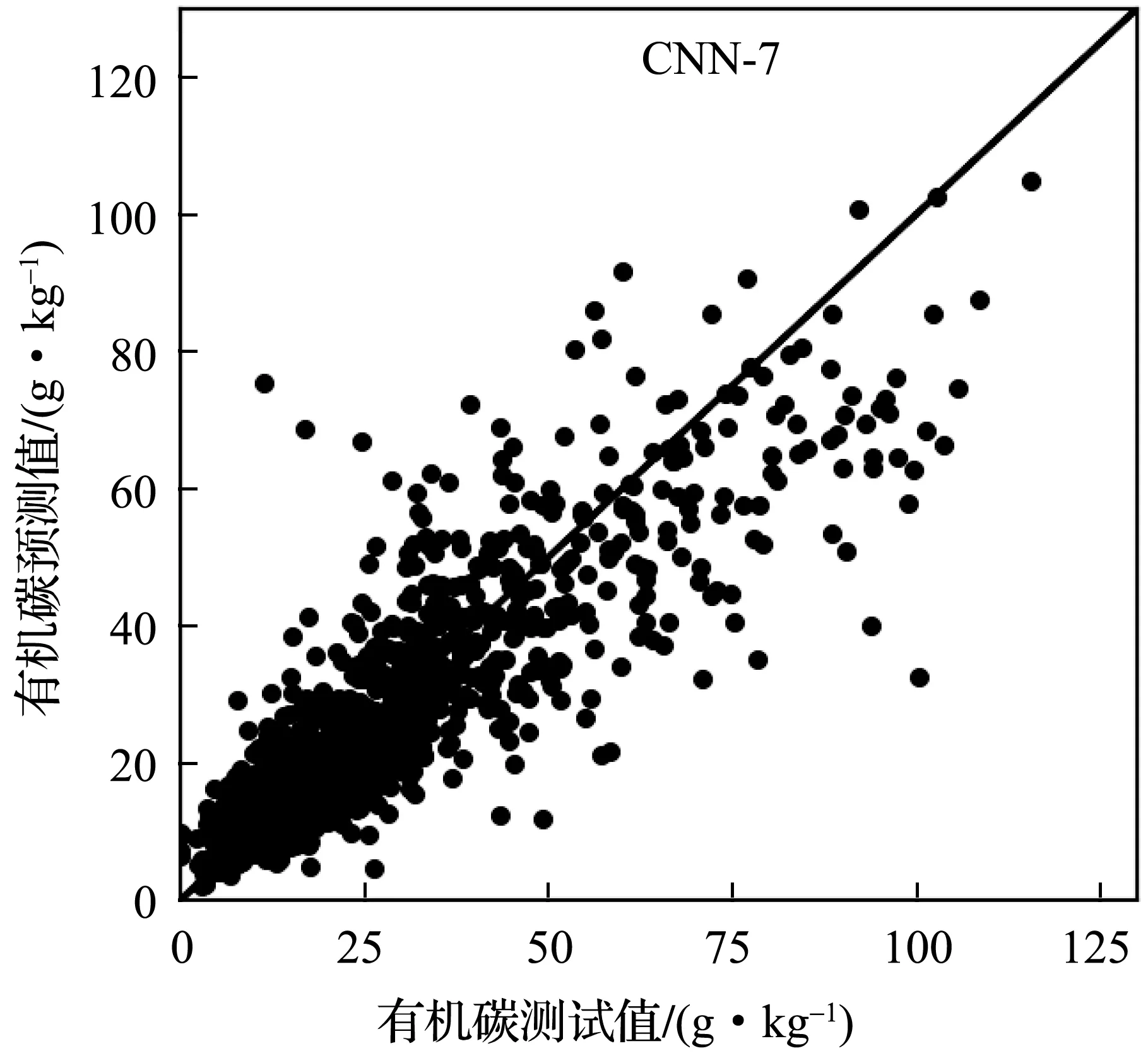
图9 CNN-7模型在测试集上的预测结果

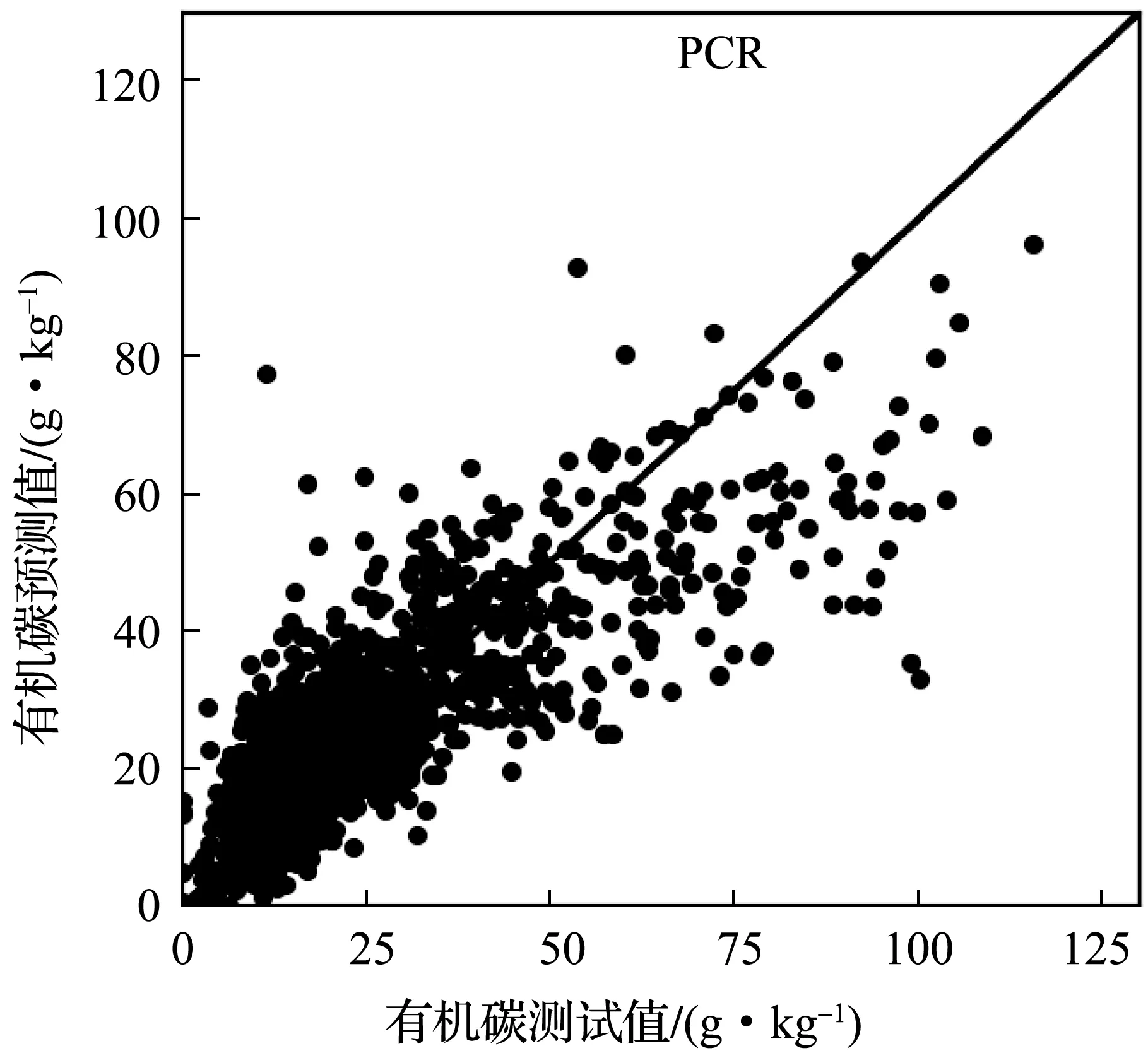
图10 PCR模型在测试集上的预测结果

回归问题对模型性能进行量化评价常采用均方根误差RMSE(Root Mean Square Error)指标，即预测值与真实值的误差平方均值的平方根。均方根误差的数值越小，表示回归模型的预测性能越好。表3为五种不同深度的卷积神经网络模型在同一划分下的建模集、验证集、测试集上的均方根误差。

表3 模型预测效果的对比

如表3所示，CNN-3～CNN-7模型在建模集、验证集、测试集上的预测效果全面优于PCR和PCA+SVR这两个线性模型；与线性模型不同，CNN模型的模型容量很大，训练时一般在建模集上会存在轻微的过拟合现象，因此预测性能要优于其在验证集和测试集上的表现，验证集和测试集的结果更能反映模型的泛化能力；随着神经网络层数的加深，在测试集上预测效果逐步提升，RMSE值从11.20 g/kg逐渐减少到9.69 g/kg；采用6个卷积层的CNN-6与采用7个卷积层的CNN-7模型效果非常接近。回归问题另外一个常用的评价指标是决定系数(R2)，决定系数越接近1，表示模型拟合效果越好。PCR模型的决定系数0.65，CNN-7模型的决定系数达到0.76，较PCR模型提升了17%。实验结果表明，使用包含6～7个卷积层的深度卷积神经网络模型成功地抽取出了比主成分更好的非线性特征，利用这些非线性特征预测有机碳含量的均方根误差可以达到9.69 g/kg，比其他线性建模方法预测大尺度土壤有机碳更准确。

4 结 语

过去利用近红外光谱预测土壤成分含量的研究多是基于单一土壤类型的、小样本的校正模型，模型结构简单，表示能力有限，难以实现大尺度、土壤种类复杂环境下的应用。本文提出的基于深度卷积神经网络的校正模型，能够应用在土壤种类繁多的欧洲大陆尺度的土壤有机碳含量的预测中。实验证明了使用包含6～7个卷积层的深度神经网络在大尺度土壤有机碳预测问题中的可行性和准确性。由于卷积神经网络容量较大，而目前可以用来训练模型的土壤样本数有限，因此对深度神经网络在土壤成分预测的研究仍不充分，有希望继续发掘深度神经网络的潜力。下一步工作的方向是研究如何获取更多的土壤样本，优化神经网络的结构与训练过程，尝试预测更多的土壤成分，提高预测精度。