基于AIS的船舶航行周期识别

赵文文 胡志华 魏 晨

(上海海事大学物流研究中心 上海 201306)

0 引 言

随着世界经济发展，海上贸易量显著增长，海上交通压力不断增加，船舶交通事故频发。欧洲安全局2017年发布的年度海上伤亡事故概况显示，在统计的16 500起海难事故中，百分之五十以上的海难事故由船舶航行导致，如船舶碰撞与触礁。分析船舶海上航行特征与轨迹周期性，是提高船舶航行安全管理水平的重要方法。船舶行船周期是一种船舶行为，基于船舶自动识别系统AIS数据识别船舶周期，对预测船舶位置、预警船舶行驶异常，具有重要实践意义。

AIS是基于船舶作业信息采集设备而构建的海上船舶数字助航系统，AIS数据广泛应用于船舶监控[1-2]、船舶防碰[3]、船舶行为预测[4]与环境保护[5-6]等方面。船载AIS数据是记录船舶航行与作业信息的大规模数据，包含船舶行为特征与航行规律[7]，分析和计算AIS数据，是研究船舶行为特点的重要方法。

船舶行为的作业特点与数值特征受到部分学者关注。文献[8]等利用隐马尔可夫模型和BAUM-WELCH算法，统计并分析船舶入港时的行为特点，确定船舶行为是否异常，对异常行为发出预警，保护港口设施和人员。文献[9]等基于港口海文地图和船舶轨迹建立船舶行为模型，分类和识别在港活动船舶。文献[10]等对通过港口周围拥挤航道的船只航行行为进行预测。文献[11]等基于动态贝叶斯网络建立船舶行为识别系统，预警港口船舶异常行为，并针对异常类型设计解决方案。在航运领域，船舶行为的研究主要集中在港口。与船舶在港口行为的研究相比，船舶航行行为的研究相对较少。因此，本文对船舶航行周期行为进行研究。

1 问题描述

船舶航线指在两个或多个港口之间，运输旅客和货物的船舶线路。船舶航线类型根据航线有效时间、运力与组织形式等标准进行划分。以航线有效时间段为依据，船舶航线可分为季节性航线和常年航线；以运力为依据，船舶航线可分为主干航线和分支航线；以组织形式为依据，船舶航线可分为直达航线与中转航线。

受到环境与航行条件影响，同一船舶在停靠港口、货物需求等因素相同的情况下，其航线也会发生变化。此外，港口当地监管政策、港口作业人员行为以及水路特征等因素均会影响船舶行为[12]。因此，有效识别船舶周期，有利于分析船舶行为特点，为掌握船舶航行规律、预警船舶异常行为、改进助航设备以及管理船舶交通提供帮助。

船舶AIS提供船舶静态数据、船舶动态数据和船舶航程数据。船舶静态数据包括船名、呼号、MMSI、IMO、船舶类型、船长和船宽等；船舶动态数据包括经度、纬度、船首向、航迹向和航速等；船舶航程数据包括船舶状态、吃水和目的地等。其中，船舶动态数据是船舶位置经纬数据的主要来源。本文基于船舶AIS数据中的经纬度数据，对船舶周期行为进行识别。

船舶航行轨迹是经度与纬度的有序集合，表示为公式所示：

U={(λ1,φ1),…,(λn,φn),…,(λN,φN)}

(1)

式中:U为船舶轨迹点集合；N为船舶轨迹序列长度，表示在轨迹段U中，共有N个船舶轨迹点，n=1,2,…,N；λn为第n个船舶轨迹点的经度；φn为第n个船舶轨迹点的纬度。

2 数学模型

2.1 数据预处理

AIS数据在传输过程中，信号可能受到多种因素的干扰，如河岸和建筑物的遮挡、基站信号不稳定或周围其他船舶信号的干扰等。在这些情况下，信息传输很容易出现错误，因此首先对原始数据进行清洗。结合文献[13]等在对内河航道船舶轨迹进行恢复时清洗AIS数据的方法，本文从剔除重复数据、剔除范围异常数据、剔除船舶速度异常数据和剔除船舶航向异常数据四个方面对AIS数据进行清洗。

2.1.1 剔除重复数据

船舶两个连续轨迹点A(λn,φn)和点B(λn+1,φn+1)，计算两轨迹点间距离,计算方法如下[14]：

δn= 111 199[(φn-φn+1)2+(λn-λn+1)2·

(2)

式中:δn表示第n个与第n+1个船舶轨迹点间的距离，单位为m；λ表示经度；φ表示纬度。

由式(2)可知，δn=0的唯一条件是λn=λn+1且φn=φn+1。因此，剔除重复数据的主要思想如下：首先比较第一个船舶轨迹点和第二个船舶轨迹点是否为重复轨迹点，利用式(2)得到δn，判断δn是否等于0。若δn=0，说明两个轨迹点经纬度数据相同，此时剔除第二个轨迹点；若δn≠0，则两个轨迹点均保留。相同方法对两两轨迹点间的距离进行判断，直到遍历完所有经纬度数据组。

2.1.2 剔除范围异常数据

假设船舶某轨迹点(λn,φn)，船舶航行经度范围为[λmin,λmax]，纬度范围为[φmin,φmax]，若船舶轨迹点坐标符合规则式(3)中的任意一条，则将其作为范围异常数据剔除。

λn<λmin
φn<φmin
λn>λmax
φn>φmax

(3)

式中:λmin、φmin表示经纬度范围的最小值，λmax、φmax表示经纬度范围的最大值。

2.1.3 剔除船舶速度异常数据

式(2)给出了计算船舶两轨迹点间距离的方法，两轨迹点间船舶速度计算式如下[14]：

(4)

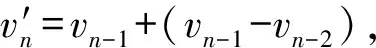
Input: 船舶轨迹点、速度及预测速度集合

m=1;

whilem<=n

V(m,:)=[ ];

else

m=m+1;

end

end

2.1.4 剔除船舶航向异常数据

已知船舶三个连续轨迹点M(λ1,φ1)、N(λ2,φ2)、P(λ3,φ3)，船舶航向变化如图1所示，∠γ为船舶从M点到N点的航向变化角，∠γ的求解过程如图1所示。

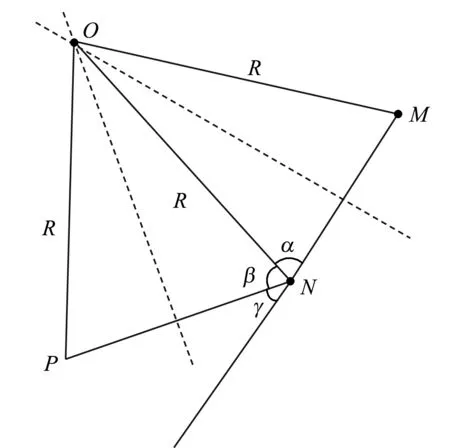
图1 船舶航向变化示意图

步骤1求出由点M、N、P确定的唯一圆心O的坐标。分别作线段MN和NP的中垂线，相交得到点O，假设点O的坐标为(λx,φx)，得到方程组如下：

(5)

对方程组进行求解，得到λx和φx如下：

(6)

式中：A=φ12-λ22-λ12-φ22,B=φ22+λ32-λ22-φ32。

步骤2假设船舶以速度v1完成整个圆周运动所用时间为T1，以速度v2完成整个圆周运动所用时间为T2。v1表示船舶经过M、N两点间的速度，v2表示船舶经过N、P两点间的速度，R表示圆周半径。T1、T2的表示方式如下：

(7)

步骤3∠γ的求解公式如下：

(8)

利用2.1.3节中确定阈值εn和剔除速度异常点的方法，确定阈值θn，从而对船舶航向异常点进行剔除。

2.2 识别船舶航行周期

2.2.1 确定港口点

寻找可能的港口位置，应从时间和速度两个方面来考虑。首先，若船舶在一个地方停靠时间较长，此处就有可能是港口，因此要对船舶停靠时间进行合理假设。其次，船舶停靠在港口时理论上应静止不动，但由于受到风、浪、流的联合作用，船舶会有极小范围的速度变化。符合以上两个条件的位置点可初步认为是港口所在地。

(1) 船舶在港时间 由于该船舶所装货物类型、吨位等具体信息未知，且船舶在港总停泊时间中包含了自然因素停泊时间等不可预知的时间，因此在对船舶在港时间进行合理假设。

船舶在港口中的主要作业为装卸作业。经试验，假设该船舶平均装卸货物为6 000吨，船舶平均每装卸千吨货在港停泊时间为0.25天，则船舶装卸作业时间T装=0.25×6=1.5(天)。式中，T装代表船舶装卸作业时间。考虑到非生产性停泊、自然因素等不可预知因素，初步确定在港总停泊时间至少为1.5天，即在寻找可能港口位置时，船舶在某处停泊1.5天或以上的时间时，才考虑该处为港口所在位置。

(2) 船舶在港速度 船舶停泊时，理论上应静止不动。但在实际情况中，由于受到风、浪、流的联合作用，船舶将发生横荡、纵荡、垂荡、横摇等六个自由度方向的运动，在这种情况下，假设船舶在港速度为1×10-3m/s左右。

符合以上两个条件的位置初步认为是港口所在地，将所选取位置的经纬度输入Google earth中进行验证和调整，得到港口点集合。假设得到的港口点集合为:

Z={(λa,φa),(λb,φb),(λc,φc)}

已知船舶航行轨迹为U={(λ1,φ1),…,(λn,φn),…,(λN,φN)}，此时船舶各段子轨迹的表示方式如下：

(9)

2.2.2 识别船舶航行周期

利用轨迹相似性来识别船舶航行周期。在判定轨迹相似性的研究中，欧式距离是度量相似性的经典方法[15]，但其只能应用于轨迹长度相等的情况，且未考虑到轨迹中的每一个特征点；DTW距离适用于求解连续时间序列的相似性；Hausdorff距离没有考虑到曲线走势[16]。船舶分段子轨迹长度不一，且数据为离散点，因此本文采用Fréchet距离法求解轨迹相似性。

Fréchet距离是法国数学家Maurice Fréchet提出的一种路径相似性描述方法。假设A、B是空间S上的两条曲线，A:[0,1]→S，B:[0,1]→S。其Fréchet距离的数学定义如下：

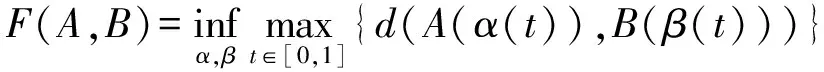
(10)

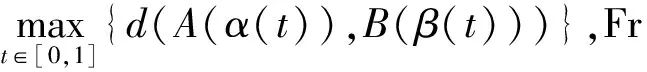
本文中，曲线A、B即为船舶任意两条子轨迹。计算船舶子轨迹的Fréchet距离，距离最小的认为两条轨迹相似，即船舶在该段航行中具有周期性。

3 算例分析

3.1 算例数据

本文以MMSI号为566906000的船舶作为研究对象，应用船舶在2014年1月15日至2014年11月18日的AIS数据对船舶航行周期进行分析识别。MMSI号即水上移动通信业务标识码(Maritime Mobile Service Identify)，是船舶无线电通信系统在其无线电信道上发送的，能独特识别各类台站和成组呼叫台站的一列九位数字码。时间戳是指格林威治时间1970年01月01日00时00分00秒(北京时间1970年01月01日08时00分00秒)起至现在的总秒数。每一组数据包括时间戳、经纬和纬度。图2所示为船舶航行轨迹图。

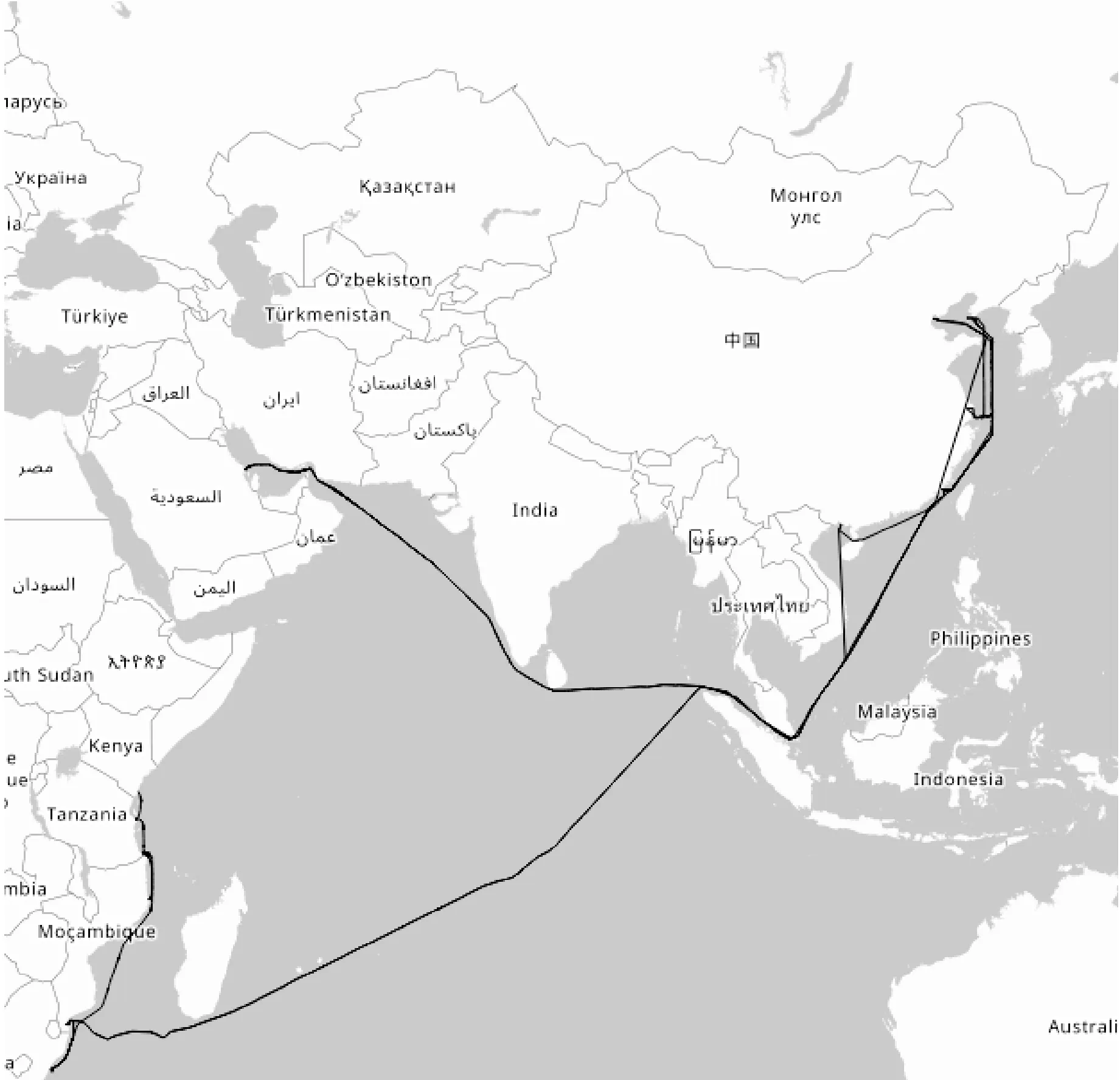
图2 船舶航行轨迹图

3.2 实验结果

(1) 确定港口点 对原始数据进行预处理后，得到船舶停靠港口点如表1所示。

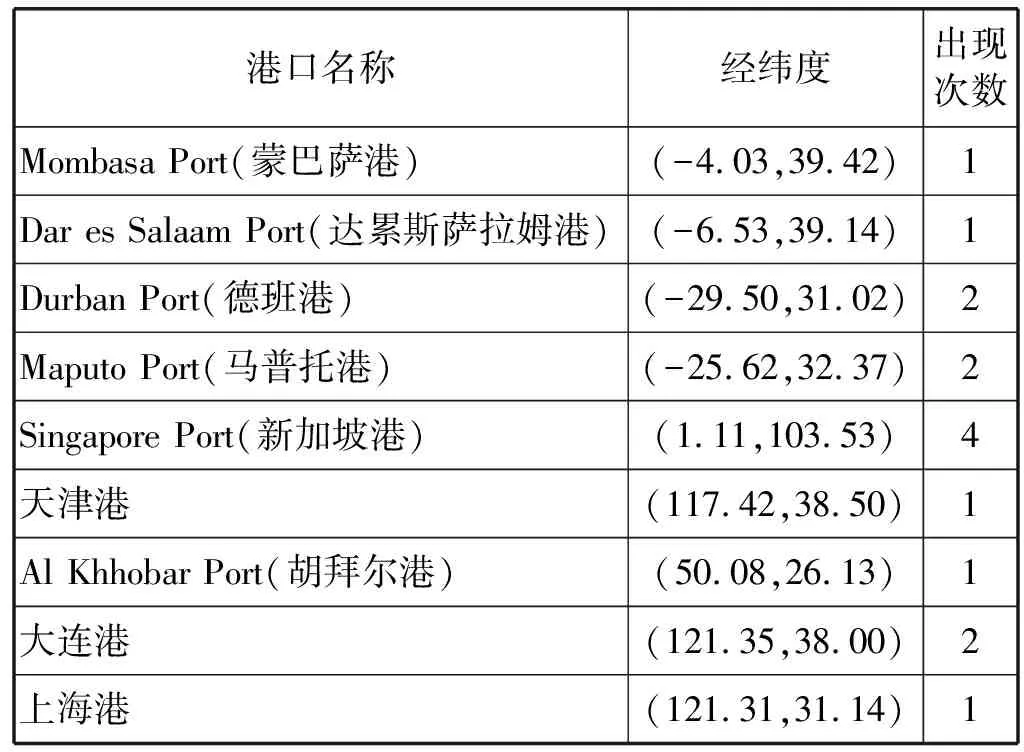
表1 船舶停靠港口点汇总

对于表中经纬度数据，经度在前，纬度在后。东经为正，西经为负；北纬为正，南纬为负。

(2) 船舶轨迹分段 由表1可知，船舶航行路线为：Mombasa Port → Dar es Salaam Port → Durban Port → Maputo Port → Singapore Port → 天津港 → Singapore Port → Al Khobar Port → Singapore Port → 大连港 → 上海港 → 大连港 → Singapore Port → Maputo Port → Durban Port。依据港口点将船舶航行轨迹分段，共分为14段子轨迹，表示方式如表2所示。

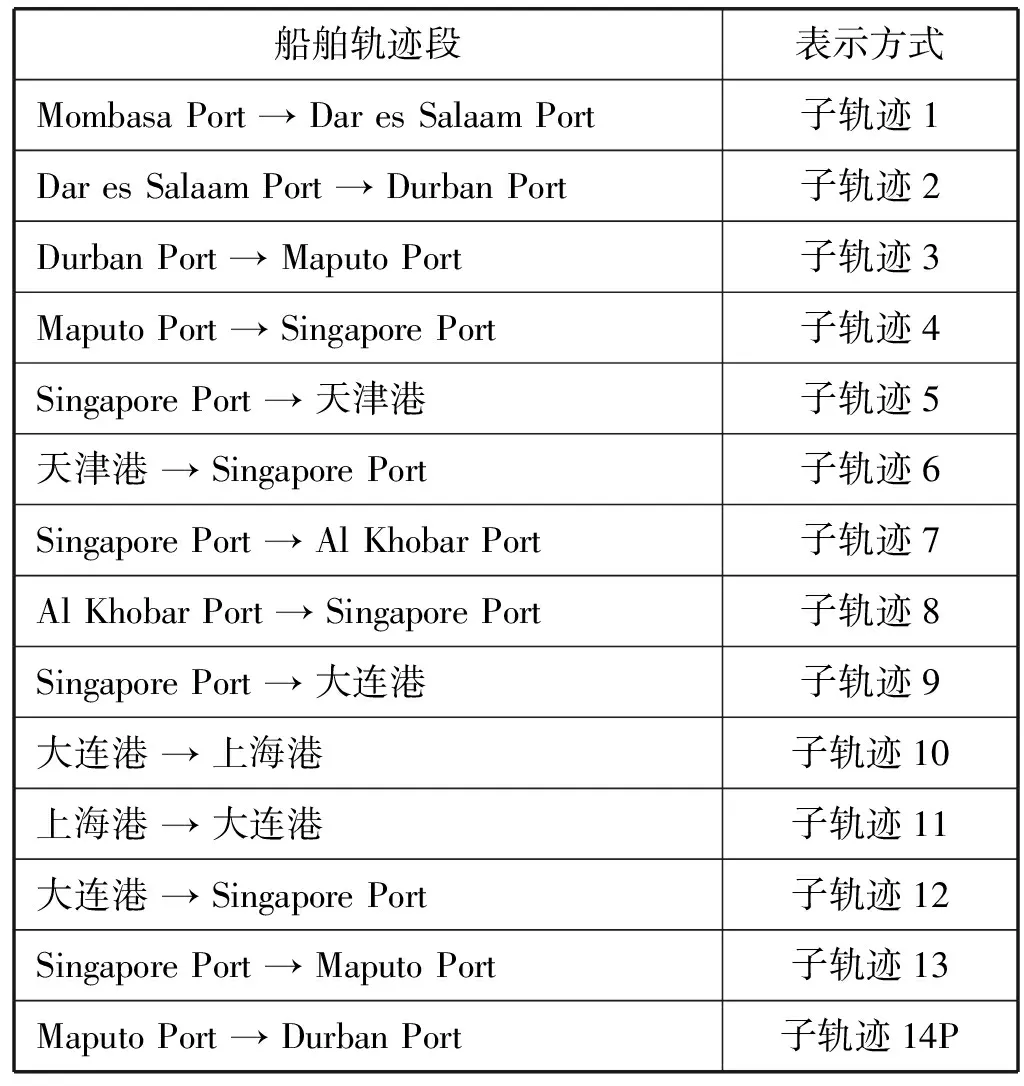
表2 船舶子轨迹表示方式

(3) 船舶子轨迹Frechet距离 船舶子轨迹Frechet距离的计算结果如表3所示。

3.3 结果比较与分析

由表4可知，子轨迹3与14、子轨迹4与13、子轨迹5与6、子轨迹7与8、子轨迹9与12以及子轨迹10与11极其相似，最终结果如表4所示。

由表4可知，2014年1月15日至2014年11月18日的航行过程中，MMSI号为566906000的船舶在德班港与马普托港，新加坡港与马普托港、天津港、胡拜尔港、大连港以及大连港与上海港之间存在航行周期。

4 结 语

以船舶308天的AIS数据为基础，对船舶航行周期进行识别。在对原始数据进行重复和异常数据的剔除后，确定出Mombasa Port(蒙巴萨港)等9个港口点，并将船舶航行轨迹分为14段子轨迹。对子轨迹进行Frechet距离的两两求解，最终得到船舶在各港口之间的周期性。结果表明，该方法可识别出船舶在不同港口间的航行周期，可行有效。

后续研究将对多条船舶的航行周期进行分析，依据航行周期可对船舶进行分类，为分析船舶行为提供进一步的理论依据。