基于多种隐式反馈数据的商品推荐算法

周巧扣 倪红军

(南京师范大学泰州学院信息工程学院 江苏 泰州 225300)

0 引 言

在推荐系统中，用户的行为记录可以分为显式反馈和隐式反馈。显式反馈是指用户对已购买商品的评分数据，通常为一段区间的整数值，例如1～5分。隐式反馈是指用户浏览记录、购买记录等，通常为二值形式，例如“0”表示未购买，“1”表示已购买。两者之间的区别在于，显式反馈反映了用户对商品的真实喜好程度，而隐式反馈表达了用户喜好存在着一定的“不确定性”。目前，大多数推荐算法都将显式反馈作为研究的对象，根据用户已有的评分数据，预测用户对其他商品的评分，根据预测评分产生商品推荐列表。例如：基于用户的近邻模型[1]、基于概率的隐语义模型[2]以及矩阵分解模型[3-4]等，然而这些算法在隐式反馈上的推荐效果并不理想。

针对隐式反馈，文献[5]提出一种面向排序的基于贝叶斯概率模型的推荐算法BPR(Bayesian Personalized Ranking)[5]。其核心思想是从用户的隐式反馈中推导出用户喜好商品的偏序对，以最优化商品排序为目标，利用偏序对训练推荐模型。该算法具有推荐内容排序精度高，易于扩展等优点，许多学者以该算法为基线进行了相关研究[6-8]。文献[6]利用用户的社交关系建立偏序对，认为与没有反馈的商品相比，用户更喜欢好友喜欢的商品，提出了一种基于用户社交关系的推荐算法。文献[7]对不同的隐式反馈进行分析，将隐式反馈分为：购买行为和浏览行为。利用不同反馈表达的不同喜好程度产生偏序关系，提出一种自适应的推荐算法。李满天等[8]提出了一种融合显式反馈和隐式反馈的面向排序的推荐算法，提升推荐算法的性能。

虽然隐式反馈在表达用户喜好时存在着“不确定性”，但比显式反馈更加丰富。例如，用户对某个商品的多次购买，可以明确表达用户对该商品的喜爱。此外，用户购买商品的时间也可以表达用户偏好的变化。本文在BPR算法的基础上，结合用户购买商品的次数和时间，提出一种基于多种隐式反馈数据的商品推荐算法MBPR(Multiple implicit feedback BPR)。利用更细粒度的偏序对训练推荐模型，进一步提高推荐算法的性能，并在真实的数据集上进行测试，验证了算法的有效性。

1 相关算法

1.1 矩阵分解模型MF(Matrix Factorization)

设有m个用户和n个商品，X∈Rm×n为用户对商品的评分矩阵。矩阵分解模型是一种隐因子模型，将X通过分解的方法映射成两个低维度矩阵的乘积，其定义如下所示：

X≈WHT

(1)

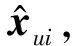
(2)

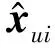
1.2 BPR算法

BPR算法采用商品偏序对的思想，其优化的目标是对商品进行正确的排序而不是对单个商品的评分。BPR算法认为用户对隐式反馈商品的偏好大于没有反馈的商品，因此为每个用户u构建一个商品的偏好序列>u，将商品偏序对作为训练数据，商品偏序对的构造过程如下：

(3)

P(Θ|>u)∝P(>u|Θ)P(Θ)

(4)

假设所有用户是相对独立的，并且每个用户u对商品(i,j)的排序与其他商品的排序相对独立，则可以将P(>u|Θ)改写为单体概率的积，如下所示：

(5)

用户u相比j更喜欢i的单体概率计算公式如下所示：

(6)

式中：σ(·)是一个logistic函数，其定义为：

(7)

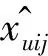
P(Θ)服从一个均值为0，方差-协方差矩阵为ΣΘ的正态分布。

P(Θ)～N(0,ΣΘ)

(8)

BPR算法的一般性优化函数如下：

(9)

式中：R(Θ)是与模型参数Θ相关的正则项。BPR算通过以上优化函数训练模型参数Θ，具体的模型可以是邻域模型或矩阵分解模型。

2 MBPR算法

2.1 扩展的偏序对

在推荐算法中，最为关键的步骤是根据用户已经购买的商品记录，分析出用户的偏好属性，然后向用户推荐用户喜欢的商品。然而，在BPR算法中，只能根据式(3)在已经购买商品和未购买商品之间产生商品偏序对，忽略了已购买商品之间的偏序关系，导致所构建的用户偏好属性不能真实反映用户的偏好，从而影响了推荐算法的性能。在实际情况中，可以根据用户的隐式反馈推导出更丰富的偏序关系。例如用户对商品的购买次数和时间都可以表达对商品偏好的强弱。

如表1所示，相比i2，用户u1更喜欢i1，因为在购买时间相同的情况下，u1在i1上有更多的购买次数。用户u2可能更喜欢i1，因为在购买次数相同的情况下，u2在i1上的行为时间更近。对于用户u3而言更偏好i1，因为他在i2上没有任何隐式反馈。

表1 隐式反馈数据集

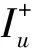
confid(fui,tui)=(1+αlog(1+fui/ε))e-β(t-tui)

(10)

式中：fui表示u对i的购买次数，tui表示u购买i的时间，t为当前时间，α为fui的影响因子，控制fui对整个置信度的影响，ε为缩放因子压缩购买次数的范围[9]。这里采用常用的指数函数e-β(t-tui)作为置信度的衰减函数[10]，β为衰减因子控制置信度随时间的衰减强度。

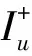
(11)

为了方便MBPR算法的描述，令Eu为集合E中与特定用户u相关的偏序集合，同样令Du为集合D中与特定用户u相关的偏序集合。

2.2 优化准则

对于一个用户u，可以同时使用Du和Eu中的偏序对训练模型参数Θ。设U为所有用户的集合，在BPR算法优化函数的基础建立如下的优化函数：

(12)

(13)

式中：bi表示商品i的偏离度。因此，模型参数Θ可以表示为参数集合{wu,hi,hj,bi,bj}。确定了模型参数Θ后，正则项R(Θ)可以表示为如下形式，其中λ为正则项系数：

(14)

2.3 模型训练算法

采用随机梯度下降SGD(Stochastic gradient descent)算法优化式(12)的目标函数。首先求得优化函数在每个参数{wu,hi,hj,bi,bj}处的梯度，然后沿着梯度相反的方向更新相应的参数。具体的更新公式如下：

(15)

(16)

(17)

(18)

(19)

其中,γ表示每次模型参数迭代的步长。训练模型参数Θ时，首先随机选取一个用户u∈U，然后判断与u相关的Eu集合是否为空，如果不为空，则从中随机取出偏序对(u,i,j)更新模型参数Θ，接着从与u相关的Du集合中随机取出偏序对(u,i,j)更新模型参数Θ，直到模型参数收敛，最后返回Θ。每次模型的迭代分别从Eu集合和Du集合中获取偏序对训练模型参数，Eu集合中的偏序对通过商品购买次数和购买时间建模用户的偏好属性，而Du集合中的偏序对通过已购买商品和未购买商品之间的对比为用户的偏好属性建模。同时利用Eu集合和Du集合中的偏序对训练模型参数，增强了用户偏好属性的准确性。模型参数训练算法的详细描述如下：

1: PROCEDURE Learn_MBPR(U,D,E,Θ)

2: initializeΘ

3: REPEAT

4: uniformly sample au∈U;

5: IFEu≠∅

6: draw(u,i,j) fromEu

7: updatewu,hi,hj,bi,bjaccording to Eq (15)～(19)

8: END IF

9: draw(u,i,j) fromDu

10:updatewu,hi,hj,bi,bjaccording to Eq (15)～(19)

11: UNTIL convergence

12: RETURNΘ

13: END PROCEDURE

3 实验与分析

3.1 实验数据集

隐式反馈在实际的推荐系统中是非常普遍的，但目前还没有这样的公开数据集，因此在本文的实验中，采用公开的数据集Netflix来模拟隐式反馈数据。Netflix数据集包含48万个匿名用户对1万7千多部电影的1兆多个电影评分。电影文件中的数据以四元组(电影ID，用户ID，评分，日期)的记录形式存在的，其中评分数值是1～5的整数区间，评分日期的时间跨度为1998年10月-2005年12月。由于Netflix数据集中的数据太多，评分数据多数集中在2005年，因此实验中从Netflix数据集中随机抽取2 000部评分较多的电影，以及1 000名用户在2005年的157 760个评分记录，记录的时间分布如图1所示。随机抽取50%的数据作为训练数据，剩下的50%作为测试数据。在训练数据集中又随机抽取50%的评分为3～5的数据将其转换为购买次数为1～3次的数据，其余数据不关心其具体的评分将其转换为二值数据。测试数据集也做同样的处理。

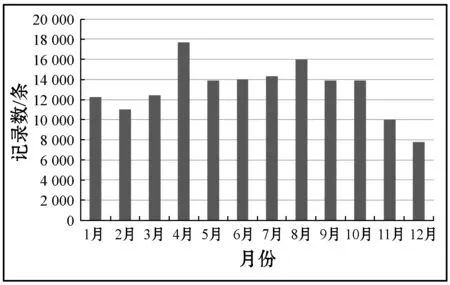
图1 评分记录的时间分布

3.2 评价指标

为了测试MBPR算法的性能，文中使用推荐算法中常用的性能指标Precision@N和AUC，其中Precision@N表示向用户推荐的N个商品中用户喜欢商品所占的比例，定义如下：

(20)

AUC的定义如下：

(21)

式中：E(u)的定义如下：

E(u):={(i,j)|(u,i)∈Stest∧(u,j)∉(Stest∪Strain)}

(22)

式中：Stest和Strain分别表示测试集和训练集。AUC越高代表了越准确的排序质量。一个随机正态分布的AUC是0.5，AUC的上限是1。

3.3 算法的性能分析

本节将通过实验对MBPR算法以及相关算法的性能进行测试。在实验中，矩阵分解模型中的隐因子数目k，模型参数Θ迭代的步长γ，正则项R(Θ)中的正则项系数λ经过多次实验取其最佳值，分别设置为：k=50,γ=0.01，λ=0.01，其他参数在具体实验中设定。实验指标Precision@N中的N取值为10。

3.3.1 购买次数与时间的影响

实验中单独测试购买次数和购买时间产生的偏序关系对推荐算法性能的影响。为了方便描述，分别称只考虑购买次数的算法为MBPR(N)，只考虑购买时间的算法为MBPR(T)。具体做法是：在MBPR(N)算法中将式(10)中的β设置为0，这样只考虑了购买次数对置信度的影响，同时α设置为10，ε设置为0.01；同理，在MBPR(T)算法中，将α设置为0，只考虑购买时间对置信度的影响，同时β设置为0.02。α、β以及ε的取值均为多次实验的最佳值。实验结果如图2和图3所示。

图2 购买次数与时间对Precision@N的影响

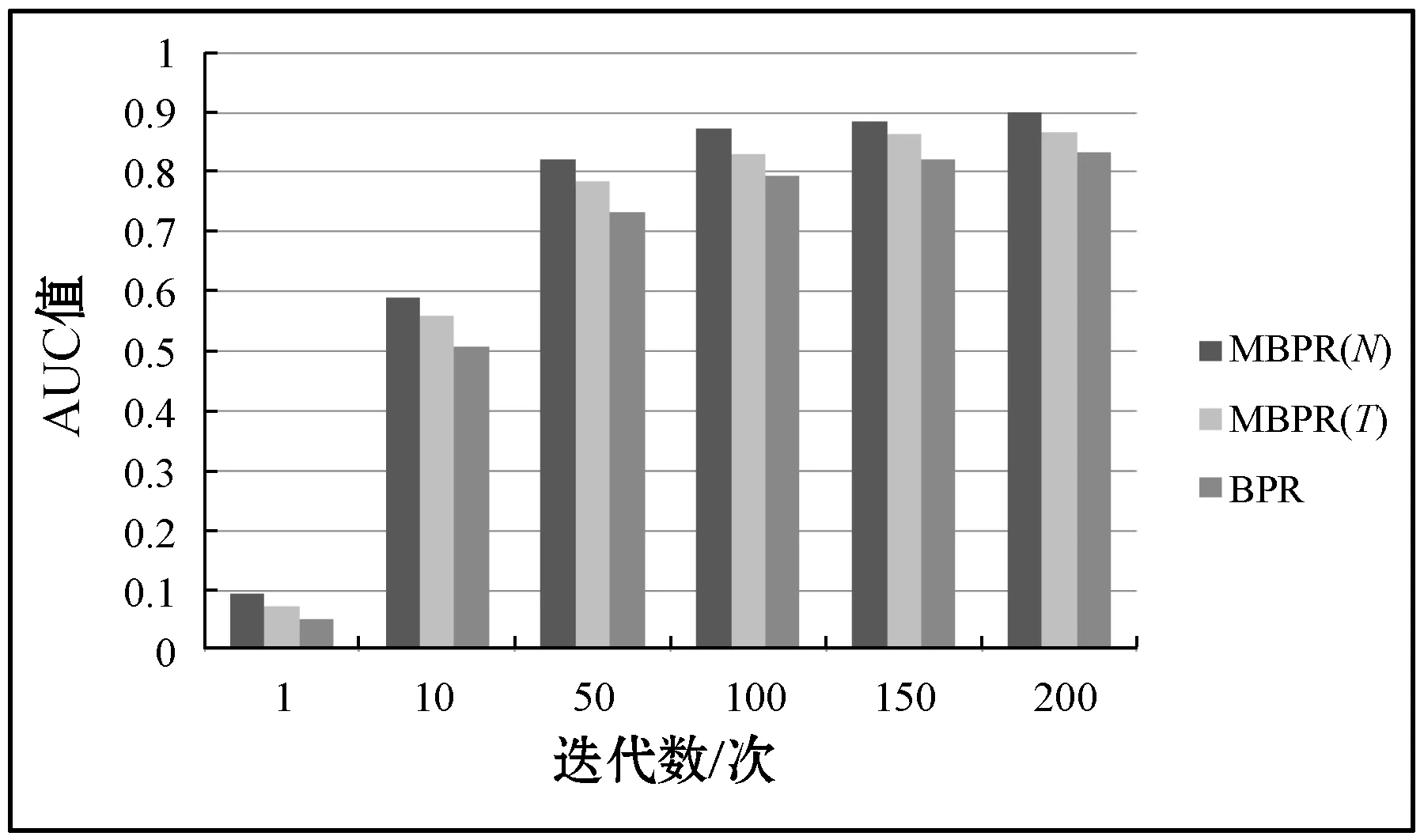
图3 购买次数与时间对AUC的影响

从实验结果看，MBPR(N)算法的性能最优，而MBPR(T)性能优于BPR。证明将购买次数与时间融入BPR算法中可以提高算法的性能，并且购买次数更能反映出用户对商品偏好的强弱。实验结果中，MBPR(N)算法相比BPR算法在Precision@N指标和AUC指标上分别提升了0.100 8和0.066 5。

3.3.2MBPR、BPR以及MF算法的比较

实验中将购买次数和时间同时融入到置信度的计算，产生偏序对训练模型参数，α设置为10，β设置为0.02，ε设置为0.01。对MBPR、BPR以及MF算法的性能进行比较，实验结果如图4和图5所示。

图4 三种算法在Precision@N上的对比

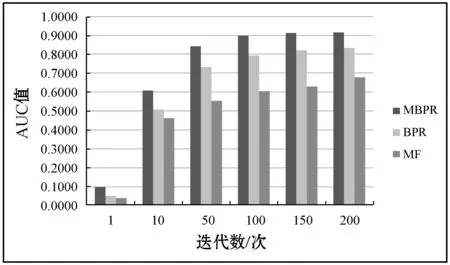
图5 三种算法在AUC上的对比

从实验结果看，MBPR算法在Precision@N和AUC性能指标上都有显著的提升。相比较BPR算法，Precision@N指标上提升了0.121 7，在AUC指标上提升了0.081 6。此外，随着迭代次数的增加，MBPR算法有着更好的收敛性。另一方面，从图5可以看出，MBPR算法和BPR算法与MF算法相比，在AUC指标上的差异比较明显，说明基于排序的推荐算法能产生更好的排序质量。

4 结 语

本文主要研究了隐式反馈数据上的商品推荐问题。首先分析了隐式反馈的特点，介绍了目前主流的推荐算法。接着，在BPR算法的基础上进行扩展，将隐式反馈中的购买次数和购买时间融入到偏序对的构建，使用更细粒度的偏序关系训练目标模型参数。最后，通过仿真实验，对本文提出的算法与相关算法的性能进行了比较和分析。实验结果表明，本文提出的算法在Precision@N以及AUC两个性能指标上都有明显的提升。在实际的推荐系统中，与显式反馈相比，隐式反馈数量更加庞大，内容更加丰富，形式更加多样化。如何更好使用隐式反馈的特性，进一步提升推荐算法的性能，是下一步工作的重点。