移动机器人在复杂环境中的在线路径规划
2018-10-23高佳佳陈超波
曹 凯,高佳佳,高 嵩,陈超波
(西安工业大学 电子信息工程学院,西安 710021)
目前,许多移动机器人平台变得越来越流行,它们的应用已经从静态实验室场景转移到人与机器人之间复杂交互的高度动态环境中,使得找到合适的路径变得更加困难,同时可能需要处理周围可移动的物体,因此移动机器人的路径规划显得尤为重要。路径规划是在静态和动态环境、模型约束以及不确定性的情况下,自动生成到达预定目标点的可行和最佳路径的过程[1]。
目前,尚未有一种“通用算法”可以解决任何条件、任何配置环境下出现的问题,例如:路径的最优性,机器人的运动学和动力学约束,有限的或无效的环境信息,计算负荷和效率等。在此,着重分析路径规划问题不同的解决方法,分别研究了A*,人工势场(APF),BRRT和PRM等4种路径规划算法的工作原理、存在的局限性以及相应的改进算法,然后利用设计的模拟器,在不同的场景下对4种方法分别进行在线仿真试验。通过分析试验结果,针对每种方法的性能表现给出了适用的场景和改进方法。
1 路径规划算法的分类与概述
1.1 路径规划算法分类
目前,路径规划存在很多不同的算法,可以大致分为基于图形、基于智能仿生和基于采样等规划算法。
基于图形的规划算法是将状态空间定义为占据网格,障碍物定义为不可访问的网格点。如果网格分辨率足够,搜索可用的网格点就可以保证产生解决方案,如可视图法、人工势场、A*以及D*等[2-6],较多用于城市环境探索、多智能体协作探索。然而,此类方法依旧存在着局限性,例如:人工势场容易陷入局部最小;A*和D*算法在网格分辨率较小时,搜索效率低,计算时间长的问题尤其明显。
基于智能仿生的规划算法通过研究自然界的一些社会行为,并且根据它们的原理归纳总结运动规律,最终模仿结构、行为,达到求解问题的目的。如蚁群算法、遗传算法、粒子群算法、神经络等[7-10],目前大多用于机器人协调控制、电力系统优化、网络路由优化问题。但是,此类方法本身的算法结构比较复杂,应用于复杂动态环境时会导致计算量激增,因而影响收敛速度,无法快速给出解决方案。
基于采样规划SBP算法具有简单通用、高效和概率完备的特点,是目前最受欢迎和最具影响力的路径规划算法[11-12]。它可以在没有明确的障碍物信息情况下,选择非结构有限数量的点相互建立连接并构建出可行轨迹的路线图,如概率路线图(PRM),快速随机探索树(RRT)以及变种算法RRT*,双向RRT(BRRT)等[13-16]。此类算法常应用于飞机机身清洁维护,高维空间环境探索,无人车辆的三维航迹规划以及具有非完整性运动约束的环境。
1.2 算法概述
(1)A* 算法
A*算法由斯坦福研究所的 Peter Hart,Nils Nilsson和Bertram Raphael于1986年提出,它在Dijkstra算法的基础上加入了启发式信息,解决了盲目遍历搜索的问题,并找到了解决从原点到目标的最小成本解决方案。启发式信息使启发搜索过程朝着可能“最快的”方向扩展,直至达到目标点。
A*算法流程可以概括为:
1)指定机器人的允许动作。
2)定义成本函数
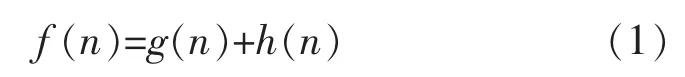
式中:g(n)为移动成本,即对应于将当前位置放入到某个邻居位置的成本;h(n)为启发式成本,即对应于从实际位置移动到目标位置的成本。
3)评估总成本f(n),并移至最低值的单元格。
4)重复1~3步骤,直到达到目标位置。
5)达到目标时,以最低成本计算最终路径。
A*算法的优点:如果解决方案存在,A*将根据其成本函数找到最优解;该算法在概念上简单且易于实现,且计算效率高。A*算法的缺点是,A*必须存储整个地图,内存要求较大,依赖于网格分辨率的大小,故在大型场景或高维操作空间中可能会出现问题。
文献[17]将分层策略应用到A*算法中并对其进行改进;文献[18]通过改进A*算法中的数据结构来提高效率。同时,也可将这些改进的策略结合起来以相互弥补不足,如双向搜索与方向诱导相结合、双向搜索与分层搜索相结合等。
(2)人工势场 APF
人工势场APF在1986年由Oussama Khatib提出,被广泛应用于机器人避障和路径规划。APF将环境(地图)建模为吸引或排斥机器人的场地,所有障碍物以与距离成反比的幅度排斥机器人,相反,它吸引了目标位置。势场总和可以定义为
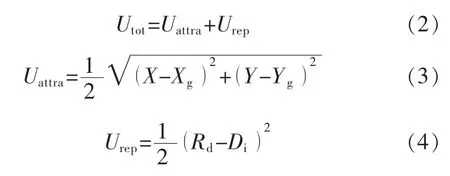
式中:Utot为总的势场;Uattra为引力场;Urep为斥力场;X,Y,Xg,Yg分别为机器人的当前位置和目标位置;Di为物体对机器人的影响距离;Rd为到最近的障碍物的距离。
虽然APF方法快速有效,但也有以下缺点和局限性:①容易陷入局部最小;②紧密间隔的障碍物之间不能形成路径;③在狭窄通道的情况下容易发生振荡。
APF的局部最小问题已被广泛研究,并有一些避免的方法,例如增加一个虚拟障碍来逃离局部最小值,使用模拟退火或自适应地调整障碍物势场函数以改进排斥场模型,使得机器人从局部最小值中逃脱。
(3)快速探索随机树RRT
快速探索随机树RRT算法由Steven Lavalle于1998年开发,它通过随机探索自由空间,构建一棵从初始状态开始寻找朝向目标状态的可行路径的树。
RRT算法的探索流程如下:①在搜索空间中选取一个随机样本;②找到该样本的最近邻节点;③从邻近节点中选择一个朝向随机样本的节点进行扩展;④根据邻近节点扩展的结果创建一个新节点;⑤将新的节点添加到现有树中并将其连接到其邻近节点;⑥当节点到达目标位置时停止循环。
RRT算法在过去的20年间陆续出现了许许多多的 变 种 , 例如 RRT*,RRT*-Smart,Bidirectional-RRT等。RRT*通过考虑最小长度成本以显著降低路径成本,表现出渐近最优性;RRT*-Smart旨在提高RRT*的收敛速度,产生最佳或接近最佳的路径,从而缩短执行时间;RRT-connect和Bidirectional-RRT分别从起始位置和目标位置创建两棵树,当两棵树相遇时找到解决方案;Expand-RRT使用新的随机采样点和无效路径中的节点概率性地重新规划路径。
RRT算法在低维、高维空间中均可进行规划,均匀采样可以有效地避免陷入局部最小,并且无需考虑运动目标的完整性和运动约束条件。但是随机采样也导致生成的路径并不是最优,从而导致路径成本、时间成本可能高于其他方法。
(4)概率路线图PRM
1996 年,Kavraki和Svestka开发了概率路线图PRM算法,该算法在配置空间中随机抽取样本并相互连接,然后使用基于图搜索的算法来确定起始点和目标点之间路径。
PRM算法主要分为2个阶段:
1)采样阶段(构建离线路线图)在工作区中绘制图形,方法是随机选择不在障碍物内部的点,并使用直线连接所有顶点对,检查所有顶点和边缘是否无碰撞。
2)学习阶段(在线规划)由于图形已经明确,因此可以使用基于图搜索的算法进行路径规划,定义连接点之间的欧式距离作为本地成本,欧几里德距离目标作为启发式成本,然后从起始点到目标点搜索出一条最优路径。
PRM方法是概率完备的,这意味着当时间趋于无穷时,它一定会找到解决方案。该算法在没有障碍物明确信息的情况下,也可以构建出可行轨迹的路线图。但是,当采样点太少或分布不合理时,可能无法找到最优解。计算具有复杂几何图形的精确解或大型场景规划时,所需时间可能呈指数倍增。
2 试验仿真与结果分析
为了分析前述4种算法,使用MatLab 2016开发了一种在线模拟器工具,它允许更改某些设置,如地图场景、算法类型和模拟类型。
该模拟器的GUI界面如图1所示。使用模拟器对不同的场景分别进行4种算法的测试,以便阐明并解释算法的主要特点。
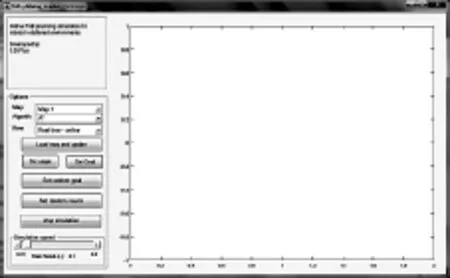
图1 模拟器的GUI界面Fig.1 GUI interface of simulator
2.1 场景1
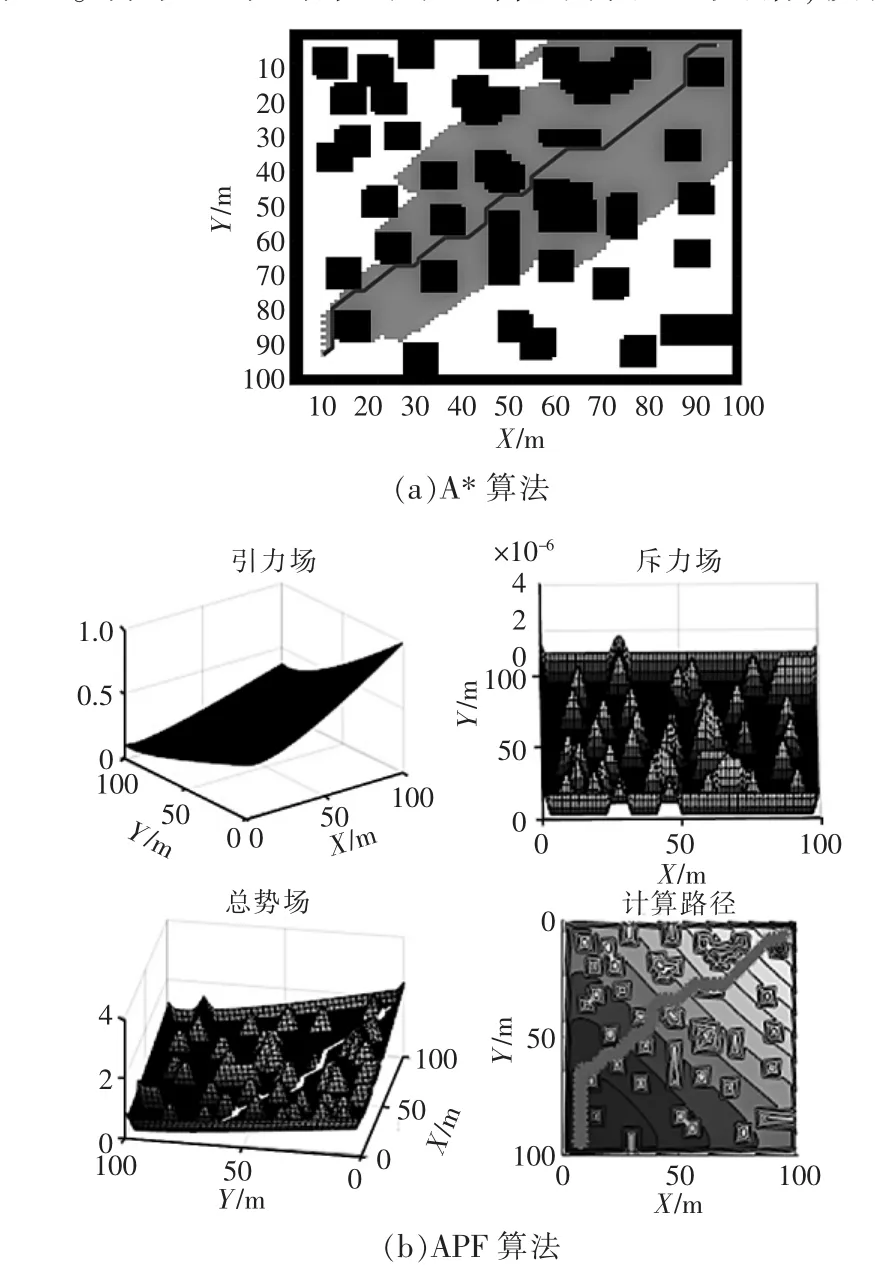
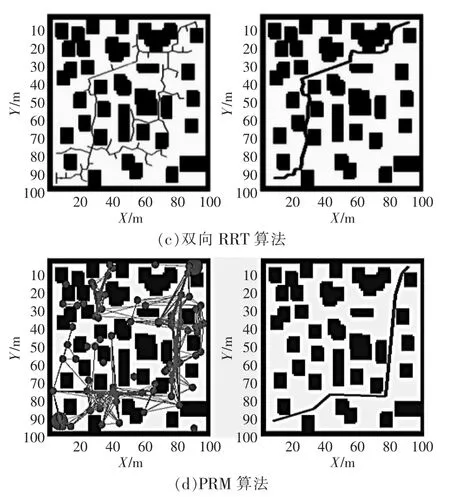
图2 场景1的模拟规划Fig.2 Simulation plan for scenario 1
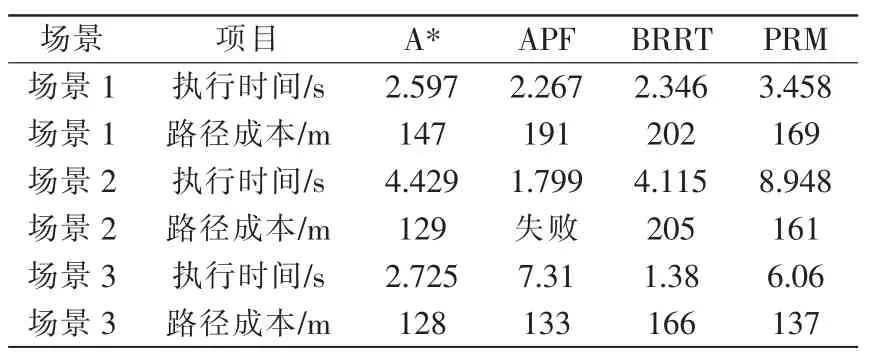
表1 仿真结果Tab.1 Simulation results
场景1的模拟规划如图2所示,其仿真结果见表1。场景1中密集的小型障碍物相互交错,模拟移动机器人在行进过程中的传感器动态交叉采集的情况。由图可见,4种方法均可找到可行路径,其中APF的计算时间最短,表明APF对于局部避障具有良好的性能。
2.2 场景2
场景2模拟了结构对称的凹形障碍物,该场景模拟规划如图3所示,仿真结果见表1。由图可见,A*算法给出了最佳路径,虽然执行时间相比于BRRT多0.276 s,但是路径成本远远小于BRRT。而APF在该结构化地图中,由于虚拟力的分布都是对称的,因此找不到可行路径。
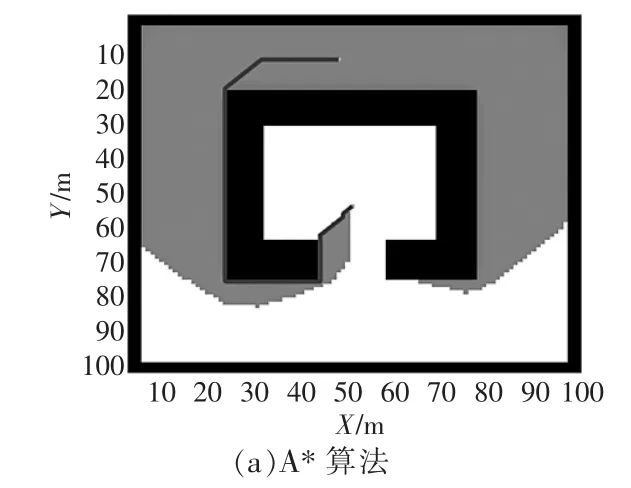
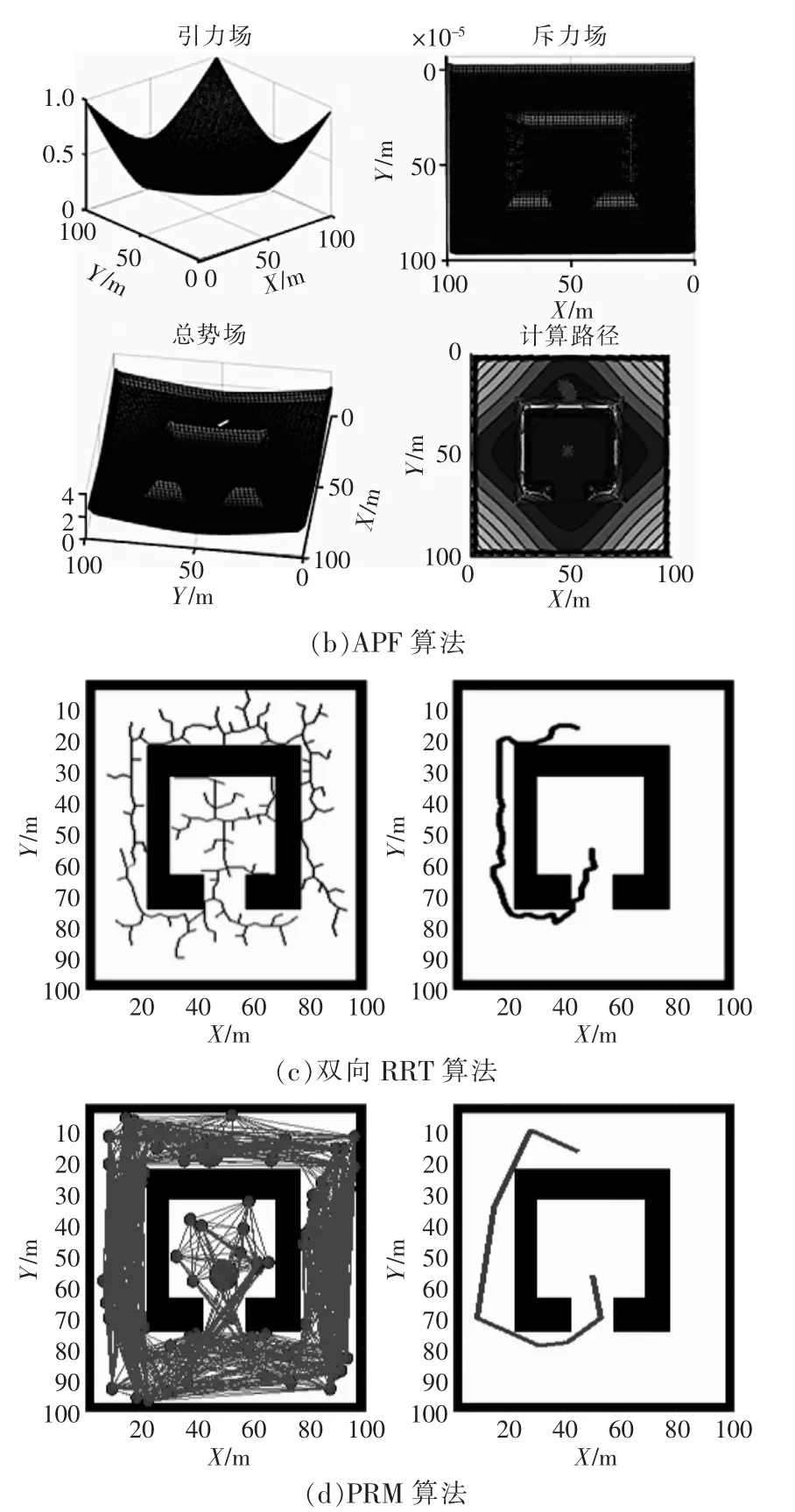
图3 场景2的模拟规划Fig.3 Simulation plan for scenario 2
2.3 场景3
场景3考虑了结构对称的室内走廊环境,该场景模拟规划如图4所示,仿真结果见表1。由图可见,最佳路径由A*和PRM给出,但这2种方法的计算时间相对较长:APF虽然跳出局部最优,并找到可行路径,但是执行时间较长;BRRT的执行时间最少,但路径不平滑导致路径成本较大。如果对BRRT算法的路径进行优化,可大大降低路径成本。
在考虑算法、地图和机器人位置之间的不同场景和组合之后,可以得出以下结论:
1)A*算法的收敛速度较慢,但可以保证最佳路径。可以通过降低地图分辨率来加速计算时间,但是如果分辨率太小,则A*无法保证最终路径的可行性和最佳性。
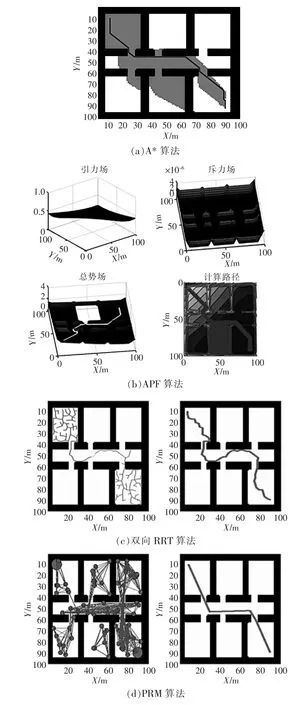
图4 场景3的模拟规划Fig.4 Simulation plan for scenario 3
2)APF算法通常计算时间较短,但是在充满狭窄通道的场景下,或当某个点的引力和斥力大小相等、方向相反时,APF方法往往容易陷入局部最优或出现震荡。因此,在控制环中加入一种局部避障算法,可以有效地解决APF存在的问题。
3)同为概率采样方法,PRM生成的路径比BRRT的路径更平滑和更短,一方面是BRRT节点扩展预定义的最大步长和盲目探索,都会影响路径优化。另一方面,PRM在整个空间中随机采样,并基于它的随机点可以找到最短距离。当然,由于这2种算法都存在随机性,因此也会存在BRRT比PRM更优的情形。
3 路径规划算法的发展趋势
在路径规划的研究中,每个规划算法都有适用的场景,但是也存在一些不足之处,因此路径规划的研究重点依然是研究新的、高效的改进路径规划算法。此外混合路径规划也将成为未来路径规划研究发展的方向。具体表现在以下几方面:
(1)传统算法与随机算法相结合。
a.利用A*的启发式特性引导RRT进行目标偏向采样,以减少执行时间、扩展节点数量以及路径成本;b.RRT的随机性可以帮助APF跳出局部最优解,并快速找到成本较低的路径。
(2)遗传算法与神经网络相结合。
利用神经网络控制机器人的运动规则和神经元感知器获取未知环境的信息,再利用遗传算法实现神经网络的权值设置,实现未知环境下的机器人路径规划。
(3)蚁群算法与人工神经网络相结合。
将蚁群算法与人工神经网络相结合,可以减少空间复杂度,同时提高路径规划准确率。
(4)多机器人合作的路径规划。
多机器人合作进行路径规划已经成为新的研究热点之一,如何划分未知环境,如何对机器人进行分功,如何设置机器人的体系结构及机器人间的通信方式等成为新的研究问题,这些问题的解决能够更好地减少机器人间的冲突问题,以便进行更好的路径规划。
4 结语
路径规划算法通常都有很多变种,因为它们一般不能同时满足所有要求,这也就意味着没有任何一种算法可以适用于任何场景,且快速、低成本的规划出最优路径。全局路径规划和局部路径规划结合使用就可以保证一个相对快速而且最优的路径,并且在复杂的动态场景、高维环境以及非完整和运动约束环境中均是有效的。路径算法混合使用不仅可以利用彼此的优势,还可以弥补自身所存在的缺点,以此提高路径规划的效率和鲁棒性。期望本文对于从事相关问题研究的相关人员和未来的发展具有一定的参考价值。
