基于小波变换的QRS波特征提取算法研究与实现

王 莉，郭晓东 ，惠延波，何宇宸

（1.河南工业大学 电气工程学院，郑州 450001.2.Wakefield School，Virginia USA）

心电信号包含大量体现心脏节律的信息，客观反应了心脏的生理特征，是诊断心脏疾病的主要依据。心电图ECG用于临床心脏病诊断，主要依赖医师丰富的临床经验。然而，心电图种类多、变化大，医师在长时间诊断中可能存在漏检、错检的情况[1]。因此，从心电图提取特征信息，实现自动检测成为研究热点。

一个典型的心电信号由P波、QRS波、T波构成，心电信号特征点任一幅值和时间跨度均可被视作一种特征。近年来，研究心电信号特征提取的算法不断涌现。文献[2]提出一种基于Pan-Tompkins方法和小波变换的组合算法；文献[3]提出一种基于卷积神经网络的QRS检测方法；文献[4]提出一种基于二次滤波器的QRS检测算法；文献[5]通过计算并比较R波左侧或右侧相邻两点的斜率变化来判断Q波和S波；文献[6]采用基于自适应双阈值ADT与回溯重检机制的检测算法检测QRS波。文中在对心电信号去除干扰的基础上，采取一系列策略实现QRS波的准确定位，并基于灵敏度和正检测率准则对算法的有效性进行评估。

1 小波变换处理心电信号原理

1.1 小波变换去噪原理

小波变换去噪可以通过小波变换快速算法实现，即Mallat算法。已知小波函数ψ（t）和尺度函数φ（t），Mallat算法分解公式为

式中：h｛k｝为 φ（t）对应的低通滤波器；g｛k｝为 ψ（t）对应的高通滤波器；ci，k，di，k分别为第 i层的低通系数、高通分解系数。

利用卷积的可交换性，重构公式为

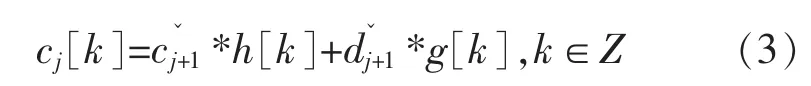
1.2 小波变换检测信号突变点原理

设 f（t），ψ（t）∈L2（R），记

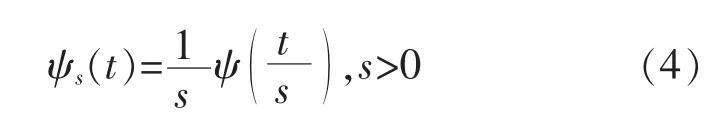
则称

为 f（t）的小波变换。

根据小波变换的定义和卷积的性质，有

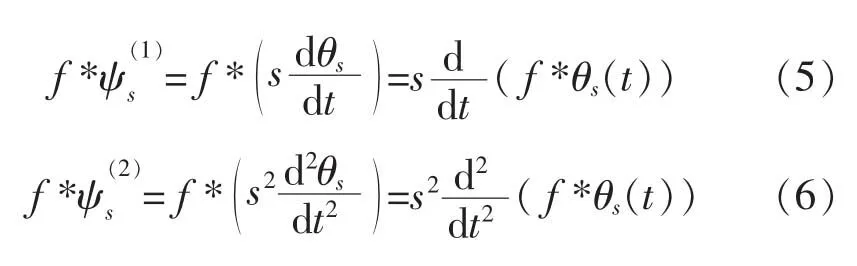
结合Lipschitz指数可知，当选取光滑函数θ（t）以后，信号 f（t）的突变点可以通过检测小波变换f的模极大值得到。

2 心电信号去噪

心电是微弱的生物电信号，在测量过程中极易受到外界的干扰，常见干扰有基线不稳、肌电干扰和工频干扰[7]。

对心电信号进行分析前必须对心电信号去噪处理，传统的去噪方法中常使用高通滤波器或低通滤波器，但是滤波器设计复杂，同时会使心电信号丢失重要的信息，不利于后续研究。自适应滤波器也被用于心电信号去噪，但是该方法去噪效果并不理想[8]。小波变换在时频域上对心电信号进行分析，最大程度地保留了心电信号的重要信息，故在此提出一种采用小波变换有选择地抑制各层细节系数对心电信号去噪。

2.1 去除基线漂移干扰

心电信号频率通常分布在0.05～100 Hz，基线漂移频率不大于0.3 Hz[9]。MIT-BIH Arrhythmia Database数据样本噪声来源主要是基线漂移，采用小波变换去除基线漂移干扰，主要有以下3个步骤：

步骤1确定小波分解层次，并进行分解计算。

MIT-BIH Arrhythmia Database中的心电数据样本采样频率为360 Hz，根据采样定理，心电信号的最高频率为180 Hz，对心电信号进行8层分解，可以得到心电信号分解的近似系数a8和一组细节系数d1—d8，其中d8的频率范围为0～0.703125 Hz。由基线漂移噪声的特点和小波分解系数频率分布范围，选取小波分解尺度为8[10]。选取db5小波，对心电信号8层分解的小波细节系数如图1所示。

步骤2小波分解高频系数阈值量化。

基线漂移的频率主要分布在小波细节系数d8中，考虑到心电信号中也包含有大量的高频信息，可以在小波域上将d8细节系数所在下标小于40%的细节系数成分舍弃，将d8细节系数所在下标大于40%的细节系数作为新的小波细节系数d8。

步骤3小波重构。

将小波近似系数a8和新的小波细节系数d8及d1—d7进行逐级重构。

原始心电信号和重构的心电信号如图2所示，由图可见，该方法保留了相对完整的信息，且波形比较平滑，对心电信号基线漂移去噪效果较好。

图1 小波分解细节系数Fig.1 Wavelet decomposition detail coefficient

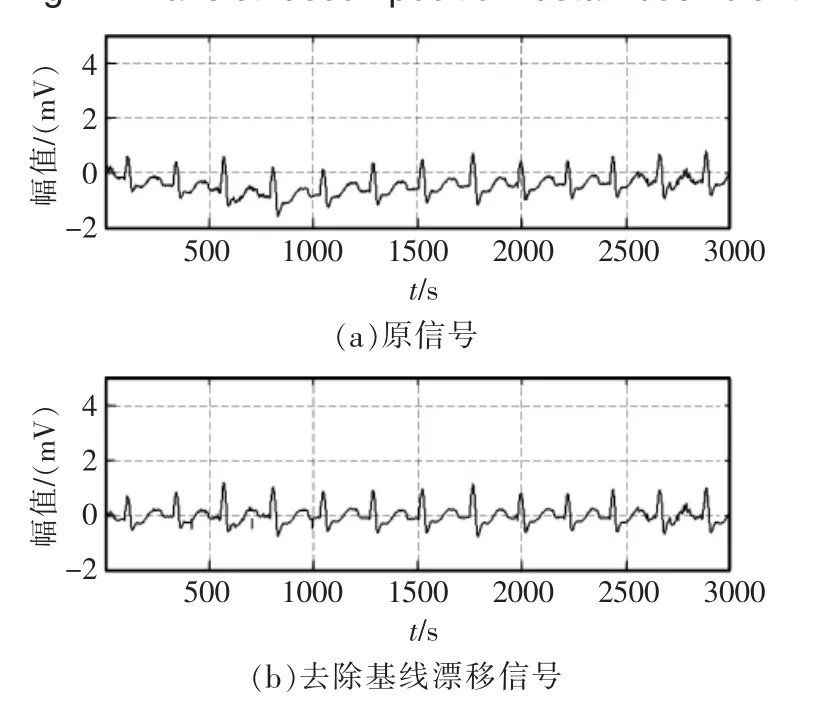
图2 原信号和去除基线漂移信号Fig.2 Original signal and removing baseline drift signal

2.2 不同小波函数消噪结果对比

选用峰值信噪比PSNR和均方根误差MSE评价不同小波函数去噪效果。PSNR数值越大，MSE数值越小，则去噪后信号和原信号近似程度越好。PSNR和MSE的定义为

式中： f（i， j）和 g（i， j）为原始信号、去噪后信号图像；M，N分别为它们的长、宽。

选取 db4，db5，db6，sym4 常用小波对心电信号去除基线漂移，去噪结果见表1。由表可知，db5小波在去除基线漂移中PSNR最大，达到14.0583；MSE最小，达到0.0393。试验结果表明db5小波去除基线漂移效果最好。

表1 常用小波消噪结果Tab.1 Commonly used wavelet denoising results

3 QRS特征点定位算法

在一个心电信号周期中，QRS波是心电信号中最突出、最重要的部分，它不仅是诊断心脏疾病的重要依据，也是定位分析其它波形的基础。本研究经过大量的试验对比，选取对db函数改进的sym4为基小波，在第4尺度上对心电信号进行特征提取。

3.1 R波峰值定位

依据小波变换检测信号特征点原理，采用sym4小波函数，对心电信号4层分解，原始心电信号和各尺度心电信号如图3所示。可以看出R波峰值点和小波域上的极大极小值过零点相对应。

图3 心电信号和4层分解小波系数Fig.3 ECG signal and 4-layer decomposition wavelet coefficients

R波峰值定位算法步骤如下：

步骤1将去除基线漂移的心电信号X（n）作4层小波分解，得到小波变换系数矩阵wsig。

步骤2在小波变换域上，寻找前3 s内的极大值点Max和极小值点Min，然后分别求取前10个极大值点和后10个极小值点的平均值，以极大值和极小值平均值差的0.45作为阈值寻找整个信号中的极大值点和极小值点，得到极大极小值对。

步骤3求取极大极小值对的过零点，并记录该点对应的值R（i），初步认为R（i）是R波峰值点。

步骤4对R波峰值点校正，取R（i）前后各5个采样点，求取10个采样点中的最大值，将该点作为R波峰值点。

步骤5排除误检，计算R波间期平均值RRmean，判断相邻R波时间间隔是否小于0.4RRmean。如果是，则去除R波幅值比较小的点。

步骤6排除漏检，判断相邻R波时间间隔是否大于1.6RRmean。如果是，则阈值减小为原来的1/2，在该时间段内重新寻找正负极大值对，判断是否存在过零点。

3.2 Q波、S波峰值定位

通过观察分析QRS波群持续时间内，R波峰值和QS波峰值之间的几何关系，本研究采用平面几何的方法定位Q波和S波峰值，具体算法如下：

①对信号进行连续小波变换，如果R波正向，在R波前20 ms内寻找第1个极小值点。反之，寻找到第1个极大值点，并把心电信号上对应点记为n。

②在n点前极小的一段距离取一点，记为m。连接点m和R峰值点r，得到直线mr。

③从点m开始到r，依次计算各点到直线mr的距离d，则d最大的点即为Q波峰的位置。

从R波向后30 ms的时间内定位S波峰值，具体过程与Q波峰值定位相似。

3.3 QRS波起止点定位

QRS波的起点就是Q波的起点，终点就是S波的终点。经过试验分析，QRS波的起点和终点分别与其波形两侧的过零点近乎处于同一位置。定位到QS波峰值点后，分别向前向后搜索最靠近基线的点，即可认为是QRS波的起点和终点。

3.4 QRS波特征点定位算法实现

对原始信号截取2000个采样点，在小波变换域上实现QRS波峰值点和起止点定位，QRS波特征点定位结果如图4所示。由图可见该算法实现了对QRS波的准确定位。

4 算法验证

随机选取MIT-BIH Arrhythmia Database中16组样本对QRS波检测算法验证，采用灵敏度Se和正检测率P+两种准则评价算法的准确性，即

式中：TP为QRS波的正确检出数；FP为QRS波的错误检出数；FN为QRS波的漏检数。

图4 心电信号QRS波特征点定位Fig.4 Location of ECG QRS wave feature points

16组心电数组QRS波特征提取结果见表2。由表可知，该算法对QRS波的检测取得了较好的结果，算法的检测灵敏度达到99.85%，正检测率达到99.86%。

表2 QRS波定位结果Tab.2 QRS wave positioning results

5 结语

通过小波分解重构快速算法去除心电信号基线漂移，算法简单且去噪效果较好；选用峰值信噪比和均方根误差评价4种常见小波函数在心电信号中的去噪效果，结果表明db5小波去噪效果最优；依据小波变换域上的极大极小值过零点检测R波峰值，并采用一系列策略排除了误检和漏检，实现了R波的准确定位；采用平面几何的方法定位QS波峰值；该算法对QRS波特征提取灵敏度达到99.85%，正检测率达到99.86%。结果表明，该算法对于心电信号的预处理和特征提取是有效的，对心电疾病的分类诊断具有重要参考意义。