一种高可靠分辨波束形成算法的应用研究

张蓓宋克

（杭州应用声学研究所 杭州 310023）

1 引言

现代声纳设备主要通过水声传感器阵列结合信号处理技术实现水下目标的检测、定位、跟踪、识别等［1］。实时准确地定位目标是后续信号处理的基础，这有赖于高可靠、高分辨的DOA（Direction of Arrival）估计技术，在水声信号处理中，DOA估计是通过波束形成技术实现的。

常规波束形成技术（Conventional Beam Forming）运算简单，稳健性好，但其旁瓣高，主瓣宽，方位分辨力受制于“瑞利限”［2～3］，性能提升依赖于增加物理孔径和增多阵元数量，存在多目标分辨和虚警率高的问题。20世纪60年代以后，提出了多种具备高分辨力和抗干扰能力的自适应波束形成算法（ABF，Adaptive Beamforming）［4～6］，在声纳装备中常用的有MVDR（Minimum Variance Distortionless Response）和 STMV［7］（Steered Minimum Variance）算法，然而ABF稳健性较差［8］，在实际应用中，环境参数失配和系统误差会导致算法性能大幅下降甚至崩溃。

本文使用一种新的波束形成算法——FB（Functional Beamforming），算法对数据协方差矩阵进行特征值分解指数重构，具有旁瓣低、主瓣窄的优点，可实现对目标的高可靠分辨。

2 算法模型

对于M阵元的水听器阵列，假设各阵元接收信号表示为xi(t),i=1,2,…,M。则有

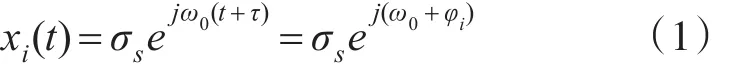
其中相位差φi由阵元位置与来波方向决定，σs表示接收信号强度。当信号带宽B远小于载波频率f0时，σs变化缓慢，考虑接收噪声n(t)，则阵元i接收信号可表示为

从而阵列接收矢量可表示为

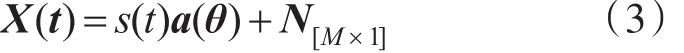
若有L个声源，则接收矢量为

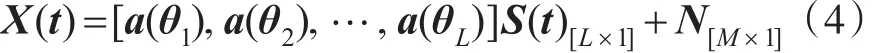
其中，S(t)=[s1(t),s2(t),...,sL(t)]T为输入信号矢量。

波束形成器输出为

其中，W 为M×1的权向量。

波束形成器总输出功率可表示为

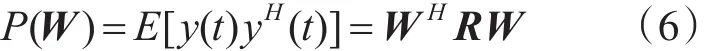
其中，R为数据协方差矩阵，R=E(X(t)XH(t))，对R 进行特征值分解［9］，即

其中，Λ表示由特征值构成的对角矩阵，Λ=diag(λ1,λ2,...,λM)，U 表示由特征值对应的特征向量组成的酉矩阵，U=[u1,u2,...,uM]，ui为M×1的归一化特征向量|ui|=1，且有UUH=UHU=E。协方差矩阵表示如下：

若仅有一个非零特征值λk，则有

对于常规波束形成器，输出功率PCBF(a)=aHRa=λkaHukuHka=λk|aHuk|2。其中 a表示束控方位的归一化驾驶矢量，则有PCBF(a)=λkcos2a,uk，式中 a,uk表示矢量a和uk的之间夹角，当a=uk时，空间谱达到峰值，即λk。

定义FB算法如下：

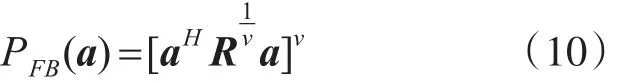
其中

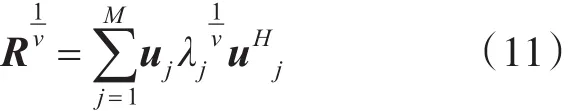
其中，ν为指数因子，由式（10）定义可推导，当仅有一个非零特征值（对应仅一个信号源）时：

当ν=1时，该算法退化为常规波束形成；当ν＞1时，峰值不变，旁瓣幅度指数下降；当ν=-1时，该算法即为MVDR算法的功率谱输出。

常用的波束形成算法中，常规波束形成算法分辨力较差，难以区分方位相近的多个目标，MVDR与STMV算法需要矩阵求逆运算，均存在鲁棒性差的缺点，当阵型、环境参数略微失配时，算法性能急剧下降［10］。FB算法取ν＞1时，能保证在波达方向能量最大的前提下，使旁瓣变低，主瓣变窄。算法稳健性随着ν增大而减弱，因此在实际使用中需根据模型找到最佳的指数因子ν。

3 仿真建模

依托于某型主动声纳样阵构建一个20阵元均匀线阵模型［11］。选取不同的指数因子ν，观察空间谱的方位估计情况。算法流程如图1所示。

1）仿真实验一

主动声纳信号处理中STMV算法较为常见，在信噪比较低（SNR=-15dB）的场景下，比较CBF、STMV与FB三种算法的结果。

仿真目标信号单频10kHz，分别从0°和60°方位入射。

图2中信号入射方位为0°，CBF、STMV与FB的主瓣宽度分别为25°，19.4°，12.8°；图4中信号入射方位为60°，CBF、STMV与FB的主瓣宽度分别为2.98°，2.87°，0.39°。由图2、3可见，FB算法具有旁瓣低且主瓣窄的优点，可以实现高可靠分辨。

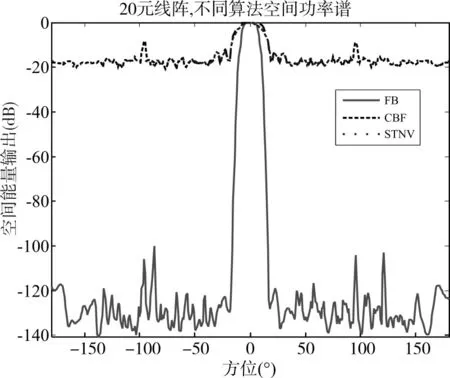
图2 CBF、STMV与FB结果对比（0°）

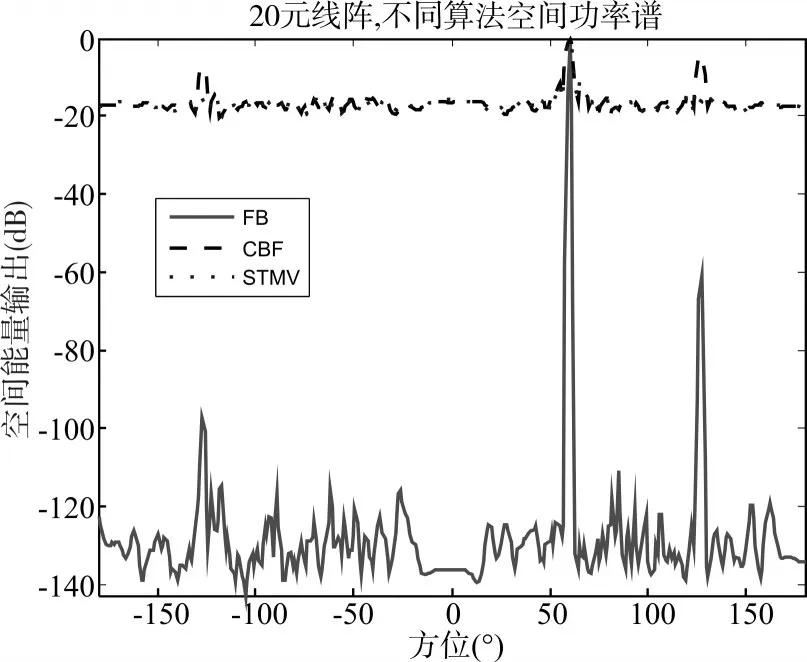
图3 CBF、STMV与FB结果对比（60°）

并且FB算法在计算过程中不涉及矩阵求逆运算，稳健性优于常见的自适应波束形成算法，如MVDR［12］、STMV等。

2）仿真实验二

仿真目标信号单频10kHz，从0°方位入射，分别设置ν=1 ,2 ,4 ,8 ,16 ,32 ,64 ,128，方位功率谱输出如图4所示。

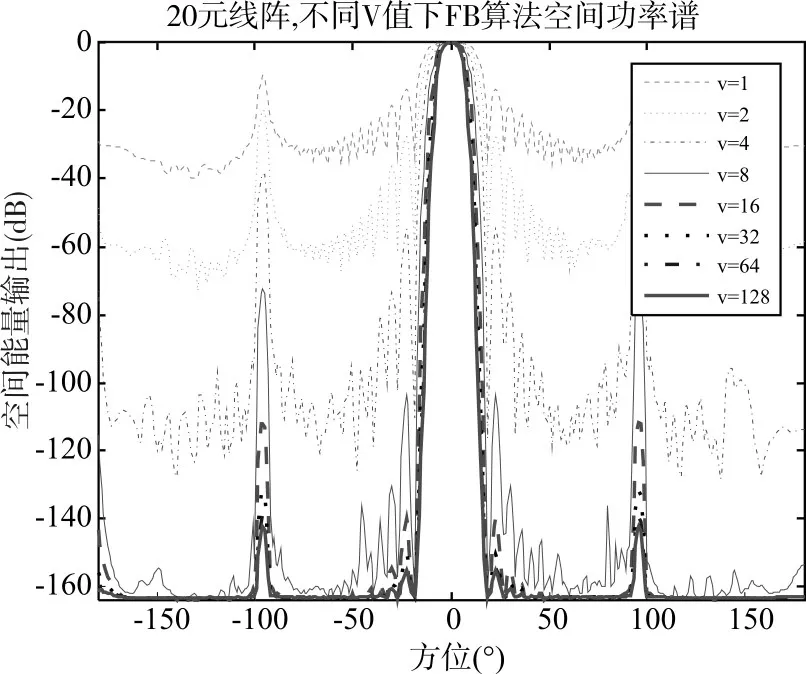
图4 FB算法不同ν值输出结果

由图4可以看出，当ν=1时，即为常规波束形成，此时旁瓣高且主瓣宽，可靠性弱、分辨能力低。随着ν值增大，旁瓣衰减增大，主瓣宽度变窄，从而可靠性与分辨力增强。当ν＞16时，旁瓣高度与主瓣宽度趋于一致，性能上提高不大，因此选取ν=16，不仅能较好地提高波束形成性能，且能降低FB算法的运算量，并保证算法稳健性。

4 试验数据验证

采用FB算法对该型主动声纳样阵某次湖试数据进行处理，对比CBF、STMV与FB算法。

目标信号单频10kHz，从0°方位入射，输出结果如图5所示。

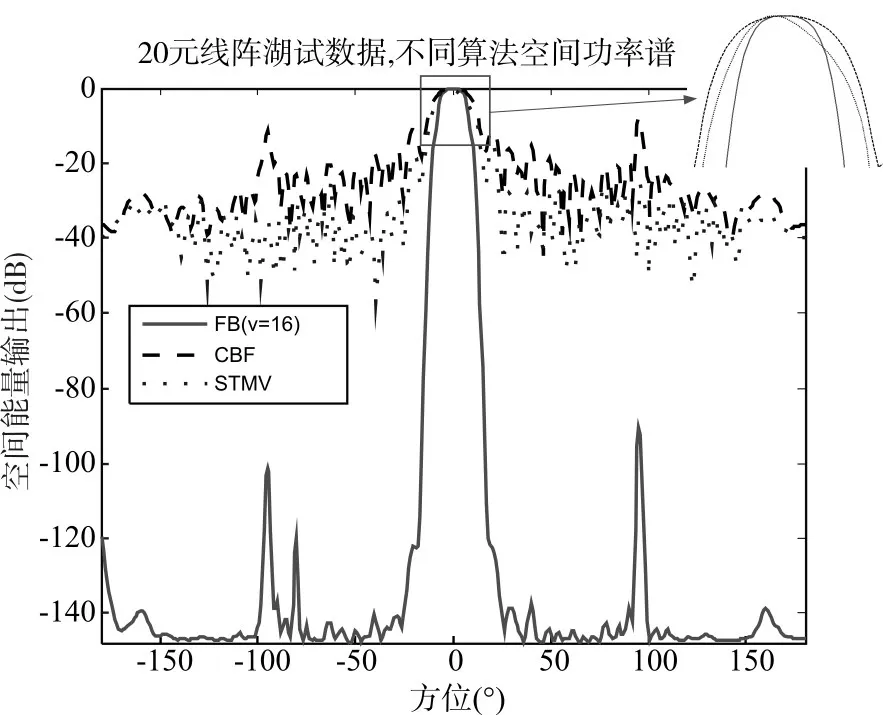
图5 CBF、STMV与FB试验数据处理结果（0°）

目标信号单频10kHz，从90°方位入射，输出结果如图6所示。

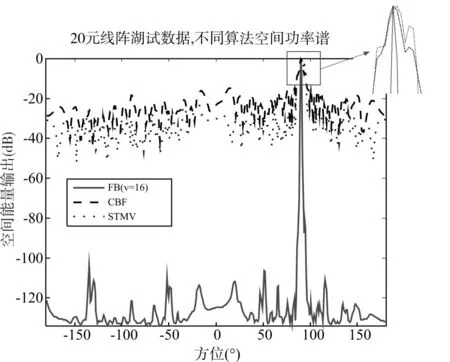
图6 CBF、STMV与FB试验数据处理结果（90°）

实际试验数据存在混响和水面水底反射等杂波，信干噪比较低。由图5、图6可见，对存在杂波干扰等的试验数据，自适应的STMV算法出现方位估计偏差；而常规的波束形成算法旁瓣高，主瓣宽；相比于CBF和STMV算法，在ν值选取最优的情况下，FB算法具有很好的旁瓣抑制能力，且主瓣窄，分辨力高，可实现高可靠的分辨能力。

5 结语

本文采用一种对数据协方差矩阵进行特征值分解指数重构的波束形成算法FB。

通过仿真实验和实际数据处理将本算法与CBF和STMV性能进行对比，证明了FB算法具有旁瓣低、主瓣窄的优点，并且在计算过程中不涉及矩阵求逆运算，稳健性优于MVDR和STMV，可实现对目标的高可靠分辨。

同时，仿真实验从波束形成性能和计算量两方面取折中，通过范围枚举的方式得到了最优ν值，从工程应用角度进一步优化了FB算法。面对不同阵列分布形式和对波束形成性能、计算量要求的差异，这种计算最优ν值的方法普遍适用。