基于平均备件保障概率的备件库存优化模型研究
2018-10-23付兴方吴佳康
袁 园 付兴方 吴佳康
(空军勤务学院航材四站系 徐州 221000)
1 引言
随着飞机使用时间的延长,即使飞机的可靠度再高,飞机各系统的部件也难免会发生故障,则就需要预先储备好相对应的备件用来更换。为了合理地进行库存管理,许多学者已经提出许多库存预测模型[1~4]。阮旻智[1]等以装备可用度为中心,建立(R,Q)库存策略下的备件协调订购模型;刑国平[2]等利用灰色关联支持向量机对备件库存消耗进行预测;现今无论是国内国外,都将备件保障概率作为确定备件数量的指标[5~6]。李源[5]就是利用备件概率保障作为指标,建立了备件需求模型,更加确定备件的需求量。林宝国[6]也利用航材保障概率,建立初始备件单个单元需求预测模型和多个单元需求预测模型,为初始备件精确保障提供理论依据。但是传统的备件保障概率有着极强的局限性,使模型应用范围受到限制。故在对备件保障概率进行分析的基础上,提出系统平均备件保障概率,结合边际效应分析对备件库存进行优化处理。
2 模型描述
2.1 实时送修策略下的备件生灭过程分析
实时送修是在实时补充库存策略基础上建立的,该库存策略的含义是当产生故障件后,立刻发出订购申请,申请数为1。在实时送修的策略下,当飞机产生故障,需要备件时,立即进行换件维修,故障件及时送修。若库存水平保持恒定,有如下函数:

式中:s为初始库存数量,S1为现有库存数量,S2为在修数量或再供应数,S3为备件短缺数量。
由上式可知,若库存水平保持恒定,备件需求的产生和送修过程就是一类维修保障的生灭过程。对于库存水平为s的情况,在整个保障过程中,一共有s+1种状态不会产生备件短缺的情况。总体来说只要s≥S1+S2,就不会出现备件短缺的情况。即需要备件时,能够得到保障。其概率就是备件保障概率。
2.2 平均备件保障概率
备件保障概率是指在规定的时间周期内,装备的备件需求能够被满足的概率。传统的保障概率一直忽略一个现象,就是在整个保障周期中,不同时间段对应的保障概率是不同的,其大小会随着时间增加不断地下降,如图1。而传统的保障概率所对应的却是期末时刻前的保障概率。而平均备件保障概率就是求整个时域内保障概率的平均数,使得所求概率更具代表性。

图1 保障概率与时间的关系
当备件的失效率等于常数,即其寿命为负指数分布时,传统的备件保障概率P0(m,λ,t0)可由下式表达:

其中,m为库房存数数量;λ为备件失效率;t0为补充供应周期内备件累计工作时间。
对式(1)进行积分,推导出平均备件保障概率,如下式:
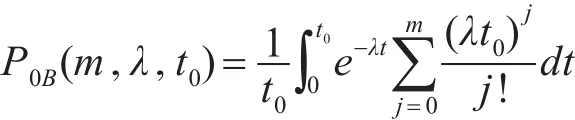
上式是单个备件的平均备件保障概率。但是若是从单个备件库存考虑,会缺乏备件之间的相互联系,所以从飞机系统出发,求飞机单个系统内部所有备件库存,使得计算结果更具有整体性。
2.3 系统平均备件保障概率
系统平均保障概率是指当系统内部某一个部件发生失效时,能否得到保障的概率。由于系统内部各个部件发生失效的概率是相容的,即系统在任务持续时间段内第i个部件发生故障时,并不排除其他部件同时发生故障。因而也不能将系统缺少备件的概率表达成各个部件缺少备件概率之和,即
式中:Fi(tS)为第i个部件在任务时间内发生故障的概率;为第i个部件在规定的备件补充周期内得不到备件保障的概率;mi为第i个部件在一个备件补充周期内配置的备件数。
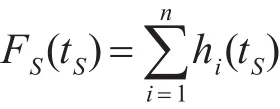
式中hi(tS)就是第i个部件的独立失效概率,即当任意一个部件失效时,系统停止工作。这样就可以得到系统备件得到保障的平均概率:

可以利用马尔科夫随机过程求取独立失效概率hi(tS)。
最终可求的独立失效概率hi(ts)
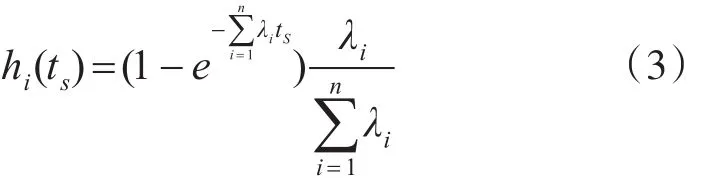
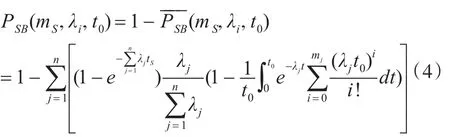
将式(3)带入式(2)中得:
2.4 库存优化模型
本文是以保障概率取最大为目标函数,以保障经费为约束条件。故库存的优化模型如下:

式中:ts为任务持续时间,cj为编号为 j的部件采购单价,C为总的保障费用。
对目标函数进行分析,可以看出保障概率函数是一个单调递增的函数。证明如下:假设系统中某部件库存数量为m,其保障概率为P()m ,则:
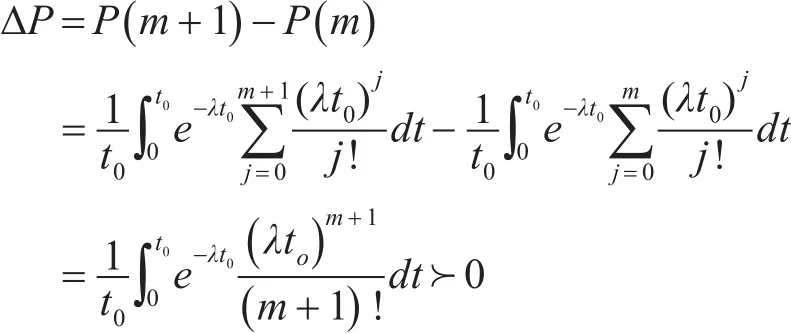
表1给出三个备件的失效率,其工作时间一样,t=500h。图2为平均备件保障概率与库存量之间的关系。

表1 不同备件的失效率
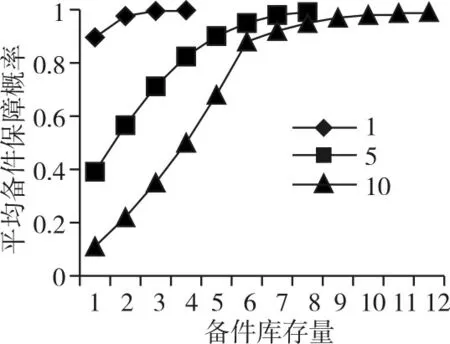
图2 平均备件保障概率与库存量之间的关系
从上面叙述可知,平均备件保障概率函数为单调递增的函数,其数值的大小与备件本身的失效率有关,也与其工作时间的长短有关。所以需要知道备件本身的失效率和系统工作时间。失效率可以从历史数据中平均故障间隔时间推出,系统工作时间可以从年度任务中得知。对于在利用边际效应分析时,具体详细步骤如下:
1)将备件的库存量si记为0,作为备件初始库存量。
2)进行迭代时,确定需要调整的控制量,即需找最大的边际效益maxΔpici。
3)将所对的备件编号所对应的库存量进行加1,其余产品备件数量恢复原始量。
4)根据所确定的库存量,确定对应的保障经费,若是符合目标值,迭代完成,若是不符,重新进行步骤2),3)。
其流程图如图3。
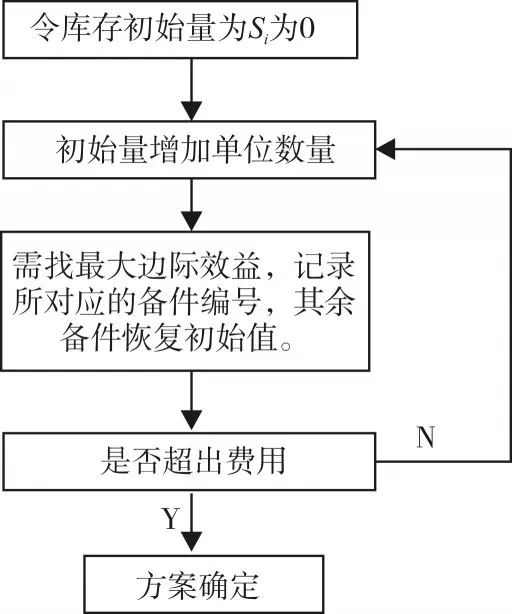
图3 边际效应分析流程图
3 算例应用
某型飞机某系统是由LRU1、LRU2和LRU3组成,它们重要性一致。其中周转时间为250天,系统每天工作时间为4h,保障经费为50万元,在实时补充的库存策略下,考虑备件费用,结合边际效应分析法,以平均备件保障概率为约束条件,给出备件供应策略,并对结果进行分析。LRU1、LRU21和LRU3的参数如表2。
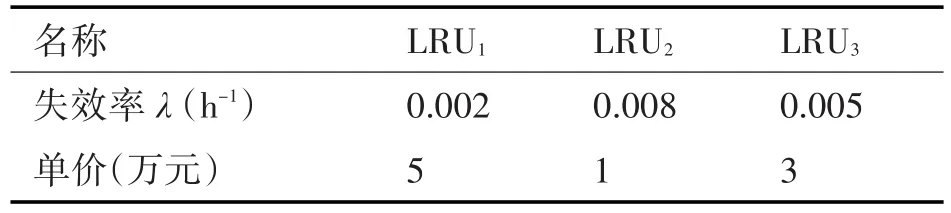
表 2 LRU1、LRU2和 LRU3参数
根据所给的参数,Si=0。LRU1、LRU2和LRU3平均备件保障概率变化如表3、表4和表5。

表3 LRU1平均备件保障概率变化数据表
该模型最终确定的库存方案:4个LRU1、9个LRU2和7个LRU5,最终系统平均保障概率为0.95,其过程如图4。
结果表明,该库存优化模型以系统级的备件平均备件保障概率为优化目标。在不断对库存量进行迭代的基础上,需求最大的系统平均备件保障概率,确定备件库存的最佳方案。

表4 LRU2平均备件保障概率变化数据表

表5 LRU5平均备件保障概率变化数据表
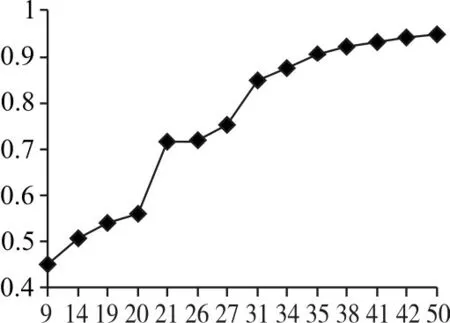
图4 备件库存预测的迭代过程
4 结语
通过改进传统的备件保障概率模型,完善备件保障概率的适用范围。指出以往系统备件保障概率的错误,对寿命服从指数分布的备件建立了库存预测模型,权衡平均备件保障概率和费用之间的关系,为备件的数量确定提供了可行的模型方法,减轻了库存压力,减少了“多存、存错”的情况。本模型是在实时送修的基础上进行的,故平均备件保障概率模型只是用于可维修性备件,对于消耗性备件是下一步研究重点。
