逆热传导问题的一种新型无网格方法
2018-10-22程秀芬
温 瑾,程秀芬
(西北师范大学数学与统计学院,甘肃兰州 730070)
0 引言
逆热传导问题出现于热物理学和连续介质力学中热传播的建模过程中.在工程应用方面,一些非破坏性评估技术是不可缺少的,根据外部分散数据来确定初始时刻的温度分布和热源,从定量分析和建模的角度来说,对该现象的研究具有很大的挑战性.在过去的许多年,很多学者已经提出了一些解决各种类型逆热传导问题的方法,如边界元方法(BEM)[1-2]、无网格高阶有限差分法[3]、基本解方法(MFS)[4-8]、径向基函数(RBFs)方法[9-11]等.但是上述这些研究都仅仅是由已知热源来确定初值或由初值来确定热源,很少同时反演热源和初值[12-14].文献[13]用基本解方法同时反演了只与时间有关的热源和初值,并且证明了解的唯一性;文献[14]用基本解方法同时反演了只与空间有关的热源和初值,并且通过对泊松方程进行适当变换,将问题化成了一个齐次的反向热传导问题和一个Dirichlet 边值问题.
近年来,随着MFS和RBFs方法的发展,Amirfakhrian等[15]将MFS和RBFs结合来确定热源,与MFS相比,MFS-RBFs得到的结果更好.Arghand等[16]将问题分为两个,然后用基本解和径向基函数相结合的方法确定热源.文中将利用上述新的无网格方法,即MFS和RBFs结合的方法来解决逆热传导问题[13].由于基本解求解的是齐次方程,文中通过MFS和RBFs 的线性组合,直接给出解的线性表达式, 然后用RBFs的线性表达式来近似热源f(t);其次,不需要使用文献[13]中的微分来计算热源,这使得本文工作更加容易.由于线性方程系统是不适定的,所以需要用Tikhonov正则化方法求解线性方程组,通过L-曲线得到最优正则化参数.
1 问题的数学表述
考虑下述逆热传导问题:
黎曼边界条件:
末端条件:
u(x,tmax)=g(x),0≤x≤L,
(4)
超定条件:
u(x0,t)=h(t),0≤t≤tmax,
(5)
这里f(t)和u0(x):=u(x,0)是未知函数,p(t),q(t),g(x)和h(t)是已知函数,x0∈[0,L],且满足相容性条件:
2 基本解-径向基函数方法
当f(t)≡0时,方程(1)可以写成下述形式:
ut=uxx,(x,t)∈[0,L]×[0,tmax].
(6)
问题(6)的基本解为
(7)
其中,H(t)为Heaviside函数.假设T>tmax是一个常数,函数
φ(x,t)=F(x,t+T)
(8)
仍然是方程(6)在区域[0,L]×[0,tmax]上的非奇异解.
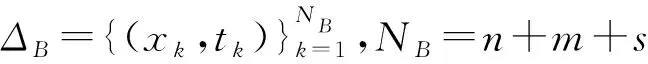
文中配置点和源点的选取是一样的.
接下来给出问题(1)~(5)的数值解法.首先,给出问题(1)~(5)的近似解:

由(9)式知N=NB+NI,我们将近似解u*强加到给定的方程,并且在任一点(x,t)∈ΔB∪ΔI处u* 满足已知条件(2)~(5).因此,将(9)式改写成如下形式:
Aλ=b,
(10)
其中,
矩阵A由(2)~(5)式定义为
(11)
其中

表1 一些常用的径向基函数
3 正则化方法
由于逆热传导问题(1)~(5)是严重不适定的,方程(10)中矩阵A的条件数比较大,并且条件数随着配置点个数的增加而急剧增加,所以大多数标准的数值方法在求解矩阵方程(10)时不能得到良好的精度.文中用正则化方法来求解这类不适定问题.
事实上,数据p,q,g,h是由测量得到的,故存在误差,这就使得右端项为带有误差的向量bδ.我们用Tikhonov正则化方法[17]来求解矩阵方程(10),即求解下述极小化问题:
其中||·||表示欧几里得范数,α是正则化参数.
正则化参数α的选取对于解的精度很关键,通常用广义交叉核实(GCV)[18]和L-曲线来选取正则化参数α[19],文中采用L-曲线来选取α.
定义如下曲线:
为L曲线,并且与正则化解相对应的正则化参数α在L曲线的“拐角”取得.
利用Matlab软件包求解方程(10).把(12)式中的正则化解表示为λα*,则问题(1)~(5)的近似解u*α为
由此,可以得到初值和热源分别为
4 数值验证
下面给出2个例子来验证本文方法的可行性.计算程序都在Matlab中给出,取L=tmax=1.
为了检验数值计算结果的精确性,定义数值的均方根误差(RMSE)和相对均方根误差(RRMSE)分别为
其中,Nt是测验点的个数,u和u*分别是精确解和近似解.
例1问题(1)~(5)的精确解为:
图1给出了Tikhonov正则化方法解方程组(10)的逆热源问题所提供的L-曲线,其中,T=5,C=0.25.从图1可以观察到,当δ=0.01,0.03,0.05时,正则化参数分别为α*=1.1250×10-5,3.0677×10-4,3.9593×10-5.
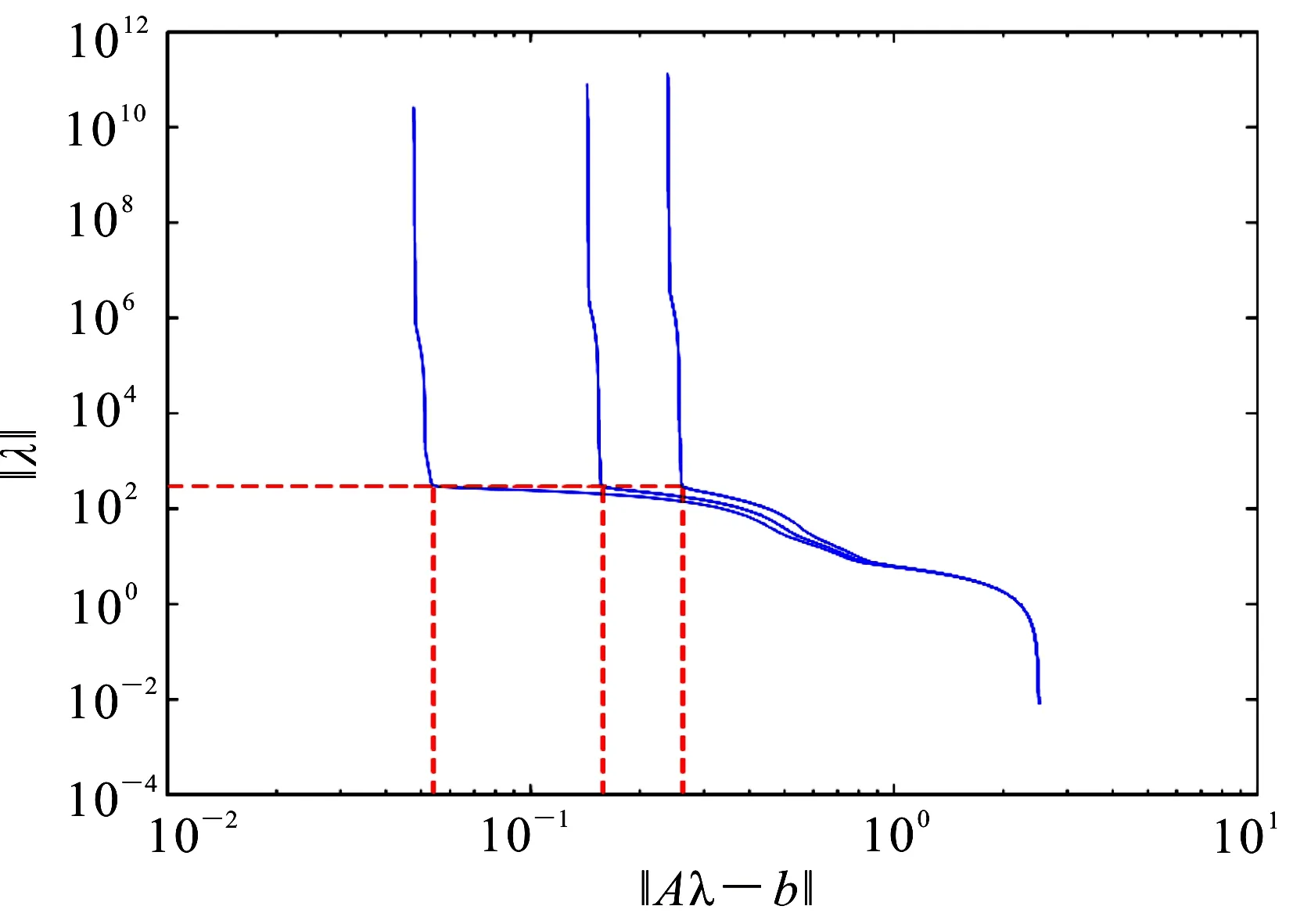
图1 不同噪音水平的L-曲线
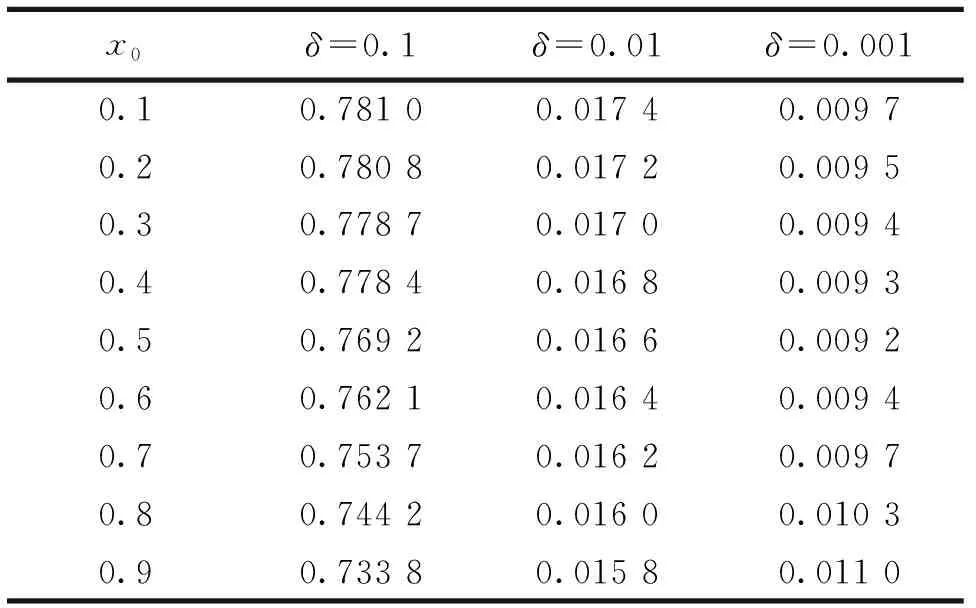
x0δ=0.1δ=0.01δ=0.0010.10.781 00.017 40.009 70.20.780 80.017 20.009 50.30.778 70.017 00.009 40.40.778 40.016 80.009 30.50.769 20.016 60.009 20.60.762 10.016 40.009 40.70.753 70.016 20.009 70.80.744 20.016 00.010 30.90.733 80.015 80.011 0
由表2,取T=5,C=0.25,n=m=s=NI=20时,x0的选取对RMSE(f)的影响很小,并且x0到中心区域的距离越近,数值解的精确性越好.
取x0=0.5,n=m=s=NI=20,T=5,C=0.25时,图2(a)和2(b)分别展示了u0(x)和f(t)在不同噪音水平下的精确解和近似解,可以看出本文提出的方法效果较好.图3给出了RMSE(u0)和RRMSE(u0)随T变化的情况,可以看出,当T≥15时误差相对稳定.
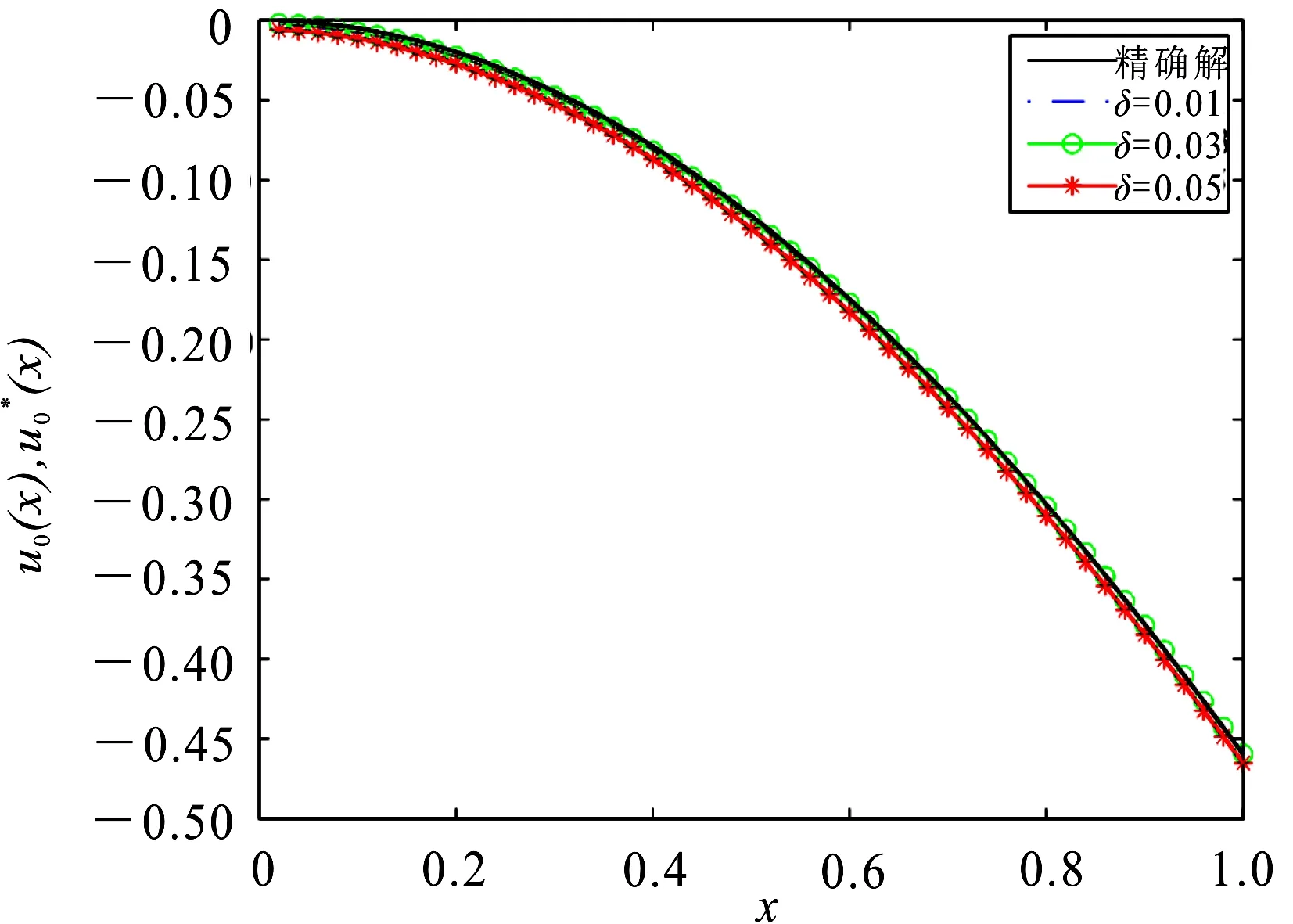
(a)u0(x)的精确解和近似解

(b)f(t)的精确解和近似解

图3 RMSE(u0)和RRMSE(u0)与T的关系
下面给出一个不光滑的例子,用有限差分格式的Crank-Nicolson公式来求解正问题的末端数据和中间点的温度分布.
例2考虑下列问题:
图4给出了上述正问题的解u(x,t).取x0=0.5,T=2,C=3,n=m=s=NI=100时,图5(a)和5(b)分别呈现了u0(x)和f(t)在不同噪音水平下的精确解和近似解,可以看出,数值近似解没有例1的效果好,但由于例2中的f(t)是一个分段函数,所以得到这样的结果也是合理的.图6中,取x0=0.5,n=m=s=NI=100,δ=0.01,C=3时,给出了RMSE(u0)和RMSE(f)与T之间的关系,可以看出,当T≤9时误差相对稳定,所以该方法在处理非光滑数值例子时效果也非常好.
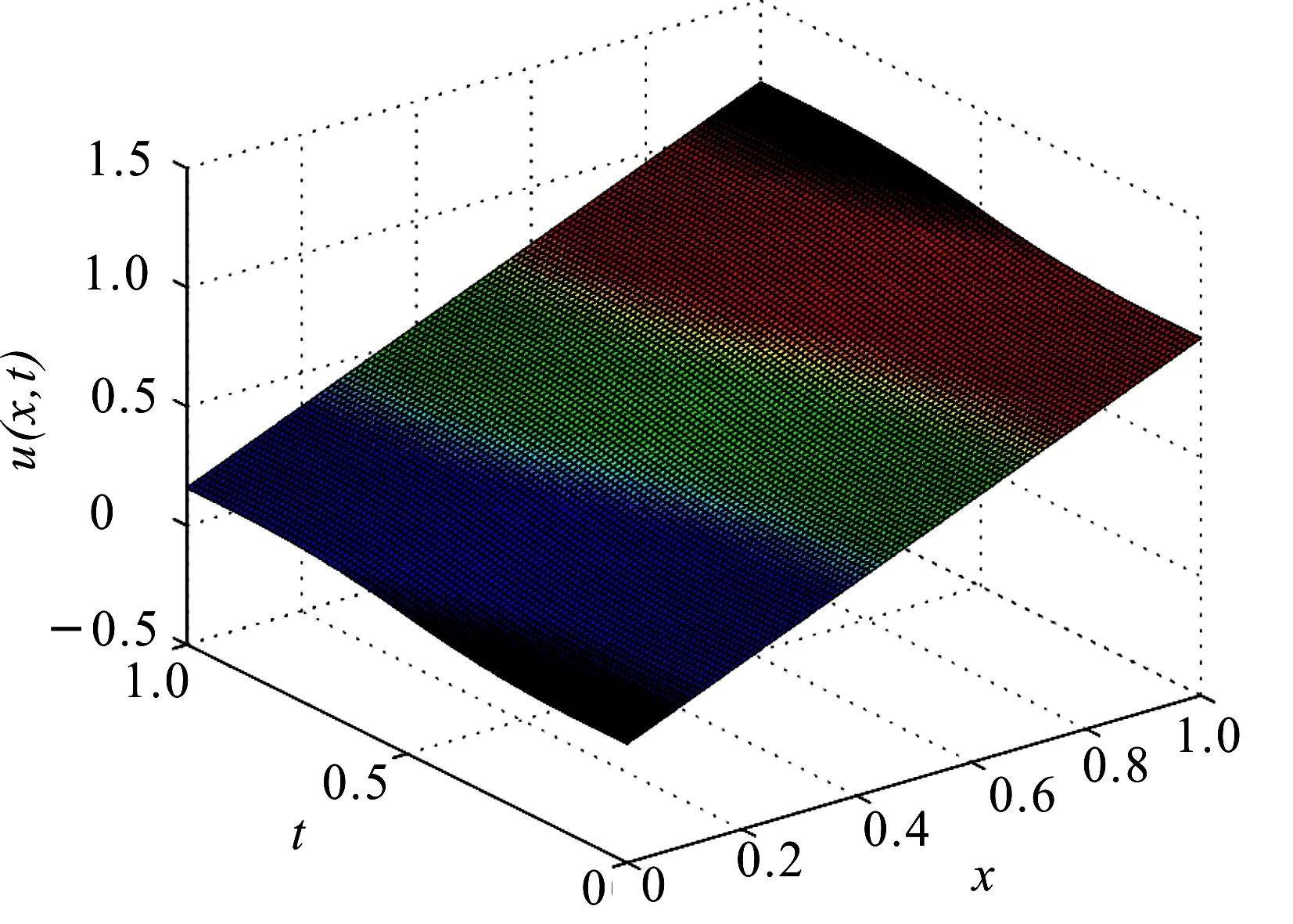
图4 正问题的解u(x,t)

(a)u0(x)的精确解和近似解
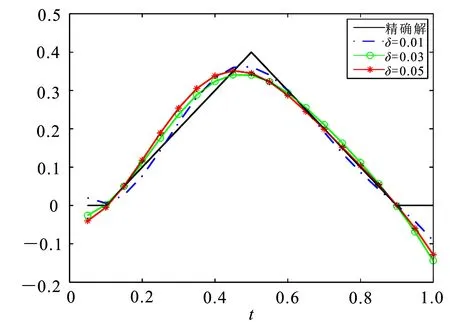
(b)f(t)的精确解和近似解

图6 RMSE(u0)和RMSE(f)与T的关系
5 结束语
文中运用了一种新的无网格方法,即基本解和径向基函数相结合的方法同时反演热源和初值.数值结果验证了该方法在解决同类型的逆热源问题的精确性和可行性,这个方法也可以推广到未来研究的其他反问题中.
