功能梯度压电层状介质中反平面运动裂纹问题分析

陆万顺，郭玉彬，马 旭，田彦山

(1.宁夏师范学院数学与计算机科学学院，宁夏固原 756000； 2.宁夏大学数学与计算机学院，宁夏银川 750021)

功能梯度夹心结构作为一种能够消除传统复合材料层合结构中由层间应力不连续导致的结构脱层失效的新型夹心结构受到了学者的大量关注.杨权权等[1]采用分层均匀化方法，给出了远场均布载荷作用卜材料参数沿孔周法线方向任意变化的FCM加强环内的复势函数解.通过数值算例，讨论了加强环内杨氏模量不同变化规律对三角形、矩形等几何形状孔附近应力分布的影响.程家幸等[2]研究了含微孔洞缺陷的压电功能梯度材料矩形板的热屈曲相关特性,推导了屈曲平衡方程，结合数值算例分析了功能梯度层材料性能的梯度参数、厚度及长宽比对临界屈曲温度的影响，最后分析了微孔洞损伤对临界外荷载的影响.张波[3]研究了微尺度各向异性功能梯度梁/板力学问题，通过若干个不同边界条件下受不同载荷作用的微结构数值算例，分析了尺度效应对各力学行为的影响，探讨了多种结构尺寸参数和材料参数对尺度效应明显程度的影响.胡统号等[4]研究了弹性边界径向功能梯度压电环板面内振动问题， 推导了弹性边界径向功能梯度压电(FGPM)环板内自由振动的控制微分方程，利用微分求积法(DQM)将控制微分方程和边界条件离散化，得到了求解频率的特征方程.通过数值求解得到了径向FGPM环板内自由振动的无量纲频率，考虑了弹性边界和电学开路组合边界条件下径向FGPM环板的梯度指数、内外径比、弹性边界的弹性刚度和压电效应对无量纲频率的影响，最后研究了径向FGPM环板模态特性. 黄志强等[5]研究了功能梯度材料热传导的统计多尺度边界元分析，针对功能梯度材料的稳态热传导问题，给出了一种基于边界元模型的统计多尺度分析方法，并针对典型问题进行了数值模拟.文献[6]研究了功能梯度材料斜裂纹动态扩展的近场动力学模拟问题，采用近场动力学理论，模拟功能梯度材料在受动态拉伸荷载作用下的裂纹扩展问题，给出了功能梯度材料的斜裂纹扩展路径及破坏形态，同时讨论材料梯度形式对裂纹扩展行为的影响.文中在渗透型电边界条件下, 应用积分变换将混合边值问题转化成对偶积分方程, 将对偶积分方程化为第二类Fredholm积分方程, 给出了应力强度因子的表达式.通过数值算例,分析了裂纹的运动速度, 梯度参数及几何比率对应力强度因子的影响.

图1 含功能梯度压电带的层状介质中粘接界面上的 反平面运动裂纹

1 问题的描述和基本方程

考虑如图1所示的问题,宽度为h2的压电夹层与厚度分别为h1与h3的功能梯度压电条和正交异性的弹性长条粘接,板两侧同时受反平面机械载荷τ0和平面电载荷D0共同作用.为方便起见,设层合板中裂纹粘接界面与静态坐标系OXYZ的X轴重合,其中压电材料沿Z轴极化.假定一长度为2a的裂纹以速度v沿着界面运动,并且在运动的过程中裂纹长度始终保持不变.

假设功能梯度压电材料中的材料常数沿Y轴呈指数变化

其中,c440,e150,ε110和ρ0分别为Y=0处压电材料的剪切模量、压电常数、介电常数和材料密度;β为梯度参数.

对于反平面问题,3种不同材料的本构方程分别为

(2)

其中，K=X,Y;ωi及φi分别为Y=0处反平面位移和电势(下标i=1,2,3,分别代表3种不同的材料);c553和c443为弹性材料的材料常数.

在忽略体积力的情况下,平衡方程为

由(1)～(3)式,可以得到反平面动力学控制方程分别为

(4)

引入Bleustein函数

(5)

则控制方程可以简化为

(6)

为了便于分析,引入Galilean变换

x=X-vt,y=Y,z=Z,

(7)

则在xyz坐标系下的控制方程为

(8)

考虑渗透型电边界条件.由于所研究问题和图形的对称性,只需考虑右半平面,即y≥0,边界条件可表示为

1)裂纹面边界条件

(9)

2)非裂纹面边界条件

(10)

2 对偶积分方程的导出

利用Fourier余弦变换及其逆变换

则控制方程(8)的解为

其中，Ai(S),Bi(S),Ci(S)和Ei(S)(i=1,2)均为未知函数;a0,b0,c0,d0,e0和f0是由边界条件确定的未知实常数,并且有

(12)～(15)式代入(5)式中，得到功能梯度压电材料和压电材料中电位移表达式

应力分量和电位移分量分别为

引入位移差函数

f(x)=ω1(x,0+)-ω1(x,0-),

(24)

进行Fourier余弦变换，则有

A1(s)+A2(s)-C1(s)-C2(s)=f(s).(25)

由边界条件可得关于Ai(s),Bi(s),Ci(s),Di(s)和Ei(S)(i=1,2)的线性方程组

通过求解(25)～(32)式,可得到如下关系式

其中N1(s),N2(s),N3(s)和N4(s)的具体表达式为

通过(33)～(37)式，最终将Ai(S),Bi(S),Ci(S),Di(S)和Ei(S)(i=1,2)的表达式均用含f(s)的式子表示出来.

由边界条件可得

由裂纹面边界条件中的混合边界条件可得对偶积分方程

(43)

其中

利用Copson-Sih方法求解对偶积分方程(43),其解为

(44)

其中J0为第一类0阶Bessel函数.

将(44)式代入方程(43),则新的函数Φ(ξ)受下面的第二类Fredholm积分方程控制

(45)

这里核M(ε,η)满足

3 裂纹尖端场的强度因子

由(19)-(20)式,可知裂纹面上的应力、电位移的表达式为[7]

其中J1为第一类1阶的Bessel函数.

得

则裂纹尖端应力和电位移奇异部分的渐近形式可表示为

反平面裂纹尖端的应力强度因子和电位移强度因子分别为

为了便于分析,分别将应力强度因子和电位移强度因子标准化为

4 数值算例和结果讨论

考虑Y=0压电材料为PZT-5;弹性材料为Graphite-Epoxy,下面主要分析梯度参数、带宽比率、裂纹长度与带宽比率及裂纹的无量纲运动速度对标准化应力强度因子的影响.

图2给出了在h1=h2=h3,且a/h1=0.1的情况下,不同无量纲运动速度v/cT1情况下梯度参数βa对标准化应力强度因子的影响.对于同一运动速度v/cT1,标准化的应力强度因子随着梯度参数βa增大而逐渐减小,并且趋于稳定;对于不同的运动速度v/cT1,速度越大标准化的应力强度因子反而越小.

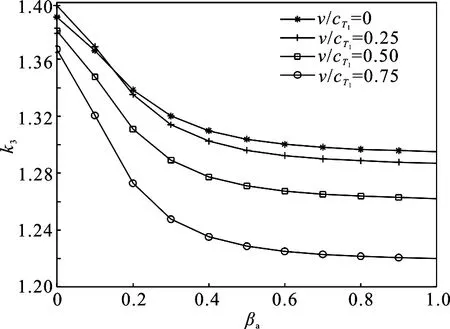
图2 不同无量纲运动速度v/cT1情况下梯度参数βa 对标准化应力强度因子的影响

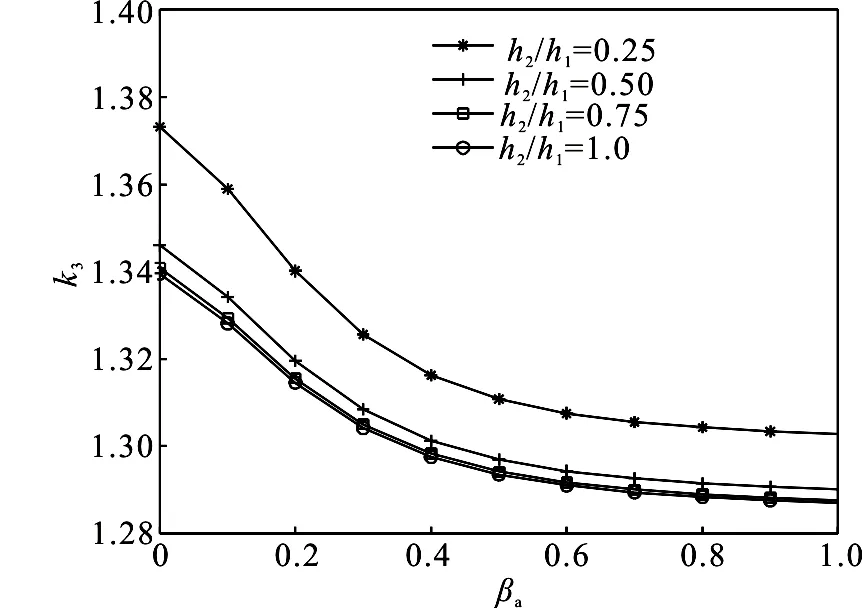
图3 不同带宽比率h2/h1情况下梯度参数βa 对标准化应力强度因子的影响

图3给出了在h1=h3，v/cT1=0.1以及a/h1=0.1时,不同带宽比率h2/h1情况下梯度参数比率βa对标准化应力强度因子的影响.对于同一带宽比率,标准化应力强度因子随着梯度参数βa增大而逐渐减小;对于不同的带宽比率,带宽比率越大标准化应力强度因子反而越小.

图4给出了在h1=h2=h3时,不同几何比率2a/h1情况下无量纲运动速度v/cT1对标准化应力强度因子的影响.对于同一几何比率2a/h1,标准化应力强度因子随着无量纲运动速度增大而逐渐减小;对于不同的几何比率2a/h1,几何比率越大标准化应力强度因子随之越大.

图5给出了不同梯度参数βa情况下几何比率h3/h1对标准化应力强度因子的影响.从图中可以看出,标准化应力强度因子随着梯度参数βa的增大而减小;随着比率h3/h1的增大而增大.

图4 不同几何比率2a/h1情况下无量纲运动速度v/cT1 对标准化应力强度因子的影响

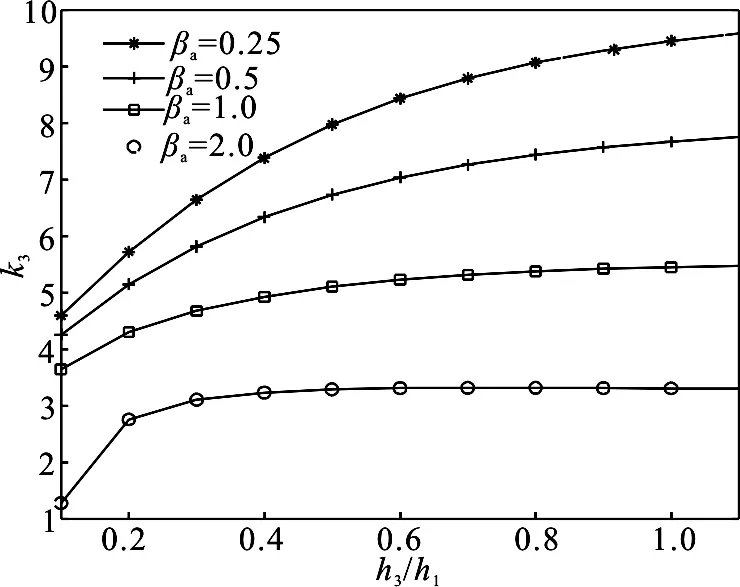
图5 不同梯度参数βa情况下几何比率h3/h1 对标准化应力强度因子的影响

5 结束语

文中研究了功能梯度压电层状介质中反平面运动裂纹问题.利用 Fourier积分变换技术,将混合边值问题归结求解的第二类Fredholm积分方程.

通过求解获得了裂纹尖端局部场的形式解的表达式,求出了粘接界面上的反平面运动裂纹的应力强度因子,分析了材料的梯度参数,几何比率和裂纹的运动速度对强度因子的影响.通过数值计算结果表明,应力强度因子随着梯度参数增大而逐渐减小；对于同一带宽比率，标准化应力强度因子随着梯度参数增大而逐渐减小；对于不同的带宽比率，带宽比率越大标准化应力强度因子反而越小；对于同一几何比率，标准化应力强度因子随着无量纲运动速度增大而逐渐减小；对于不同的几何比率，几何比率越大标准化应力强度因子随之越大.随着梯度参数参数的增大而减小;随着几何比率的增大而增大.