基于径向预紧的滚轮齿条传动力学性能研究

李 波 ，刘清蝉 ，林 聪 ，杨 明

（1.云南电网有限责任公司 电力科学研究院，云南 昆明 650217；2.中国南方电网公司 电能计量重点实验室，云南 昆明 650217）

1 引言

滚轮齿条传动机构齿条上的理论廓线为短幅摆线，实际廓线为理论廓线的等距偏移线，偏移距离为滚轮上滚柱的半径；滚轮周向均匀安装有多个滚柱，滚柱通过滚针或者轴承与滚轮连接。滚轮齿条传动机构通过滚柱在齿条齿面上纯滚动以实现位移、能量的传递，径向预紧时，传动机构能够实时消除齿侧背隙，实现精密传动，精密传动机构能够实现实时精密传动是其重要价值的体现[1]。

滚轮齿条传动机构具有高精度、高效率以及大行程，在精密传动机构中有良好的应用前景[2-3]，国内外较多学者对该传动机构进行了研究。文献[4]采用解析的方法，推导出计算重合度的方法，并建立量化重合度与齿顶圆厚度的相互关系；文献[5]通过二维制图软件对齿形进行了设计；文献[6]提出了一种通过引入齿根圆弧半径代替标准摆线齿轮根防止齿轮齿故障的新方法，对所提出的设计齿轮齿的性能进行评估；文献[7]对CF和TF弯曲强度进行了比较，CF可获得较小的压力角。

2 传动原理

滚轮齿条传动结构，如图1所示。滚轮滚圆半径为r0，滚柱半径为r。滚柱与滚轮通过滚针轴承联接。滚轮与齿条安装后，多个滚柱与齿条相切，滚轮加载径向预紧，啮合线处产生一定预紧量。滚轮作为主动件转动时，滚柱与齿条齿面啮合，并在齿条齿面纯滚动，啮合副产生的法向力推动齿条移动，实现动力输出。

图1 齿轮滚条结构简图Fig.1 Schematic Diagram of a Rolling Gear

3 法向力计算

齿条理论齿面齿面方程为：

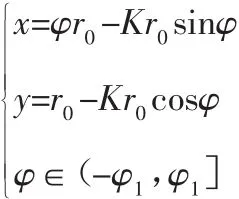
式中：K—短幅系数；

r0—滚圆半径；

n—滚柱数目，φ1=arccos［（-h+Kr0+dr/2）/（Kr0）］（单位统一）。

滚轮齿条传动机构受力分析，如图2所示。滚柱绕O点转动，建立直角坐标系XOY；δ0—径向预紧量；M0—阻力矩；Rx—滚柱分布圆半径；α—压力角；Fn—啮合法向力；φ—滚柱转过角度；l为法向力力臂；P—滚柱与齿条相对速度为0的点；R—O点与P点之间的距离。

屋里屋外到处都是碎纸片，像电影电视里逃亡前的画面。连垃圾桶都搬走了，院子里空荡荡的，只有无花果突兀地立在中间。南菜的日子，都留在无花果身上了。

加载预紧量δ0，滚柱相对齿面法向趋近量为δy。齿条运动时，滚轮受到阻力矩M0作用，产生滞后转角αz，滚柱相对齿面法向趋近量为 δz。δz与 αz之间的关系为：

其中，l=R cosα。

压力角与转角φ之间的关系为：

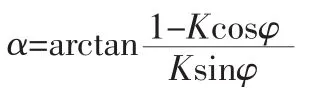
啮合线趋近量与法向力之间的非线性关系为：

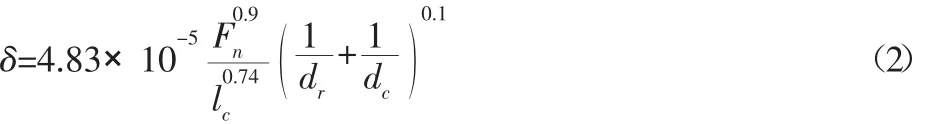
式中：lc—接触线长度；

dr—滚柱直径；

dc—齿条齿面曲率半径二倍。

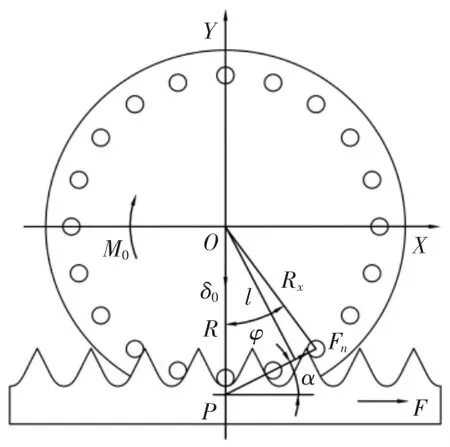
图2 受力分析图Fig.2 Force Analysis Diagram

在预紧条件下，联立式（1）、式（2）可得：

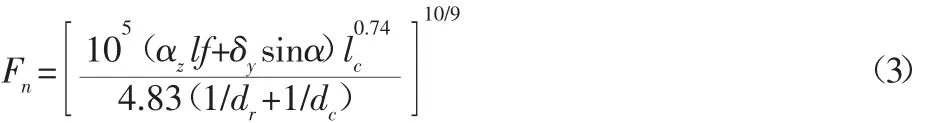
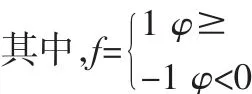
设转角为φ时参与啮合的滚柱数目为Z，第i个滚柱与齿面的弹性趋近量为δzi，根据滚柱的静力平衡条件可知：

式中：Fni—第i个滚柱法向力；li—第i个滚柱法向力作用线到O点距离。

联立式（3）、式（4）可得 αz与阻力矩 M0径向预紧 δy之间的函数关系式，通过数值分析软件进行求解。

齿条齿面曲率半径为：

啮合线上的接触应力[8]为：

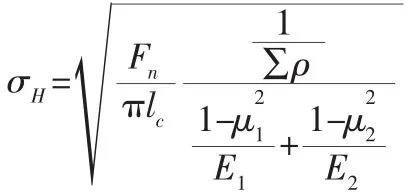
式中：μ1、μ2—滚柱、齿条的泊松比；E1、E2—滚柱、齿条的弹性模量，1/Σρ=2/d r+2/d c。

4 应力分析

齿顶需要进行修型，修型后齿高h=9mm，机构参数为滚柱直径 dr=4mm，滚圆半径 R=40mm，滚柱个数 20，φ1为 0.6342，短幅系数 K=0.9，预紧量δ0=3μm。

4.1 阻力矩对应力的影响

滚柱直径d r=4mm、预紧量δ0=3μm时，阻力矩对应力的影响，如图3所示。阻力矩分别为 0N·m、10N·m、20N·m、30N·m、40N·m时，应力随转角的变化规律，如图3所示。

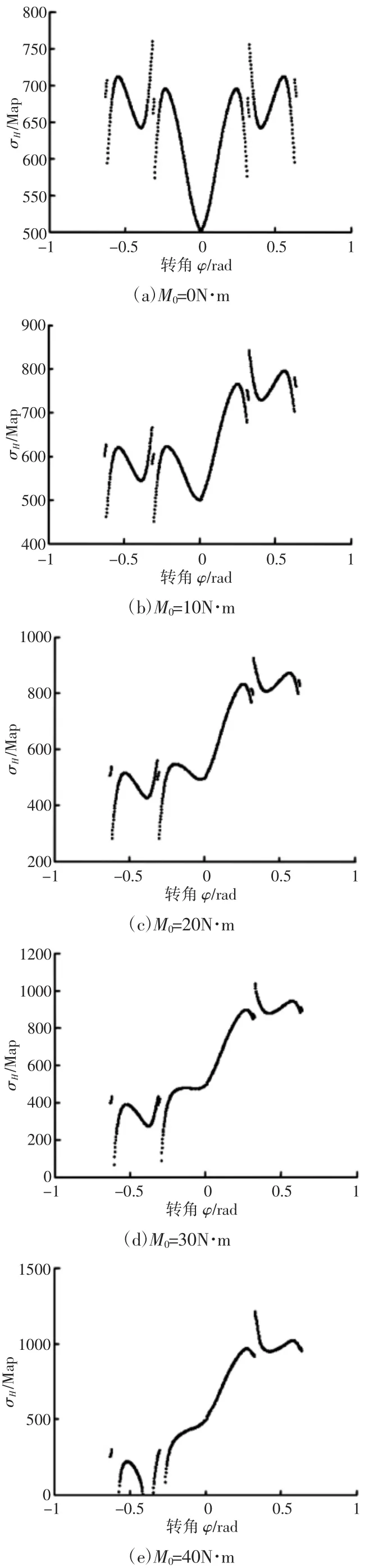
图3 阻力矩对啮合副应力的影响Fig.3 The Influence of the Resistance Moment on the Stress of the Meshing Pair

阻力矩为0N·m时，啮合副应力由径向预紧量产生，应力曲线关于φ=0对称，一周期内应力曲线出现8个断点（φ=0rad前后存在断点），最大值为761.4MPa，出现在φ=±0.3209rad处，最小值为501.6MPa，出现在φ=0rad处。阻力矩为0N·m时，加载径向预紧力后，啮合线处的啮合刚度系数不同，滚轮实现静平恒时弹性转角不为零，滚柱与齿啮入、啮出时应力曲线出现断点，则一周期内应力曲线会出现8个断点。阻力矩大于0N·m时，啮合副应力由径向预紧量和阻力矩产生。随着阻力矩增加，在区间（-φ1，0）内的啮合线应力逐渐减小，在区间（0，φ1）内的啮合线应力逐渐增加，断点对应的转角值不发生变化，最大值出现在φ=0.3209rad处，φ1为定值0.6342。阻力矩为30N·m时，前半周期应力曲线在部分区间出现零值。

4.2 滚柱直径对应力的影响

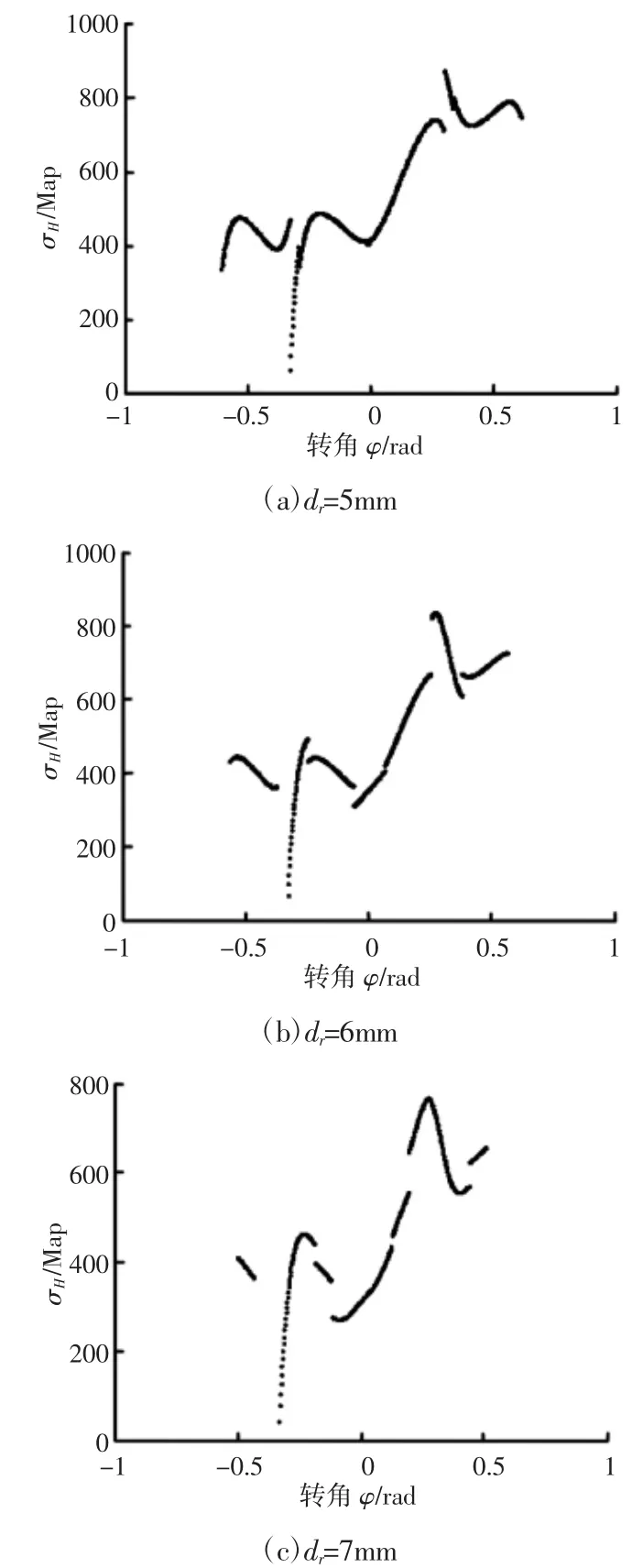
图4 滚柱直径对啮合副应力的影响Fig.4 Influence of Roller Diameter on Stress of Meshing Pair d r=5mm时，φ1=0.6104rad，应力最大值为875.7MPa，出现在φ=

阻力矩M0=20N·m、δ0=3μm时，滚柱直径对应力的影响如图4所示，滚柱直径分别为5mm、6mm、7mm时，齿高分别为9mm、8.6mm、8mm，φ1分别为 0.5054rad、0.5653rad、0.6104rad，应力随转角的变化规律，如图4所示。0.298rad处；dr=6mm时，φ1=0.5653rad，应力最大值为837.5MPa，出现在φ=0.271rad处，前半周期部分区间内应力为0；dr=7mm时，φ1=0.5054rad，应力最大值为769.5MPa，出现在φ=0.271rad处。随着滚柱直径的增加，φ1值逐渐减小，应力最大值逐渐减小，一周期内断点数为6个。

4.3 预紧量对应力的影响

阻力矩M0=20N·m、滚柱直径dr=4mm时，预紧位移对应力的影响，如图5所示。预紧量分别为0μm、1μm、2μm时，应力随转角的变化规律，如图5所示。

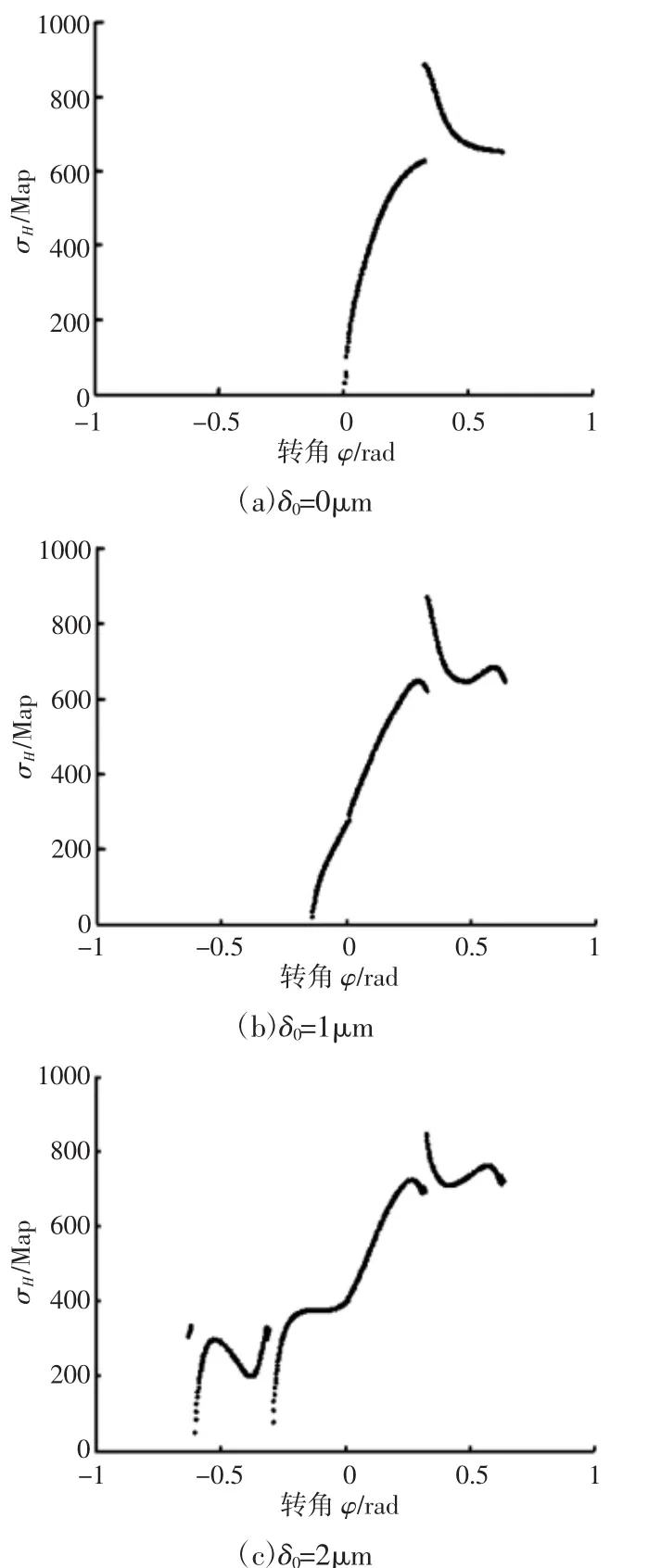
图5 预紧量对啮合副应力的影响Fig.5 The Influence of Preload on the Stress of Meshing Pair

δ0=0μm时，应力最大值为887.8MPa，出现在φ=0.3218rad处，前半周期啮合副应力为0；δ0=1μm时，应力最大值为870.9MPa，出现在φ=0.3218rad处，在区间（-0.6342，-0.1402）啮合副应力为0；δ0=2μm时，应力最大值为851.8MPa，出现在φ=0.3218rad处，在前半周期较小区间内啮合副应力为0。随着径向预紧量的增加，应力最大值逐渐减小，应力最大值所对应的转角值不变，应力为零的区间逐渐减小。

5 结论

建立啮合副受力分析模型，根据力矩平衡方程得到传动机构啮合副法向力，分析不同参数对应力的影响，得到如下结论：

（1）随着阻力矩增加，前半周期啮合副应力逐渐减小，后半周期啮合副应力逐渐增加，应力最大值对应转角为定值，应力曲线出现断点个数为定值，断点对应的转角值不发生变化。阻力矩达到一定值时，前半周期啮合副出现齿侧间隙。

（2）随着滚柱直径的增加，φ1值逐渐减小，应力最大值逐渐减小。Dr达到一定值时，应力最大值对应转角不发生变化，一周期内断点数减少。

（3）随着径向预紧量的增加，应力最大值逐渐减小，应力最大值所对应的转角值不变，前半周期应力为零的区间逐渐减小。