偏心运动双平面超精研抛圆柱面研究

姚蔚峰 袁巨龙 江 亮 冯凯萍 陈 锋

1.绍兴文理学院机械与电气工程学院，绍兴，312000

2.浙江工业大学超精密加工研究中心，杭州，310014

3.西南交通大学材料先进技术教育部重点实验室，成都，610031

4.衢州学院机械工程学院，衢州，324000

5.浙江方圆检测集团股份有限公司，杭州，310018

0 引言

圆柱滚子是滚动轴承的滚动体，由于其与滚道之间为线接触，具有承受高负荷的能力，特别适用于重载并高速旋转的机械装备，如高速机床主轴［1］、风力发电机［2］、轨道机车［3］等。圆柱滚子的形状精度［4］、表面质量［5-6］及其一致性［4，7］对轴承的运动精度和使用寿命会产生很大影响。

目前，轴承圆柱滚子的批量生产终加工手段以无心磨削最为广泛，但是无心磨削在原理和工艺上也存在诸多问题，限制了工件加工精度及其一致性的提高，如砂轮和导辊在加工过程中持续磨损使得工件加工条件不一致，易造成砂轮表面损伤，高度依赖设备部件的精度和刚性，各个零部件的位置和角度调节操作难度大等。YUAN等［8］针对目前我国轴承圆柱滚子加工技术存在的加工精度低、批一致性差等问题，提出了双平面圆柱外圆加工方法，即将半导体元件超精密加工行业广泛应用的双平面研磨抛光方法应用于轴承圆柱滚子外圆的批量超精加工，利用其进化加工、误差匀化、加工轨迹均匀性良好等优点来获得工件外圆的高形状精度、高表面质量及其高一致性。

本文采用偏心运动双平面加工方式实现圆柱面的超精研抛，以提高圆柱面的形状精度和表面质量。结合理论、仿真和试验手段，从几何运动学角度对圆柱面加工轨迹形态和工件表面微观形貌进行研究，分别分析了工件中心至夹具中心距离与夹具中心至研磨盘中心距离的比值、夹具自转转速与夹具公转转速的比值对加工轨迹形态和轨迹交叉角度的影响规律，最后进行轴承滚子圆柱面超精研抛试验。

1 加工原理

偏心运动双平面超精研抛圆柱面的加工原理如图1所示，其执行构件主要包括上盘、下盘、带齿环形夹具、偏心轮和齿圈。偏心轮几何中心与上下盘转轴中心存在偏心距，带齿环形夹具中心开孔可以套在偏心轮上，夹具几何中心与偏心轮几何中心重合，夹具圆周的外齿与齿圈啮合。

加工时，在加工载荷作用下，平行、平整的上下盘将一批圆柱工件压住，上下盘定轴转动，夹具在齿圈和偏心轮共同驱动下绕盘转轴做公转运动，并绕自身几何中心做自转运动，在上下盘和夹具的共同作用下，圆柱工件做摆线式平移并同时滚动。研磨或抛光液从上盘的孔隙流道输送至圆柱工件与上下盘之间的接触区域，由于上下盘、磨粒和圆柱工件之间存在相对运动，因此可实现磨粒对工件圆柱面材料的去除。高度平整的上下盘和较均匀的加工轨迹分布是获得高精度圆柱面轮廓的重要保证。

2 加工过程几何运动学分析

图1 偏心运动双平面超精研抛圆柱面的加工原理Fig.1 Schematic of both-sides cylindrical lapping and polishing process in eccentric rotation

工件与工具之间发生相对运动是工件表面产生材料去除和几何轮廓成形的关键影响因素之一，因此分析加工过程中工件的几何运动学是加工制造领域重要的理论分析手段，它可以揭示工件表面材料去除和几何轮廓成形的规律［9］。

依据图1所示的加工原理，下文基于几何运动学对偏心运动双平面超精研抛圆柱面建立加工系统数学模型。设置如下假设：圆柱工件定义为理想圆柱体；忽略加工过程中由于摩擦不稳定导致的滑动；上下盘的摩擦因数相同，圆柱工件与下盘做纯滚动，受上盘影响不大［8］；上下研磨盘盘面均为理想平面，且均平行于地面；圆柱工件与研磨盘接触为刚性线接触。

2.1 坐标系统建立和参数定义

加工过程中夹具绕研磨盘转轴做公转运动，圆柱工件随夹具一起绕夹具中心做自转运动，同时圆柱工件做滚动，依据这一运动特点建立加工系统坐标，如图2所示。首先建立全局坐标系OXYZ，定义原点O为下盘转轴中心，X轴和Y轴构建了一个固定于地面且与研磨盘面平行的OXY平面，Z轴垂直于OXY平面。在OXY平面上定义夹具中心Oc和圆柱工件中心Or，在加工初始时刻，点Oc和点Or均位于X轴上。在圆柱工件中心Or建立局部坐标系OrMN，其中，M轴方向为圆柱滚动方向，N轴方向为圆柱轴线方向，两者相互垂直。依据圆柱工件与下盘接触并发生纯滚动［8］，且研磨盘面与OXY平面平行，定义圆柱工件中心Or在研磨盘面上的投影点A为点Or所在圆截面与下盘的接触点，在Z轴方向上两点重合。

图2 加工系统坐标建立和参数定义Fig.2 Coordinate system，geometric and kinematic parameters of processing system

2.2 几何运动学分析

在实际加工中，夹具的公转转速和自转转速均可得到确定的控制，故夹具公转角速度ωco和夹具自转角速度ωrc为已知量。那么经过加工时间t后，得到夹具公转角度φco和夹具自转角度φrc分别如下：

如图2所示，坐标原点O、夹具中心Oc、圆柱工件中心Or组成三角形△OOcOr，根据余弦定理可得点Or至点O的距离Lro和角度φ2（即∠OrOOc）：

式中，Lco为点Oc至点O的距离；Lrc为点Or至点Oc的距离。

已知研磨盘转动角速度ωa，那么接触点A处研磨盘的线速度vAo的模可表示为

则夹角中心Oc相对下盘中心O公转的线速度矢量vco和圆柱中心Or相对夹角中心Oc自转的线速度矢量vrc的模可分别由下式获得

为了分析圆柱工件的滚动状态，在接触点A处定义圆柱工件的滚动线速度矢量，如图2所示，则圆柱工件滚动角速度矢量模|ωroll|由下式获得：

图3 各速度矢量的几何关系Fig.3 Relationships between velocity vectors

根据速度矢量分析法，将速度矢量vAo、vco、vrc、整理到坐标系O′X′Y′建立几何关系，如图3所示。将夹具公转线速度vco所在方向设定为X′轴，O′X′Y′坐标原点O′设定为vco的起始点，Y′轴垂直于X′轴，圆柱工件局部坐标系OrMN也变换到O′X′Y′坐标系中。由于圆柱中心Or所在圆截面与下盘接触于点A并发生纯滚动［8］，因此建立如下关系式：

则将式（11）代入式（9）变换为

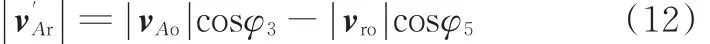
式中，φ3为速度矢量vAo和的夹角；φ5为速度矢量vro和的夹角。

前文已求解|vAo|，下文将分别求解|vro|、φ3和φ5。

定义速度矢量vco的坐标为（ωcoLco，0），则速度矢量vAo和vrc的坐标表示为

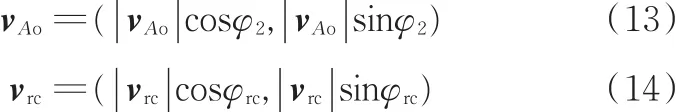
将速度矢量vrc和vco相加得到速度矢量vro：

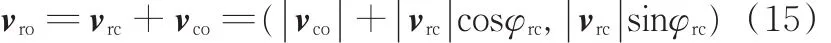
则速度矢量vro的模为

根据图3所示各速度矢量几何关系，可得角度φ3、φ4、φ5分别如下：

式中，α为圆柱工件轴线与夹具径向的夹角；φ4为速度矢量vrc和vco的夹角。

重新整理式（17）和式（19），得

最后，将式（5）、式（16）、式（20）和式（21）代入式（12）得到速度矢量模|v′Ao|，再将其代入式（8）即可得到圆柱工件滚动角速度模|ωroll|。

3 圆柱面加工轨迹仿真方法

3.1 研磨盘离散化

在偏心运动双平面超精研抛圆柱面的加工过程中，由于圆柱工件与研磨盘之间为线接触，加工区域是个面域，传统分析方法难以解释圆柱工件与研磨盘之间的相对运动关系以及实现加工轨迹仿真和定量评价，因此本文将研磨盘离散化处理，划分为若干个同心等间距圆环，这样原来工件圆柱面与研磨盘的线接触转换为圆柱面与圆环的点接触，这些接触点在工件圆柱面上形成的轨迹即为加工轨迹。

3.2 加工轨迹点的坐标计算

圆柱工件与研磨盘离散化后的圆环接触于一点，圆柱工件、研磨盘圆环和接触点的几何运动关系如图4所示，全局坐标系与图2相同。

图4 圆柱工件、研磨盘圆环和接触点的几何运动关系Fig.4 Geometric and kinematic relationships between contact point，roller and divided circles on plate

从Z轴方向视图观测，圆柱工件的轴线与所接触的圆环相交于点T，随着加工时圆柱工件不断运动，交点T的位置以及其所属圆环也在不断变化。因此，仿真时需判定圆柱工件与指定圆环是否接触，判定关系如下：

其中,Lto为点T至研磨盘中心O的距离；∠TOcO为夹具自转角度，可由下式计算获得

由三角形余弦定理建立如下关系：

求解上述方程得到点T至夹具中心Oc的距离Ltc：

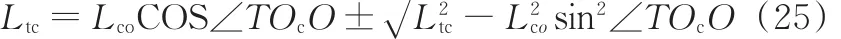
则点T在圆柱轴线方向的位移Ltr由下式获得：

其中，Ltr的解有2个，分别对应圆柱轴线无限延长后与圆环的2个交点T1、T2，然而由于圆柱工件的长度有限，因此这2个交点是否为实际接触点，还需采用如下方法进行判定（Lr为圆柱长度）。

（1）若|Ltr|＞Lr/2，此时点T在圆柱长度以外，因此相对应的Ltr值无效，在计算时删除。

（2）若|Ltr|＜Lr/2，此时点T在圆柱长度以内，因此相对应的Ltr值有效，在计算时保存。

此外，圆柱工件滚动角度θroll由下式获得：

结合Ltr和θroll，在以圆柱中心Or为原点的局部坐标系统中，接触点T在圆柱面上运动的位置坐标可由下式描述：

工件圆柱面加工轨迹即是由上述不同研磨盘圆环上的接触点T随时间运动绘制而成的。

4 仿真结果与分析

4.1 距离比对轨迹形态的影响

为便于分析关键机构尺寸参数Lrc和Lco的相对关系对加工轨迹的影响，定义距离比KL，即

其中，当KL＞1时，加工机构为偏心运动；当KL≤1时，加工机构为行星运动。

设置仿真参数如下：圆柱半径r=10 mm，偏角α=10°，下研磨盘转速ωa=20 r/min，夹具自转转速ωrc=-80 r/min，夹具公转转速ωco=18 r/min，Lco与Lrc的和为170 mm，距离比KL为{0.25，0.5，1，2，4}，则不同距离比KL条件下的工件圆柱面加工轨迹二维展开图见图5。由图5可知，不同距离比KL的工件圆柱面加工轨迹形态主要呈现织网状，轨迹在一定角度范围内相互交叉，但交叉规律各不相同。行星运动的轨迹弯曲曲率相对较大，偏心运动的轨迹弯曲曲率相对较小。

定义轨迹切线倾角θ＞0°时轨迹方向为正向，θ＜0°时轨迹方向为反向，那么定义正向轨迹切线倾角θ正均值与反向轨迹切线倾角θ负均值之差为轨迹平均交叉角度，以便于对轨迹的织网状几何形态进行定量描述。对应图5所示加工轨迹，不同距离比KL的轨迹切线倾角如图6所示，与其相对应的轨迹平均交叉角度约为{129°，130°，135°，150°，166°}。由图6可知，随着距离比KL增大，轨迹切线倾角θ偏差逐渐递减，但是对于行星运动（KL＜1时），轨迹平均交叉角度变化很小，而对于偏心运动（KL＞1时），轨迹平均交叉角度则增大很多。

图5 不同距离比KL的圆柱面加工轨迹二维展开图Fig.5 Trajectory on cylindrical surface for different ratios KLof distances

综上分析得知，相对于行星运动，距离比KL对偏心运动的轨迹形态影响更大。

图6 不同距离比KL的轨迹切线倾角θFig.6 Tangent angles θ of trajectory curves for different ratios KLof distances

4.2 转速比对轨迹形态的影响

为便于分析夹具自转转速ωrc和公转转速ωco的相对关系对加工轨迹的影响，定义转速比Kω，即

设置仿真参数如下：机构尺寸Lco=30 mm，Lrc=125.25 mm，夹具公转转速ωco=18 r/min，转速比Kw为{-4，-2，-1，-0.5，0，0.5，1，2，4}，其他参数同上。不同转速比Kω下的工件圆柱面加工轨迹二维展开图见图7，其分别对应的轨迹切线倾角如图8所示，其分别对应的轨迹交叉角度平均约为{167°，169°，172°，174°，165°，80°，142°，156°}。由图8可知，当转速比Kω=1时，轨迹平均交叉角度最小，但轨迹切线倾角θ偏差最大；当Kω＜1时，轨迹平均交叉角度较大，轨迹切线倾角θ偏差较小，轨迹形态近似，说明Kω的影响相对较小；当Kω＞1时，随着Kω值增加，轨迹平均交叉角度增大，而轨迹切线倾角θ偏差减小，轨迹形态差异较大，说明Kω的影响较大。

图7 不同转速比Kω下的圆柱面加工轨迹二维展开图Fig.7 Trajectory on cylindrical surface for different ratios Kωof speeds

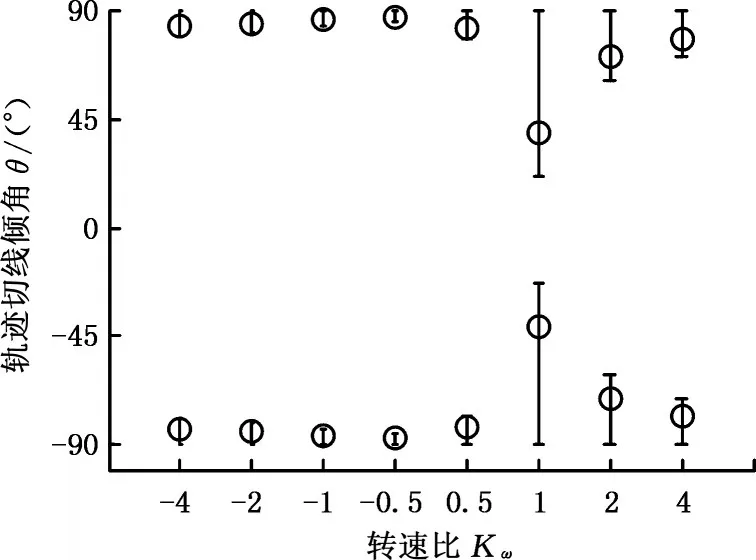
图8 不同转速比Kω的轨迹切线倾角θFig.8 Tangent angles θ of trajectory curves for different ratios Kωof speeds

5 轴承滚子圆柱面超精研抛试验

以尺寸为ϕ20 mm×30 mm的轴承钢GCr15圆柱滚子为加工对象，在自主研制的偏心运动双平面超精研抛试验装置（图9）上进行超精研和抛光试验。超精研旨在快速去除工件材料，获得工件圆柱面的高尺寸精度和形状精度，并大幅改善工件圆柱面表面质量；抛光旨在进一步改善工件的表面质量。加工试验中，机构尺寸Lrc=125.25 mm，Lco=30 mm；设置下盘转速为20 r/min，上盘转速为-8 r/min，夹具自转转速为-80 r/min，夹具公转转速为18 r/min。

5.1 超精研试验

选取平均粒径为（1.2±0.2）μm的Al2O3微粉为磨料，按17%的质量分数和水混合配制成超精研液，并添加2%（质量分数）的微乳化水溶性切削液和1%（质量分数）工业清洗剂。设置加工载荷为每个工件10 N，总加工时长为60 min，每隔10 min把工件依序取出测量再继续加工。

图9 偏心运动双平面超精研抛圆柱面的试验装置Fig.9 Experimental setup of both-sides cylindrical lapping and polishing process in eccentric rotation

采用三丰（Mitutoyo）RA-1500型圆度仪进行测量，一批工件圆柱面圆度的变化如图10所示，最后其平均值降至0.43 μm，偏差为0.14 μm，最小达到0.340 μm。采用三丰（Mitutoyo）SJ-410型表面粗糙度仪进行测量，一批工件圆柱面表面粗糙度Ra的变化如图11所示，最后其平均值降至45 nm，偏差为7 nm，最小达到42 nm。采用基恩士（KEYENCE）VHX-2000型超景深三维显微系统对工件圆柱面微观形貌进行观测，超精研60 min后，圆柱面中心位置（距离圆柱工件端面约15 mm处）的观测结果如图12a所示，实际切削痕迹的平均交叉角度约为124°。在相同加工条件下，对图12a中虚线框区域（200 μm×200 μm）进行加工轨迹仿真，仿真结果如图12b所示，仿真轨迹平均交叉角度约为151°。

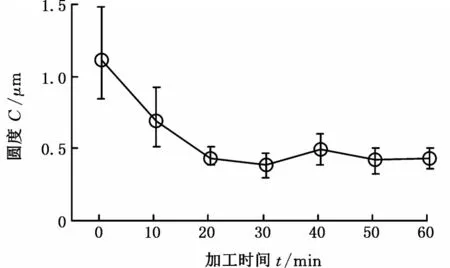
图10 超精研后圆柱面圆度的变化Fig.10 Variation of roundness of cylindrical surface with time after lapping

图11 超精研后圆柱面表面粗糙度Ra的变化Fig.11 Variation of cylindrical surface roughness Ra with time after lapping

将图12b所示仿真加工轨迹形态与图12a所示工件实际表面微观形貌进行对比，从对比结果可以看出，虽然仿真加工轨迹形态与实际表面加工痕迹形态仍存在较大误差，但总体上，仿真加工轨迹形态可以反映出实际加工痕迹相互交错呈现织网状的几何特征。

5.2 抛光试验

在前文超精研试验结果基础上，对工件圆柱面继续抛光试验。试验分为两个阶段，粗抛旨在保持较高的材料去除率并快速减小表面粗糙度，精抛旨在获得最佳的表面质量。采用JIANG等［10］开发的轴承钢化学机械抛光液，配制时pH值为4.0，其成分配比如表1所示。

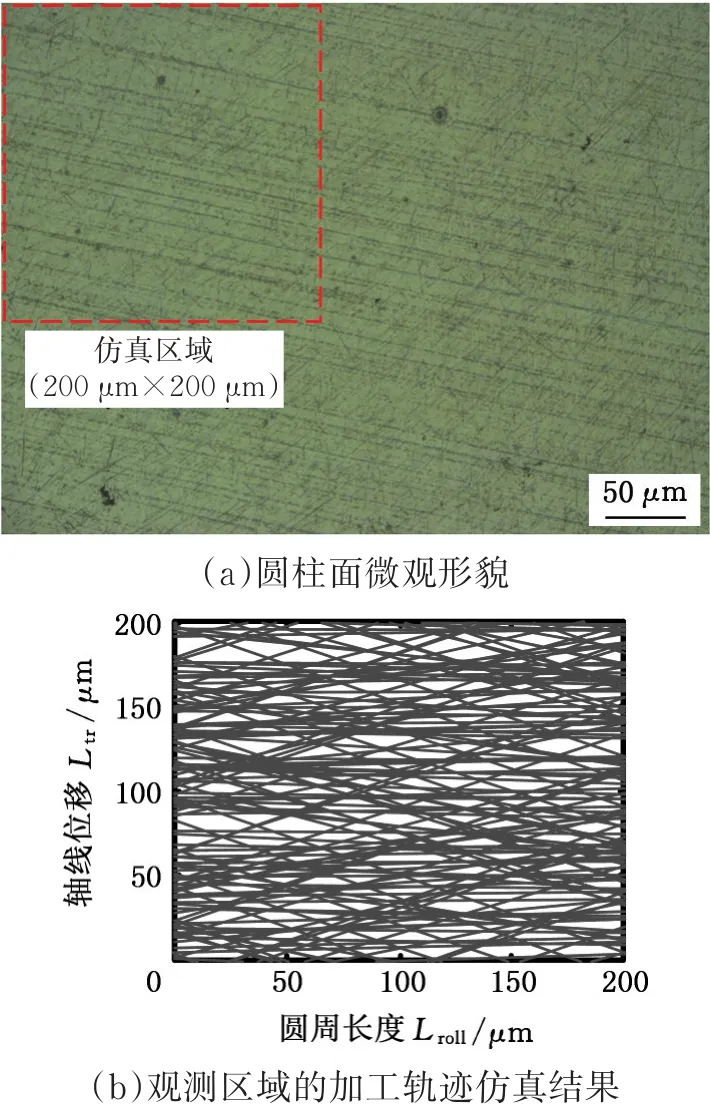
图12 超精研后圆柱面微观形貌与加工轨迹仿真的比较Fig.12 Comparison between cylindrical surface topography after lapping and simulation results of trajectory

抛光时，上下两个抛光基盘的材料采用304不锈钢，以避免被化学机械抛光液腐蚀，且基盘上贴有美国陶氏化学IC1010/Suba-IV型聚氨酯化学机械抛光垫。加工载荷为每个工件5 N。粗抛和精抛各进行10 min。

表1 轴承钢的化学机械抛光液成分配比（质量分数）Tab.1 Compositions of chemical mechanical polishing slurry for bearing steel（mass fraction）%

精抛后工件圆柱面圆度得到略微改善，圆度平均值降至0.36 μm，圆度偏差为0.13 μm，圆度最小值达到0.295 μm；表面质量得到大幅改善，表面粗糙度Ra平均值降至9 nm，偏差为4 nm，最小达到8 nm。工件圆柱面外观照片见图13，达到了镜面效果；表面微观形貌如图14所示，其中条状加工痕迹已大幅消除，同时伴有规律的散布点状微凹坑，说明抛光时材料去除以化学反应和SiO2磨粒滚压为主，伴随少量微切削，体现为三体磨损形式。

图13 精抛后工件圆柱面外观照片Fig.13 Photograph of cylindrical roller after fine polishing

图14 精抛后工件圆柱面微观形貌Fig.14 Cylindrical surface topography of roller after fine polishing

6 结语

依据偏心运动双平面超精研抛圆柱面的基本原理，基于几何运动学建立了加工系统数学模型，应用速度矢量法求解和计算了圆柱工件的各个运动状态，进而进行了工件圆柱面加工轨迹的仿真。加工轨迹形态的仿真结果可反映实际工件表面微观加工痕迹呈现出的织网状、相互交叉的几何特征，对实际工件表面形貌的分析和预测具有一定的参考价值。

结合仿真加工轨迹形态和轨迹平均交叉角度计算进行比较分析，偏心运动和行星运动的轨迹形态均呈现织网状，但轨迹交叉规律不同。相对于行星运动，机构尺寸相关的距离比KL对偏心运动的加工轨迹形态影响更大。夹具公转和自转相关的转速比Kω对加工轨迹形态的影响也较大，尤其Kω＜1时和Kω＞1时呈现出明显不同的影响规律。

在自制试验装置上对轴承钢GCr15圆柱滚子进行了超精研和抛光试验。一批工件的圆度平均值及其偏差，和表面粗糙度Ra平均值及其偏差都明显减小了，圆度最小值达到0.295 μm，表面粗糙度Ra最小值达到8 nm，表面质量可达到镜面效果。