一种基于最小条件的线轮廓度误差评定方法

陆辛成 黄美发 唐哲敏 钟艳如

1.桂林电子科技大学机电工程学院，桂林，541004

2.桂林电子科技大学计算机与信息安全学院，桂林，541004

0 引言

在大型船舶、航空和航天等领域，常常需要评定自由曲线的加工质量，因此，线轮廓度误差的准确评定有着重要的意义。由于自由曲线的特殊性，使其有时难以通过简单的几何方程来表示，此外，根据国家标准GB/T 1958-2004，形状公差的评定需要满足最小条件。在曲线轮廓度的评定中存在两大难点：一是求算测量点到理想曲线的最短距离，二是调整测量点与理想曲线的相对位置以满足最小条件。在现有的曲线轮廓度误差评定方法中，大多是将曲线切分为一系列可近似为直线的曲线段，以点到直线的距离来代替点到曲线的距离进行计算［1-3］。

求算最短距离的方法主要有分割逼近［4］、粒子群搜索［5］、构造近似曲线［6］等。调整测量点位姿的优化算法主要有遗传算法［3］、拟牛顿算法［7］、禁忌搜索算法［8］等。但现有方法仍然存在两个问题：①搜索算法效率有待进一步提高；②搜索算法的全局性难以保证，容易陷入局部解的情况。为解决上述问题，本文提出一种模拟实际量具测量过程，满足最小条件的曲线轮廓度误差的评定方法。该方法通过分析全局测点特性，快速寻找可能满足最小条件的特征点，然后模拟给定轮廓边界的收缩过程，使所有测量点最终都处于最小包容区域内，最后求算轮廓边界的间距来进行曲线轮廓度误差的评定。

1 线轮廓度公差带的定义与分析

线轮廓度公差用于控制平面曲线轮廓的形状公差，是实际轮廓线所允许的变动全量，线轮廓度公差带是包络一系列圆（直径为公差值t）的两包络曲线之间的区域，各圆圆心应位于理想轮廓曲线上［9］见图1，其中被测实际轮廓线上的离散测量点必须位于包络一系列圆的两包络曲线之间。

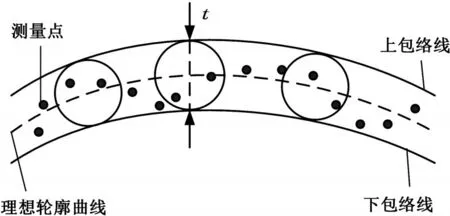
图1 线轮廓度公差带的定义Fig.1 Defination of line proflie tolerance zone

根据定义，在线轮廓度误差的评定过程中，保持所有测量点之间相对位置不变，即把实际轮廓作刚化处理，刚化的轮廓相对于上下两包络线或包容边界进行旋转和平移，每一步的搜索都要使离散测量点与包络线接触，并使两包络线之间的距离逐渐减小，直至两者间的距离为最小，此时满足了最小条件。

根据刚体运动学原理，对最小区域的搜索实际上是一个有明确指向性的逼近过程，不会陷入局部优化解的情况，理论上具有更高的计算效率。

2 理想曲线轮廓数学模型

线轮廓度误差的评定需要构建理想轮廓作为后续评定的参照，理想轮廓可以通过插值拟合来实现。目前，常用的曲线拟合方法有Bezier法、B样条和非均匀有理B样条（NURBS）。由于NURBS在IGES、STEP和PHIGS等标准中广泛使用［10］，因此本文中的理想轮廓选用NURBS曲线来建立。

2.1 曲线数学模型的构建

对于理想曲面数学模型的描述通常是通过插值拟合理想点来实现。一条p次的NURBS曲线可以表示为一分段有理多项式矢函数［10］：

其中，Pi为曲线上的控制点，这些控制点形成控制多边形来约束曲线的形状，见图2；ωi为权因子，首末权因子ω0、ωn＞ 0，其余ωi≥ 0，且按顺序排列的p个权因子不同时为0，以防止分母为零、保留凸包性及曲线不因权因子而退化为一点［11］；Ni,p(u)表示定义在非周期且非均匀节点矢量U上的p次B样条基函数，函数形式及计算方法依据de Boor-Cox给出的基函数递推式［10］：

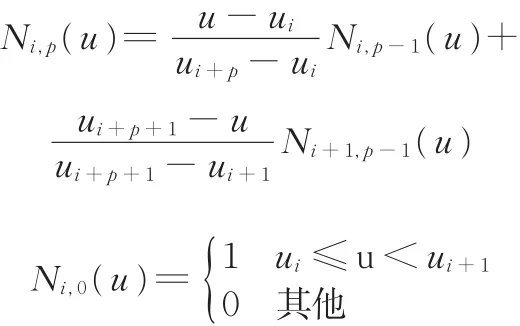
图2 控制点约束曲线形状（p=3）Fig.2 Control point constraint curve shape（p=3）

计算过程中，上式可能会出现0/0，规定0/0=0。节点矢量的表达式如下：

式中,m为控制点数。

通常将两端节点的重复度设为p+1。参数u的取值范围为［a，b］，在多数实际应用过程中设定a=0，b=1。

令

则式（1）可写为

其中，Ri,p(u)表示有理基函数，是u∈［0，1］上的分段有理函数［10］。

2.2 确定NURBS曲线的阶次

NURBS曲线由一系列基函数组合而成，为了保证曲线各连接处具有足够的光滑度，参数曲线需要满足一定的连续性，以符号Gn表示。一般情况下，拟合得到的曲线至少要满足G2连续性［11］，即曲线连接处存在关于弧长的二阶导矢，使得该点二阶可微，根据n=p-1可知NURBS曲线为3次曲线。

2.3 NURBS曲线的局部修改性

考虑到NURBS曲线存在局部修改性，即移动控制点Pi或改变权因子ωi，仅会影响到对应区间u∈［ui，ui+p+1］内的曲线形状。为简便起见，可令对所有的i，均满足ωi=1，则对所有的i，均满足Ri，p（u）=Ni，p（u），即完全通过控制点来实现曲线形状的调整。

当节点矢量处于不同区间时，有理基函数Ri，p（u）有如下形式：

其中，Bi，p（u）表示p次的伯恩斯坦基函数，其二项式递推式如下：

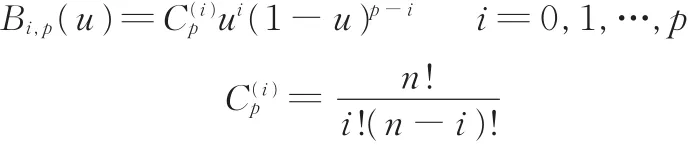
3 模拟接触法计算最小距离

在公差建模领域中，常用到小位移旋量（small displacement torsor，SDT）理论的观点，该理论存在两个前提假设：刚体假设和小变动假设。假设零件的刚性足够大，其表面形变远小于公差值，可忽略不计，且零件的公差值相对于名义尺寸是极小量［12］，因此在评定过程中，测点只会在极小的范围内变动，该范围内的两包络线段的曲率半径极大，曲率值极小，可看作相互平行的两条直线段，见图3。此外，对于平行的包络线段，在向理想曲线收缩的过程中，可能产生的弯曲变形可忽略不计，认为其始终保持平行并同时平行于对应的理想曲线段。

图3 测点运动范围内近似直线的包络线Fig.3 The envelopes of approximate straight lines in the range of motion of measuring points

假设测量区域内的三点Qi、Qi+1和Qi+2，虚线框表示测点附近的微小变动区域，则区域内的包络边界Li、Li+1和Li+2可看做直线（图3），上下边界逐渐向理想曲线收缩，上边界与Qi+2接触，此时接触点在边界的推动下沿边界Li+2的法向矢量Cn（ui+2）移动。由于当前仅有一个接触点，可令其余测点均沿Cn（ui+2）平动。

当边界收缩一段距离后使得Qi+1与下边界接触（图4），此时的上下包络边界的间距小于图3的上下包络边界的间距。接触点Qi+1在下边界的推动下沿Li+1的法向矢量Cn（ui+1）运动，由于Cn（ui+1）和 Cn（ui+2）的方向不同，因此所有测量点将以Qi+1和Qi+2连线上的一点为旋转中心进行转动。

图4 测点在边界推动下的转动Fig.4 The rotation of measuring points driven by the boundary

当旋转至Qi与上边界接触时（图5），3个测量点之间的位置关系满足国家标准GB/T 1958-2004中描述的终止条件，测量点相对于包络边界无法进一步运动，包容区域处于最小区域，两包络线的间距即为线轮廓度误差。

图5 包容边界达到最小区域Fig.5 The containment boundary reaches the minimum area

4 最小距离求算过程

通过式（1）可求得理想曲线的表达式，对式（3）求一阶导数可得到节点u处的曲线切向矢量：

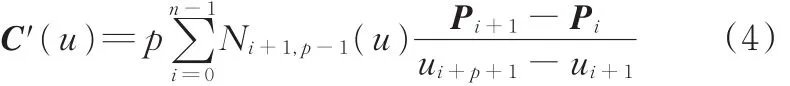
根据直线垂直的特性，可求出对应节点的法向矢量Cn：

基于上述前提与说明，现构造测量点附近平行包络线段，通过寻找线段间最短距离来满足最小区域条件并进行线轮廓度误差求算，具体步骤如下：

（1）假设给定的公差值为a，设计曲线的节点矢量为U，测量点的坐标为Qi（xi，yi），通过式（1）求出设计曲线上点的坐标(,)，k表示设计曲线上的点。对节点矢量U中每一个参数ui计算点距：

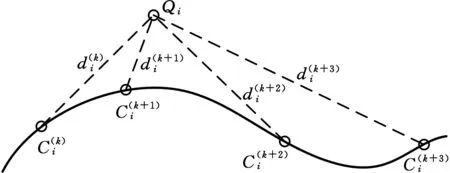
图6 调整理想点与测量点间距Fig.6 Adjusting the distance between ideal points and measuring points

（2）结合式（4）计算各等分点处切向矢量，根据矢量C'(u)与坐标C(k)i(x(k)i,y(k)i)计算切线方程，再由点到直线距离方程，计算各测点Qi与对应切线的距离Di：

式中，A、B、C为切线方程的参数。

找出其中的最大值 Di，max。

通过式（5）求出对应法向矢量Cn（ui），曲线上各点C(k)i沿各自法向矢量方向计算距离为Di，max的新坐标点，且过新坐标点作平行于切线的直线，见图7。此时，Di，max对应的测点已在包络线段上，包络边界L1接触到第一个测点Q1。

图7 构造平行线Fig.7 Tectonic parallel line

（3）当接触第一个测点后，L1沿理想点的反向法向矢量方向向理想曲线靠近，Q1在L1的推动下沿着相同的矢量方向移动。为了保持所有测点的相对位置不变，令所有测点均沿Q1的移动方向改变位置。对于除L1外的其余包络线段，沿各自反向法向矢量方向向理想曲线靠近。在靠近的过程中，所有包络线段的移动速度v均相同。

由于除Q1外其余测点与各自包络线段的移动方向不同，故会出现图8中的三种情况。由于移动速度v相同，因此可能出现离测点较远的包络线段比离测点近的包络线段先接触测点的情况，故此处不能依据距离关系寻找第二接触点Q2。

测点运动方向的方向矢量为Cn（u2），包络线段运动方向的方向矢量为Cn（ui），通过向量夹角公式

图8 向量夹角的三种情况Fig.8 Three cases of vector angle

即可计算出θ：

①θ∈［0o，90o），计算测点到包络线段的距离S，则两者接触时所需时间

②θ=90o，两者接触所需时间

③θ∈（90o，180o］，两者接触所需时间

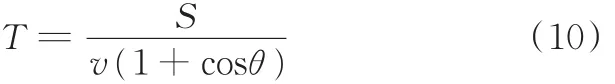
计算出所有时间T后，Tmin对应的测点将作为第二接触点Q2。

（4）找到Q2后，计算Q2接触L2所需的移动距离。以θ∈（90o，180o］为例，构建Q2与L2的几何关系见图9。Q2向A移动，L2向Q2移动，x为Q2和L2的移动距离，h为Q2到A的距离，S为Q2到L2的距离，由相关几何条件可知：

即可求得移动距离x。

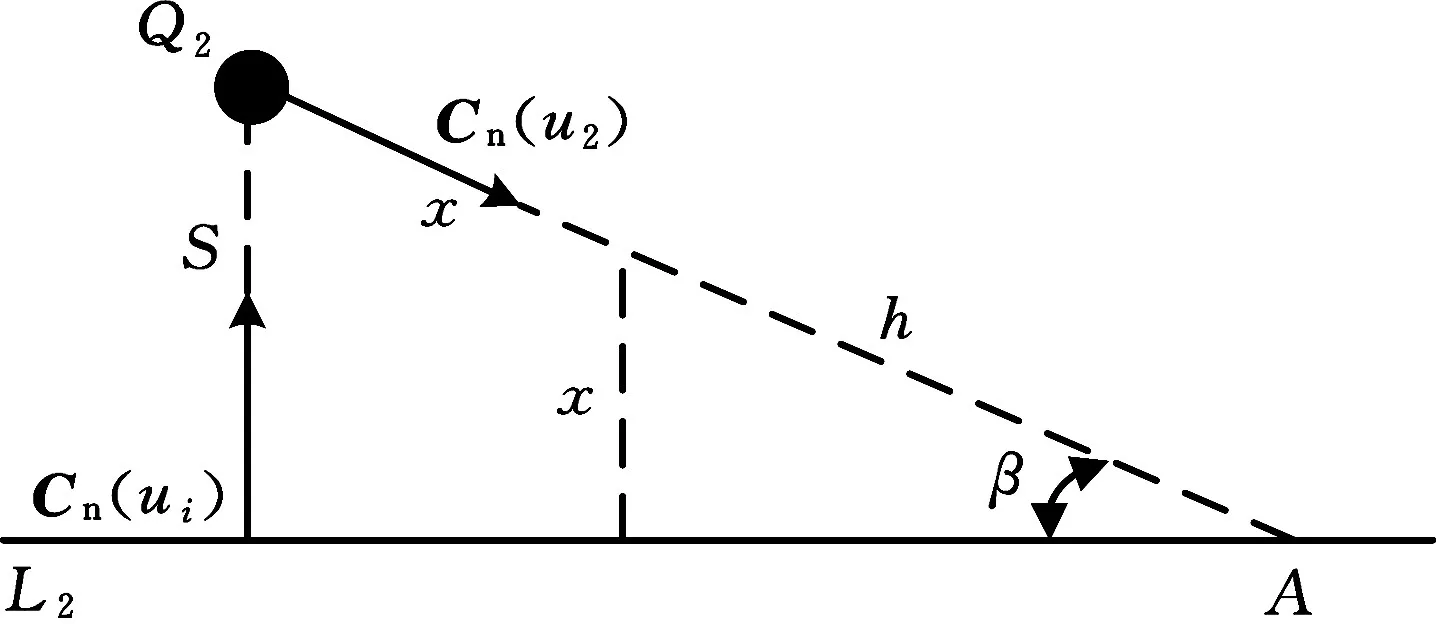
图 9 Q2向L2平移Fig.9 Q2translation to L2

（5）当2个测点均接触到对应包络线段后，第三接触点Q3的搜索是平移和旋转的复合运动。根据国家标准GB/T 1958-2004中关于形状公差及其评定的描述，在最小包容区域的判定中有3种准则，基于此可得到间距最小的两平行平面。同理，在线轮廓度误差评定中可以用此判断最小区域。

Q3的复合运动可将其拆分为平移和旋转2个独立运动依次进行。在Q2接触到L2后，Q1、L1和Q2、L2存在如下2种位置情况（图10）：

①当处于图10a的位置关系时，仍可按照搜索Q2的方式搜索Q3，即只存在平移运动。可以证明，随着L1和L2沿矢量方向平移相同距离后，Q1和Q2能在保持相对间距不变的情况下，平移至处于新位置的两包络线段上，且两点连线与原位置上两点连线平行。

图10 包络线段与测点的2种位置情况Fig.10 Two positions of envelopes and measuring points

②当处于图10b的位置关系时，则会产生旋转运动，旋转中心位于Q1和Q2连线上，见图11。可以证明在Q1和Q2连线上存在一点O使得连线绕O点旋转一定角度α后，其两端点B1、B2与包络线段的间距相等。实际情况下，为满足上述条件，O点会随Q1Q2的旋转而不断改变位置。

图11 旋转运动Fig.11 Rotational motion

设线段Q1Q2长度为L，旋转中心O点将线段Q1Q2分成两部分LQ1O和LQ2O，对应比例关系为

将线段Q1Q2长度代入式（12）中，可得线段LQ1O和LQ2O的长度

根据图11中几何关系，可以证明△OQ1B1∽△OQ2B2。结合式（13），可得线段LQ1B1和LQ2B2长度：

考虑到△OQ1B1和△OQ2B2均为等腰三角形，二者的两底角相等，均为（180°-α）/2，因此两端点B1、B2到包络线段的距离s1、s2分别为

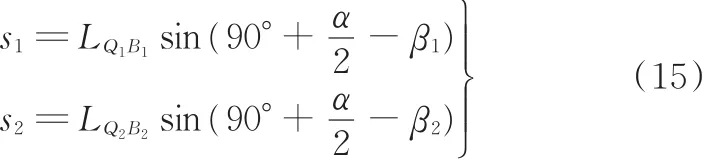
根据s1、s2需相等的条件，可将式（12）化简为

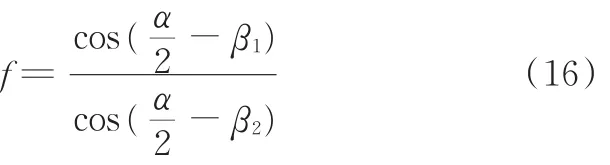
式（16）表明，对于任意α，与β1、β2存在比例p使s1=s2，随着α不断变化，旋转中心O点同时会沿线段Q1Q2移动，当确定一个角度α后可得到唯一对应的p。

此外，在旋转的过程中，β1和β2也会随α发生改变，其与旋转角α的关系为

式中，βp1、βp2分别为转动后β1和β2对应的夹角。

设B（1x1，y1），B（2x2，y2），则转动中心O点（x0，y0）的坐标分量为

（6）线段Q1Q2旋转方向由L1和L2的平移矢量方向决定。分别计算旋转前与旋转后测点到各自包络线段的距离并更新旋转中心点位置。当距离的最小值为0时，Q3接触对应包络线段L3，此时若满足GB/T 11337-2004中的判定要求，则完成最小区域的搜索；若不满足判定要求，则继续旋转直到满足要求。

5 实例分析

本实例利用Hexagon青岛公司生产的三坐标测量机，以接触式测量方法获取零件表面部分区域的测点数据。测量部分为某阶梯轴零件的曲面表面，通过对比仪器自带评定软件与本算法的结果，分析本算法的可行性。表1给出了实际测量点数据。

根据测量数据构造NURBS曲线，设曲线次数p=3，节点矢量 U=（0，0，0，0，0.340 5，0.436 7，0.534 6，0.640 6，0.749 6，0.870 0，1，1，1，1，1），可单独通过改变控制点或权因子来调整曲线形状，因此可设ωi=1。

（1）调整理想点与测点间距。计算表1中的测点与理想点的间距，若理想点与测点的间距大于1.5倍公差值，则在理想曲线上选取新的理想点，最终使理想点与测点的间距小于1.5倍公差值。完成调整后构造理想点处曲线的切线，并计算各测点到对应切线的距离。

表1 被测曲线的实际测点坐标值Tab.1 The coordinate value of the measured points in the measured curve

（2）计算切线方程并搜索最大距离。由理想点的坐标计算得到理想点处的切线方程，再结合测量点数据搜索测点到各自切线的距离Di，其中最大距离 Di，max=0.586 8 mm，对应测点序号为 18，见表2。

表2 理想点到切线距离Tab.2 Distance from ideal point to tangent mm

（3）包络边界接触第一接触点。对所有切线沿各自法向矢量方向，在距离测点0.586 8 mm处构造包络线段。此时第一接触点与对应包络线段接触，且矢量模长均为0.586 8 mm。

（4）搜索第二接触点。根据式（7）计算各测点法向矢量方向与18号测点法向矢量方向的夹角θ，见表3。设所有包络线段沿各自法向矢量方向的移动速度v=1 mm/s，根据θ计算各测点在18号测点法向矢量方向上的分速度，并通过该速度计算测点移动至与对应包络线段接触的过程中，所需时间T的最短时间来确定第二接触点。

（5）搜索第三接触点。由式（11）计算出移动距离x，将测点沿第一接触点法向矢量Cn（u18）方向平移距离D18，包络线段沿各自法向矢量方向平移相同距离，完成第二接触点的接触。

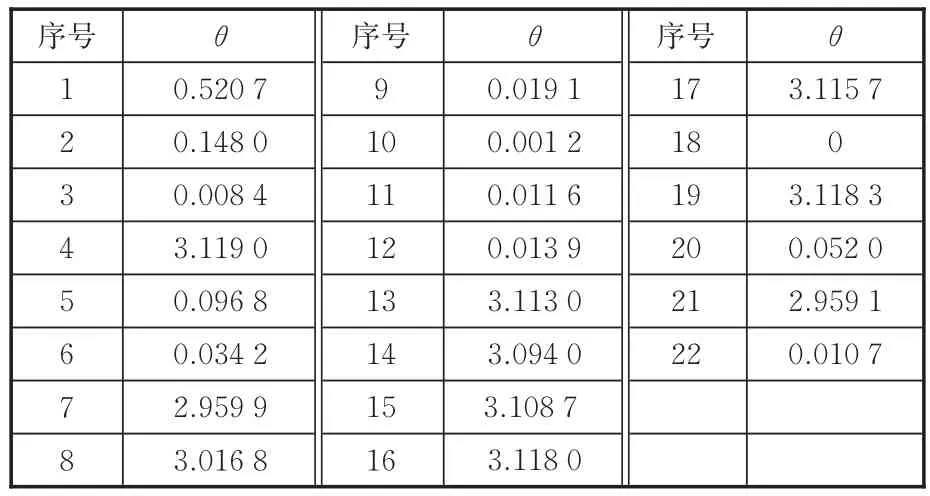
表3 测点矢量与各切线矢量夹角Tab.3 Angle between measuring point vector and tangent vector （°）

此时两个接触点满足图10b中的情况，需通过旋转来搜索第三接触点。反复循环式（12）～式（17）来调整测点位置，并设定s1（或s2）旋转变换前后的误差ε＜0.01时，停止计算。

使用测量仪器自带的线轮廓度误差评定方法所给出的曲线轮廓度误差评定结果为0.484 mm，本文给出算法的评定结果为0.438 2 mm，这表明本算法是有效的，也是正确的。

6 结论

（1）根据轮廓度公差的定义，分析了轮廓度误差的评定过程及相关特征，并建立了模拟实际测量的虚拟量具模型。在遵循物理规律的情况下，模拟实际量具的评定过程，使评定过程中各阶段得到的误差值均比前一阶段误差值小，不存在上下浮动情况，且评定过程中始终考虑所有测量点的整体运动，不存在陷入传统优化算法中局部解的情况，本文方法具有全局性和单一性。

（2）以测量仪器分析数据为对比进行曲线轮廓度误差的评定并给出评定结果，结果表明本算法具备有效性及正确性。

将此方法拓展到复杂曲面的轮廓度误差评定中是今后的工作重点。