一种柔顺微夹钳机构的拓扑优化方法研究
2018-10-22侯晓丹杨鹏飞张学良
侯晓丹,权 诺,杨鹏飞,张学良
(太原科技大学机械工程学院,太原 030024)
柔顺机构是通过自身的部分或全部具有柔性构件的弹性变形来传递力和运动的,具有结构简单、容易装配、容易制造、无摩擦磨损、高精度及高可靠性、轻质量及易实现微型化等优点,已经在航空航天、MEMS(Micro-Electro-Mechanical Systems)器件设计、生物工程显微操作以及光纤对接等领域得到广泛应用[1]。柔顺机构的优越性主要表现在降低成本和提高性能两个方面[2],又因应用前景广泛,所以成为了国内外机构学领域新的热点研究方向。而面向柔顺机构进行拓扑优化具有实用上潜在的极大经济效益,结构拓扑优化一旦能付诸实用,将比结构的截面和形状优化节省更多的结构用材。
A.G.M.Michell 是拓扑优化研究方面的先驱性学者,他得出了最佳单元网,也就是现在著名的 Michell 连续体。Ananthasuresh 等[3]将结构力学上的拓扑优化方法引入到柔顺机构的设计中。张宪民是国内最早提出柔顺机构拓扑优化的学者,在文献[4]中讨论了柔顺机构拓扑优化设计的基础结构法和均匀化方法,并对相关的优化模型、材料模型进行了讨论,进而在文献[5]中对多材料的情况进行了分析。朱本亮[6]对基于水平集法的分布式柔顺机构拓扑优化设计做了深入研究,提出了有效解决类铰链问题以得到分布式柔顺机构的建模方法,同时有效提高了算法的计算效率。
虽然对于拓扑优化的研究已经比较多了,但是有关具体的实现方法,还没有详细的文献进行论述。针对ANSYS软件一般只能进行刚度拓扑优化的问题[7],本文提出基于虚拟载荷方法来实现ANSYS软件对柔顺机构的柔性拓扑优化。同时,本文利用变密度法,建立了以体积为约束、输出位移最大的柔顺机构拓扑优化设计模型;采用优化准则法,在MATLAB软件中实现柔顺机构微夹钳的拓扑优化的一般过程。对虚拟载荷法的拓扑结果进行了静力分析,并与MATLAB得到的结果与进行了比较。
1 虚拟载荷法
图1表示含固定端的一般弹性连续体,输入端作用力为Fin,要求在输出端方向上的输出位移δ最大,也就是机构柔度最大。

图1 虚拟载荷法
Fig.1 The virtual load method
根据文献[8],在力Fin作用下,机构输出端位移δ表达式等效于互应变能(MSE),表示为:

(1)
式中,σd—输出位移方向上仅有一单位虚拟载荷时的应力场;ε—仅有实际载荷作用下的应变场。
同样地,对其离散有限元模型,互应变能为:
MSE={v}T[K]{u}
(2)
式中,{u}—仅有单位虚拟载荷下的位移矢量;{v}—仅有实际载荷下的位移矢量。
2 基于变密度法的柔顺机构拓扑优化模型
一般来说,在进行柔顺机构设计时,之所以能够产生运动,是由于输出端的单点或多点被大量的点所代替了。为了使柔顺机构有足够大的柔性,就要使输出端的位移最大。在力F的作用下,输出端在给定方向上的位移表达式可以用互应变能(MSE)来表示[8]。
(3)
那么,以体积为约束,输出位移最大化的柔顺机构拓扑优化模型可以写成:

(4)
式中,F—输入载荷;U—仅有实际载荷F作用时的位移矢量;ue—计域内任一点在载荷F下的弹性变形;uoutUd—仅有单位虚拟载荷作用时的位移矢量;ud—设计域内任一点在虚拟载荷下的输出位移;K—系统刚度矩阵;k0—单元的刚度矩阵;N—划分单元总数;xj—设计单元的面密度;V0—初始体积;Vj—优化过程中的材料体积。
3 拓扑优化敏度分析
在连续体拓扑优化的最优拓扑结果中,常会出现“空”与“实”单元交错布置的局部区域,也就是所谓的棋盘格现象。针对同一优化问题,随着网格的加密,有时会得到一个完全不同的拓扑结构,这种现象叫做网格依赖性。通过敏度过滤技术,可以消除棋盘格和网格依赖现象。
采用直接法求解结构响应对设计变量的敏度信息,根据式(4),求解目标函数的敏度为:
(5)
由
KU=F
(6)
KUd=Fd
(7)
式(5)、(6)两边同时对设计变量求导可得
(8)
(9)
将式(8)、(9)代入式(5),最终可得目标函数的敏度为:
4 算例
在设计柔顺机构的过程中,最常用到的是伪刚体模型法,然而在设计过程中,往往事先并不知道最终可能出现的结构,而拓扑优化法提供了这样的功能,通过逐步去除材料,最终的材料分布状况即为所得的拓扑结构,不仅不需要从已知的刚性结构出发,而且能带来意想不到的结构。
用典型的柔顺机构——柔顺微夹钳作为求解算例,来详细说明拓扑优化的一般实现方法。在文献[9]中,仅仅分析了柔顺微夹钳输入端受压力的情况,输出位移为0.4 mm;本文采用虚拟位移法,不仅得到了微夹钳输入端受压力时的结果,同时能够得到输入端受拉力时的变形情况;虚拟位移法利用ANSYS和MATLAB得到的输出端位移分别为0.53 mm和1.04 mm,能够实现更大范围内的抓取操作。
图2为微夹钳的设计域,尺寸为80×80,上下两部分关于中心线对称,由虚线将整体划分为A、B、C三个部分,将在MATLAB编程中用到。其他参数如表1.

图2 微夹钳设计域
Fig.2Thedesigndomainofmicro-gripper
表1 微夹钳参数表
Tab.1Micro-gripperparameterslist
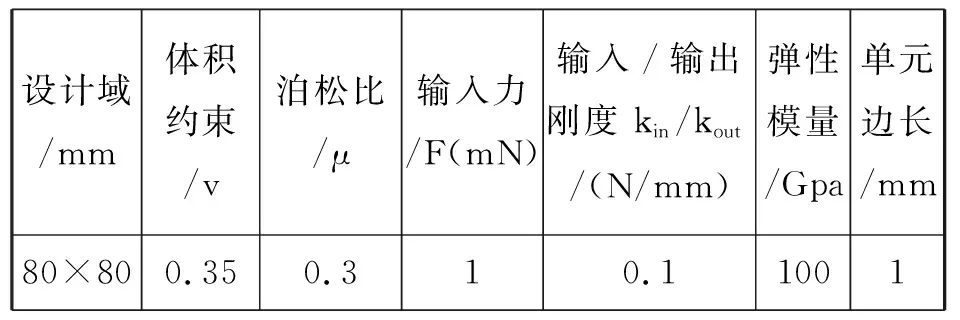
设计域/mm体积约束/v泊松比/μ输入力/F(mN)输入/输出刚度 kin/kout/(N/mm)弹性模量/Gpa单元边长/mm80×800.350.310.11001
4.1 应用虚拟载荷法实现基于ANSYS软件的柔顺微夹钳拓扑优化
基于ANSYS进行柔顺机构拓扑优化属于形状优化,是为了寻找特定载荷下的最佳材料分配方案。
利用Workbench的拓扑优化功能,可以快速得到在承受固定载荷下的结构模型,为后期的详细设计提供依据。
在Workbench的Analysis Systems栏中的Shape Optimization项目模块中进行优化。工作流程为:
(1)设定弹性模量、泊松比;
(2)建立模型;
(3)网格划分;
(4)施加约束和载荷;
(5)指定体积分数,进行求解。
根据公式(3)可知,度量柔性的指标互应变能含有三个量:仅有单位虚拟载荷作用时的位移矢量、刚度以及仅有实际载荷作用时的位移矢量。刚度及实际载荷下的位移矢量是可知的,为得到仅有虚拟载荷作用下的位移矢量,只需要在输出端添加虚拟载荷。
为了与输入载荷相匹配,在输出方向上添加大小1 mN的虚拟载荷。对其进行静力分析之后,得到其拓扑优化结果总变形图(图3),输出端的最大输出位移为0.54 mm.

图3 微夹钳拓扑结果总变形图
Fig.3 The total deformation of micro-gripper's topology result
4.2 基于优化准则法的柔顺微夹钳机构拓扑优化
采用优化准则算法对基于变密度法的柔顺机构拓扑优化模型(3),应用MATLAB编程实现其优化设计。
为避免数值计算不稳定而出现的棋盘格现象,采用SIGMUND等[10]提出的敏度过滤技术来进行过滤,以减少棋盘格现象带来的影响。拓扑优化的最终结果只是优化设计的初级阶段,还需要在三维软件中进行模型的完善,以得到所要求的最终设计。
4.2.1 最优化准则
由于材料体积是单调减少的,故可用一个拉格朗日函数来描述,通过双向切片算法[11]可以得到满足体积约束的拉格朗日乘子。
此处用Bendsoe于1995年提出的算法:
(11)
这里的最小边界条件可以防止相对密度变为0而产生奇异现象,最大边界条件则是要防止密度大于1失去物理意义。
式中,m为移动步长。η是阻尼系数。Be可以由如下条件确定:
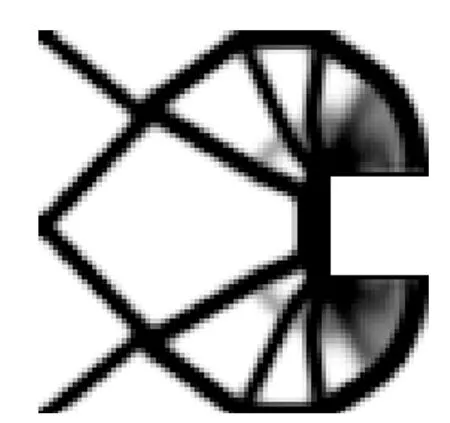
图4 基于MATLAB的微夹钳拓扑结果
Fig.4Micro-gripper topology results based on MATLAB
(12)
λ为拉格朗日乘子,由双向切片法确定。单元敏度即c对x求导,由式(10)可得
(13)
4.2.2 改进的敏度过滤技术
对单元敏度过滤时需要选择过滤半径[12],在达到过滤半径之后,停止过滤。
在更新单元e的敏感度时,需要将半径为rmin范围内的单元进行均匀化处理,可以防止相邻单元敏度变化过大。此处将敏度表达式(10)改进如下
(14)


(15)
式中,dist(e,f)为单元e中心到单元f中心的距离。
4.2.3 结果分析
运行程序,得到基于优化准则法的微夹钳拓扑结果图(图4),之后再做出迭代次数与输出位移的关系图(图5).
由图5可以看出,在第64次迭代之后,达到了目标函数的最优值。此时设计变量的改变量是0.049,达到了收敛条件,目标收敛于-1.04 mm,说明微夹钳位移输出端最大输出位移为1.04 mm,夹钳状态为向内夹紧,拓扑优化后的体积是原设计域的34.7%.
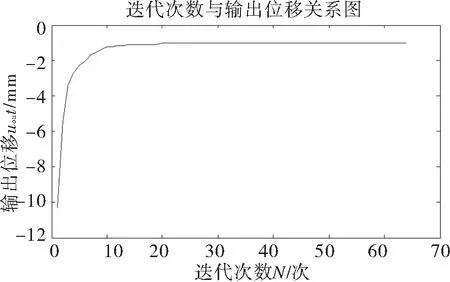
图5 迭代次数与输出位移的关系图
Fig.5 The relationship of iterations and output displacement
与ANSYS得到的结果0.4 mm相比,通过MATLAB编程能够得到更大的输出位移。
5 结论
(1)提出的添加同量级虚拟载荷方法能够解决ANSYS一般只能进行刚度拓扑优化的问题。针对不同的柔顺机构,只要通过设置约束与载荷情况,添加合理的虚拟载荷,就能得到柔度拓扑优化的结果。
(2)针对柔顺微夹钳机构,基于变密度法,在MATLAB中进行编程,得到其拓扑优化结果及位移图。对比结果表明,在MATLAB中利用优化准则法编程得到的输出位移比在ANSYS中得到的大,能够实现更大范围内抓取物品,同时运算速度更快。但是ANSYS的工况设置比较简单,利用MATLAB编程时,设计域的划分及编号,约束条件与载荷设置更为复杂。
